基于变模糊PID控制器的阀控非对称缸复合控制策略
2022-11-16蒲虹云郝兴安邹海锋刘思颂陈清平徐文刚
蒲虹云, 蒋 刚, 郝兴安, 邹海锋, 刘思颂, 陈清平, 徐文刚
(1.成都理工大学 机电工程学院, 四川 成都 610051; 2.成都陵川特种工业有限责任公司, 四川 成都 610100)
引言
非对称液压缸具有工作空间小、承载能力强和结构简单等优点[1],在工业机器人等领域有广泛应用。由于非对称缸正反向特异性差异、外部负载扰动及供油压力变化等因素,电液伺服系统通常具有高度的非线性行为[2]。对电液位置伺服系统,国内外已有许多研究工作,大多工作内容是依据系统特点,应用控制理论成果,结合各种控制策略,提高系统控制精度并改善动态性能。文献[3]通过对称阀控非对称缸的压力特性和输出特性分析,提出阀控非对称缸系统两腔的稳态压力与活塞杆运动方向有关。文献[4]通过建立电液比例阀控非对称液压缸系统的数学模型, 提出液压缸结构不对称性越大,系统的不对称特性越大。文献[5]针对实际电液伺服系统的非线性环节建模不准确的问题,利用AMESim建立复杂系统模型,利用MATLAB/Simulink进行模糊PID控制器设计,提高了系统的鲁棒性和抗干扰性。文献[6]针对直驱式电液伺服系统,采用速度与位置复合控制策略,并针对外负载变化影响液压缸速度的问题,提出带负载力补偿的速度前馈和位置反馈复合控制策略。文献[7]基于比例换向阀设计速度前馈模型,同时设计了模糊PID的压力及位移控制策略,保证试验台对压力、速度的跟踪性能。
针对非对称液压缸正反向运动的不对称性对位移控制精度的影响,设计了根据液压缸运动方向选择对应模糊PID位移控制器的位移闭环控制;为提高系统对速度的跟踪性能,设计了基于伺服阀的速度前馈控制方案;最后,以阀控非对称缸电液位置伺服系统为研究对象,对算法进行联合仿真,验证控制策略对给定位移/速度曲线的跟随效果。
1 系统组成
阀控非对称液压缸位置伺服系统组成如图1所示,系统主要由液压缸的速度位移控制系统和动力系统两部分组成。伺服阀及传感器等构成非对称缸的速度位移控制系统;采用压力传感器实时采集系统油源压力信号及液压缸有杆腔、无杆腔压力信号,计算速度前馈控制信号;通过位移传感器采集活塞杆位移,用于位移闭环控制。速度前馈控制信号与位移闭环控制信号叠加,通过控制伺服阀的阀芯位移来实现对非对称液压缸活塞杆位移的控制。

1.液压泵与电机 2.单向阀 3.液压油箱 4.伺服阀5.有杆腔压力传感器 6.位移传感器 7.负载8.非对称液压缸 9.无杆腔压力传感器10.油源压力传感器 11.溢流阀图1 阀控液压缸位置伺服系统示意图Fig.1 Schematic diagram of valve-controlled hydraulic cylinder position servo system
2 控制策略实现
复合控制策略的基本思想如下:采用速度前馈控制模块,根据期望速度计算非对称液压缸速度控制信号,以控制非对称液压缸按照期望速度快速响应并迅速接近目标位置[8];以期望速度及位移误差为决策条件,判断非对称液压缸运动状态切换模糊PID控制器实现活塞杆位移闭环控制,以提高非对称液压缸位移控制精度。实现上述控制策略的关键技术有:①构造基于伺服阀的前馈控制信号计算模型,实现期望速度信号对应伺服阀控制信号的较精确的计算;②设计选择器,实现位移闭环控制器切换;③分别设计非对称缸正反向运动模糊PID控制器,实现PID参数的在线自调整。基于此提出了变模糊PID控制器的速度前馈及位置反馈模糊控制系统,如图2所示。

图2 速度前馈的位置反馈模糊控制系统Fig.2 Position feedback fuzzy control system with velocity feedforward
在研究中,液压缸无杆腔与伺服阀A口相连。pA表示伺服阀A口处的压力,QA表示通过伺服阀A口的流量;pB为伺服阀B口处压力,pS表示系统油源压力,pL表示负载压力。为方便理解,作如下约定:液压缸活塞杆伸出,速度为正;活塞杆缩回时,速度为负。
阀控液压缸作位置控制输出元件时,弹性负载往往忽略,非对称液压缸力平衡方程为:
(1)
式中,m—— 活塞及负载总质量
B—— 黏性阻尼系数
FL—— 外负载力
A1—— 液压缸无杆腔活塞有效面积
A2—— 液压缸有杆腔活塞有效面积
负载流量连续性方程:

(2)
式中,Cd—— 流量系数
w—— 伺服阀节流口面积梯度
xV—— 伺服阀阀芯位移
Ve—— 速度发生器给定的期望速度
省略中间推导过程,最终可由式(1)、式(2)得到阀控非对称液压缸活塞杆伸出/缩回时的传递函数为:
(3)
式中,Vi—— 等效容积
βe—— 液压介质的容积模数
ωn—— 液压固有频率
ξn—— 液压阻尼比
由于非对称液压缸两腔的非对称性,活塞杆正/反向运动时系统的开环增益、固有频率、阻尼比等参数均发生了变化,使得非对称液压缸在正/反方向上的超调量、上升时间和稳态误差也均存在非对称性[9]。针对这一现象,采用固定参数PID控制及传统的不区分阀控非对称液压缸运动状态的模糊PID控制策略,效果均差强人意[10]。因此根据阀控非对称液压缸活塞正向及反向运动状态分别设计模糊PID控制器,并通过模糊控制器选择器实现在控制过程中控制器的切换。
2.1 速度前馈计算模型
忽略非对称缸内泄漏的情况,推导基于伺服阀控制非对称液压缸的前馈量计算模型。
液压缸无杆腔和有杆腔的有效面积关系可表示为:
(4)
式中,D—— 液压缸缸径
d—— 活塞杆杆径
计算前馈控制量所需的无杆腔压力可由下式计算得出:
(5)
有杆腔压力可由下式计算得出:
(6)
伺服阀输出流量与压降的关系[11]为:
(7)
式中,y—— 伺服阀输入信号
ymax—— 伺服阀最大开口时输入信号
ΔpN—— 伺服阀控制信号100%时的单边压差
QN—— 伺服阀在单边额定压差ΔpN时的额定流量[11]
非对称液压缸无杆腔流量和活塞杆的速度V关系为:
q1=VA1
(8)
将式(2)和式(3)带入式(4)整理并进行单位化简,可得伺服阀控制非对称缸活塞杆正向/反向运动时的速度前馈控制信号计算公式:
(9)
速度前馈控制信号计算模型中包含了负载、速度的信息,在给定的不同期望速度和负载变化,得到对应速度前馈控制信号。
2.2 选择器设计
以位移跟踪误差e及期望速度信号Ve为决策条件,设计模糊PID控制器选择器。期望速度为正,位移跟踪误差为负,采用模糊PID控制器1;期望速度及位移跟踪误差同号,采用模糊PID控制器2,如图3所示。
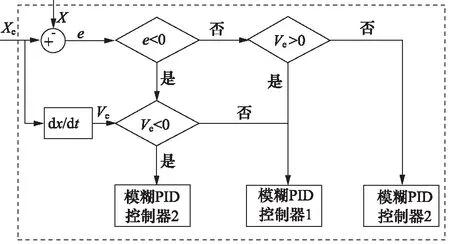
图3 模糊PID控制器选择流程图Fig.3 Flow chart of fuzzy PID controller selection
2.3 模糊自适应PID控制器设计
针对非对称液压缸正反向运动的不对称性和负载变化对位移控制精度的影响,因此针对非对称缸正/反向设置不同论域的两种的模糊PID控制器。在研究中发现采用一种模糊控制器被测缸反向较正向运动位移跟踪误差更大,以非对称缸反向运动为例设计模糊PID控制器。

将输入变量、输出变量的论域划分为7个模糊子集:PB(正大)、PM(正中)、PS(正小)、Z0(零)、NS(负小)、NM(负中)、NB(负大),确定隶属度函数的形式为三角形。
综上,分别建立非对称缸反向运动kp,ki,kd模糊控制规则如表1所示。
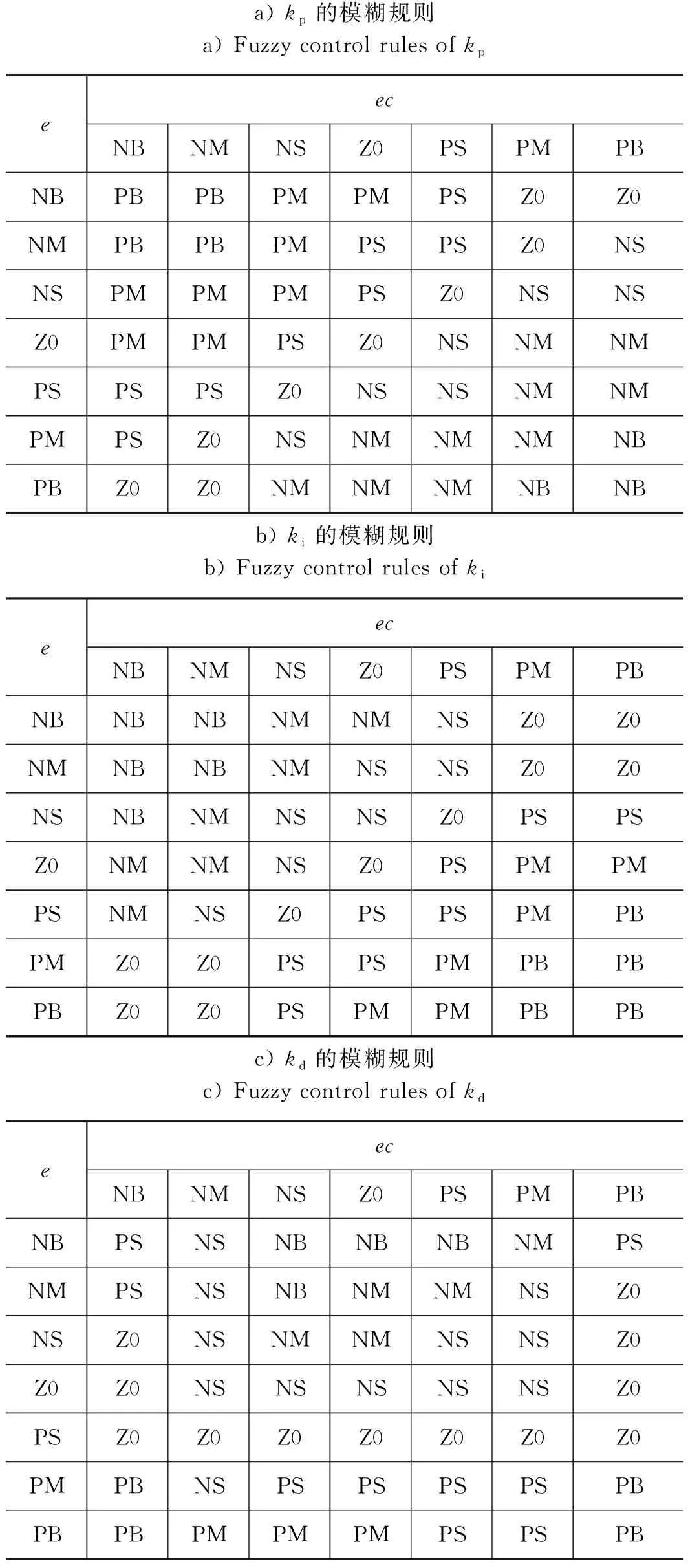
表1 模糊PID模糊控制规则Tab.1 Fuzzy PID fuzzy control rules
然后,经过输入模糊化、模糊推理、解模糊等过程,得到3个输出变量的大小,如式(7),实现PID参数在线调整[13]:
(10)
式中,kp,ki,kd—— 经过修改后的PID参数
kp1,ki1,kd1—— 参数修改值
如式(8),模糊PID控制器处理不同的e及ec所构成不同组合,Δkp,Δki,Δkd作为模糊控制器对PID参数的修改值得到需要的输出量U,都存在不同的U与之对应[14]:
(11)
3 系统的建模与仿真
3.1 阀控缸动力学模型建立
本研究的阀控非对称液压缸伺服系统基于一款六足液压机器人。如图4所示,以机器人左侧前腿的支撑项为例。在软件CREO中建立六足机器人的三维实体图,将其导入ADAMS环境中,并按需求设置仿真参数。
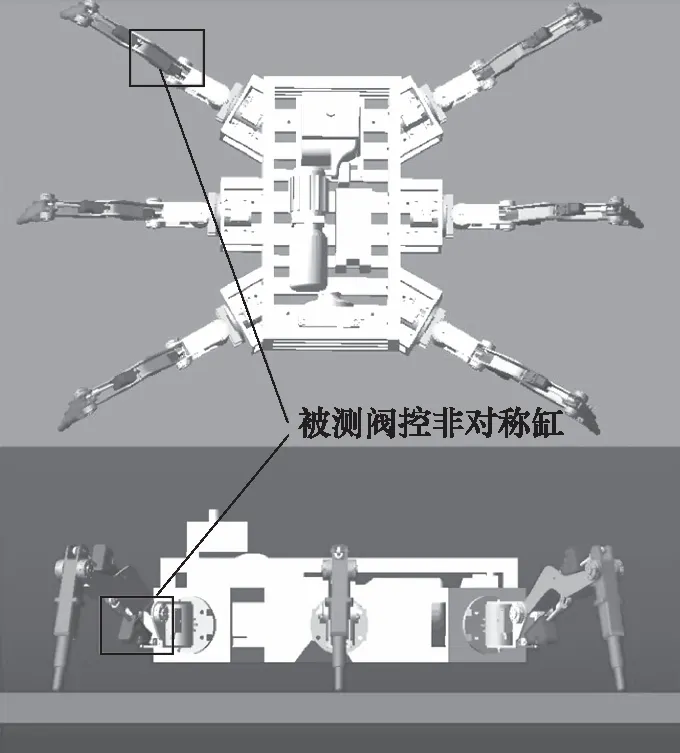
图4 足式机器人ADAMS仿真Fig.4 ADAMS simulation of foot-type robot
当六足机器人采用四足步态,设置仿真时长为8 s,间隔0.01 s,足式机器人完成行走,腹部贴地的动作,得到液压缸活塞杆相对缸体的位移和速度曲线,如图5所示。由于六足机器人存在初始站立姿态,位于该支撑项的液压缸活塞杆相对缸体存在0.026 m的初始位移。

图5 期望速度和期望位移信号Fig.5 Desired velocity and displacement signals
采用ADAMS中的Controls模块,将仿真得到的位移Xe作为输出信号,并生成ADAMS于AMESim的联合仿真模块[15]。更改仿真参数及对象,可得到机器人任一非对称液压缸执行器的速度及位移信号,分别作为速度前馈控制的期望速度信号及位移闭环的期望位移信号。
3.2 AMESim联合仿真模型搭建
电液位置伺服系统属于非线性系统,在实际研究中难以构建全面的数学模型,因此采用AMESim,ADAMS和Simulink联合仿真。通过Simulink中的S-Fuction模块搭建速度前馈计算模型、模糊PID控制器选择器模块、模糊PID控制模型等,通过调用语法实现MATLAB/Simulink与AMESim求解器交互[16];再根据阀控非对称液压缸位置伺服系统原理图与系统控制框图,结合AMESim中的库元件、ADAMS与AMESim联合仿真模块(联合仿真模块1)、AMESim与MATLAB/Simulink联合仿真模块(联合仿真模块2)搭建阀控非对称液压缸变模糊PID控制器的位移控制系统联合仿真模型,如图6所示。
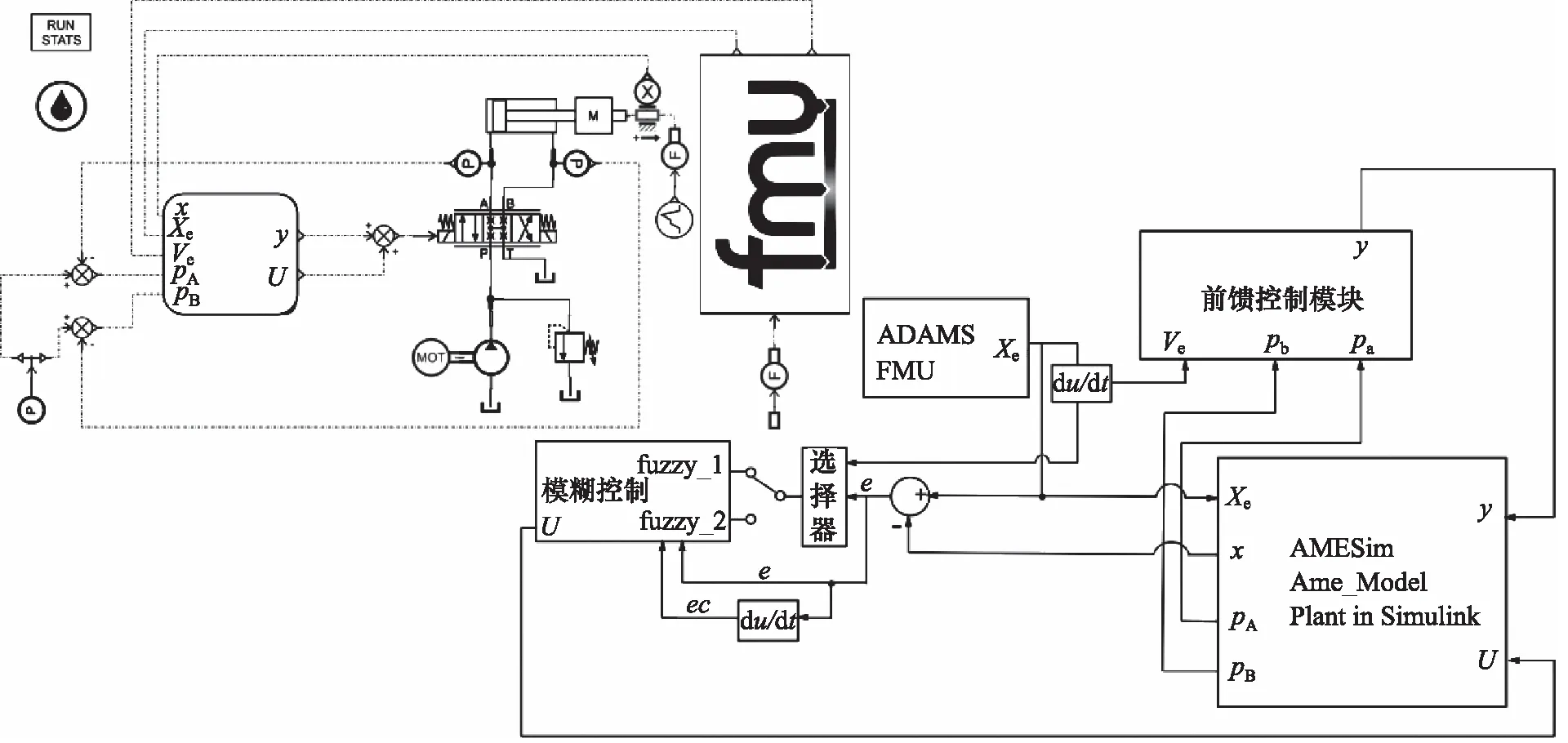
图6 AMESim联合仿真模型Fig.6 AMESim co-simulation model
采集被测缸A/B口压力、系统油源压力和位移信号,与联合仿真模块1的输出信号Ve,Xe在联合仿真模块2中实现速度前馈控制及位移闭环控制。作为对比的传统模糊PID控制其参数设置及模糊规则均与模糊PID控制器1完全一致,液压系统仿真主要参数见表2。

表2 系统构建参数Tab.2 System construction parameters
3.3 仿真结果与分析
为便于观测上述控制策略效果,做了以下工作:首先根据经验设置PID控制器的初始值,再根据位移误差及其变化率定义模糊控制规则[1],设计了传统模糊PID控制器1(控制器1);阀控非对称缸活塞杆正向运动采用与控制器1相同模糊规则,而针对活塞杆反向运动时位移误差e及其变化率ec设计了模糊PID控制器2(控制器2),得到不同控制策略下被测液压缸的位移跟踪曲线,如图7所示。

图7 非对称缸位移跟踪曲线Fig.7 Displacement tracking curve of differential cylinder
从图7可以看出,采用速度前馈 - 模糊PID控制策略的阀控非对称液压缸换向位移误差控制在0.42 mm以内,传统PID控制方法换向时位移误差为1.12 mm,而采用前馈 - 变模糊PID控制器控制策略位移误差减小至0.18 mm。
从图8a中可以看出,由于上述策略中只针对被测缸反向运动设计了控制器2, 而正向运动仍采用控制器1,因此两种策略被测缸正向位移曲线基本重合;从图8b可以看出,采用改进策略后非对称缸的反向运动最大位移跟踪误差减小0.82 mm。

图8 不同控制方法的位置跟踪误差Fig.8 Position tracking errors of different control methods
从图9、图10中可以看出,采用基于速度前馈的模糊PID控制策略,阀控非对称缸在定负载及变负载情况下,可有效控制活塞杆的运动速度。从图10、图11中可以看出,阀控非对称缸在定负载条件下,采用基于速度前馈的变模糊PID控制器控制策略,阀控非对称缸快速跟踪期望速度且可提高速度的控制精度。
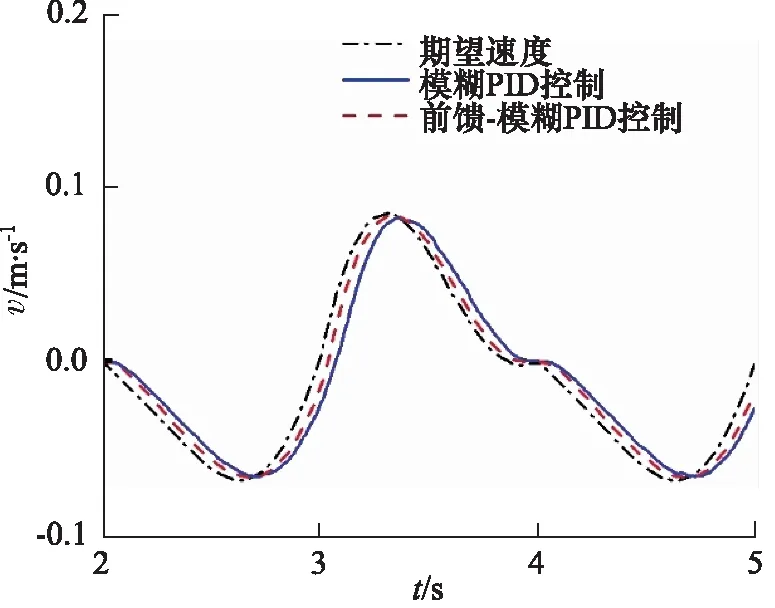
图9 测试缸变负载速度曲线Fig.9 Variable load velocity curve of test cylinder

图10 测试缸定负载速度曲线Fig.10 Test cylinder constant load velocity curve

图11 变模糊PID控制器控制速度仿真结果Fig.11 Simulation results of variable fuzzy PID controller control speed
4 结论
(1) 基于ADAMS的动力学仿真,可方便得到六足机器人各非对称液压缸执行器期望位移/速度曲线;基于AMESim元件库搭建液压仿真回路,同时基于Simulink对控制策略实现。通过联合仿真方式,提高了控制策略验证效率;
(2) 通过联合仿真研究表明,采用复合控制策略的非对称缸在定负载及变负载情况下,系统响应更快;
(3) 采用基于速度前馈的变模糊PID控制器控制策略,提高阀控非对称液压缸速度跟踪响应的同时,减小执行器换向时的位移误差;采用变模糊PID控制器控制策略可提高非对称缸对期望位移曲线的跟踪精度,从而提高机器人足端的位置控制精度。
