基于差分-变分模态分解与全局信息分析网络的辐射源个体识别方法

韦建宇 彭来献 俞璐 王华力 曾维军

（中国人民解放军陆军工程大学通信工程学院，江苏南京 210007）

1 引言

通信辐射源个体识别（SEI，special emitter identification）技术可以根据不同的发射器的指纹特征来识别通信无线发射器［1］。指纹特征是发射器中单个硬件固有差异的结果，主要是由于硬件在制造过程中的不完善导致的［2］。每个发射器的指纹都是独一无二的，很难被伪造，因此SEI技术在军事和民用领域具有重要的研究价值。近几年来，随着自组织网［3］、物联网［4］、认知无线电［5］和无人机通信的快速发展，电磁环境已经变得非常复杂［6］。由于动态电磁频谱共享技术的运用，电磁空间中无线通信安全已经成为一个迫切需要解决的问题。物理层安全机制的研究是解决无线通信安全问题的根源所在，信号的指纹特征是独一无二并且难以被伪造的，因此通信辐射识别技术可以识别复杂电磁空间中的通信无线电发射器的个体信息，它不仅有利于解决通信中的恶意攻击问题，而且对电磁空间的大数据分析和信息挖掘也有着很大的意义。

特征提取是通信辐射源识别技术的重要阶段。根据前人研究，指纹特征提取方法可以分为基于专家经验的传统特征提取方法和基于深度学习的特征提取方法。传统方法研究时间较长，人们采用多种信号处理的方法对信号的不同域进行特征提取。文献［7］提出一种基于Wiger 和Choi-Williams 的辐射源指纹提取方法，该算法能够在同一类型的通信辐射源识别中达到98%的识别率。文献［8］和［9］使用传统的模态分解方法得到希尔伯特谱，并对其提取均值、方差和能量熵特征组成的特征向量作为辐射源的指纹，在5 分类同型号的辐射源识别中取得96%的识别效果。然而这些信号特征只是对信号某些特定方面的分析，并且在经验模态分解（EMD，empirical mode decomposition）过程中存在模态混叠等分解不充分的影响，因此其在低信噪比下识别效果较差。随着深度学习的发展，近年来人们致力于使用信号处理与深度学习相结合的方法去解决辐射源个体识别问题。文献［10］提出将信号的压缩双谱图与卷积神经网络（CNN，convolutional neural network）相结合，在5 分类不同型号的通用软件无线电外设（USRP，universal software radio peripheral）实测数据上略显成效；文献［11］使用信号的差分星座轨迹图作为网络的输入，在30 dB 情况下对54个ZigBee 设备的识别率能够高达99.1%；文献［12］使用EMD方法对信号进行分解，并且通过希尔伯特变换（HHT，Hilbert transform）得到希尔伯特谱，将希尔伯特谱输入到深度残差网络中，通过仿真实验验证了方法对噪声具有较强的鲁棒性。

传统方法主要存在特征提取不全面和泛化能力差的问题。为了更好地提取信号中的指纹特征，人们倾向于使用信号处理与深度学习模型相结合的方法，由于网络模型是自动提取信号的特征进行分类任务，因此经过信号处理以后，输入信号的完整性以及输入数据是否适合网络模型训练是取得良好识别效果的关键。基于以上分析，本文提出了一个将深度学习和信号处理相结合的新型通信辐射源个体识别方法。本文对接收信号进行差分处理，通过建模可以发现，差分信号能够保留并放大信号本身的增益不平衡、直流偏置和载频偏移等指纹特征［13］，为了更好的表现出差分信号的优势，本文采用信号处理的方法对信号进行分解，针对EMD分解不充分的缺点，本文采用变分模态分解（VMD，Variational Mode Decomposition）对差分信号进行分解得到希尔伯特谱，可以有效地表现出信号指纹特征在低频段的分布；针对希尔伯特谱的稀疏特性，本文在CNN 的基础上添加改进的全局信息分析模块，对希尔伯特谱进行全局细微特征的提取，通过对照实验来测试提出方法的性能。

2 基于差分-变分模态分解与全局信息分析的算法

本文算法流程如图1所示，首先对信号进行差分处理，采用VMD方法分解差分信号并转换成希尔伯特谱；然后针对希尔伯特谱的稀疏特征，本文在CNN中添加改进的全局信息分析模块对其进行深度特征的提取，最终对不同的通信辐射源个体进行识别。

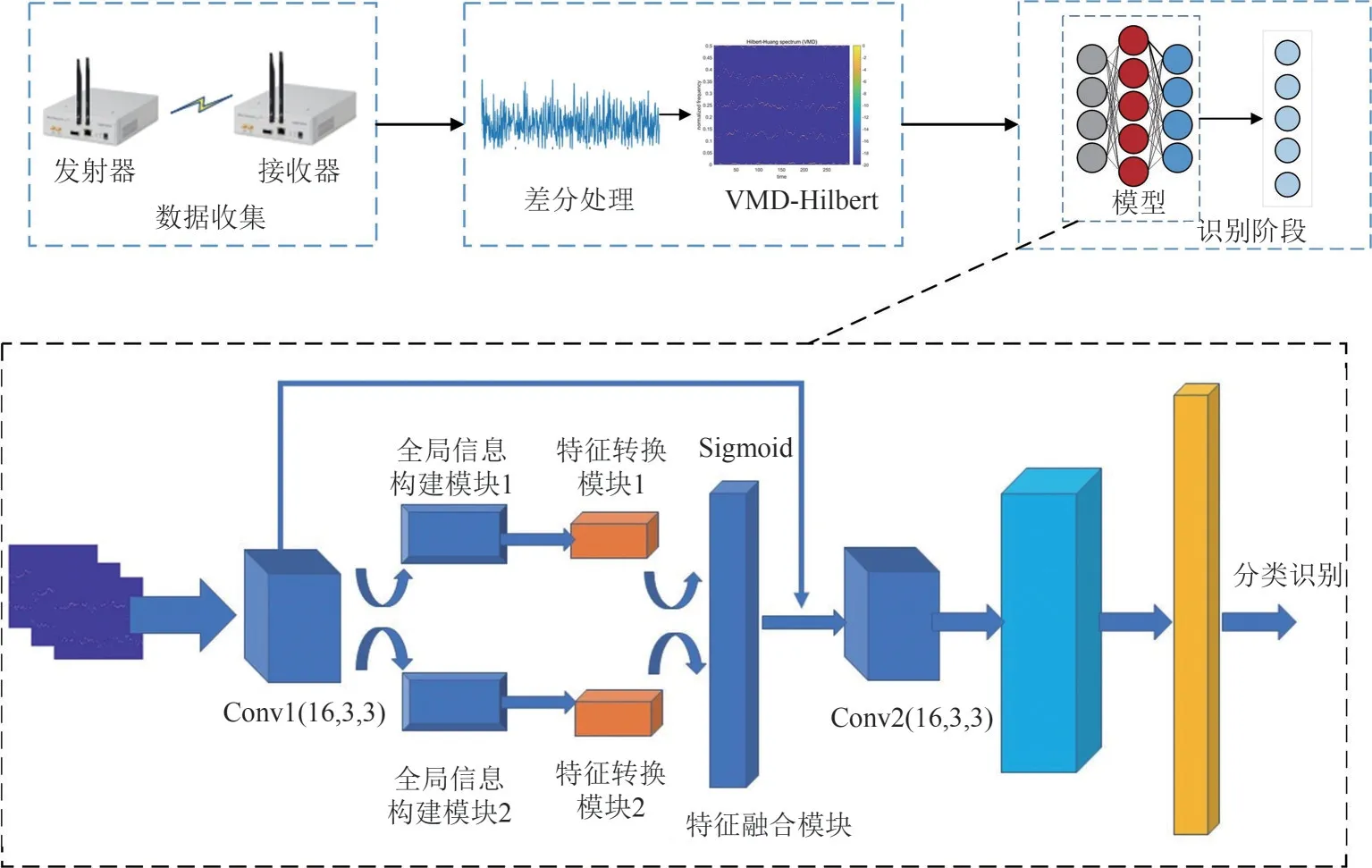
图1 本文算法的流程图和网络结构图Fig.1 The process for the proposed method and the structure of the Network model

2.1 差分信号的处理

本文使用希尔伯特谱作为网络的输入样本，它是对差分信号进行VMD-Hilbert 变换得到的，包含大部分的信号指纹信息，接下来对它进行理论上的分析。发射端的发射信号为：

其中，xI(t)和xQ(t)是发射的I 路信号和Q 路信号，fc1是发射机的载频，αI和αQ是I/Q 信道中的直流偏置，βI和βQ是I/Q 增益不平衡。我们假定信道是理想的，并且使用同一台接收机接收信号，接收的信号可以被转换成：

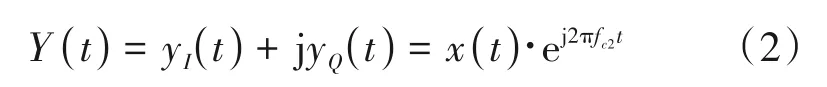
其中，yI(t)和yQ(t)是接收的基带I 路信号和Q 路信号，fc2是接收机的载频。由于生产过程的技术偏差产生了载频的偏移，ψ=fc2-fc1。对信号进行差分处理时不需要频率和时间同步，可以表示为：

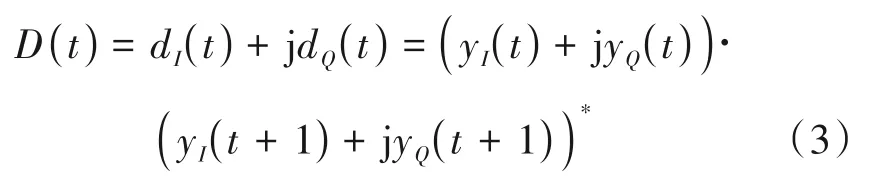
其中，dI(t)和dQ(t)是I 路和Q 路的差分信号，(·)*是共轭运算。将公式（1）、（2）代入公式（3），差分信号最终被写成：

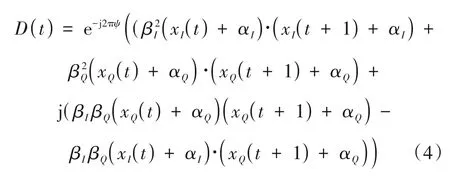
为了便于实验研究，采用xI(t) ≈xI(t+1)和xQ(t) ≈xQ(t+1)的情况，其差分信号可以化简为：

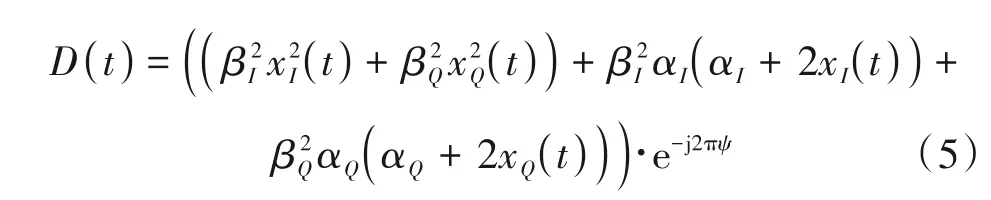
在公式（5）中，αI和αQ远远小于信号xI(t)和xQ(t)，因此项放大了I/Q 信号增益不平衡的指纹特征，公式也包含了直流偏置αI和αQ以及载频偏移ψ这些指纹特征。为了更加直观的反映这些指纹信息，我们将对差分信号进行VMD-Hilbert 变换处理得到对应的希尔伯特谱。在常用的EMD 方法中，其分解的IMF存在严重的模态混叠和端点效应问题［14］，因此影响着希尔伯特谱中的能量分布，而本文采用VMD 分解信号，大大改善了模态的频谱混叠问题。VMD 是一种处理非线性和非平稳信号的有效方法，具体步骤见文献［15］，由于VMD算法中使用内嵌式维纳滤波器，其分解过程对高斯噪声有较强的鲁棒性。因此VMD 算法不仅能够缓解模态混叠现象，而且能够降低外界噪声带来的干扰。我们表示信号为：

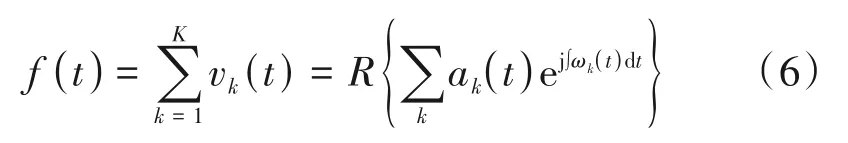
其中f(t)代表待分解的信号，vk(t)代表经过VMD分解后第k个模态分量，代表信号的 瞬时幅 度，是vk(t) 的希尔 伯特变换，代表信号的瞬时相位，θk(t)=以上公式使我们能够将ak(t)和ωk(t)表示为三维图中时间的函数，幅度-时间-频率的三维分布图被指定为希尔伯特谱Hk(ω，t)。

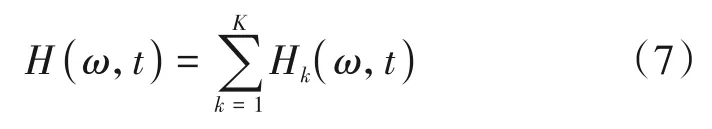
其中，Hk(ω，t)是第k个模态的希尔伯特谱，H(ω，t)是原信号的希尔伯特谱。

希尔伯特谱是一种常见的时频分析方法，首先，VMD 能够根据信号自身的特点分解信号，与使用固定的基函数的传统分析方法相比更加具有普遍性。其次，希尔伯特谱中首次提出了瞬时频率的概念［15］，在信号分析时，该方法强调信号的瞬时特征分析，因此更加有利于捕捉信号指纹特征的瞬态变化。最后，由图2～图3可知差分信号通过VMD分解后得到的希尔伯特谱能够更加清晰地反映出其低频分量随时间的变化，原信号的增益不平衡、直流偏置以及载频频偏等低频段指纹信息变得更加明显，并且在VMD 分解过程中信号没有丢失原有的信息，因此差分信号经过VMD-Hilbert 变换得到的希尔伯特谱能够在时频域内反映出信号的指纹信息。

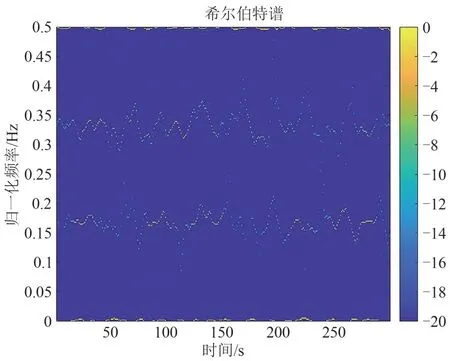
图2 I/Q包络信号的VMD-Hilbert谱Fig.2 The Hilbert spectrum obtained by I/Q signal

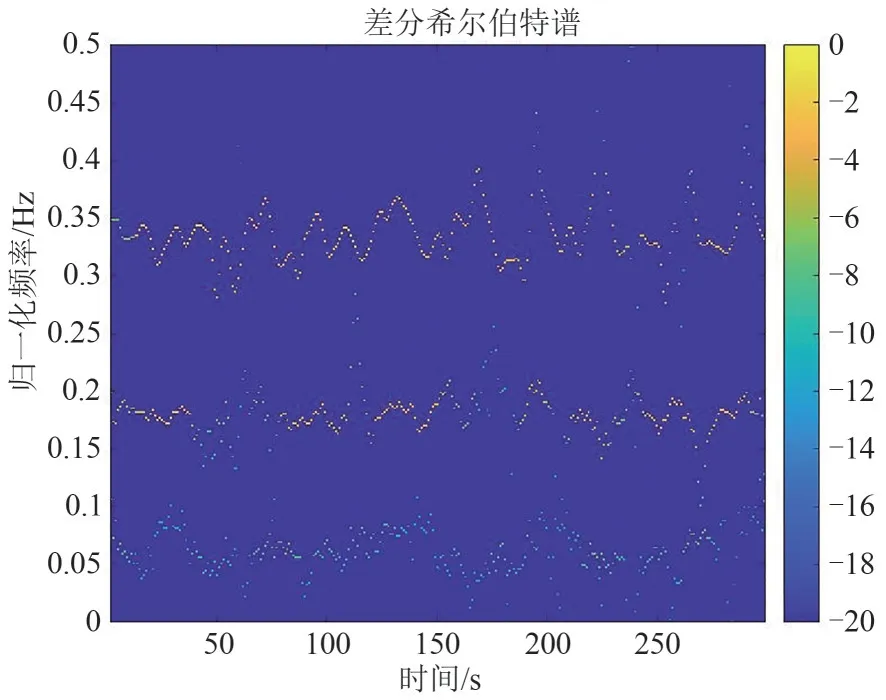
图3 I/Q差分信号的VMD-Hilbert谱Fig.3 The Hilbert spectrum obtained by differential signal

2.2 网络模型架构

在CNN 的模型中，卷积层在特征图的局部区域建立点与点之间的关系，而远距离的点只能通过堆叠多个卷积层来进行建模，然而，这种方法增加了模型的计算复杂度。希尔伯特频谱中的能量分布是稀疏的，在实际信道中存在大量的噪声，使得网络的卷积层注重提取信号和噪声之间的短程相关特性，忽略了信号本身全局相关特性。本文使用全局信息构建［16］的思想对CNN 进行改进，它结合了非局部模块（NL net，non-local network）［17］和挤压激励模块（SE net，squeeze and excitation network）［18］，该模块主要分为三个步骤：全局信息构建阶段、特征转换阶段和特征融合阶段，具体结构如图4 所示。该网络的信息分析模块借鉴了NL net，采用自注意力机制来建模各像素对之间的远程依赖关系。建模远程依赖旨在加强学习过程中对接收信号信息的全局理解，在卷积神经网络中，卷积层主要作用与局部区域，由此远程依赖仅能通过堆叠多层卷积层进行建模，但是多个卷积层的堆叠不仅计算量大，而且难以优化。为了解决此问题，NL net 采用自注意力机制来建模远程依赖，对每个像素点首先计算查询点与所有点之间的成对关系以得到注意力图，然后通过加权和的方式聚合所有点的特征，从而得到与此查询点相关的全局特征，其原理可参考文献［17］，简化结构如图4 全局信息构建模块所示。由于SE net 具有轻量级的特点，能够减少大量的计算量，并且提取出更加有用的信息，特征转换模块引用了SE net的思想，因此，GC net 网络既能够像NL net 一样有效的对全局特征进行提取，又能像SE net一样具有轻量级特性。此网络能够弥补CNN 的局部感受野的缺陷，对输入的数据进行全局特征的有效提取。

在全局信息构建模块中，根据文献［17］的NL net，全局相关的特征是相互独立，与查询位置无关，因此我们可以通过将特征图f(xi，xj)对应的全局特征点从HW×HW变成HW× 1 × 1，其输出从C×H×W变成C× 1 × 1。因为C× 1 × 1 蕴含了各通道中各位置的信息，所以用它来代表每个通道构建的全局信息。f(xi，xj)表示位置xi和xj之间的特征关系图，H和W代表特征图的长和宽，C代表模型的通道数，加号代表各项求和，乘号代表矩阵的内积。根据文献［16］，该模块的输出z为：

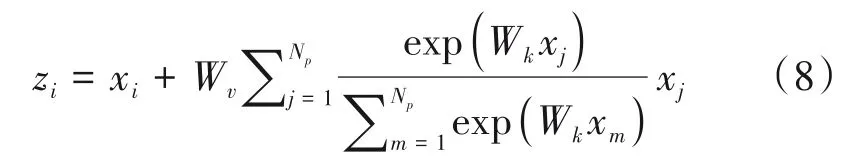
其中xi代表输入模型数据的第i个位置，zi代表输出模型数据的第i给位置，Np=H×W代表特征图的大小，Wk是卷积层Conv(1 × 1)的参数矩阵。

在特征转换模块中，数据经过NL 模块后，由于Conv(1 × 1)的参数是C2，即随着通道的增加存在着参数量较大的问题。根据文献［18］，SE模块有着参数轻量级的特点。因此本文使用SE 模块代替Conv(1 × 1)层，使得参数量从C2减少到2C×C/τ，其中τ是瓶颈比率，C/τ表示瓶颈的隐藏表示维度。由于两层的SE变换增加了优化难度，因此在过程中加入归一化层可以减少优化难度。最后的全局相关信息模块（GC block，global context block）结构如图4所示。

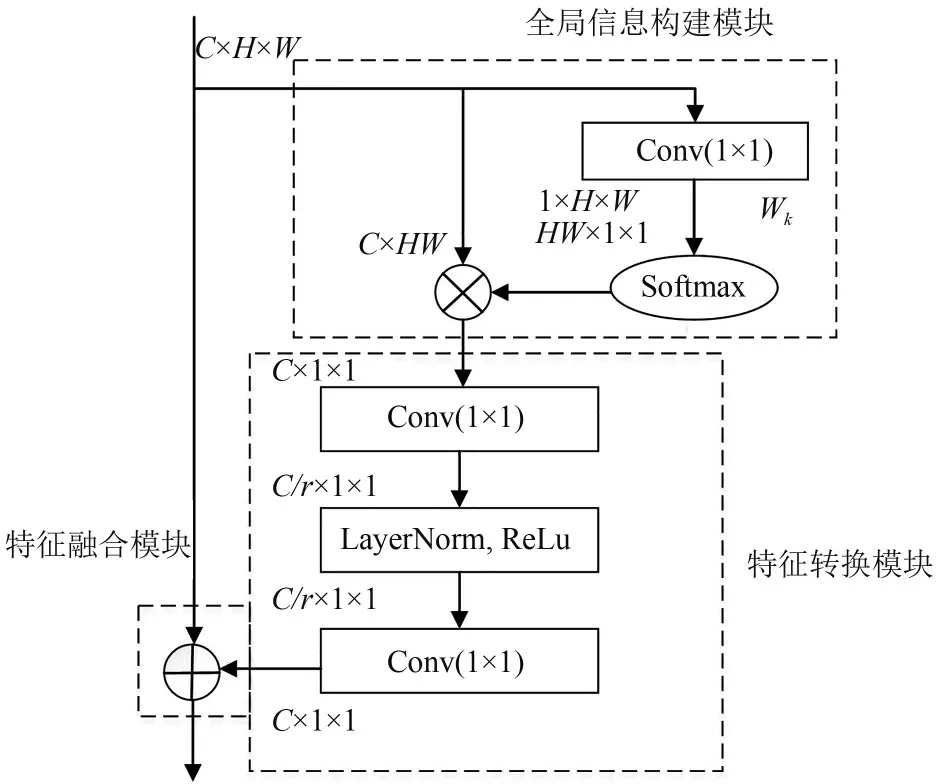
图4 经典全局信息分析模型Fig.4 The classical global context model

上述分析GC 模块能够捕捉到输入数据的全局信息。然而此模型仅仅针对每个通道的特征图进行全局信息的构建，并且将结果与原始数据进行简单相加。它忽略了每个通道相同位置之间的相互关系。这些位置是因为不同的卷积核得到的不同结果，不同的卷积核将原始特征图的相同位置映射到不同的通道中，因此每个通道对应位置的相互关系可以通过建立通道之间的全局信息来捕获。本文在GC 模型的基础上，借鉴双注意力机制的思想，用Sigmoid 函数处理输出结果，将其映射到0 和1 之间，对应的数值不仅蕴含着通道和对应位置的全局信息，而且能够表示不同通道和位置的重要程度。本文将该模块的输出与原始数据对应相乘，使得数据完成全局信息的构建以及各部分重要性的重新分配。改进后的全局信息分析模块如图5所示。

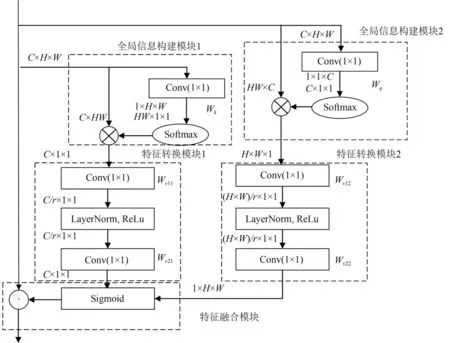
图5 改进的全局信息分析模型Fig.5 The improved global context model

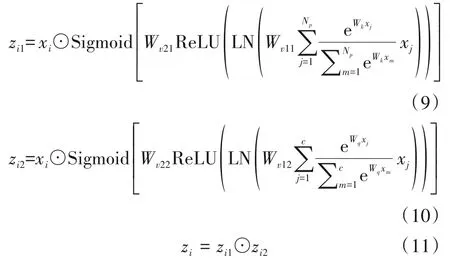
其中，点积运算⊙表示矩阵对应元素相乘，x=是模型输入数据，是模型输出数据，LN表示LayerNorm层，Wk、Wq、Wv11、Wv12、Wv21、Wv22表示对应的Conv(1 × 1)的参数。

本节针对希尔伯特谱的稀疏性和实际噪声的干扰提出了改进的GC 模块来深入提取希尔伯特谱中的细微特征。该模块简单易懂，可以插入到任何普通的神经网络中。CNN 在处理图像数据方面有明显的优势，因此本文将上述模块加入到CNN 网络中。

3 实验结果与分析

3.1 数据集建立

为了提高实验结果的可信度与方便人们接下来的研究，本文使用ORACLE［19］数据集。该数据集记录了大量位相似通信发射器的IQ数据样本，即相同的硬件、协议、物理地址和介质访问控制地址。在ORACLE 中，使用相同型号的USRP 作为发射器，并且使用同一个接收机对信号进行接收操作。本文IQ信号转换为时域包络信号：

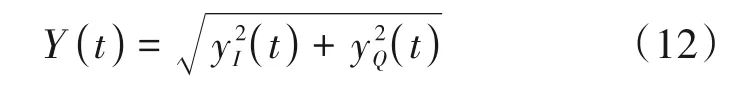
其中，yI(t)和yQ(t)分别代表接收的I 路信号和Q 路信号，Y(t)代表时域包络信号。本实验使用固定的USRP B210 作为接收机，使用多台同型号USRP X310 作为发射器。首先发射端收到由MATLAB WLAN 系统工具箱生成的符合IEEE 802.11a的标准帧，然后将这些帧通过无线信道传送到接收端，其载频为2.45 GHz，最后接收机采用5 MS/s 的采样率对信号进行采样。该实验为每个USRP 发射器收集了2000 万个IQ 点，发射器与接收器之间的距离从2 英尺增加到62 英尺，间隔为6 英尺。本文选择距离为62 英尺的7 分类数据集进行实验，该实验以300 个IQ 点为样本，每个发射器有1000 个样本，最终每个样本经过预处理操作转换为300×300的希尔伯特谱，数据集按照6∶2∶2的比例分为训练集、验证集和测试集，样本大小的选择见3.3节。

3.2 算法复杂度分析

本文对数据预处理过程和网络离线训练过程的复杂度进行了重点比较分析。在数据预处理阶段，重点是模态分解方法的复杂度，本文算法使用VMD 对信号进行分解，其使用变分方法对模态进行迭代计算，为了比较EMD 和VMD 的计算复杂度，在同一台计算机上并且数据相同的情况下，本文对EMD-EM2［13］算法和VMD-EM2［14］算法进行计算时间的分析。这些模拟是在配置MATLAB R2019、i7 处理器、2GB 随机访问存储器（RAM，Random Access Memory）的计算机上进行的，其计算结果如表1 所示。在通信辐射源个数增加的情况下，VMD 算法的计算时间相较于EMD 算法有着较大的提升，所以VMD 方法大大降低了数据预处理部分的计算复杂度，优化了算法的性能。在网络模型离线训练阶段，卷积层是模型特征提取的关键部分，我们对卷积层的个数进行研究。在图6 中，L1 代表卷积层，L2代表全局信息构建模块，L3代表全连接层。为了探究合适的网络结构，本文分别使用5 个模型进行实验，模型的每秒浮点运算次数（FLOPS，floatingpoint operations per second）和准确率如表2 所示。由Model2 和Model3 的对比可知，全局信息构建模块应该设立在前端的卷积层之后比较合适，因为随着卷积层数的增加，图片的局部特征被充分提取，一定程度上破坏了原图中的全局信息，使得全局特征的提取效果变差。由Model1、Model2、Model4 和Model5的对比可知，在2层卷积层之后，识别效果趋于稳定，但是模型的FLOPS 显著增加，综合以上分析，本文实验采用Model2的网络结构。

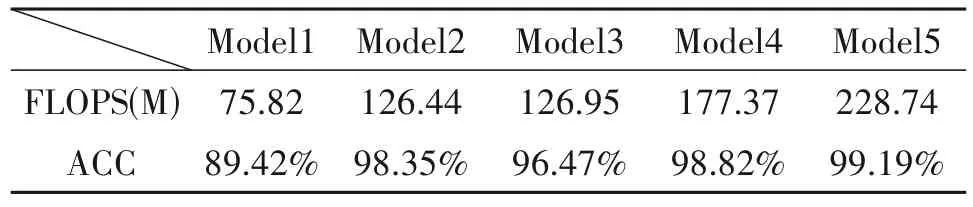
表2 各模型的参数量和准确率Tab.2 The number of parameters and accuracy of each model

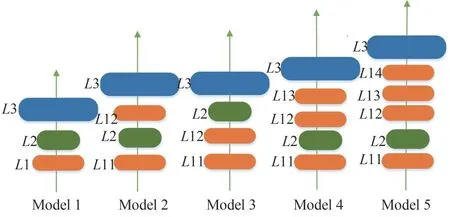
图6 网络模型结构的分析（L1代表卷积层，L2代表全局信息构建模块，L3代表全连接层）Fig.6 The analysis of the structure of the network model（L1 represents the convolutional layer，L2 represents the global context block，and L3 represents the fully connected layer）

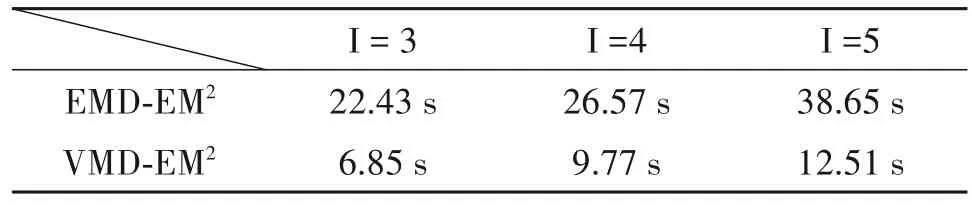
表1 数据预处理的计算时间Tab.1 The computation time for data pre-processing

在神经网络模型中，神经元的个数的选择是一个重要的问题。在CNN 中除了卷积层的个数外，卷积层的通道数以及卷积核的大小的选取对神经元的个数都有着重要的影响。由实验可知，本文网络选择2 层卷积层进行特征提取。由于1 × 1 的卷积核无法捕捉到数据的局部相关信息，本文对卷积核大小选取3 × 3 和5 × 5，两层卷积层通道数分别选取8、16、32、64 进行实验，分别考虑不同神经元个数所对应的网络的识别率和计算复杂度，其结果如表3～表4 所示。我们可知选择过多的神经元时，训练集中包含的有限的信息量不足以训练隐藏层中的所有神经元，因此产生过拟合的现象，并且随着通道数目的增多，网络中的FLOPS 和Params 都明显增加，其对应的计算复杂度明显增加。因此根据实验结果，本文网络采用卷积核大小为3 × 3，两层卷积层分别采用16和32通道的结构进行接下来的实验。

表3 卷积核大小为3 × 3时不同通道对应的网络性能Tab.3 The performance for different channels with convolutional kernel size of 3×3

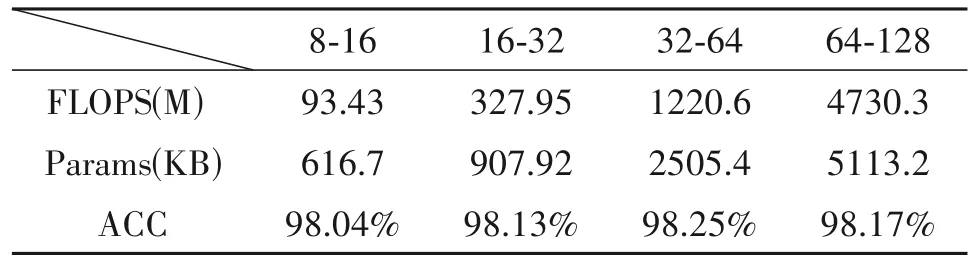
表4 卷积核大小为5 × 5时不同通道对应的网络性能Tab.4 The performance for different channels with convolutional kernel size of 5×5

为了分析模型的复杂度，本文使用所提模型与常用的网络模型CNN［10］以及Resnet［12］进行比较，使用模型的参数量（Params，parameters）以及FLOPS这两个指标来衡量模型的计算复杂程度，其结果如表5 所示。该模型与CNN 相比，准确度得到了明显的提升，并且在较低的复杂度的情况下，得到了比Resnet 模型更高的准确率，可见该模型在计算复杂度和准确率方面都有着较大的优势。

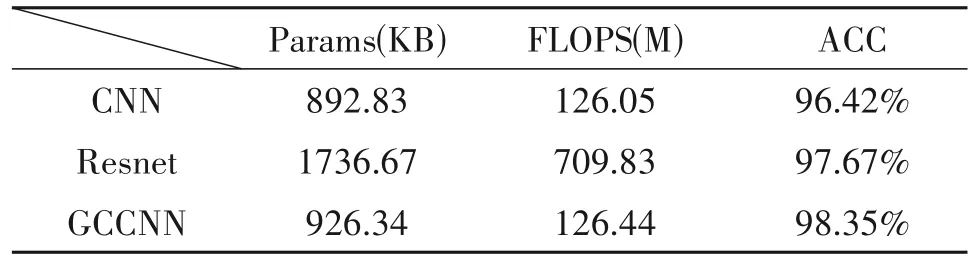
表5 常见网络模型的性能比较Tab.5 The performance comparison of other network models

由本节分析，本文对I/Q 差分信号进行VMDHilbert 谱的预处理操作，使用Model2 作为特征提取网络，这不仅使得本文算法拥有较低的计算复杂度，而且保证了良好的识别准确。

3.3 样本大小选取

通过数据预处理阶段，样本被转换成了希尔伯特谱，因此希尔伯特谱尺寸的选择成为了主要问题。从理论上讲，希尔伯特频谱的尺寸越大，它所包含的指纹特征就越全面，因此，在一定程度上增加希尔伯特频谱的大小是有益的。然而，网络模型对于输入为Nr·Nc的图片来说，其计算复杂度约为Ο(Nr·Nc)，随着输入图片尺寸的增加，网络模型训练的时间也会显著增加。另一方面，当希尔伯特谱的尺寸增大时，其包含的噪声等无用信息增多，它们会淹没信号的指纹特征，增大网络的识别难度。为了选择出合适的样本大小，本节选用ORACLE 中7 个同型号USRP 的IQ 信号，对其在不同信噪比下的识别性能进行研究。实验采取每个USRP 1000个样本，每个样本大小分别取200×200、300×300、400×400、500×500、600×600 和700×700，考虑到网络模型训练过程中存在着随机性，本文选用了10次实验的平均结果，其100个epoch的识别效果如图7。

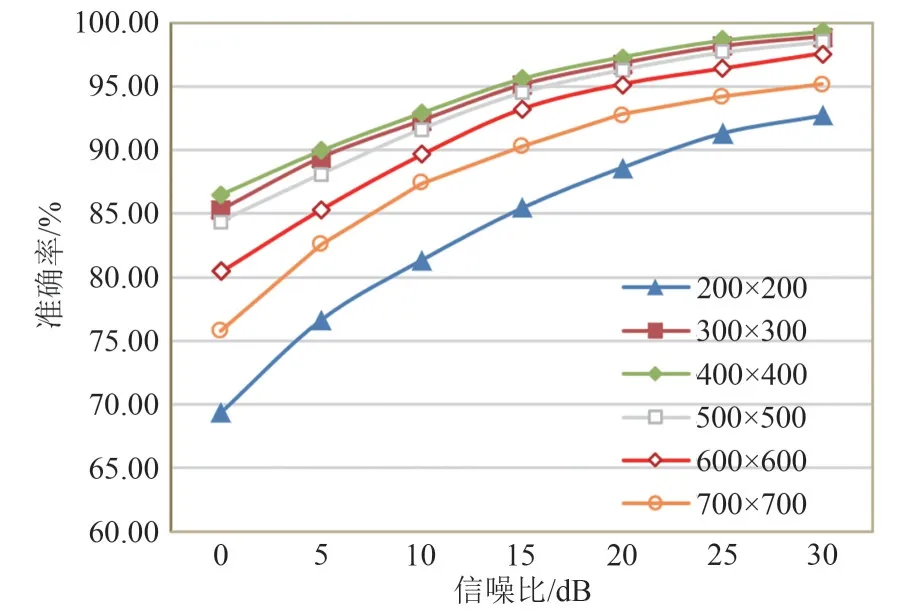
图7 不同尺寸希尔伯特谱的准确率Fig.7 The accuracy of different sizes of the Hilbert spectrum

从图中可知，当样本尺寸大于300×300时，其在不同信噪比下的准确率达到98.3%左右，已经能够满足识别任务的需要。但是，当样本尺寸大于600×600 后，其识别率明显下降，因为当样本尺寸过大时，其中包含大量的信号的数据信息和信道噪声，分布范围广、能量强，会改变希尔伯特谱的能量分布，淹没信号本身微弱的指纹特征。因此，考虑到识别率和计算复杂度，本文使用样本大小为300×300的希尔伯特谱进行实验。

3.4 算法性能分析

为了验证本文改进算法的有效性，本节进行两组消融实验。实验1：检验差分信号的有效性。该实验变量为原始信号Y(t)和差分信号D(t)，保持样本大小、超参数和模型结构不变。实验2：检验改善网络结构的有效性。该实验的变量为CNN 和所提网络模型（GCCNN，global context convolutional neural network），保持信号预处理阶段和样本大小不变。考虑到网络模型训练中的随机性，本文选择了10个实验的平均结果，消融实验的结果如表6所示。

表6 原信号与差分信号之间的消融实验Tab.6 The ablation experiments between Y(t)and D(t)

Y(t)-CNN和D(t)-CNN 的结果表明，后者的准确率有明显的提升，因此，由差分信号得到的希尔伯特谱能够有效地反映低频成分的特征随时间的变化，有利于模型进一步提取指纹特征。D(t)-CNN和D(t)-GCCNN 的结果表明，后者的准确率得到了一定程度的提高。因此，本文所提出的网络模型能够弥补希尔伯特谱的稀疏性带来的权限，有效地提取到数据中的全局相关特征，提高了网络的识别性能。综上所述，本文算法提升了原始基于希尔伯特谱的辐射源个体识别的性能。

3.5 噪声鲁棒性分析

为了探究本文算法的优越性，本节针对基于希尔伯特谱的辐射源个体识别现有算法进行一系列的比较实验：（1）EMD-EM2［8］，（2）VMD-EM2［9］，（3）EMD-Resnet［12］，（4）Bispectrum-CNN［10］。为了保证实验的公平性，所有的比较实验都使用相同的数据并在相同的条件下进行。实际情况下，在有线信道中，如光纤和同轴电缆，噪声类型主要是加性的高斯白噪声。在无线信道中，电磁波通过多径传播即多次反射和折射到达接收器，此时信号的强度服从瑞利分布。在本文中，原始信号是在一个简单的实验环境中获得原始信号。为了探索所提出的方法是否能适应复杂的电磁环境。本文对高斯信道和瑞利衰落信道进行建模，分析本文算法在不同信噪比下的识别性能，结果如图8～图9所示。

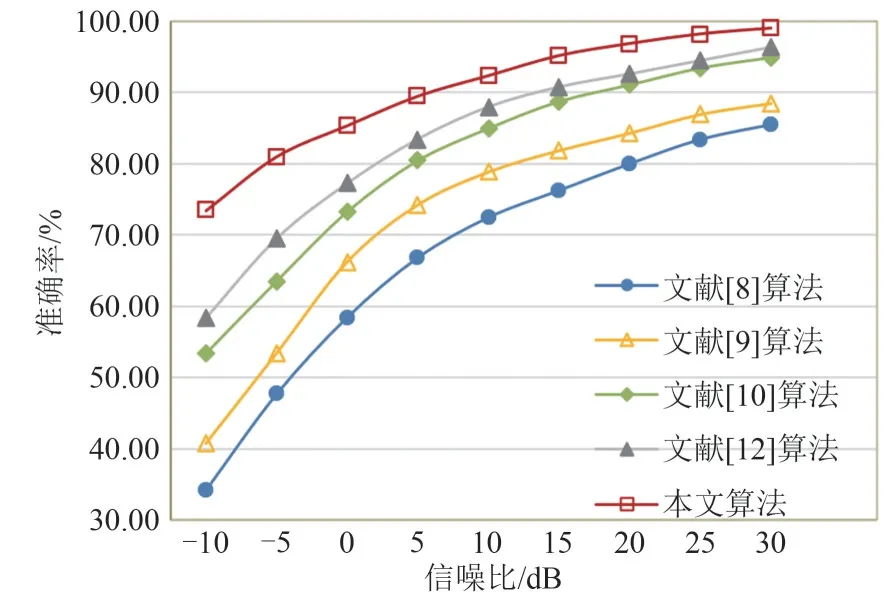
图8 各算法在高斯信道下的识别率Fig.8 Recognition rate of algorithms under Gaussian channel

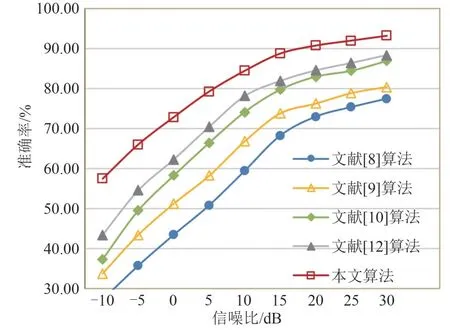
图9 各算法在瑞利衰落信道下的识别率Fig.9 Recognition rate of algorithms under Rayleigh channel

总的来说，基于深度学习的方法的准确率要高于传统方法的准确率，特别是在低信噪比情况下，基于深度学习的方法表现出良好的性能优势。在高斯信道中，本文算法和EMD-Resnet方法都比其他方法有更好的准确率，但是Resnet 模型使用多个卷积层和残差对数据进行特征分析，这增加了模型的复杂程度并且产生大量参数。在低信噪比情况下，EMD-Resnet 方法的性能下降明显，这是因为使用EMD 产生的希尔伯特谱存在模态混叠，不能很好地将信号不同频率成分分开，并且多层的特征提取使得网络过于关注数据局部的特征，破坏了数据本身全局信息的分布。而本文算法利用VMD 分解差分信号，更加有效地分解出信号低频的指纹特征，接着，根据数据的稀疏特点建立全局信息模块，使用简单的网络模型完成对数据细微特征的提取，这样不仅降低了模型的复杂度，而且保证了算法较高的准确率。在瑞利衰落信道中，识别率也会下降，因为衰落系数使信号的包络随机变化，从而淹没了信号指纹特征之间的差异。然而，VMD 不仅可以分离信号的低频和高频成分，而且其分解过程使用了嵌入式维纳滤波器，可以减少噪声对信号的影响［15］，提出的网络模型能够有效分析信号的全局信息，并且在空间和通道注意力的同时作用下，能够赋予那些无用的噪声较低的权重，使得模型更加关注于有用特征的提取，因此，本文算法在VMD 阶段和模型训练阶段都起到了良好的降噪作用。综上本文算法在低信噪比下有着良好的识别效果，特别是在5 dB时能达到90%的识别率。

4 结论

本文结合信号处理和深度学习提出一种新的辐射源个体识别方法。利用7分类ORACLE 数据集进行实验，确定了所提算法的网络结构和模型参数。通过对比实验可以发现：与现有的基于希尔伯特谱特征提取的辐射源识别方法相比，本文算法不仅有着较低的计算复杂度，而且在低信噪比和瑞利衰落信道的情况下有着良好的识别效果。本文算法首次使用差分信号进行VMD-Hilbert得到希尔伯特谱，并且根据输入数据的特点对网络模型进行改进，这为接下来的研究提供了一个可行思路。当然该算法可以进行进一步改进，我们可以根据模型的识别效果探究信号的指纹究竟分布在哪些频段，并通过给信号的不同频段赋予不同的权重来进一步提升算法的性能。