基于风车桥耦合的高速铁路独塔斜拉桥速度参数及基础刚度阈值管理

韦子娥,罗桂发,邓建新

(柳州铁道职业技术学院建筑技术学院,广西柳州 545616)

引言

我国幅员辽阔，地形及环境复杂多样，其中，西南地区由于地处青藏板块与扬子板块交界、地质灾害易发，造就了多高山深谷、大江急流的险峻地形。桥梁横跨山川河流时，桥墩基础受水流冲刷、盐碱腐蚀、地震破坏等影响，可能导致桥墩变位、基础约束能力下降等问题。同时，该地区桥隧相连地段存在横风区，而高速化导致列车在相同风速下受到更大风荷载，轻量化也进一步降低了列车抗风抗倾覆性能。因此，基础病害、横风激扰、甚至两者叠加出现对桥上行车的安全平稳问题影响甚大。

针对桥梁基础病害问题，陈兆玮等[1]基于Fortran语言的自编程序，并结合有限元软件进行数据交换建立了车-线-桥耦合动力分析模型，分析研究了桥墩不均匀沉降对行车安全性的影响；CHEN等[2]基于车桥耦合模型分析了徐变效应引起的附加不平顺对连续梁拱桥行车影响；闫宇智等[3]针对桥墩横向变位和基础刚度变化对高速铁路行车安全性的影响进行了分析，并得到了变形限值。而本文将考虑基础刚度与桥墩刚度下降两类情况。

针对横风下车辆过桥安全运行问题，PROPPE等[4]研究了非稳态横风下车辆稳定性，其基于欧洲标准中的中国帽标准阵风开发的风载激励是一大特点；ZHANG等[5-6]针对山区城市地铁列车行驶于高架线路跨越江河时遭遇横风情况进行了初步探究，山区高墩桥梁背景及风速的山地加速效应是其一大特点。而本文将针对风速与车速参数进行分析并给出相应安全阈值。

针对车桥耦合系统的模拟问题，翟婉明院士团队[7-8]考虑轨道结构参振并引入动态轮轨接触，利用自编程TTBSIM平台搭建了大系统耦合模型，很好解决了车-桥振动的基本问题并应用于实际工程案例中；夏禾团队[9-10]考虑基于土木工程有利条件，考虑蛇形运动及轮轨非线性接触，建立车桥系统空间耦合振动模型，并进行了后续研究；陈圣球等[11]采用SIMPACK搭建了多刚体CRH2车辆，在ANSYS中搭建桥梁模型，通过联合仿真对斜拉桥进行了车-桥振动分析。而本次采用了基于SIMPACK-ANSYS的刚柔耦合模型建模方法。

以上文献较少针对西南地区高铁建设中的横风激扰并伴随基础刚度下降对列车过桥影响分析，但该地区桥梁结构基础病害叠加列车过桥时横风激扰问题对列车安全运行极为重要。鉴于此，基于某西南地区新建高铁线路，利用SIMPACK及ANSYS联合仿真搭建高速列车-独塔斜拉桥耦合振动分析模型，研究列车过桥引起振动的问题，研究墩台基础刚度下降及桥墩横向刚度下降对车桥振动的影响；利用MATLAB生成脉动风场模型，研究脉动风加载对车桥振动的影响，以及不同列车车速、不同平均风速对车辆动力响应影响特性及其阈值。基于风车桥耦合振动计算独塔斜拉桥行安全行车的风速/车速及基础刚度/桥墩阈值，以此来探究基础病害与横风激扰对安全行车的影响问题。

1 工程背景

西南地区某新建高速铁路选线中段位于四川东北部，双线线路，期间线路跨越嘉陵江。桥址位于地势起伏的低山丘陵地区，河道蜿蜒曲折，结合线位顺直度、拆迁量情况及航道管理部门意见，独塔斜拉桥是较好的选型方案之一，纵向布置(42+104+180) m，桥面以上塔高93.91 m，桥面以下塔高21.50 m，桥面宽25.67 m，设置27对斜拉索、双索面平形布置，如图1所示，其中数字①～④代表对应的桥墩编号。

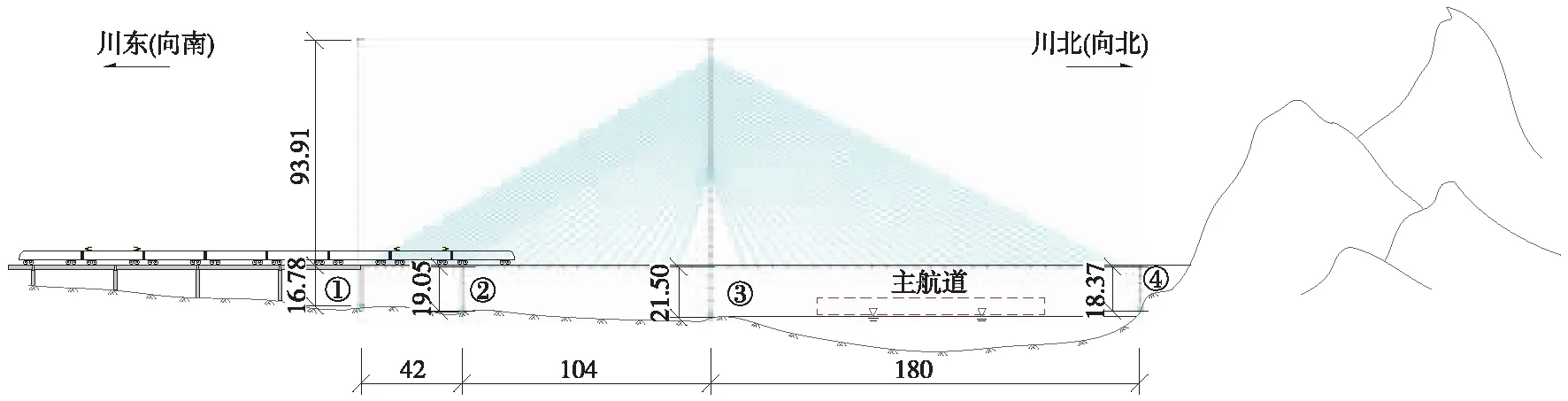
图1 独塔斜拉桥总体布置(单位：m)

2 风-车-桥分析模型

2.1 列车空间振动子模型

高速列车模型基于SIMPACK平台搭建，列车选用CRH3型四动四拖编组形式。每辆车之间横向、垂向为弱耦合，而横风作用主要为横向力作用，故列车模型中弱化了车钩。车辆简化为1个车身、2个转向架及4个轮对，每个刚性构件有2个平动以及3个转动，整车35个、整列280个自由度。车辆内部分层弹簧-阻尼系统中，垂向液压装置均考虑了非线性特性，弹簧考虑为线性模型，如图2所示。同时考虑了抗蛇行/垂向/横向减振非线性部件及止挡等，由Output Function描述在Force中引用。钢轨选择CN-60，车轮踏面类型为LMA，轮轨耦合模块选择基于FASTSIM蠕滑力计算方法。

根据D’Alembert原理建立车辆振动方程

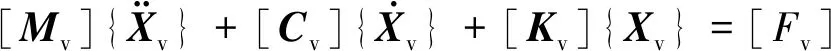
(1)

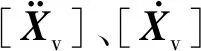
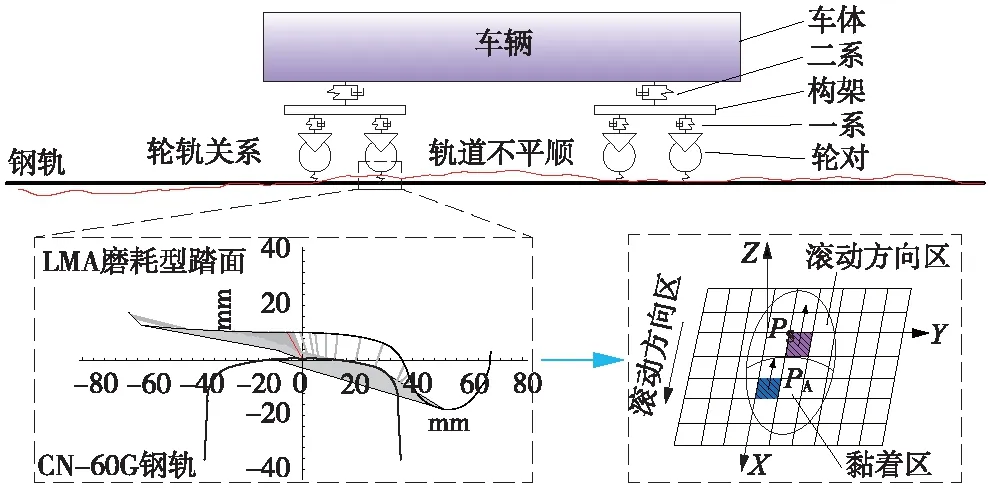
图2 车辆系统动力学模型

轨道几何不平顺谱采用德国低干扰谱，波长2～150 m，如图3所示。

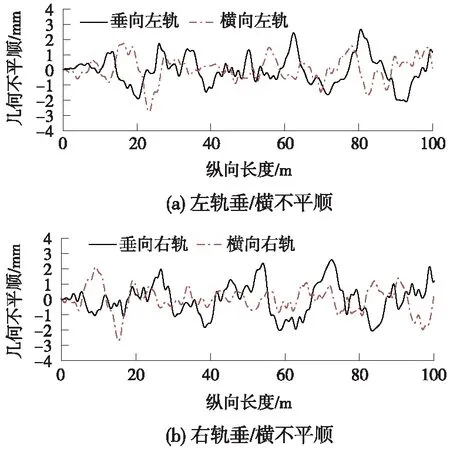
图3 线路几何不平顺样本

2.2 桥梁空间振动子模型

独塔斜拉桥子模型采用多自由度有限元模型，采用空间梁单元、杆单元、刚臂及等效基底弹簧等进行模拟。实际建模时，将斜拉桥考虑为多自由度柔性系统，在ANSYS中对桥梁进行子结构分析建模，生成所需*.cdb和*.sub文件，作为柔性体模型导入SIMPACK，各部件通过考虑非线性的相应力元连接。桥墩底部视为固定端，低阶模态信息如图4所示。建立桥梁振动方程

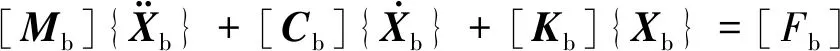
(2)

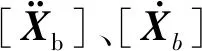
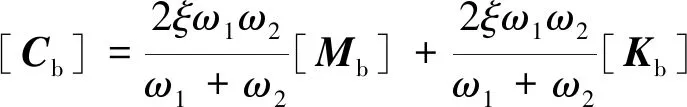
(3)

式中，ξ为阻尼比，考虑全桥和斜拉索单索结构阻尼(Rayleigh阻尼)，桥梁总体阻尼比为1.5%、单索0.15%；ω1及ω2为任两阶频率，参考频率考虑第1、第20阶。

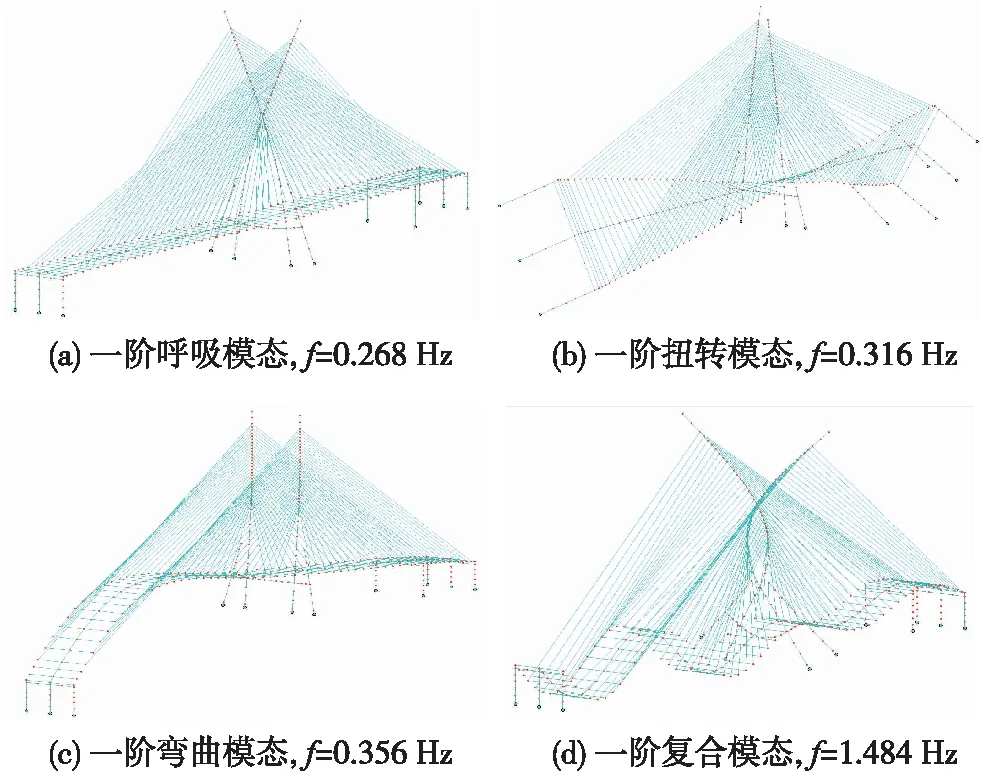
图4 桥梁低阶模态信息

2.3 车桥耦合振动模型

根据轮轨接触点力和位移与桁架桥节点力和节点位移的关系，得到车辆及桥梁受力表达式，实际计算中以轮轨接触面来进行车桥间数据交互的接口。构造车-桥动力学方程为

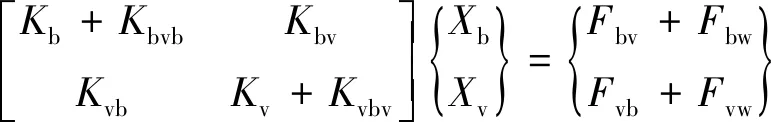
(4)

式中，Cbvb(Kbvb)和Cvb(Kvb)为由桥梁振动速度所引起的车桥附加阻尼及车辆附加阻尼；Cvbv(Kvbv)和Cbv(Kbv)为由车辆振动所引起阻尼；Fbv为车辆自重引起的移动载荷，Fvb为桥梁反馈给车辆载荷；Fvw及Fbw分别为车及桥所受到横风载荷。

对于独塔斜拉桥，可在有限元软件ANSYS平台建立，再通过确定界面模态综合法进行模态浓缩(剔除刚体模态)，以弹性子系统形式导入SIMPACK。最终搭建车桥模型如图5所示。

图5 车-桥耦合模型

进行动力学分析，模态计算采用子空间迭代法；而车辆多体动力学系统求解采用合适得数值积分方法，获得列车与轨道梁的动力学响应[9]。具体求解流程见图6。

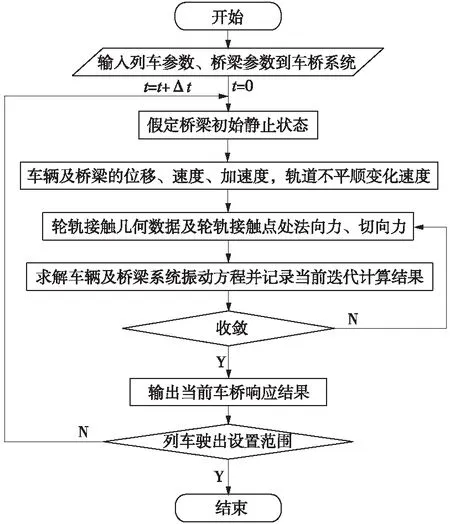
图6 车桥系统求解流程

2.4 空间脉动风加载方法

为更好表达空间脉动风场特性，每辆车质心所在位置脉动风并非完全同步，与风速及各点的相对位置有关，需考虑空间纵向及竖向的相干性(列车或桥梁长度方向及桥梁主塔高度方向)[12-13]。Kaimal谱是铁路领域常用谱密度函数

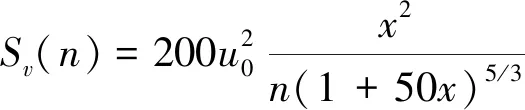
(5)

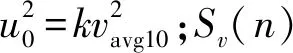
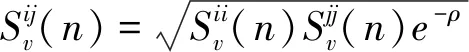
(6)

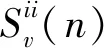
基于线性滤波法中自回归法(AR法)，采用MATLAB进行编程来实现空间脉动风场的模拟，所得脉动风场样本见图7(a)，加载位置见7(b)。

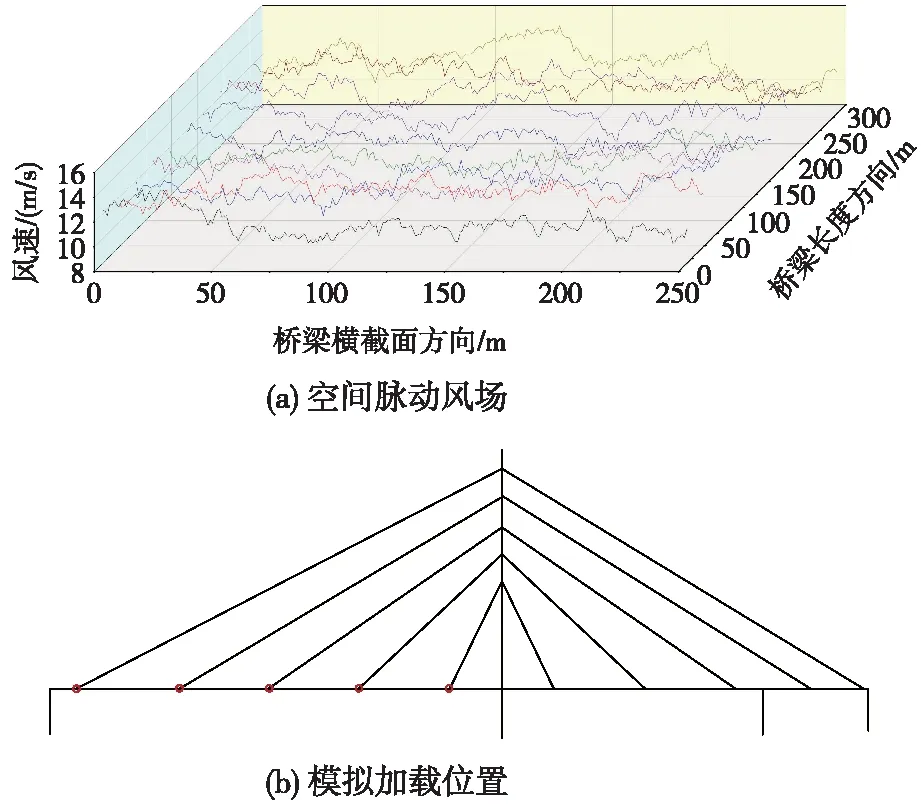
图7 空间脉动风场及模拟加载点

模拟风载最终加载到主塔、主桥墩、辅助墩各选定的分布节点上，并被简化为三分力，包括阻力FDb、升力FLb及力矩FMb，每种力还包含平均风力Favg及抖振力Fbf成分。将利用线性滤波法得到的脉动风速时程代入准确定常抖振力计算公式中，即可得到时域化的单位长度抖振力时程。具体公式为

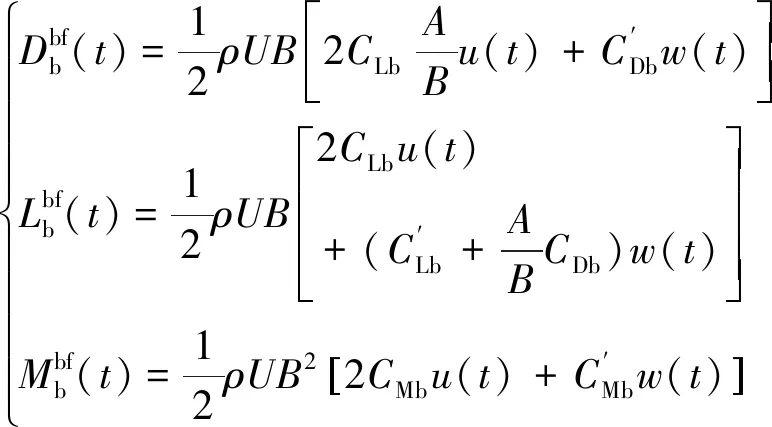
(7)

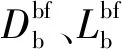
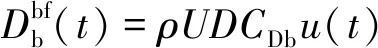
(8)

而车辆由于向前行驶而与横向风速相对运动形成的风速及偏航角，且风垂直垂向车体时定义为横风[14-15]。合成风速UR及偏航角β可表示为

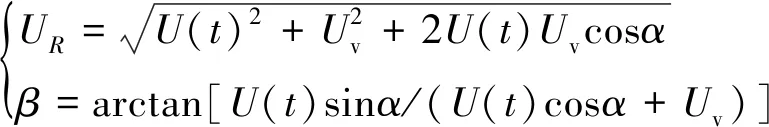
(9)

式中，Uv为车辆行驶速度；U(t)为横风风速；α为风向角，α=90°定义为横风。

车辆所受脉动风激励模拟为集中力和力矩(转化到各车质心)，各节车质心位置建立一个随质心运动的标记点，并建立一个力元，再将气动载荷添加到车体，这样即可使得脉动风激励作为外部时域载荷加载至车辆质心[16-17]。

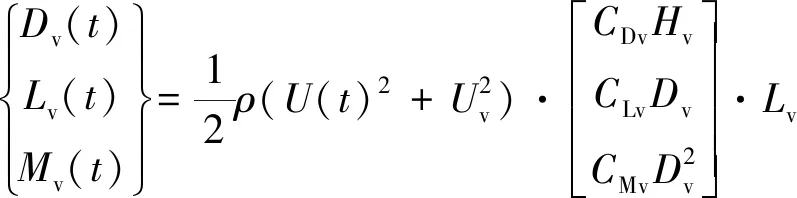
(10)

式中，Dv、Lv及Mv为车辆受到阻力、升力及力矩；CDv、CLv及CMv为对应风阻系数，具体如表1所示[18]；Lv、Dv及Hv分别为车长、宽、高。

表1 车桥组合的三分力系数

3 横风环境下独塔斜拉桥行车平稳性分析

3.1 无风时列车过桥振动动态分析

本节中选定工况为车辆以匀速v=200 km/h通过独塔斜拉桥，结果如图8所示。图8(a)～图8(c)为桥面(大小跨观测点)横向时频响应，图8(d)～图8(f)为桥面垂向时频响应，图8(g)～图8(i)为车辆时频响应。参考TB 10621—2014《高速铁路设计规范》[19]、GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》[20]等，轮轨采用脱轨系数(Q/P，阈值0.8)、轮重减载率(ΔP/P0，大于160 km/h时阈值0.8)来判断列车运行安全性，用车体加速度(竖向Acc_Z≤0.13g，横向Acc_Y≤0.10g)、平稳性指标来判断车体振动程度(竖向WZ≤3.0，横向WY≤3.0，否则指标不合格)。

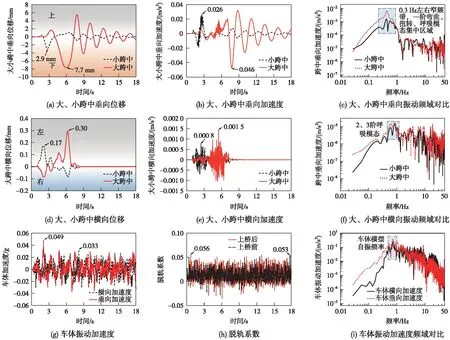
图8 车-桥系统动力学响应

由图8(a)可知，车辆驶过斜拉桥过程依次引起小跨中和大跨中位置点的垂向变形，两个峰值(分别为2.9 mm及7.7 mm)间距为74 m+92 m=166 m，数据与理论吻合。图8(d)可知，列车过桥先后引起了小跨中和大跨中的横向变形(横向峰值分别为0.017 mm及0.030 mm)，这是由于高铁车辆运行靠左行驶导致桥面整体向左微偏。图8(b)、8(e)可知，而车辆过桥引起的桥面垂向/横向加速度峰值分别可以达到：大跨中垂0.046 0/横0.001 5 m/s2，小跨中垂0.026 0/横0.000 8 m/s2。由图8(g)可知，对于车体可使得Acc_Z/Acc_Y达到0.049g及0.033g。图8(h)可知，上桥后轨下基础由刚性基础转为弹性基础，刚度不平顺与几何不平顺叠加作用使得脱轨系数略有增加。从频域角度分析可知，图8(c)、8(f)、8(i)可知，车辆过桥容易激起桥梁结构低频模态，尤其是前几阶中的弯曲、扭转及呼吸模态，而车辆横摆模态也容易被激起。

3.2 横风加载对车桥耦合振动影响

本节中选定工况为车辆以匀速v=200 km/h，风速10 m/s通过独塔斜拉桥，结果如图9所示。

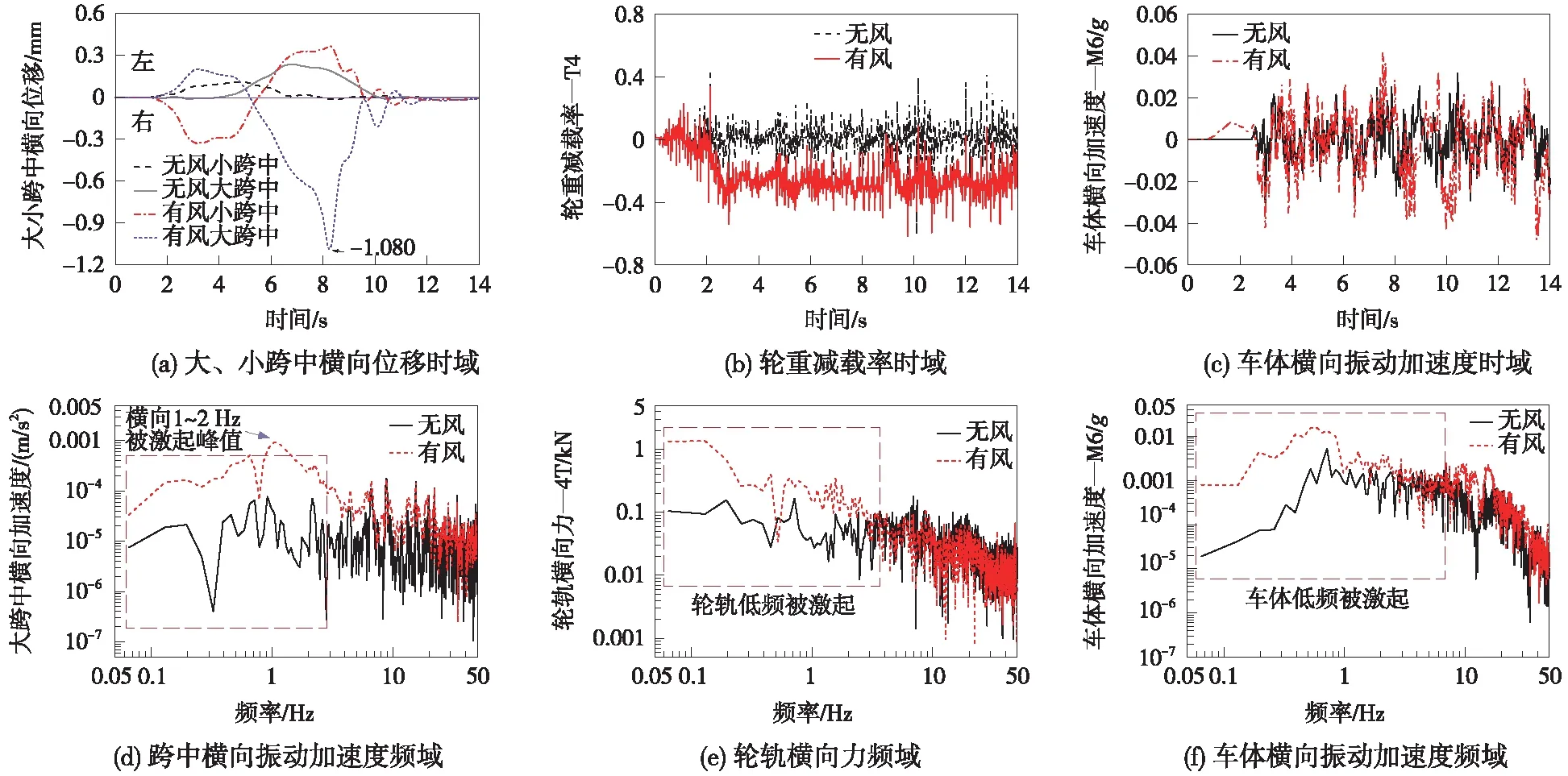
图9 横风加载对车-桥振动影响

由图9可知，无脉动风激扰时，列车过桥先后引起了小跨中和大跨中的横向变形且数量级很小，这是由于列车运行靠左行驶导致桥面整体向左微偏，而脉动风相对于车桥系统是从左向右吹会抵消列车偏载作用，故列车先经过小跨中时，桥面整体向右侧微偏。脉动风会使得桥面、轮轨、车体振动响应加剧，1～2 Hz低频振动被激起。

4 保证安全平稳行车速度及刚度参数阈值

4.1 风速及车速影响及其阈值

下面重点对不同横向风速下，非定常风荷载随车速变化对桥上列车走行安全及平稳性进行分析。计算车速为uv1=150，uv2=200，uv3=250 km/h，风速uw范围为5～35 m/s，结果如图10所示。

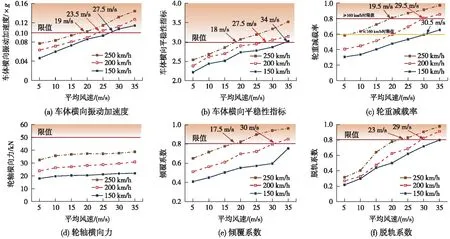
图10 桥上列车动力学指标随风速及车速变化情况

由图10可知，车辆动力学指标峰值均随平均风速及车速增大而增大，uw为5～35 m/s间阈值，得到桥上行车综合限速情况，见表2。

表2 桥上列车行车安全阈值

4.2 墩台基础刚度下降影响及阈值

在SIMPACK中利用弹簧阻尼(力元)模拟基底对桥墩底部进行约束。基于TB 10093—2017《铁路桥涵地基和基础设计规范》，按照“m”法计算基础各方向的约束刚度(其中，方向x，y，z分别为顺桥向、横桥向、垂向；rx，ry，rz分别为沿顺桥向、横桥向、垂向的转动方向)。采用4号桥墩基底刚度下降的方式模拟基础刚度变化，损伤程度代表基础刚度的降低量，刚度损伤范围为0%～95%(即刚度为原值的100%～5%)，车速为150～250 km/h，桥面风速10 m/s，结果如图11所示。

图11 车-桥振动随基础刚度变化规律

由图11可知，当列车过桥速度为150～250 km/h时，墩台基础横向刚度下降对列车走行性影响不明显，说明某一桥墩基础刚度下降对列车走行性影响较小，桥墩、桥塔、拉索、梁体、支座等构件会减小结构局部损伤对列车走行性的影响。墩台基础损伤程度发展至90%以上，跨中横向振幅和墩顶横向振幅才开始急剧增加，严重影响列车运行安全。

4.3 桥墩横向刚度下降影响及其阈值

桥墩横向刚度是直接影响列车走行性的关键参数之一。采用4号桥墩横向刚度下降的方式模拟损伤程度，刚度损伤范围为0～95%，车速为150～250 km/h，桥面风速10 m/s，结果如图12所示。

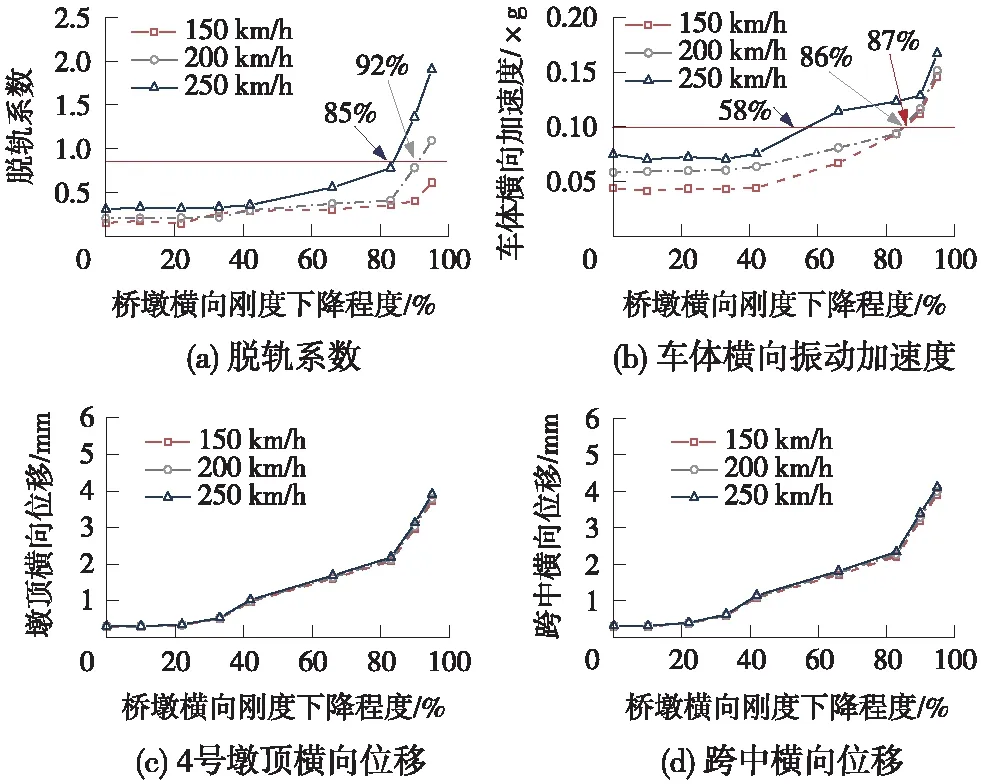
图12 车-桥振动随桥墩横向刚度变化规律

图12表明，轮轨、车体、大跨中及墩顶横向位移对桥墩横向刚度变化较为敏感，随着刚度下降迅速增加。另外，车速150 km/h时，脱轨系数未超限，车体指标超限值为损伤87%，则刚度损伤限值为87%；车速200 km/h时，两指标分别为92%、86%，则刚度损伤限值为86%；车速250 km/h时，两指标分别为85%、58%，则刚度损伤限值为58%。综合刚度限值见表3。

表3 综合刚度限值

5 结论

为探究横风下独塔斜拉桥行车安全的风速车速，基础刚度下降影响及相关阈值，利用SIMPACK-ANSYS联合仿真平台搭建了列车-轨道-桥梁耦合振动分析模型，研究列车过桥振动、脉动风加载、车速及风速、墩台基础刚度、桥墩横向刚度对列车走行安全平稳性的影响特性及其阈值，得出以下结论。

(1)车辆过桥容易激起斜拉桥结构低阶弯曲、扭转及呼吸模态及车辆横摆模态，车速增大导致车桥系统响应各频段能量密度变大(上移)，频域响应曲线逐渐向高频移动(右移)，桥面/车辆1 Hz以下低频振动易被激起，而脉动风在原条件基础上使得桥面、轮轨、车体振动响应进一步加剧，1～2 Hz低频振动被激起。

(2)车辆动力学指标峰值均随平均风速及车速增大而增大。车速为150 km/h时，平均风速综合限值为27.5 m/s(车体横向振动加速度首先超限)；车速为200 km/h时，平均风速综合限值为23.5 m/s(车体横向振动加速度首先超限)；而车速为250 km/h时，平均风速综合限值为17.5 m/s(倾覆系数首先超限)。

(3)墩台基础横向刚度下降对列车走行性影响不明显，桥梁其他构件会减小结构局部损伤对列车走行性的影响。当墩台基础损伤程度发展至90%以上，跨中横向振幅和墩顶横向振幅开始急剧增加，会严重影响列车运行安全。车、桥动力学响应随桥墩侧刚度减小而增大。另外，预设风速10 m/s，车速150 km/h时，桥墩刚度损伤限值为87%；车速200 km/h时，桥墩刚度损伤限值为86%；车速250 km/h时，桥墩刚度损伤限值为58%。