基于“自治自动”的数学教学实践与思考
——以“解三角形复习课”为例*
2022-11-15戚有建江苏省扬州中学225009
戚有建 (江苏省扬州中学 225009)
1 问题提出
上世纪二十年代,美国著名教育学家、心理学家杜威首先提出了“自治自动”教育思想,并于1919—1921年间来华访问和讲学.受杜威先生影响,陶行知、朱自清成为“自治自动”教育思想的积极传播者和实践者.陶行知先生撰文《学生自治问题之研究》对“自治自动”进行阐述:学生自己管理自己,自我评价,自己发挥主观能动,实现自我成长.朱自清先生的教育理念集中体现在他给母校扬州中学谱写的校歌中:“人格健全,学术健全,相期自治与自动,欲求身手试英豪,体育须兼重.”“人格健全,自治自动”也成了扬州中学沿承百年的教育主张.作为扬州中学的一名教师,笔者也在努力继承和发扬这一教育主张,并且将其与数学教学融合起来,充分发挥学生的主体作用,促进学生数学思维的提升,逐步实现用数学的眼光观察世界,用数学的方法研究世界,用数学的语言表达世界.
为了践行“自治自动”,笔者以“解三角形复习课”为题上了一节公开课,授课对象是扬州中学高一理科重点班的学生,他们基础扎实、思维敏捷、积极性高,有较强的合作精神和探究能力.本节课的设计定位是“问题由学生提、思路由学生想、方法由学生说、反思由学生悟”.新颖的教学设计、丰富的数学活动,催生了精彩的数学课堂,取得了良好的教学效果,受到听课教师们的一致好评.
2 教学案例
2.1 基本构想
解三角形是由已知的边角确定未知边角元素的过程.而正、余弦定理的作用就是将边角间的关系数量化,从而构建方程(或方程组),因此方程思想是解三角形的关键.如果已知的方程个数比未知的边角元素个数少,这样就变成不确定三角形,此时就可以研究三角形中的最值(范围)问题.
2.2 教学过程
(1)学生自治自动提出问题
情境三角形的6个元素(3条边和3个角)中知道几个就能解三角形?有哪些类型?
意图此情境帮助学生回忆正、余弦定理的内容,思考正、余弦定理的作用及解三角形的几种常见类型.
问题在△ABC中,已知b=7,B=60°,,求.(请填一个条件,然后解答问题)
意图以开放题的形式呈现,让学生自己填写条件解答问题,可以激发学生兴趣,启发学生思考,让学生学会自己提出问题,从而实现自治自动,提升数学思维.
教学中,学生首先想到的是下面两种方案:给角求边、给边求角.学生根据这两种方案很容易编题,例如下面的题目1、题目2.


(2)学生自治自动分析问题
追问比较题目1和题目2,哪个问题值得进一步研究(哪个问题复杂点)?为什么?
意图启发学生进一步深入思考,体会这两类问题的差异,虽然都是用正弦定理处理,但是题目2中三角形可能会有两解.此时学生很自然地会想到编写这方面的题目,例如下面的题目3、题目4.
题目3 (判断三角形有几个解)在△ABC中,已知b=7,B=60°,a=8,判断△ABC有几个解?(答案:2个解)
题目4 (判断三角形有几个解)在△ABC中,已知b=7,B=60°,a=5,判断△ABC有几个解?(答案:1个解)
教学中还有学生想到了给边求边,例如:
题目5 (给边求边)在△ABC中,已知b=7,B=60°,a=8,求c.(答案:3或5)
解析本题可以用正弦定理处理,也可以用余弦定理处理,可启发学生体会其中的差异.实际上用余弦定理简单,因为它将原问题转化为二次方程问题,如果用正弦定理,则转化为三角方程问题,而且解题步骤会多一些.
教学中,还有学生想到了给面积求周长,或者给周长求面积,例如下面的题目6、题目7.


解析题目6、题目7旨在帮助学生体会正余弦定理的作用是将边角间的关系数量化,从而构建方程(或方程组),而在具体处理方程时可以一解到底,也可整体处理、设而不求.
(3)学生自治自动解决问题
学生的主动性被激活了之后就愿意思考、乐于思考.以上面的题目3为例,在“有几个解”这个重难点上,学生经过思考想到了很多好的解法:
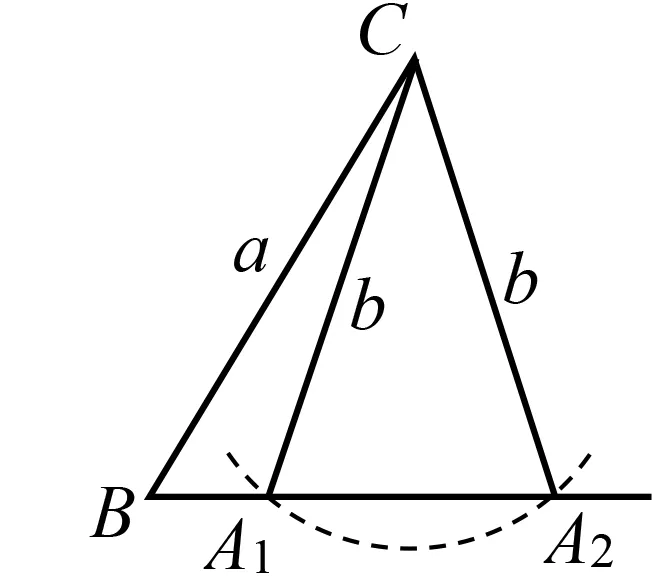
图1
解法1(交轨法)先作∠B=60°,然后在一条边上取BC=8,再以C为顶点、7为半径画圆(图1),因为圆与∠B的另一条边有两个交点,所以△ABC有2个解.

解法3(余弦定理法)在△ABC中,由余弦定理得c2-8c+15=0,解得c=3或c=5,所以△ABC有2个解.
(4)学生进一步提出问题
如果已知的方程个数比未知的边角元素个数少,则三角形不确定,此时就可以研究三角形中的最值(范围)问题.例如下面的题目8、题目9.

题目9 在△ABC中,已知b=7,B=60°,求△ABC周长的最大值.(答案:21)
题目9实际上可以归结为题目8,题目8的处理方法很多.
解法1构建基本不等式求最值

解法2构建目标函数(三角函数)求最值
解法3借助轨迹求最值
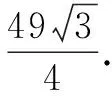
3 教学思考
3.1 “自治自动”是践行课标理念的有效途径
新课标强调,教师要更新教育观念,改变教学方式,让学生由被动学习转变为主动学习,由被动接受者转变为主动建构者.而自治自动的教育主张可以充分发挥学生的主体性,帮助学生自己主动发现问题、分析问题、解决问题,并且能及时地对自己的思维过程进行自我调控.自治自动可以促进高中数学教师教学方式和教学理念的转变,实现教学策略的改进,从而促进高中生数学学习方式的转变,实现数学思维能力的提升.
3.2 要努力培养学生发现问题和提出问题的能力
新课标中明确提出了“四基”和“四能”两大课程目标,“四能”具体是指提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力.爱因斯坦曾指出:“发现一个问题往往比解决一个问题更重要,因为提出新问题,需要创造性的想象力”.顾明远教授说:“新世纪的教育要求学生独立思考,敢想敢做,勇于创新,不能提出问题的学生不是一个好的学生”.可见,发现问题和提出问题是创新的开始.教学中,教师可以从问题的联想和类比、问题的延伸和推广等方面启发学生去发现问题和提出问题.
3.3 要让学生经历探究的过程,体验过程的艰辛
教学方式、学习方式的转变是新课标的本质要求,新课标倡导通过各种形式的数学活动,让学生亲身体验数学知识的发生、发展和形成过程.波利亚说过“学习任何知识的最佳途径都是由自己去发现,因为这种发现理解最深刻,也最容易掌握其内在规律”.现在的学生都是在“顺利”中长大的,生活中缺乏挫折和磨练,而通过一些“不顺利”的数学探究之路,可以让学生对探究历程的艰辛有深刻的认识,对科学道路的曲折有深刻的理解,同时也能培养学生坚强的毅力与不服输的精神.
