一道中考数学压轴题的解法探究及教学启示
2022-11-15刘艳萍江苏省苏州市工业园区景城学校215027
刘艳萍 (江苏省苏州市工业园区景城学校 215027)
通过 解题,学生可以加深概念的理解,深化认识概念的联系性,优化数学认知结构,训练数学思维,提高分析和解决问题的能力.笔者对2021年四川省自贡市中考数学试卷中的一道二次函数压轴题进行多角度的详细解析,并借此提出对教学的一点想法.
1 原题呈现
如图1,抛物线y=(x+1)(x-a)(其中a>1)与x轴交于A,B两点,交y轴于点C.
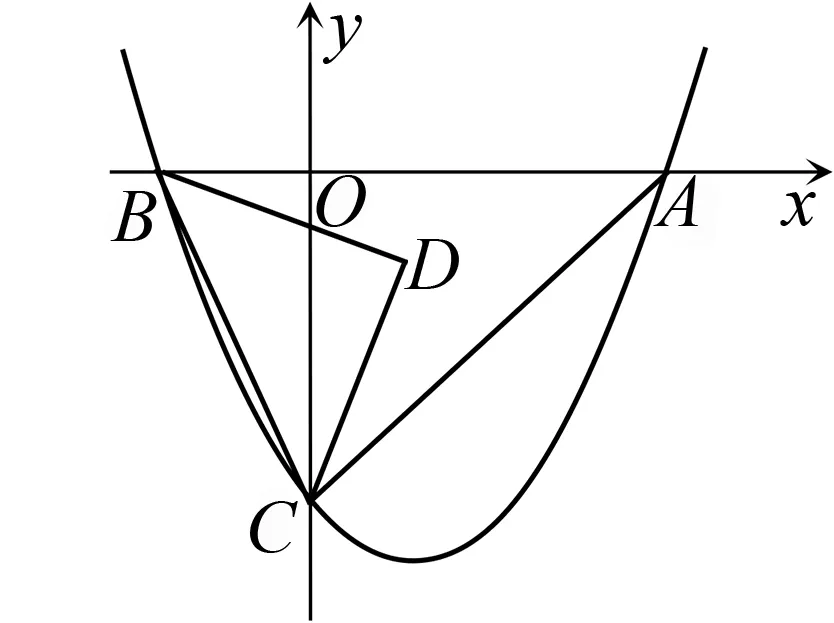
图1
(1)直接写出∠OCA的度数和线段AB的长(用a表示).
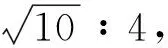
(3)在(2)的前提下,试探究抛物线y=(x+1)(x-a)上是否存在一点P,使得∠CAP=∠DBA?若存在,求出点P的坐标;若不存在,请说明理由.
2 试题解读
好题应具有以下“品质”:与重要的数学概念和性质相关,体现基础知识的联系性,解题方法自然、多样,具有自我生长的能力等.[1]本题是以二次函数为背景并嵌入三角形外心和等腰直角三角形等基本图形的压轴题.该题涉及的数学核心概念主要有:解方程、因式分解、二次函数、勾股定理、锐角三角函数、轴对称、全等三角形、相似三角形和圆等.本题涉及的数学思想方法主要有:化归思想、数形结合思想、方程思想和分类思想等.三小题难度由浅入深,第(1)小题考查解方程、坐标与图形的转换等;第(2)小题考查三角形外心的性质、处理相似三角形周长比的方法等;第(3)小题考查相等角问题的处理方法等,本小题的处理方法多样,可从构造相似三角形方向求解,也可从构造辅助圆方向求解,还可以从角的转换方向求解等.综上分析,该题在考试中具有很好的评价功能,同时也为后续教学提供了优良的素材.
3 解法探究
3.1 第(2)小题解法
由已知条件易得A(a,0),B(-1,0),C(0, -a),AB=a+1,OA=OC=a.△OAC是等腰直角三角形,其中∠OAC=∠OCA=45°.
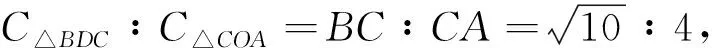
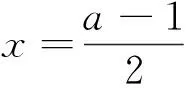
评析 解法1与解法2的相同之处都是从三角形外心的几何性质分析证明得到△BDC是等腰直角三角形,结合由第(1)小题得到的△OAC也是等腰三角形,可推得相似三角形△BDC和△AOC的周长比就是对应边的比,进而建立关于a的方程求解.两种解法的不同之处在于解法1直接利用边BC和CA的比,计算量相对少一些,而解法2先从“三角形外心是三角形三边垂直平分线的交点”的角度求出三角形外心点D的坐标,再用边BD和AO的比求解.
3.2 第(3)小题解法
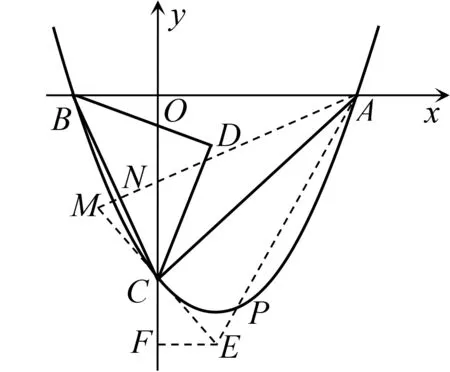
图2
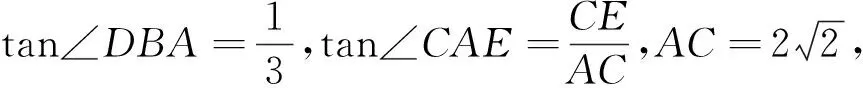


评析 从构造相似三角形和对称性两个方向思考问题.首先通过分析并构造出两个相似的等腰直角三角形,将三角函数值转化为相似比,求出点E的坐标,进而联立直线AE和抛物线解析式求得一解.再由点的对称得到角的对称,进而得到相等的角,利用对称性可求出直线AM的解析式,并联立抛物线解析式求得第二解.

图3



评析 从圆中角的转换和构造全等三角形方向思考问题.首先在由外心画出外接圆,将圆心角、圆周角等转换求得第一个点P的坐标.再利用对称性构造全等三角形求得直线AN的解析式,联立抛物线解析式求得第二个点P的坐标.

图4


图5

评析 从“角的转化”方向思考,体现了化归的数学思想.第①种情况利用“角的转化”证得直线AE⊥BC,进而求出直线AE的解析式,与抛物线解析式联立求出点P坐标.第②种情况利用“角的转化”证得∠CBO与∠PAE相等,根据其三角函数值也相等建立方程求出点P的坐标.
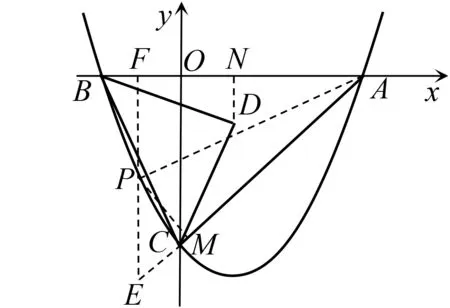
图6


图7
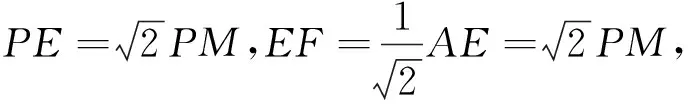
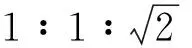
4 教学启示
4.1 教学中要重视数学概念的理解
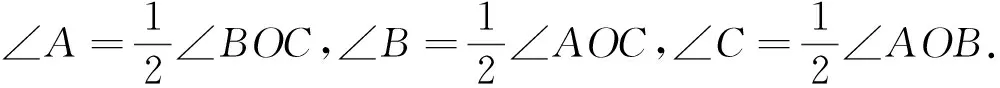
综上所述,教学中要让学生从多角度厘清数学概念的要素,明确数学概念的本质和概念之间的关系,以此强化对数学概念的深度理解.
4.2 教学中要重视主题教学
数学主题教学是在整体思维指导下,从提升学生数学学科核心素养的角度出发,以突出数学内容的主线以及知识间的关联性为方向对教材内容重组和优化而形成的一个相对独立的数学教学设计.数学主题根据具体的教学需求决定,可以分为以下三类:以重要的数学概念或核心数学知识为主题、以数学思想方法为主题和以数学学科核心素养为主题等.[2]例如根据第(3)小题可以设计以“相等角的处理策略”为主题的复习课.第一节课带学生梳理初中阶段不同章节中出现的相等角并完成基础练习.如在基本图形中有对顶角相等、角平分线分得的两个角相等;在两条平行线中同位角或内错角相等;在三角形中有等边对等角、等边三角形三个角都相等;在四边形中有平行四边形对角相等、菱形的对角线平分一组对角、矩形和正方形四个角都相等;在圆中有等弧或同弧所对的圆周角相等;在全等三角形或相似三角形中对应角相等;在锐角三角形函数中锐角三角函数值相同的两个角也相等;在一次函数中若直线的斜率k相同则直线与x轴的夹角相等……第二节课讲解相关的中考题目,在解题中加深巩固“相等的角”的处理方法.第三节课根据本主题内容安排相关测试并进行评价.通过主题教学与评价,学生对相等角的处理策略有了更深的理解,在解题中就能游刃有余,解题能力和思维能力都得到了发展.
数学主题教学正是从整体思维出发,在更高的观点下对数学教学中的各要素进行系统的综合考量,使其产生整体效益.教学中要重视主题教学,教师要把教学内容放到整体、主题中去全盘思考,才能有利于提升学生的数学核心素养.
