“三学”课堂的育人智慧解读
——以李庾南老师“三角形”新授课为例
2022-11-15江苏省南通市启秀中学226006
龚 震 (江苏省南通市启秀中学 226006)
著名特级教师李庾南老师及其团队近年来提炼出的“三学”(即学材再建构、学法三结合、学程重生成)作为一种操作范式,不仅能发挥数学知识、数学方法本身所具有的“知识”育人功能,更能在数学课堂教学中找到德育的切入点,潜移默化地渗透,在传授数学知识和培养相应能力的过程中育人,把传授数学知识和培养学生的观点、信念、情操等有机地结合,将“育人”根植于课堂的每一个角落.本文结合李老师“三角形(第一课时)”这堂课中的一些片断,谈谈对“三学”课堂育人实践智慧的几点感悟.
1 学程重生成,力探新知以求真
片断1生成三角形定义
师:先看几幅图片,组成这些图片的结构当中都有哪些我们学过的几何图形?
生:三角形,梯形,平行四边形……
师:其中最基本的图形是三角形,这些四边形中间有了一杠(对角线)以后就变成了三角形.为什么在生活中许多建筑要用三角形的结构呢?
生:稳定,三角形具有稳定性.
师:为什么三角形具有稳定性?那我们要看三角形的构造.三角形是如何形成的,怎样能够画出一个三角形?(请一位学生画,要求这位学生做慢动作一笔画,其他同学叙述他画的是什么、这个图形有什么特征.)
全班交流:这位同学第一个动作画的是一条线段,有两个端点.第二个动作又画了一条线段,这条线段与第一条线段共用一个端点.如果把一开始画的端点叫做首,另一个端点叫做尾,那么第一条线段的尾正是第二条线段的首,第一条线段的尾和第二条线段的首相连.再从第二条线段的尾开始画第三条线段,把“门”关起来了,形成了一个封闭的图形,此时三角形就画出来了.
师:这个三角形是如何形成的?组成三角形的基本图形是什么?这些图形有什么位置关系?
生:三角形是由三条线段首尾相连形成的.
师:首尾要顺次相连,任意三条线段能不能摆成首尾顺次相连呢?
生:要在同一平面内.

图1
(小组讨论什么样的图形是三角形,全班交流)
师:刚才多数同学很好,不翻书,在脑子里思考图形的特征.少数同学缺少自信心,翻书看书上怎么说的,自己研究归纳的知识才不会忘记(请学生回答问题,引导说出三角形的特征:不共线的三条线段首尾顺次相连所形成的图形叫做三角形).
师:这就是三角形这个图形的定义.一个图形的定义是对它的特征的抽象概括.因为三角形具有这样的特性,是不共线的三条线段首尾顺次相连的封闭图形,所以三角形具有稳定性.
教学赏析李老师的设计注重定义的生成过程,力探新知以求真,主要体现了四方面的育人智慧:(1)以大家熟悉的三角形性质——稳定性着手,抛出问题“三角形为什么具有稳定性”,体现了数学的求真精神、探索精神;接着用对图形特征的分析得到定义,由定义来解决问题,给了学生几何图形研究的套路,即图形的性质应回归定义研究,而图形的定义由组成图形元素的本质特征抽象概括而成,培养了学生回归本真的科学精神,提高了学生的抽象归纳能力.(2)从一步一步的画图,仔细寻找组成图形元素的关系、体会图形的本质特征,培养认真、严谨的习惯.在定义的生成过程中,李老师采取了多种教学形式结合,特意放“慢”节奏,有助于去浮躁、净化心灵,同时也使学生形成面对问题要有缜密、有条理地思考的习惯.(3)在定义的生成过程中,一步步让学生试错,一步步让学生自主优化结论,培养了学生严密的逻辑思维能力和不轻率盲从的科学态度.(4)在教学中对学生给予语言上的鼓励,给了学生自信、自强、独立的优秀品质.
2 学法三结合,人本融合引崇善
片断2三角形有关概念的辨析
在给出三角形的定义后,李老师给出三角形的要素(边、角)及表示方法,并补充了对边、对角、两角夹边、两边夹角的概念.
师:谁上黑板来指指哪个角是哪两边的夹角,哪条边是哪两角的夹边,哪个角是哪条边的对角,哪条边是哪个角的对边?(等待)大家有没有困难?自己在小组里先说说看.
(学生小组议论,全班交流)
师:如图(图略),边BA,BC的夹角是?
生:∠ABC.
师:你们发现了什么?边BA,BC的公共端点是B,而它俩的夹角的顶点也是B.那么∠C是哪两边的夹角?
生:AC和BC.
师:为什么?
生:边AC,BC的公共端点是∠C的顶点C.
师:∠A是哪条边的对角?
生:BC.
师:很好.三角形三个顶点,除去A还剩哪两个点?(B,C)由此可以找到它的对边是BC.AC的对角是哪个角?(∠B)为什么?
生:三角形三个顶点,除了A,C还剩B,所以AC的对角是∠B.
师:三角形的边除了用端点大写字母表示以外,还可以用一个小写字母来表示.自己总结一下,用小写字母表示对边的规律.
(学生自主探究后,完成寻找相应元素的练 习,略)
教学赏析(1)李老师提出问题后并没有急于探求答案,而是询问学生有没有困难,在小组里合作解决.合作学习是数学学习的重要方式之一.合作可以培养学生的整体观、团队意识,学会尊重他人,倾听他人.(2)教师引导学生不是一味地注重结果,更要注重过程以及思想方法的总结.李老师培养学生用数学思想方法解决问题的实践能力和创造能力,让学生学会独立思考,让数学知识转化为学生认识世界、发现规律乃至发明创造的智慧.
3 学材再建构,灵动自由指向美
片断3三角形的分类
师:请在纸上画一些不同特征的三角形.(请学生上黑板画)
师:以什么为特征画三角形,首先要有选择.听听这位同学介绍他画的三角形有什么特征.
生:第一个图是直角三角形,第二个图里有一个钝角,是钝角三角形,第三个图三个角都是锐角,是锐角三角形.
师:他画的这三个图形是按照什么特征来画的?
生:角的大小.
师:因此三角形按照角的大小分为三类:有一个角是直角的三角形叫做直角三角形,有一个角比直角大的三角形叫做钝角三角形,三个角都比直角小的三角形叫做锐角三角形.按照角的大小分类还有一类标准,以三角形有没有直角来分类,有直角的叫做直角三角形,没有直角的统称为斜三角形.所以斜三角形又可以分为两类:锐角三角形、钝角三角形.这是按角的大小来分的,还有其他的分类方法吗?
生:可以以边的大小来分.有两边相等的,有三边都相等的,还有没有两边是相等的.
师:这样分类正确吗?再听李老师说一遍,三角形可以分为有两边相等的,有三边都相等的,还有没有两边是相等的三角形.有没有重复的?
师生共同小结:有两边相等,有没有说第三边一定不等?(没有)因此第三边有可能相等,有可能不等.那么三边相等应该包含在两边相等的情形中,所以按边分先分为两类:一类有两边相等,这就是等腰三角形,还有一类没有两边是相等的三角形,叫做不等边三角形.两边相等不排除三边相等,因此等腰三角形又分为两类:一类底和腰不相等的等腰三角形,一类底和腰相等的等边三角形.
师:同学们谈到了腰、底就一定是什么三角形?
生:等腰三角形.
师:不知道是不是等腰三角形,三角形的这条边不能叫做腰.同样地,不是直角三角形,也不存在斜边、直角边这些概念.所以,三角形分类要有标准,我们可以按角的大小分、按边的大小分.(再次回顾刚刚分类的方法和结果,利用刚刚学习的知识练习并小结.)
教学赏析“三角形”这节内容比较简单,李老师在建构教材时并没有进行整章节设计,而是仅仅把定义——组成元素——分类这么一点点知识放在一起,看似起点很低,但是李老师这堂课的设计却有着“高观念”——即通过这节课去学习研究几何图形的方法.对于“三角形”这样一个简单的几何学习对象,研究什么,怎样研究?“片断1”中学生从图形的共性特征中总结生成定义;“片断2”中学生从图形的组成要素中明白了如何认识图形,“三角形”就是认识组成图形的要素——边、角中位置关系;“片断3”中学生从图形的个性特征中比较组成图形的元素边和角之间的特殊关系,“特殊情形”往往是重要的.相应的,“特殊化”也是发现和提出问题的重要方法.李老师通过以上的设计,为学生清晰地呈现了本节课的知识结构体系(板书设计如图2),让学生感受数学知识的“结构之美”.
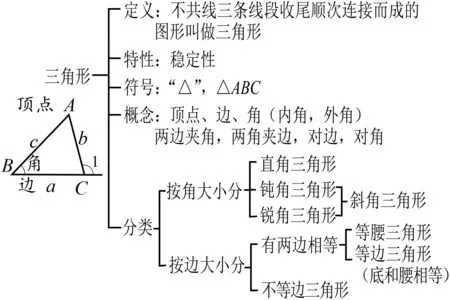
图2
4 课堂小结真正落实方法
片断4课堂小结
师:今天研究了三角形的概念,你们学会了哪些几何研究的方法?
①研究定义从哪里入手?(观察、概括图形特征.)
②研究几何图形从哪几个方面入手?(定义、符号表示、相关概念、分类等,接下来还会研究性质.)大家想想我们一定从三角形的哪些元素着手研究三角形的性质呢?(边、角.)
③我们不要限于已有知识,要有联想.例如三角形有内角,就要联想到有外角.研究问题要有序,分类要有标准.今天学习了数学中一个重要的数学思想——分类,分类要不重不漏.
④解决问题时,不是只关注结果,更要关注方法.
教学赏析从这节课可以看出李庾南老师都是以“何由以知其所以然”为教学追求,把数学的“思维之道”——数学地认识和表达事物的思想和方法阐释清楚,也就是要把内容所蕴含的数学思维方式解读出来,让我们能看清楚数学教学内容的育人价值,真正体现数学的价值即“思维之美”.
李老师以自己的亲身实践向学生诠释数学之美:让板书灵动呈现数学结构之美,用巧妙的问题链展现数学逻辑之美,创教室和谐氛围渗透数学育人之美.在潜移默化之中提升学生的审美素养,李老师的课堂处处闪烁“美”的智慧!
编者按:为密切编辑部与中学的联系,本刊编委第26次“走进课堂”,于2021年10月20日赴常州市第五中学听课交流.常州市第五中学创办于1906年,2000年通过国家级示范性普通高中省级验收,2008年被评为江苏省四星级高中.学校历百余年变迁,始终与时代共命运、与社会同呼吸,始终秉承“诚敬”校训,始终铭记“培植地方青年、养成有用人才,服务社会,担任复兴国家重任”的办学传统,积极践行“诚敬知行 悦美臻善”的办学理念和“综合发展、文理兼修、艺术见长”的发展策略,努力“为现在创造富有意义的校园生活,为未来创造丰富多元的美好可能”.
