多重短程有序准化学模型:有序原子对的对立与统一

王坤，邹星礼，曹战民，李重河，鲁雄刚

（1.上海大学材料科学与工程学院,上海 200444；2.北京科技大学冶金与生态工程学院,北京 100083）

基于经典准化学模型［1］，Pelton等［2～5］提出了改进的准化学模型，并将其成功应用于各类熔体热力学性质的描述，其是当前Factsage软件的主流热力学模型，取得了很大的成功.然而，与其它溶液模型一样，改进的准化学模型并不完美，仍有诸多不足需要改进.如，在处理互易熔体（如Na，Al//F，O体系）时，改进的准化学模型无法准确定义，在互易成分空间内随机位置处互易短程有序构型的能量.此外，当二元熔体中存在多重短程有序构型时，改进的准化学模型很难直接描述其热力学性质，通常需要耦合多态模型才能加以处理［6］.最近，Wang和Chartrand［7］在严格遵守质量守恒定律的基础上，规避了原始模型质量方程中的奇异矩阵问题，准确定义了互易短程有序构型的能量，据此给出了互易熔体能量的通用表达式，以实现对互易熔体在全成分空间内热力学性质的更准确预报.

在准化学模型框架下，有序原子对具有不可区分属性，导致其仅能直接处理含有单一短程有序构型时二元熔体的热力学行为.本文受量子力学中微观粒子具有波粒二象性启发，提出有序原子对同时具有可区分与不可区分两重属性的假设，在充分比对统计力学框架下原子和原子对属性的差异后，发现了有序原子对的对立统一规律，据此开发了多重短程有序准化学模型，该模型无需与多态模型耦合，可以直接处理含有多重短程有序构型时二元熔体的热力学性质，实现了复杂构型熔体热力学性质的准确预报.

1 理论与模型

1.1 准化学模型

准化学模型假定，在绝对零度时，二元A-B熔体的热力学性质近似于最近邻原子之间的键能总和.熔体中有3类键，分别来自（A-A），（B-B）和（A-B）/（B-A）原子对，其中（A-B）和（B-A）因完全等同而不可区分.据此，二元A-B熔体的吉布斯自由能可表示为

式中：nAA，nBB和nAB（mol）均为相应最近邻原子对在熔体中的含量；gAA，gBB和gAB（J/mol）为各原子对对应的键能.若A和B原子在熔体中的摩尔数分别为nA和nB，配位数为ZA和ZB，则熔体成分与各原子对数量之间的关系为

假设（A-A）键和（B-B）键的键能在A-B熔体中与其在各自纯组元熔体中一致，则gAA和gBB可表示为

纯组元A和B经混合形成A-B熔体，混合过程会有如下交换反应：

式中：ΔgAB为生成2 mol（A-B）键所需交换能.gAB由此可估算为

将式（2）～式（7）和式（9）带入式（1）可得：

在绝对零度以上，还需考虑构型熵对熔体吉布斯自由能的贡献.构型熵的获取需要计算（A-A），（B-B）和（A-B）对随机排布在三维点阵上的微观组态数，本质上是如何严格求解三维Ising模型.然而，三维Ising模型的严格解仍是目前物理学界的一大难题.在准化学模型框架下，二元熔体的构型熵是建立在一维Ising模型严格解基础上的近似表达式：

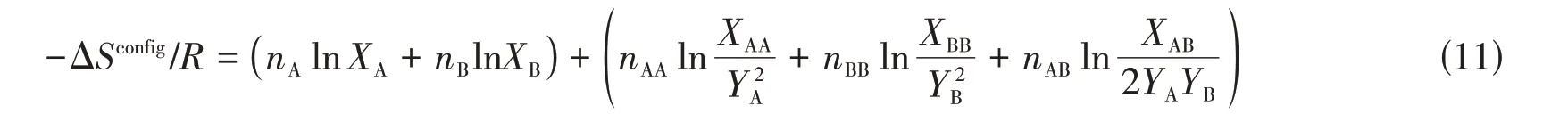
式中：R为气体常数；XA和YA分别为组元A的摩尔分数和配位等效分数；XAA为（A-A）对在熔体中的摩尔分数.物质的摩尔分数和摩尔数之间的定量关系表示如下：

式（11）中的第一项为基于Bragg-Williams点近似的理想混合熵；第二项则为来自原子对近似的构型熵.结合式（10）和式（11），准化学模型描述二元A-B熔体的吉布斯自由能可表示为

式中：T（K）为开氏温度；外变量T，nA和nB为计算时的设置条件；内变量nAA，nBB和nAB需要自由能最小化确定.各原子对在熔体中的平衡分布将使得熔体在特定成分和温度下的吉布斯自由能最低.因此，

当A和B原子的配位数均为2时，组元的配位等效分数与摩尔分数一致，式（15）将回归到经典准化学模型的表达式.此时，由式（16）可得到准化学反应（8）的平衡常数：

当ΔgAB=0时，原子A和B将在熔体中随机混合，和XAB=2XAXB成立，式（11）中第二项消失，熔体构型熵将回归理想混合熵，式（15）将变成理想熔体吉布斯自由能表达式.当ΔgAB值逐渐变得更负时，准化学反应（8）将持续向右进行，（A-B）对含量将逐渐在熔体中占据主导地位，熔体混合焓和混合熵将分别呈现字母“V”和“m”形状，表明熔体中A和B原子形成很强的短程有序构型.然而，经典准化学模型描述的短程有序位置始终在XA=XB=1/2处，限制了其实际应用于真实熔体热力学性质的描述.图1展示了由经典准化学模型表征的二元熔体的热力学性质.若熔体中短程有序出现在非中间位置处，运用式（15）描述其热力学性质需要为组元A和B赋予不同的配位数，模型所表征的短程有序位置由ZA/ZB控制.Pelton等［2］对准化学模型的这种改进，使其应用于真实熔体热力学性质的描述成为可能.图2展示了改进的准化学模型在ZA=2ZB=2.7548时所描述的二元熔体的热力学行为，此时短程有序位置可以出现在XB=2/3处.

准化学模型早期的改进版［8，9］定义A和B原子的配位数为不随成分变化的固定值.这种定义方式，在计算三元系时会出现问题.设想三元A-B-C熔体，其中A-B和B-C子二元熔体短程有序出现的位置分别由ZA/ZB和ZB/ZC确定.由于，

则A-C子二元熔体短程有序出现的位置已然固定而无法灵活选择.为此，Pelton等［2］引入配位数随成分的变化关系式：

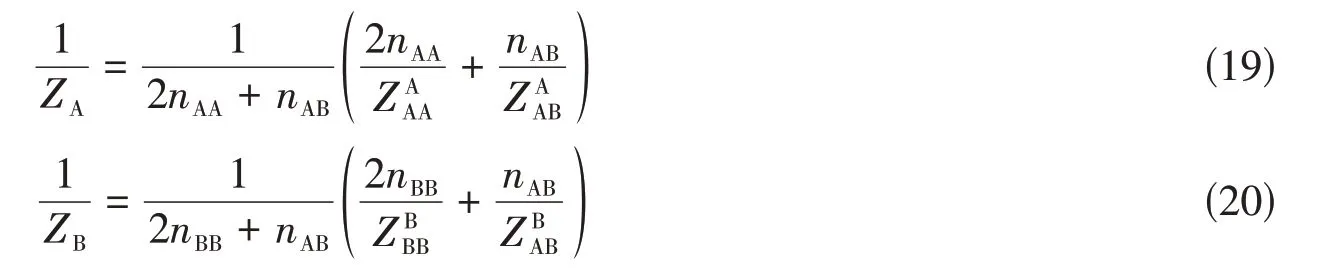
Fig.1 Enthalpy and entropy of mixing in the A-B solution calculated from the classic quasichemical model

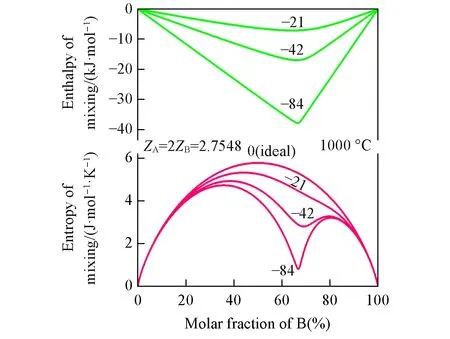
Fig.2 Enthalpy and entropy of mixing in the A-B solution calculated from the modified quasichemical model

设想将所有原子对分割成一个个原子团簇，则一个（A-A）原子对将包含个A原子，一个（B-B）原子对包含个B原子，一个（A-B）原子对则包含个A原子和个B原子.如此，式（21）和式（22）则代表真正的质量守恒关系.在实际模拟过程中，和代表纯组元A和B的配位数，在所有含A和B的体系中均一致，则只定义A-B二元熔体中短程有序出现的位置.

为了更好地拟合实验数据，Pelton等［2］先是将ΔgAB表示为成分的多项式函数：

后来根据Blander［10］的建议，又将ΔgAB表示为原子对分数的多项式函数：

式（24）可以理解为准化学反应的吉布斯自由能变化是构型依赖性函数.当熔体中存在很强的短程有序构型时，利用式（24）能够更方便地拟合实验数据.此时，短程有序位置会将实验数据分成两部分，靠近组元A区域数据可由系数拟合，组元B区域数据则由负责.因为，准化学模型的构型熵建立在一维Ising模型基础上，用其来处理三维真实体系时，若ΔgAB拟合为非常大的负值时，构型熵会出现不符合物理意义的负值.为了避免负构型熵的出现，Pelton等［11］将组元的配位数定义如下：

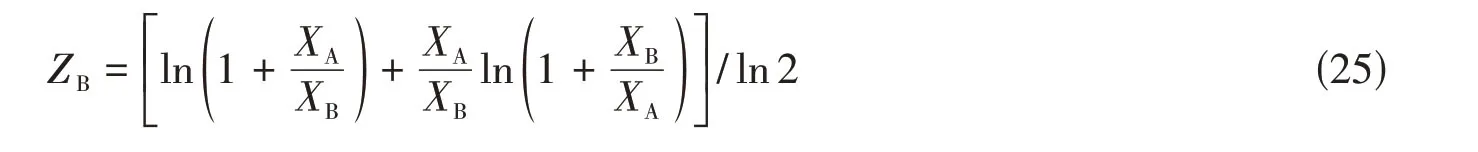
式中：XA和XB表示短程有序出现在熔体中的成分位置.在此位置，当ΔgAB为负无穷大时，熔体中有且仅有（A-B）对，且当配位数由式（25）定义时，体系的构型熵为零.

1.2 准化学模型的再发展

经典准化学模型及其改进版，只能处理单一短程有序构型熔体的热力学性质，根源在于模型中的短程有序原子对之间具有不可区分属性，固化了关于有序原子对统一性的认知.为了使准化学模型能够直接处理多重短程有序构型熔体的热力学性质，需要跳脱建立模型的原有概念和框架，提出新的假说和理论，在此基础上实现模型的再发展.

对立统一规律是物质的性质和核心，它揭示出自然界小到微观粒子和大到宇宙万物之间都具有对立和统一双重性，物质的对立和统一之间相互斗争和相互转化，推动着物质的运动、变化和发展.因此，本文提出假说，有序原子对之间也同时具有对立（可区分）和统一（不可区分）双重性.需要与统计力学中吉布斯基于微观粒子之间只具有对立性或统一性而提出的熵的悖论加以区别.Gibbs［12］认为，将两部分单原子理想气体进行混合，若所有原子都是全同粒子，混合时不产生额外混合熵，若是两类原子混合则会产生理想混合熵.这种额外熵的产生不具有连续性，它不随互混粒子之间的相似程度而连续变化.然而，有序原子对的对立与统一强调这两方面的转换具有连续性.熔体中的一个有序原子对是由两个不同类型原子组成的合作体，无论有序构型是否出现，有序原子对之间都会有很强的键能，同时有序原子对还受到周围原子对的影响，这与理想气体原子之间的情形完全不同.

有序原子对的对立面与统一面之间相互转化有两个内在因素：（1）原子对之间的键能；（2）原子对所处的配位环境.当全部有序原子对都具有相同的键能和配位环境时，有序原子对之间将具有不可区分的统一性，否则它们之间就呈现相互可区分的对立性.基于有序原子对的对立统一理论，本文首先将探讨双重短程有序准化学模型建立的基本情况，随后将模型框架进行一般化处理，最终建立多重短程有序准化学模型，以便能够处理具有复杂构型熔体的热力学性质.

1.2.1 双重短程有序设想二元A-B熔体具有双重短程有序构型，它们分别用（A-B）和（B-A）表征，在准化学模型框架下，熔体的吉布斯自由能可表示为

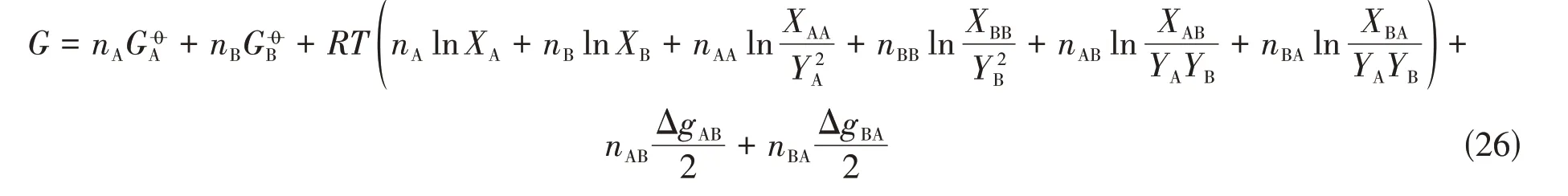
式中：组元的配位等效分数仍由式（13）定义.式（2）和式（3）将变化如下：

将式（27）和式（28）代入式（13），可得配位等效分数与原子对分数的关系式：

其中，对分数也需重新定义如下：

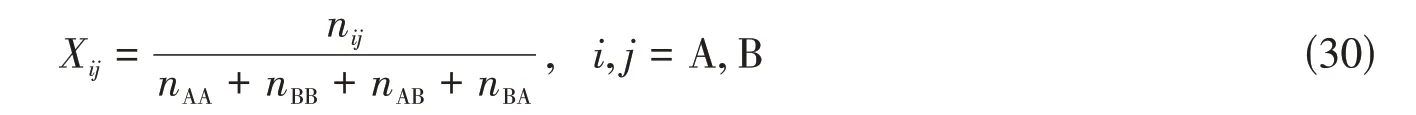
组元配位数随成分变化的关系式（19）和式（20）将变化为

将式（27）和式（28）分别代入式（31）和式（32），代表真实质量守恒关系的式（21）和式（22）将变为

应当指出，在经典准化学模型及其改进版中，nAB和nBA可以互换使用，都表示（A-B）原子对的摩尔数.同样适用于XAB和XBA，和和.然而，在双重短程有序准化学模型框架下，它们均各自表征不同的有序原子对.

特定温度和成分下熔体中的平衡对分数求解过程和准化学模型一致.吉布斯自由能最小化可设置：

式（35）和式（36）给出准化学平衡反应常数：

式中，指数求解如下：

式（37）和式（38）分别对应如下两个准化学反应：

将式（29）、式（33）和式（34）带入式（37）和式（38）即可求解各平衡对含量，各对含量再带入式（26）即可获得特定温度和成分下熔体的吉布斯自由能和其它热力学性质.图3为由双重短程有序准化学模型计算的摩尔混合焓和混合熵［13］，计算条件为1000℃，配位数为=1.3774，准化学反应能变为ΔgAB=ΔgBA=0，-21，-42，-84 kJ/mol.

观察图3发现，当ΔgAB=ΔgBA变得很负时，熔体在XB=1/3和2/3处会出现很强的短程有序构型，导致混合焓曲线在两短程有序位置之间会出现一个平台，而混合熵曲线则深度下凹.观察准化学反应（41）和（42）进行的方向不难理解，越负的交换反应能导致反应越发向后进行，这时在两短程有序成分之间，熔体中占主导地位的是有序原子对（A-B）和（B-A），致使两短程有序成分之间会逐渐出现溶解度中断区.

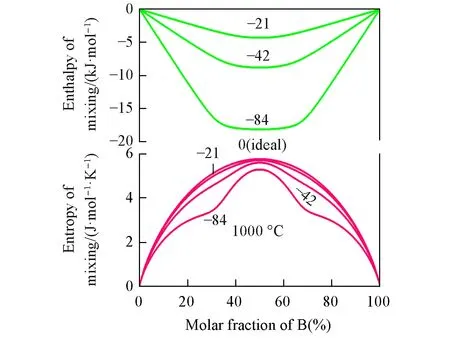
Fig.3 Enthalpy and entropy of mixing in the A-B solution calculated from the modified quasichemical model for twofold short-range orders

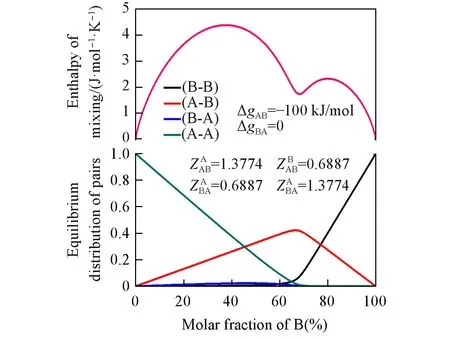
Fig.4 Entropy of mixing for the A-B solution calculated from the modified quasichemical model(MQMDPA)for twofold short-range orders

当ΔgAB=ΔgBA=0时，熔体中各原子随机混合，则有XAB=XBA=YAYB，XAA=和XBB=成立.这些关系式带入式（26）后，双重短程有序准化学模型将转变成理想熔体模型，构型熵将变成理想混合熵（图3）.这是双重短程有序准化学模型所能达到的第一种极限情况.当ΔgAB=ΔgBA，和成立，则nAB=nBA也成立，此时双重短程有序准化学模型已完全转变成Pelton等［2］提出的改进的准化学模型.若所有配位数设置成2，交换能与图3一致，则计算结果与图1完全一致.可见，当可区分有序原子对的键能和配位数完全一致时，全部有序原子对将变得不可区分.这是双重短程有序准化学模型所能达到的第二种也是最重要的极限情况.当ΔgAB→-∞和ΔgBA=0时，反应（41）将持续向右进行，不断消耗（A-A）和（B-B）对，从而驱使反应（42）不断向左进行.此时，与（B-A）对相对应的短程有序构型将消失，熔体中只存在与（A-B）对相对应的单一短程有序构型，如图4所示.这是双重短程有序准化学模型所能达到的第三种极限情况.

由于双重短程有序准化学模型的构型熵仍然是建立在一维Ising模型基础上，当交换反应能非常负时，仍然需要设置合理的配位数以规避负构型熵的出现.因熔体中现有双重短程有序构型，配位数计算式（25）将转变为

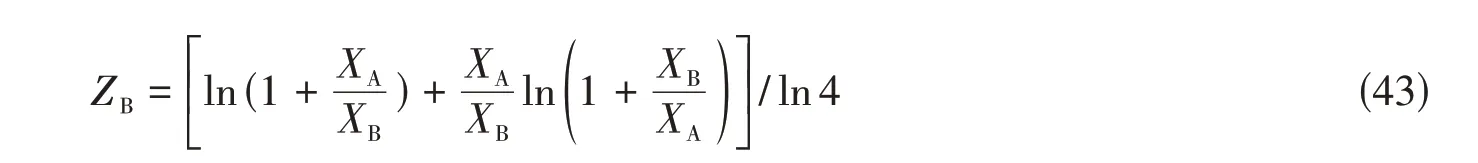
基于式（43）设置的配位数，当交换反应能趋于负无穷大时，熔体构型熵将趋近于零.此时，在某一短程有序位置上，熔体将只含有（A-B）对或（B-A）对，完全呈现短程有序构型.

1.2.2 多重短程有序为了满足更为复杂构型熔体的热力学处理需求，还对双重短程有序准化学模型进行了一般化推广，使其能够处理多重短程有序构型熔体的热力学性质.多重短程有序准化学模型可表示为

式中：Q表示熔体中短程有序构型出现的总数；k表示第k重短程有序构型；组元的配位等效分数仍由式（13）定义.式（27）和式（28）变为

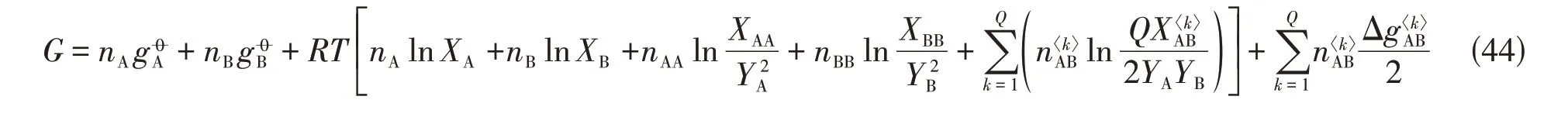
将式（45）和式（46）代入式（13）可得：

其中，对分数需重新定义为

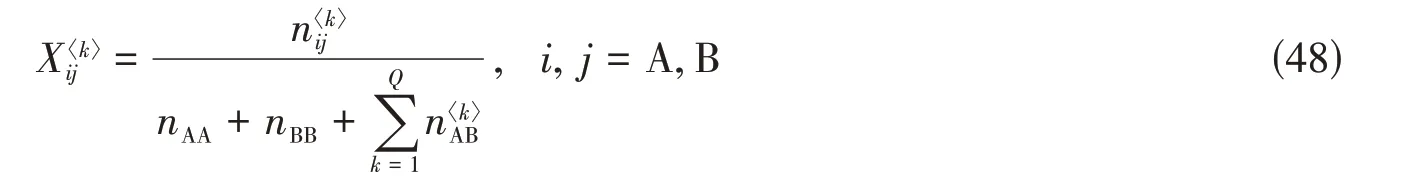
组元配位数随成分变化的关系式（31）和式（32）将转变为

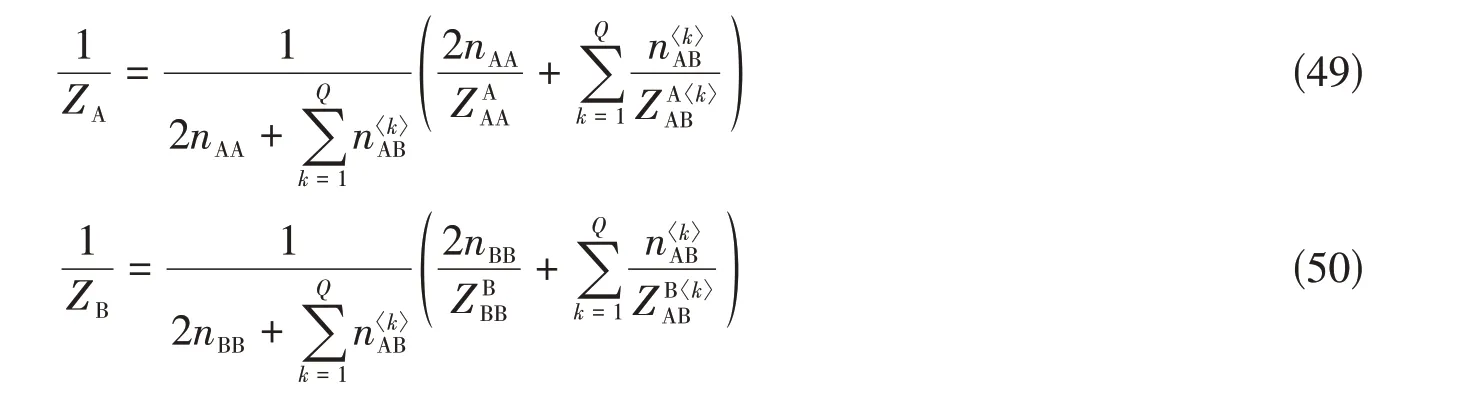
将式（45）和式（46）分别代入式（49）和式（50），代表真实质量守恒关系的式（33）和式（34）将变为

吉布斯自由能最小化可设置：

式（53）给出准化学反应平衡常数：

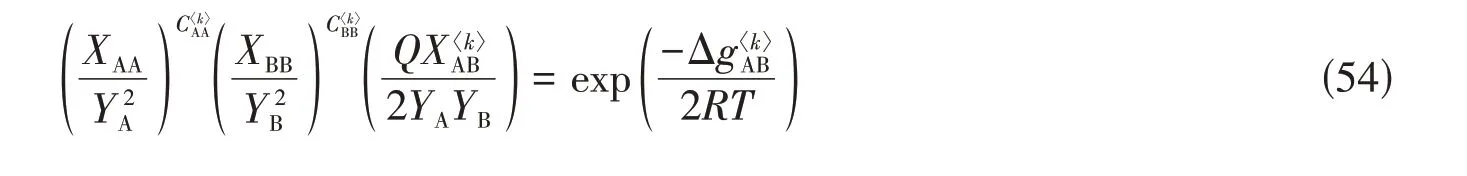
式中，指数求解如下：

式（54）对应如下准化学反应，

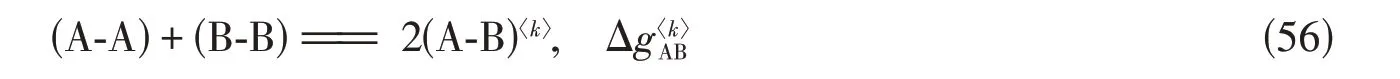
将式（47）、式（51）和式（52）带入式（54）即可求解各平衡对含量，带入式（44）即可获得给定温度和成分下熔体的吉布斯自由能和其它热力学性质.需要指出的是k将从1变化到Q，表明式（53）～式（56）的每个方程实际上代表k维方程组.

图5为由多重短程有序准化学模型计算的二元A-B熔体的混合焓和混合熵.计算条件仍然为1000℃，全部4个均赋值-100 kJ/mol.配位数根据下式计算：

式中：Q=4，因为本例处理的是四重短程有序构型熔体.由图5可见，4个短程有序位置处的构型熵均趋近于0，混合焓曲线则类似于二元系各稳定中间化合物的形成焓所围成的Convex-hull形状［14］，表明在给定的条件下，熔体在XB=0.2，0.4，0.6和0.8处呈现完全短程有序状态.在达到特定条件下，多重短程有序准化学模型将能分别回归到多种熔体模型.当所有趋近于0时，XAA=，XBB=和=2YAYB成立，式（44）回归到广泛使用的置换熔体模型；当所有相等且所有的有序原子对配位数一致时，式（44）回归到由Pelton等改进的准化学模型；当所有相等且所有配位数都为2时，式（44）回归到经典准化学模型；当Q=2时，式（44）回归到仍具有物理意义的双重短程有序准化学模型.因此，多重短程有序准化学模型适用于描述多种构型熔体的热力学性质，是一种通用的熔体热力学模型.

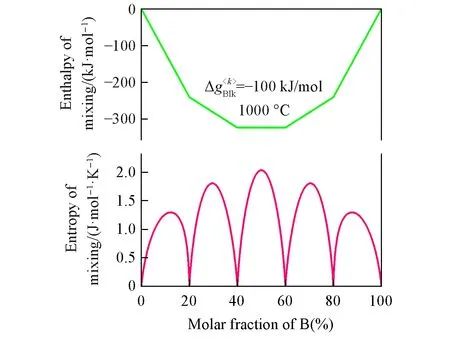
Fig.5 Enthalpy and entropy of mixing in the A-B solution calculated from the modified quasichemical model for manifold short-range orders(Q=4)

2 模型的实例验证

短程有序构型广泛存在于原子电负性差异较大的液态合金中，如碱金属与III，IV，V族金属的合金.前一种金属的电子可以转移到后一种金属上，形成非金属离子物质，从而产生短程有序化.统计力学表明，熔融合金的结构信息可以从热力学特性中提取［15，16］.Darken［17］定义的超额稳定性函数（Excess stability function，ES）可以很好地表征熔体中是否存在短程有序构型.超额稳定性函数定义如下：

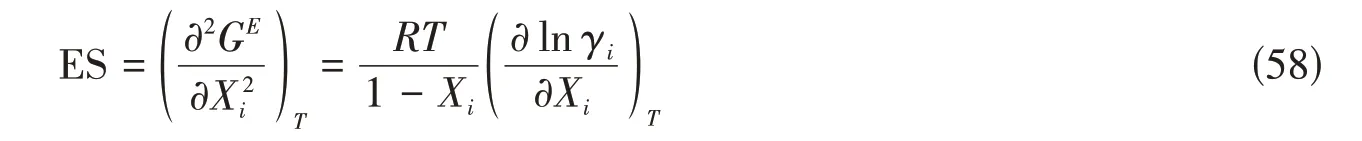
式中：GE为熔体的过剩自由能；γi为组元i的活度系数.使用Darken的超额稳定性函数对测量的热力学数据进行分析，结果表明，在Bi-K熔体中至少存在双重短程有序构型.为了简化起见，采用双重短程有序准化学模型来重现Bi-K熔体的各类实验热化学数据，以检验模型的合理性和可靠性.

Petric等［18］用电动势法在703～933 K范围内测量了K的原子百分数为0～80%Bi-K熔体的热力学性质.由测得的活度系数计算的过剩自由能、焓和熵均显示非常大的负值.由实测数据计算的超额稳定性函数，其曲线上有两个强峰，分别位于50%和75%K的附近，表明合金原子在此位置处存在较强的短程有序排列.据此，Niu等［19］采用含有BiK和BiK3两个物种的缔合物模型来描述Bi-K熔体的热力学性质，总共使用了22个模型参数.随后，Cao等［20］使用改进的准化学模型来描述液相的热力学性质，单一短程有序位置设置在BiK3附近，除配位数外共使用了12个模型参数.然而，较多模型参数的使用，在将其外推到多元熔体时，或许会导致一些预想不到的计算失真情况.本文采用双重短程有序准化学模型来处理Bi-K熔体，定义双重短程有序分别位于BiK和BiK3处，如表1所示，除配位数外，最终只需4个模型参数就能合理重现所有的实验数据.

Table 1 Coordination numbers and model parameters for the Bi-K liquid*

图6（A）～（C）分别给出了由双重短程有序准化学模型计算的温度为600°C时Bi-K熔体的过剩自由能、混合焓和混合熵.可见，计算结果很好地重现了实验数据.图7为600°C温度下活度系数（γK）的计算值与实验数据的比较，两者也能很好吻合.活度系数曲线在75%和50%K成分附近显现出异常的变化趋势，表明熔体中原子可能在此形成了短程有序排布.Bi-K熔体中出现的双重短程有序构型还可从超额稳定性函数曲线上更清晰地显示.如图8所示，模型计算和实验数据分析获得的超额稳定性函数曲线上均清晰地显示出两个峰，代表着双重短程有序构型可能出现在熔体中.计算结果与实验结果在峰的位置上存在一定的偏差，然而通过精调参数使得两者完全吻合是没有意义的，这是因为过剩自由能对成分的二次导数对自由能本身的数据精度非常敏感，而实验数据存在一定程度的测量误差.

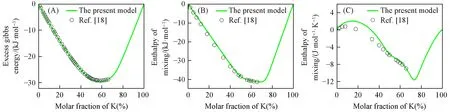
Fig.6 Calculated results for the Bi-K liquid using the modified quasichemical model for twofold short-range orders（A）Excess Gibbs energy；（B）enthalpy of mixing；（C）entropy of mixing.

应当指出，单从二元系的计算效果来说，缔合物模型和离子液体模型都能很好地处理两重以上短程有序构型熔体的热力学性质，其不足在于经常需要过多的模型参数来拟合实验数据，且将二元参数扩展至三元系时会出现难以预料的预测偏差，如无法预测三元熔体局部区域的液相分层现象［21］.与上述熔体模型的纯数学特性不同，双重短程有序准化学模型是建立在一定的理论基础上，是一种具有物理意义的溶液模型，因而能够有效克服其它溶液模型的不足.由表1和图6～图8可见，在使用较少的模型参数下，双重短程有序准化学模型仍能较好地重现实验数据，且较少的二元参数扩展到三元系乃至多元系也能确保获得相当可靠的预测精度.

Fig.7 Activity coefficient of K in the Bi-K liquid calculated from the modified quasichemical model for twofold short-range orders

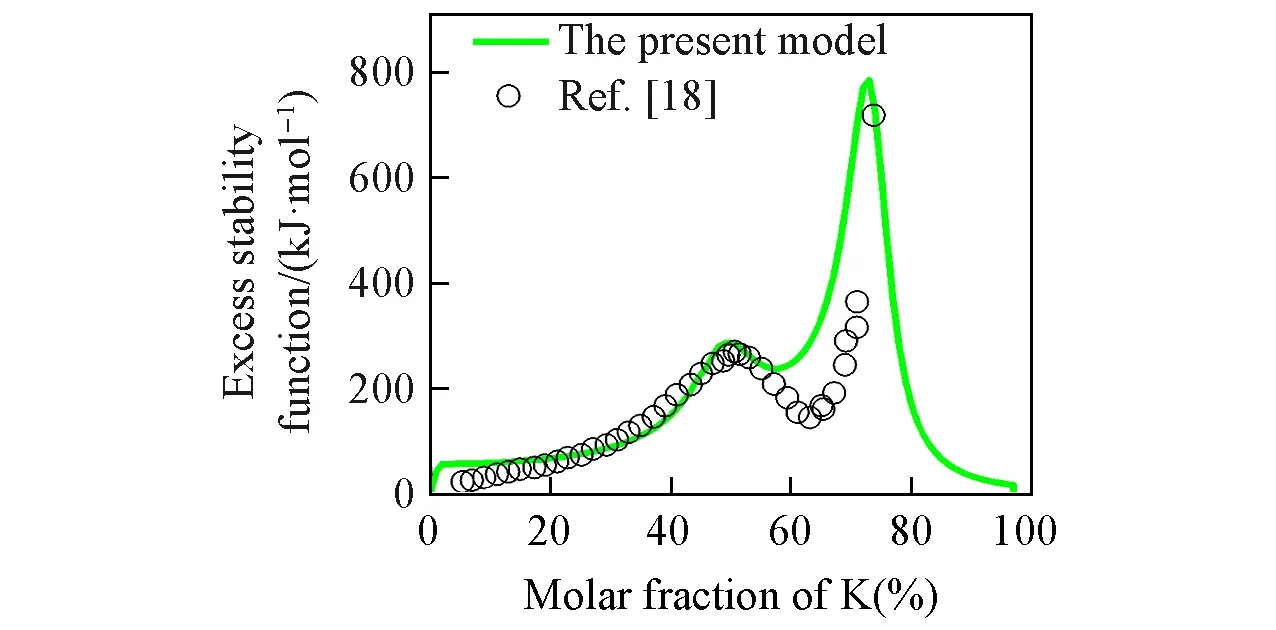
Fig.8 Excess stability function for the Bi-K liquid calculated from the modified quasichemical model for twofold short-range orders

3 结论

介绍了准化学模型及其改进版的开发过程以及模型的相关计算效果.针对准化学模型及其改进版无法直接处理多重短程有序构型熔体的热力学性质，提出了有序原子对的对立统一理论，据此开发了多重短程有序准化学模型，并展示了模型中各个公式的推导过程，讨论了在何种条件下能够转化为置换熔体模型、经典准化学模型、改进的准化学模型和双重短程有序准化学模型.最后，选取了至少具有双重短程有序构型的Bi-K熔体来验证多重短程有序准化学模型的可靠性.计算结果表明，除配位数外，只需要4个模型参数即可较好地重现所有实验数据.可以期待，相较于数值性的缔合物模型和离子液体模型，具有物理基础的多重短程有序准化学模型能够安全扩展到三元乃至多元熔体，实现多元系热力学性质的可靠预测.