定轴转动带电导体球全空间磁场分布求解及仿真模拟
2022-11-15黄霏月陈新光陈水源郭永健黄志高叶晴莹
黄霏月,陈新光,陈水源,郭永健,黄志高,叶晴莹
(1.福建师范大学物理与能源学院,福建 福州 350117;2.福建师范大学附属中学,福建 福州 350007)
导体球具有高度对称性,因此常常作为电磁学问题的研究对象.在达到静电平衡时,净电荷仅分布于导体外表面.若带电导体球绕定轴匀速旋转,其周围将形成一定的磁场,对此类磁场的求解是一种典型的静磁场边值问题,传统的解法利用磁矢势或磁标势结合边界条件解拉普拉斯方程或泊松方程,其计算过程相对繁琐[1-2];文献[3]在基于磁场叠加原理的基础上,巧妙地借助了磁矢势、电场强度和磁化强度之间的特殊关系,利用积分的方法求得带电球体的磁场全空间解析解,为此类问题的求解提供了新的方法.本文尝试分析导体球面的电荷在绕定轴转动的过程中其轨道运动的情况,由此出发,从而求出定轴转动带电导体球磁场的空间分布,为求解此类问题提供了一个新的方法.并利用Comsol有限元软件对该问题进行数值模拟,从仿真模拟的视角进行对比分析,以期达到验证理论分析结果准确性的目的.
1 方程及求解
1.1 电荷轨道运动的磁矩
为便于计算,假设半径为R的导体球面均匀分布着电荷,面电荷密度为σ,导体球以均匀角速度ω绕其直径旋转,讨论其全空间磁场分布.以球心为原点o,转轴为极轴,建立图1所示的球坐标系.当球体绕轴转动时,球面上的电荷以球面为运动轨道做定向运动,电荷运动的轨道角动量为

图1 定轴转动带电导体球示意图
(1)

原子中电子的轨道运动将产生磁矩,在玻尔氢原子模型中,电子在闭合的圆轨道上以角动量L绕原子核运动,闭合轨道上的电子运动形成一个小电流环,由经典电磁学知识可知,这样的一个小电流环可以看作一个磁偶极子,其磁偶极矩为
ul=ISn,
(2)
其中,I是电流环的电流,S是电流环所包围的面积,n是该电流环所包围面积的法向单位矢量.设电子轨道运动的半径为r,电子绕核运动的线速度为v,则有

(3)
式(3)即为电子轨道运动产生的磁矩[4].
类比电子轨道磁矩的推导过程可推得电荷轨道运动所产生的磁矩与轨道角动量的关系为
(4)
式中Q为轨道运动电荷的总电荷量,L为电荷运动的轨道角动量.
对上述所讨论的定轴转动带电导体球而言,其总电荷量为
Q=4πR2σ,
(5)
将式(1)、式(5)代入式(4)可得定轴转动球面电荷的轨道磁矩为
(6)
1.2 定轴转动带电导体球的磁感应强度
1.2.1 球面外部(r>R)的磁感应强度
带电导体球球面上的电荷绕轴做定向运动激发的磁场,等效于与圆心在同一直线上半径不同的一系列圆形电流所产生的磁场[5].磁偶极子在场点r处产生的磁矢势为
(7)
对于球坐标有

(8)
将式(7)代入式(8),对磁矢势求旋度可得r处的磁感应强度为

(9)
将式(6)代入式(9)整理后可得
(10)
式(10)即为以直径为转轴,定轴转动的带电导体球球面外部各点的磁感应强度.
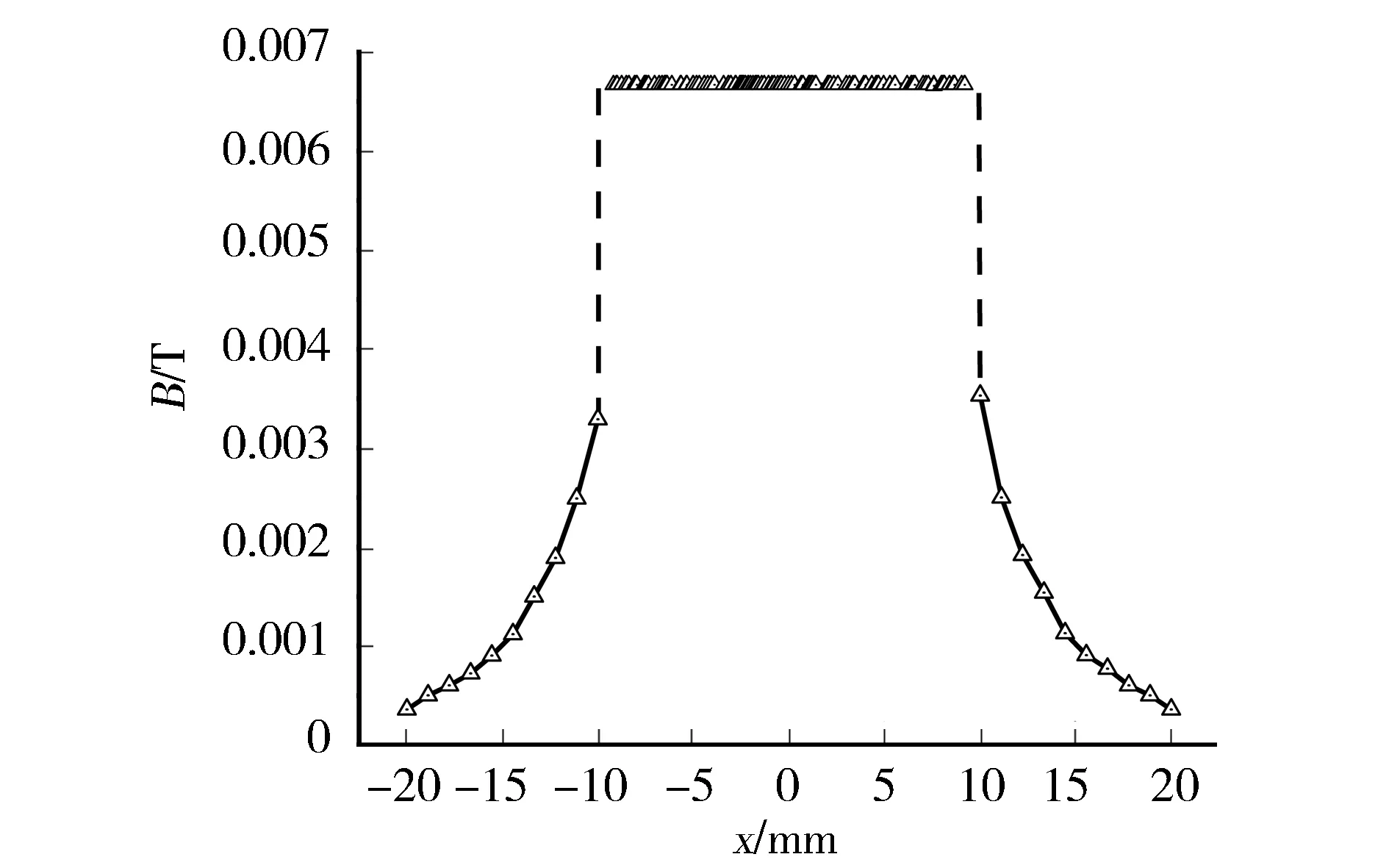
1.2.2 球面内部(r 对于R~R+dR的球壳,当其足够薄时,可近似看成一个球面,球面的面电荷密度σ=ρdr,其中ρ为球壳的体电荷密度. 球面电荷轨道运动产生的磁矩为 (11) (12) 比较式(11) 、 (12) 可得:均匀旋转带电导体球球面等效成均匀磁化介质球的等效磁化强度为 M=Rσωez. (13) (14) 式(14)即以直径为转轴定轴转动的带电导体球球面内部各点的磁感应强度. 综合式(10)、(14)可得 (15) 式(15)即定轴转动的带电导体球空间磁感应强度分布. Comsol是一款具有强大功能的多物理场仿真软件,软件自带多个求解模块使得模型建构更加便捷.利用软件中的AC/DC模块可对本文所讨论的定轴匀速转动带电导体球全空间的磁场分布进行仿真模拟. 本文在模型的建构上以转轴为极轴、球心为坐标原点建立球坐标系,选用良导体铜作为导体球的材料,旋转方向沿转轴的正方向,仿真过程所涉及的具体参数如表1所示. 表1 计算参数 2.2.1 全空间磁感线分布图 基于以上参数的设置,仿真得到的定轴匀速转动带电导体球全空间的磁感线分布如图2所示,图3为xz平面视图的结果. 图2 转动带电导体球全空间磁感线分布 图3 转动带电导体球全空间磁感线分布(xz平面视图) 2.2.2 轴线上磁场分布 为进一步分析其轴向磁场分布情况,提取模拟结果中z轴线上及x轴线上磁感应强度的数值,分别作与轴线上位置的关系图(见图4、图5). 图4 z轴线上磁感应强度变化情况图 图5 x轴线上磁感应强度变化情况图 利用Comsol有限元软件对定轴转动带电导体球空间磁场分布进行数值模拟,并对模拟结果进行分析,包括磁感应强度总体分布特征、仿真结果与理论结果对比、磁感应强度边界条件的一致性. 2.3.1 磁场总体分布特征 (1)由图2可以看出,定轴转动的带电导体球所产生的磁场在全空间的分布上具有较高的对称性,对称轴为转轴. (2)由图3可以看出,定轴转动带电导体球在球内部所产生的磁场与场点位置无关,是匀强磁场,方向沿转轴正方向. (3)由图2和图3可以看出,定轴转动带电导体球在球内部所产生的磁场是偶极型的,近似于把一个条形磁体放置在导体球的中心,导体球正上方与条形磁体的N极相对应.靠近转轴线上两极的磁感线分布最密集,远离导体球表面磁感线逐渐稀疏,磁场减弱. (4)对比图4和图5可知,在球外轴线上磁感应强度大小变化趋势相同,随着坐标位置的增大磁感应强度都呈现出减小的趋势,并且对比z轴与x轴两轴线上的磁感应强度大小的变化情况,可得z轴变化速度更快. 2.3.2 仿真结果与理论结果对比 根据仿真时所设置的各参数值,通过先前理论推导得到的定轴转动的带电导体球全空间磁感应强度的计算公式,即式(15),由MATLAB编程可以得到所建构模型的理论计算结果.并对两种结果得到的轴线上的磁感应强度随轴线上位置的变化情况展开对比分析.图6、图7分别为z轴、x轴线上磁感应强度大小仿真与理论的结果对比图. 图6 z轴线上磁感应强度大小仿真与理论结果对比图 图7 x轴线上磁感应强度大小仿真与理论结果对比图 由图6、图7可以看出,定轴转动的带电导体球全空间磁感应强度仿真计算值与理论值基本吻合,由此验证了前文方程及求解关于定轴转动带电导体球空间磁感应强度计算公式推导的准确性以及有限元仿真的可信性.在球内,即-10 mm 2.3.3 磁感应强度边界条件的一致性分析 (1)磁感应强度的边界条件要求当θ=0°或180°,r=R时,定轴匀速转动带电导体球所产生的磁场具有连续性,即B1n=B2n.理论推导的结果和仿真的结果表明在x轴线上球面处的磁感应强度大小不具有连续性,而z轴线上球面处的磁感应强度大小具有连续性,与磁感应强度的边界条件相一致. (2)磁感应强度的自然边界条件要求当r→∞时,B→0.由图6和图7可知在球外磁感应强度都呈现出随轴线上位置增大而减小的趋势,由此可以预见,随着轴线上位置的不断增大,在距离球面无限远处的磁感应强度将减小至0,与磁感应强度的自然边界条件相一致. 本文创新性地通过分析定轴转动带电导体球中的电荷在旋转过程中的轨道运动实现了对定轴转动带电导体球空间磁场的求解,该方法在计算上难度较小,且具有可推广性,可计算转动球体、柱体的全空间磁场分布.本文另一创新之处在于利用有限元仿真软件Comsol对定轴转动带电导体球在全空间形成的磁场进行仿真模拟,并将仿真结果与理论计算结果相对比,二者基本吻合,误差较小,由此不仅可以验证得出有限元法在模拟磁场分布上的可行性,而且使得磁场可视化,同时间接说明了理论推导结果的准确性.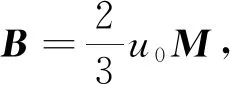
2 基于Comsol的模型建构
2.1 模拟参数的设定

2.2 数值模拟的结果



2.3 仿真结果分析


3 总结
