激光3D投影系统精度标定与补偿技术研究

刘馥宁，李丽娟，林雪竹，郭丽丽，程晓波

（长春理工大学 光电工程学院，长春 130022）

激光3D投影技术是工业制造技术中最先进的技术之一，已广泛运用在复合材料铺贴、零部件辅助装配等领域，其核心功能为双轴扫描振镜系统［1-2］。激光3D投影系统的标定精度直接影响后续投影工作的可靠性，即直接影响投影精度。因此，对于激光3D投影系统的精度标定有更高精度要求。为了提高激光3D投影系统的精度，需要对激光3D投影系统外部参数R、T以及振镜系统内部参数进行高精度标定，从而使得激光线能够准确地到达扫描范围内任意点。

早期的振镜标定技术主要是针对于振镜系统的“枕形畸变”这一原理性误差进行校正，常采用透镜或动态聚焦装置来进行校正，进而产生桶形失真或离焦误差等畸变。前者常采用理论推导相应公式或采用对实验得到的实际数据与理论数据对比进行补偿或校正。后者通常采用校正表法、最小二乘法、神经网络等方法进行补偿。韩万鹏等人［3］根据点坐标与振镜偏转角度间的函数关系建立校正模型，采用最小二乘法与分段线性插值相结合的方法进行校正。采用曲面最小二乘拟合的方法来建立坐标点的误差补偿曲面来提高校正精度，分段线性插值校正表的方法提高扫描速率。而对于系统外部参数的标定，郭丽丽等人［4］采用将投影观测值求解模型与外部参数校准模型相结合来完成激光投影系统的校准，利用Newton与四元数法来求解投影系统的外部参数R、T，完成激光投影系统的外参标定。

近些年来，对于激光振镜投影系统的精度标定不仅仅局限于原理性误差和外部参数。李旭东等人［5］提出基于单目视觉辅助标定二维振镜的方法，利用相机获得投影系统在标定板上的光斑的位置信息，通过建立振镜偏转角度与相机坐标系下光斑位置信息的转换关系，从而完成振镜系统参数标定，但其投影系统内部参数只考虑振镜间轴线间距的影响，因此使得系统标定精度不高。MANAKOV等人［6］在理想模型的基础上考虑入射光方向以及激光器位置两个因素，建立了一个更符合实际情况的复杂模型，引入更多振镜系统内部参数，采用全局优化的方法求解内外共12个参数，大大提高了标定精度。但该方法求解时间长且优化结果容易陷入局部最优解。涂俊超等人［7］建立振镜偏转角估计模型，并提出了一种分步标定激光振镜扫描系统的方法，将振镜扫描系统的校准参数分为方向参数与位置参数两部分，有效地解决了求解参数多、耗时长、容易陷入局部最优的情况。

本论文采用Newton迭代算法与PSO算法相结合的优化方法来进行优化求解。利用Newton迭代算法解算振镜偏转角、旋转矩阵R以及入射光方向矢量。在此基础上，利用PSO算法解算平移矩阵T以及激光器位置参数，该方法有效地解决了位置参数初值无法估计的问题。最后采用神经网络算法作为相应的补偿算法，对振镜转动角度偏差进行补偿。有效地提高激光3D投影系统标定精度。

1 原理

1.1 基本原理

激光3D投影系统主要是由激光光源、准直扩束装置、自动聚焦装置、双轴扫描振镜、光学反馈装置、合作目标、控制处理系统［8］等组成。如图1所示。

图1 激光3D投影系统组成

激光3D投影系统的工作原理：激光器发出的激光束经过扩束及动态聚焦镜组后，进入双轴扫描振镜模块，经过Y轴振镜的偏转实现激光束的水平方向扫描，经过X轴振镜的偏转扫描实现俯仰方向扫描，即可将激光束投影到工作面上，在待投影工作面上得到一定范围内的投影光斑。通过控制系统控制两振镜的偏转角度，可在待投影工件上形成三维激光束轮廓。最终实现在待投影工件上的1∶1精准投影，辅助指导工作人员进行零部件装配以及复合材料的多层铺贴等。

1.2 简化模型

激光3D投影系统进行投影定位时，系统内的双振镜扫描系统会根据CAD数模实现高精度偏转，通过X轴振镜和Y轴振镜的偏转将激光器发出的光束进行偏折，从而在待投影表面扫描出数模的轮廓。

激光3D投影系统的理论模型如图2所示，激光3D投影系统坐标系的建立：（1）以X轴振镜转轴为投影系统坐标系的X轴；（2）X轴振镜与Y轴振镜转轴中心连线方向为投影系统坐标系的Y轴；（3）根据右手定则确定Z轴方向，坐标系原点O为Y振镜转轴中心。其中θy为Y轴振镜的偏转角度，θx为X轴振镜的偏转角度，e为X轴振镜与Y轴振镜之间的异面距离。激光束偏转角分别为水平角V、俯仰角H，根据激光束偏转角与振镜转角关系可知水平角V=2θy，俯仰角H=2θx，则投影目标点P在投影坐标系下的坐标可由d、e、V、H表示为：

图2 简化模型

将式（1）写成矩阵形式：

由于双轴扫描振镜装置的驱动特性、电机的步距角等因素使得振镜偏转角θx、θy存在着误差，但X轴、Y轴振镜每次偏转引起的误差值并不固定，对应的投影点的误差也不固定，所以将其称之为动态误差。其各自误差为 Δθx、Δθy，式（3）给出了包含Δθx、Δθy误差的P点坐标：

式（4）给出了三维空间内任一点P的动态测量误差表达式。由式（1）可以看出P点的坐标是由d、θx、θy等参数的三角函数计算得到，三角函数关系的非线性导致扫描系统的扫描轨迹存在非线性误差。

1.3 复杂模型

以往，为了推导简化的激光3D投影系统的理论模型，进行如下假设：

（1）X轴、Y轴振镜的转轴垂直；

（2）入射光照射到Y轴振镜的转轴上中心；

（3）经Y轴振镜反射后的激光照射到X轴振镜的转轴上；

（4）与镜面的尺寸相比较而言，光线足够细。

但在实际情况中，激光器发出的光线不能严格满足假设（2）和（3），无法保证入射光准确地入射到Y轴振镜转轴中心，以及准确地入射到X轴振镜的转轴上，因此建立如图3所示的激光3D投影系统的复杂模型。建立如图所示的坐标系O-XYZ，假定入射光方向矢量为，Y 轴 振 镜 的 法 线 方 向 为，X 轴 振 镜 的 法 线 方 向 为，激 光 器 初 始 位 置 为，X 轴振镜中心为 O1=[0,e,0]＇，入射光线经Y轴振镜偏转后的方向矢量表示为：

图3 复杂模型

2 系统标定

激光3D投影系统的标定参数可以分为方向参数及位置参数两部分。方向参数标定指：投影坐标系和立体视觉坐标系之间的旋转矩阵R、入射光偏差以及驱动振镜转动时的角度偏差Δθx、Δθy。位置参数标定值指：投影坐标系与立体视觉坐标系之间的平移矩阵T以及激光器位置。其中，投影坐标系与立体视觉坐标系间的旋转矩阵R及平移矩阵T称为系统的外部参数，而入射光偏差、振镜转动偏差以及激光器位置偏差又称为激光3D投影系统的内部参数，这些参数的偏差都会对其定位精度产生影响。因此需对上述所提及的参数进行精确标定。

2.1 标定装置

标定所需用到的设备有：双相机、标定板、一维高精度平移导轨［9］。标定板置于一维高精度平移导轨上，使标定板垂直于高精度导轨的移动方向，保证标定板始终位于双相机的视野范围内。实验装置如图4所示。

图4 标定装置

2.2 标定方法

控制系统给定输入信号，控制X轴、Y轴振镜转动，使得振镜系统在扫描范围内的标定板上投影出一系列投影点。双相机拍摄标定板得到光斑图像，通过立体视觉算法计算得到投影点在立体视觉坐标系下的坐标值Pi(xi,yi,zi)(i=1,2,...,N)。保证双目立体视觉系统与激光3D投影系统的相对位置不变，移动标定板到k个位置使得Z=Zk(k=1,2,...,N)，重复拍摄并得到所有投影点的坐标值，采用最小二乘法对相同转角下的投影点拟合得到经二维振镜偏转后的出射光。出射光的拟合误差通过最小化式（10）来表示：

2.2.1 方向参数求解模型

激光3D投影系统方向参数求解模型是根据立体视觉坐标系下的出射光方向矢量与经过旋转矩阵R变换后振镜出射光方向矢量为同一方向矢量，建立对应关系，利用牛顿迭代法进行参数求解。

根据式（13），选用牛顿迭代法进行方向参数求解，F(x)=[f11,f21,f31,...,f1i,f2i,f3i]为牛顿迭代函数，根据迭代函数进行参数求解得到方程组：

图5 牛顿迭代法解算方向参数流程图

牛顿迭代法对迭代初值x0的要求比较严格，如果初值选择离根比较远，牛顿迭代法不一定能够收敛，初值选择不合适，会使得方程组的解不正确或算法不收敛，因此合理的初值选择对牛顿迭代法至关重要。本次实验的初值是根据振镜偏转角度与出射光夹角的关系来进行估值的，确保了初值的合理性。

2.2.2 位置参数求解模型

图6为粒子群算法解算位置参数的流程图，根据经验粒子群算法的参数选择如下：

图6 粒子群算法解算位置参数流程图

PSO：学习因子 c1=c2=1.5，权重 w=0.8，迭代次数10 000；

BreedPSO：学习因子c1=c2=2.0，权重w=0.7，迭代次数10 000；

2.3 标定模型误差评价

为了验证MATLAB参数求解精度，采用SA软件进行验证，将求解所得的数据导入SA中，采用同一目标点在立体视觉坐标系下与振镜坐标系下的点坐标差值的均方根值来表示，即转站误差值，用RMS表示。

整体的标定误差用所有目标点的均方根值来进行评价，表达式如下：

同时，也对旋转矩阵误差ΔR、平移矩阵误差ΔT进行如下定义，用公式表示为：

2.4 补偿方法

BP（back propagation）属于多层前馈神经网络，包含数据信息的前向传播与误差的反向传播。即计算误差从输入到输出的方向进行，如果实际输出与预期结果不符，则神经网络进入误差反向传播过程［11-13］。误差通过输出层传递，并根据误差梯度下降的方法逐层返回到隐含层和输入层，并将误差分摊到输入层和隐含层的各节点，进而更新各神经元的权重。重复上述训练步骤，直到神经网络的误差值低于目标。图7为BP神经网络模型图。

图7 BP神经网络模型图

模型精度评价：采用平均绝对误差（MAE）、平均相对误差（MRE）、均方根误差（RMSE）以及拟合优度（R2）对振镜转动角度的预测值与实际值进行比较分析。

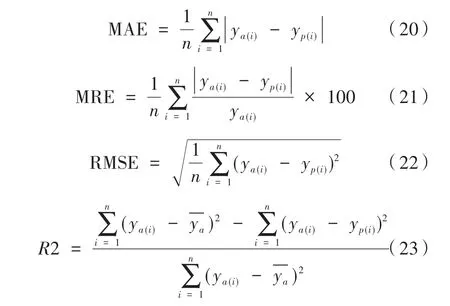
式中，ya(i)表示第i个振镜转动角度的实测值；yp(i)表示第i个振镜转动角度的预测值；表示振镜转动角的平均值；n为样本数据个数。

3 实验

3.1 仿真实验

为了验证本文求解方法的精度和稳定性，以及能够将解算结果与理论值相比较，从而能够对标定结果给出评价。根据激光3D投影系统的工作原理及其数学模型进行仿真实验。设定好激光3D投影系统的模型参数，并给定其与立体视觉坐标系间的转换关系，即给定二者间的旋转矩阵R、平移矩阵T。进行多次仿真实验，来验证参数求解方法稳定性及精度。

3.1.1 方向参数求解仿真实验

根据激光3D投影系统的工作原理以及给定的参数仿真得到目标点在立体视觉坐标系下的点坐标，并根据实际工作情况在这些目标点上施加服从正态分布的均值为0，方差分别为0.01 mm、0.02 mm、0.03 mm的噪声。并根据2.2所提到的最小二乘法进行出射光方向拟合。利用Newton迭代法以及LS法求解出振镜实际偏转角度值、入射光偏差值以及旋转矩阵R。出射光的方向矢量部分数据如表1所示。

表1 部分实验数据

根据2.2.1的数学模型对拟合得到的出射光利用LS与Newton迭代法求解出振镜实际转动角度，图 8为 varn=0、varn=0.01、varn=0.02、varn=0.03时的实际振镜转动角度值与理论转角的偏差值。

图8 解算结果

由图8比较可知LS算法求解转动角度在未加入噪声时的求解误差小于Newton迭代算法，同时可以看出，随着随机噪声加入的增大，对LS算法求解精度影响较大。

根据表2、表3可知LS算法对入射光偏差、旋转矩阵R的求解精度低于Newton迭代算法，LS算法求解旋转矩阵误差数量级在1×10-2°，Newton迭代算法求解旋转矩阵误差数量级在1×10-3°，结合上述内容来说，选择使用Newton迭代算法求解精度更高。对振镜转动角度的解算误差小于 6″。

表2 入射光Z向偏转0.5°LS、Newton迭代求解结果对比

表3 基于LS、Newton迭代求解旋转矩阵偏差ΔR对比

3.1.2 位置参数求解仿真实验

在第一步方向参数求解的基础上，利用方向参数的求解结果，采用PSO算法以及BreedPSO算法对激光3D投影系统的位置参数进行求解，即求解激光器位置参数S以及平移矩阵T。经过多次仿真实验，采用PSO算法与BreedPSO算法的平移矩阵求解误差在一个数量级，PSO的效果相对来说更好。利用PSO算法对激光器位置求解结果如表4所示。

表4 激光器位置参数（y、z）求解结果对比

为了观察目标点数对平移矩阵求解的影响，根据仿真得到的数据，分别取个数10～90的目标点进行目标点数对平移矩阵求解影响的仿真实验，对结果进行分析。根据图9可知，目标点数目在50个以上时，PSO算法收敛快且准确。

图9 目标点个数不同的PSO算法对平移矩阵的影响

表5为varn=0时的部分仿真数据，其中理论值代表立体视觉坐标系下的点坐标，实际值代表由求解得到的参数根据激光3D投影系统的数学模型求解得到的目标点的点坐标，dMag为两点的偏差值。根据表5可知单个目标点的解算误差不超过0.15 mm。

表5 部分仿真数据

在理论点坐标上施加服从正态分布的均值为0方差0.01、0.02、0.03的噪声来模拟立体视觉系统的实际工作情况，根据图10可以看出，该激光3D投影系统求解模型误差的RMS为0.1 mm，证明该求解模型的可行性与精确性。

图10 噪声不同的RMS误差结果比较

3.2 振镜转动角度补偿实验

本论文运用BP神经网络模型对振镜实际转动角度与理论转动角度进行建模探究其关系，以振镜实际转动角度作为输入，采用试错法对隐含层神经元数目进行调整确定，给定初始值，再逐渐增加其个数，通过BP神经网络训练结果，比较每次预测的精确度，来确定隐含层神经元个数最佳值。经过多次试验，得到当隐含层神经元个数为3时，误差控制在最小，因此本论文模型的最优节点数为3。

将振镜实际转动角度与理论转动角度的测量数据随机分为2组：三分之二的数据进行BP神经网络训练，三分之一的数据进行模型验证。输入变量个数为1，训练时隐含层神经元数从1增加到7，利用测试集中的精度评价及拟合优度来确定最优的隐含层神经元数目为3，如图11（a）。在此基础上，利用1-3-1结构的神经网络模型进行预测，得到预测结果如图11（b）所示。表明该模型的预测结果较好。表6为15次神经网络预测精度的平均值。通过计算可知对振镜转动角度的预测误差不超过5″。

图11 神经网络预测结果图

表6 神经网络模型精度评价

4 结论

阐述了激光3D投影系统的基本原理及其复杂模型，针对激光3D投影系统的复杂模型，提出了基于Newton迭代算法的方向参数求解以及基于PSO算法的位置参数求解方法。解决了方向参数求解算法初值选取的问题以及避免了位置参数求解的初值选取，同时得出激光3D投影系统中位置参数解算的最佳目标点数为70个。根据实际工作情况，在投影点坐标上施加均值为0，方差分别为 0.01、0.02、0.03的噪声后，进行仿真，仿真结果表明激光3D投影系统的振镜转动角度解算误差不超过6″，解算模型误差的RMS为0.1 mm，证明了基于Newton迭代法与PSO算法的优化算法的可行性。针对振镜存在转动偏差，提出了一种基于BP神经网络的误差补偿方法，通过多次仿真实验得到1-3-1结构的神经网络模型预测效果最好，其均方根误差小于5″，为后续激光3D投影系统的研究奠定了基础。