基于因果关系的人工智能
2022-11-15张勤
张勤
(1.清华大学 核能与新能源技术研究院,北京102202;2.清华大学 计算机系,北京100084)
1 引言
中国科协在2022 年6 月27 日召开的科协年会上发布了“2022 十大前沿科学问题”,其中第2个问题是:“如何实现可信可靠可解释人工智能技术路线和方案”[1]。科技部在“科技创新2030——‘新一代人工智能’重大项目2021 年度项目申报指南”中的第一章“新一代人工智能理论基础”中,将“因果推理与决策理论模型研究”列为第1.1 节的标题,要求“突破模型泛化瓶颈问题,提升模型系统的安全性、鲁棒性及可解释性”,“降低对数据独立同分布的依赖,提升泛化能力和可解释性”[2]。显然,当前流行的深度学习模型存在的泛化和不可解释等问题,导致了不可信、不可靠和鲁棒性等问题。科技部指南提出了“因果推理与决策”的技术路线,是对第一代基于知识的人工智能技术路线的某种回归,因为知识主要就是对事物间因果关系的描述。
但细观内容,科技部的指南仍然在数据驱动的框架内,因为指南中1.1 节的内容要求构建“数据驱动的因果网络结构学习理论”。网络的参数学习当然也是应有之义,但不是重点。这反映了科技部指南希望新一代人工智能既吸收第一代知识驱动的人工智能的优点,又保留第二代大数据深度学习优点的朴素想法。
2 因果贝叶斯网络
当前,最流行的因果网络结构学习模型是图灵奖获得者美国加利福亚尼大学洛杉矶分校的朱迪亚·珀尔教授创立的因果贝叶斯网络(Causal Bayesian Network,CBN)[3],即将贝叶斯网络(Bayesian Network,BN)[4]具体化为CBN。
BN 也是珀尔为主创立的,其定义为:
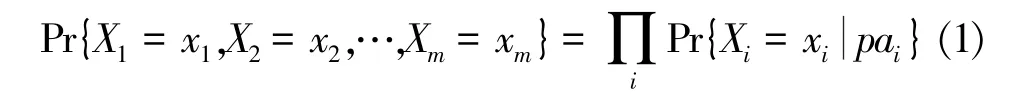
式(1)中,Pr{}是求概率的算符,Xi是网络节点变量,xi是Xi的一个取值或实例,pai是Xi的父变量取值的组合。实际上,是Xi的一个条件概率。在变量状态离散情况下,由Xi =xi和pai的各种取值构成的条件概率构成一个条件概率表(Conditional Probability Table,CPT),用以表达子变量Xi与其父变量(准确地说应该是条件变量)之间的条件概率关系。
在变量状态离散情况下,我们可以将Xi =xi简记为Xi,ji或Xiji,即Xi处于ji状态或取值。这样,式(1)可改写为式(2):
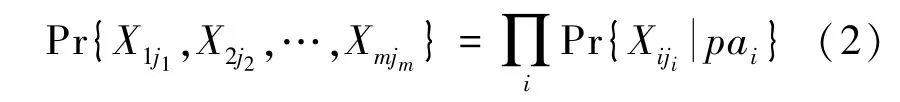
根据式(1)或式(2)对BN 的定义,BN/CBN 的结构必然是有向无环图(Directed Acyclic Graph,DAG),也就是说,BN/CBN 的结构不能出现有向有环图(Directed Cyclic Graph,DCG)。例如,图1 是基于DAG 的BN 示例图,图2 是DCG 示例图,是不被允许的(没有定义)。
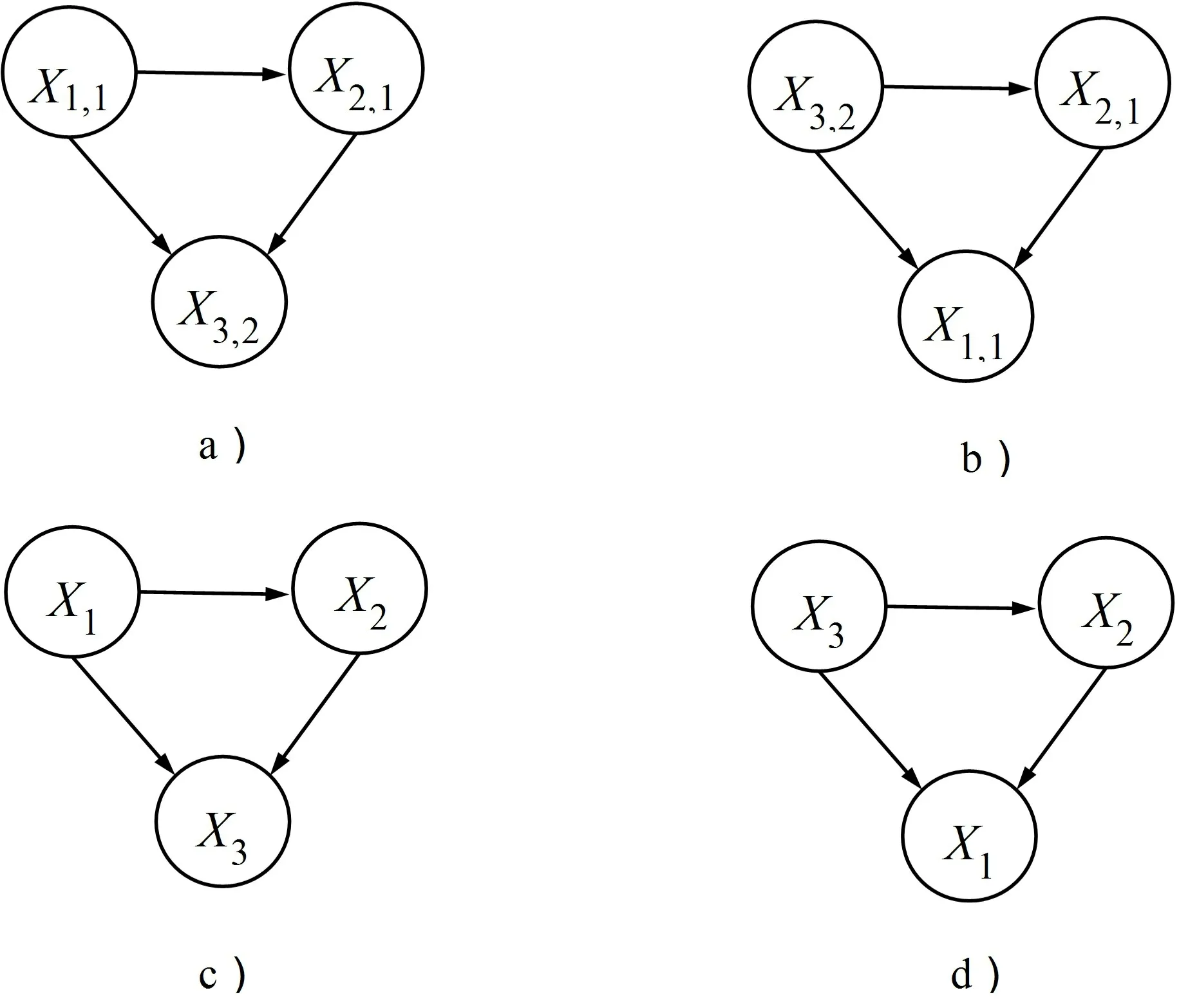
图1 基于DAG 的BN 示例
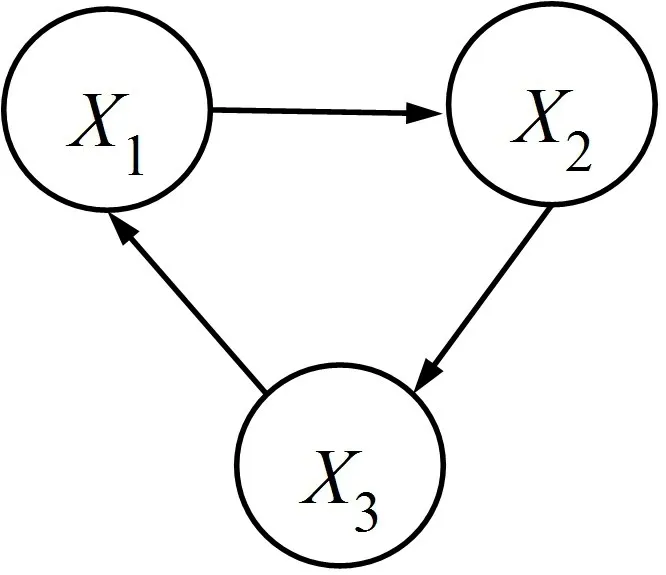
图2 DCG 示例
式(1)或式(2)表达了BN 中的节点变量的联合概率分布(Joint Probability Distribution,JPD),但节点的排序可以是任意的。例如:
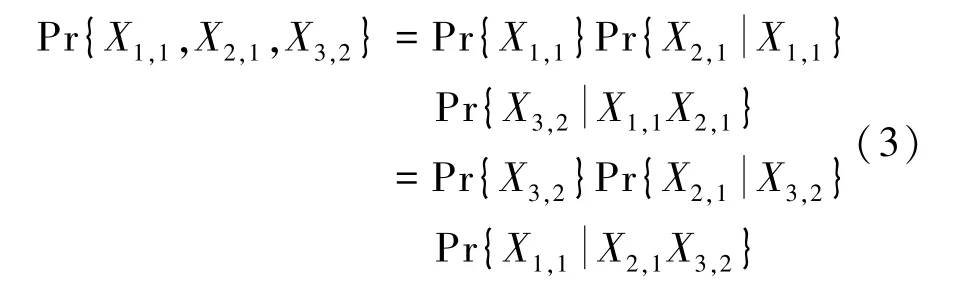
式(3)中的第一个等式可用图1a)表达,第二个等式可用图1b)表达。在不指定变量状态的情况下,图1a)成为图1c),图1b)成为图1d)。箭头指向为父变量→子变量。父变量与子变量之间的不确定性由CPT 表达。也就是说,同一个JPD 可以有不同但等价的BN。这说明BN 只是JPD 的因式分解表达,并不必然表达变量间的因果关系,从而难以表达知识、难以可解释。仅当BN 中的父节点是子节点的真正直接原因变量而非仅仅是条件变量时,BN 才成为CBN,才能表达变量间的因果关系,才具有可解释性。
要获得CBN,需要从反映JPD 的统计数据中学习CBN 的结构和参数[1]。这一过程通常被称为因果发现,其中需要通过存在于数据中的独立性和相关性并通过do 干预算子来确定变量间的因果关系。在有多个可能CBN 的情况下,用奥卡姆剃刀(最简化)原则和稳定性原则来选择最可能的CBN,且根据BN 的定义,CBN 不能有DCG。
3 因果贝叶斯网络的不足
尽管CBN 具有数学理论严谨等优点,但CBN也存在如下缺点,导致其难以普遍应用:
(1)对数据质量要求高(要体现各种独立性和相关性),数据获取难。
(2)从数据学出的因果结构未必符合领域专家的认知,从而难以被接受。
(3)用来选择候选结构的奥卡姆剃刀(最简化)和稳定性原则是经验原则,科学性不够。
(4)不适用于存在静态逻辑循环DCG 的情况,这是BN/CBN 的定义所决定的。
(5)因不允许DCG,无法通过模块化的方式构建CBN,导致构建模型困难和构建了也难以理解。
(6)父变量之间的逻辑关系隐藏在CPT 中(Implicit 表达)[5],可解释性不足,父变量间以及概率参数相互耦合(CPT 表达的是父变量的状态组合与子变量状态之间的条件概率)。
(7)难以利用领域专家已有的因果知识。
(8)计算复杂度高,计算效率低,难以用于大型复杂系统。
此外,其是否避免了数据独立同分布假设从而避免了泛化问题存疑。
一般来说,大型复杂系统的建模是一项艰巨的任务。理想的方法是模块化建模,即分别构建多个小的模块(局部),然后合成为完整模型(全局),这样可以以指数规模减少收集样本数据[4]。但这种方法很可能导致全局模型中出现DCG,这是BN/CBN 的定义所不允许的。例如,在不考虑气候因素的情况下,环境学者研究地表水X1减少的原因,发现植被覆盖率低X2和人类浪费水X5是主要原因(如图3a)所示),并进行了统计,得到了三者之间的CPT(X2、X5是X1的父变量);植物学者研究植被覆盖率低X2、土壤沙化X3和人类砍伐森林X4之间的关系(如图3b)所示),得到了三者之间的CPT;土壤学者研究土壤沙化X3、地表水缺乏X1和植被覆盖率低X2之间的关系(如图3c)所示),统计出了三者之间的CPT。将三个模块合成(相同变量合并),可得图3d),但其中存在DCG(X2→X3→X2;X1→X3→X2→X1)。根据BN/CBN 的定义,图3d)是无定义的。也就是说,BN/CBN 难以采用模块化的方式构建。
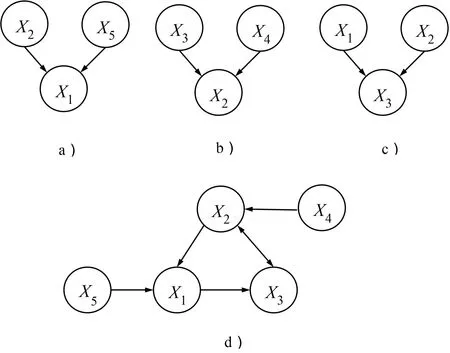
图3 模块化合成全局模型示例
4 动态不确定因果图
为克服BN/CBN 的不足,笔者及其团队创立了DUCG 理论[5~17],其基本思想是从因果关系的底层而非表象层表达和处理不确定因果关系。
所谓表象层,就是数据统计层面。例如BN/CBN 就是用统计得来的CPT 表达变量之间基于DAG 结构的因果关系的不确定性,既无法显式(Explicit)表达父变量之间的逻辑关系,也不允许DCG,各变量和参数相互耦合,难以模块化建模、难以动态和局部增删修改模型、难以高效推理计算。
所谓底层,就是父子间因果作用机理层。DUCG 用独立的虚拟因果作用随机事件变量P(用于单赋值DUCG:S-DUCG)或A(用于多赋值DUCG:M-DUCG)表达每个父变量对子变量的不确定因果作用机理,多个父变量对子变量的关系为简单逻辑或(S-DUCG)或者权重逻辑或(M-DUCG),复杂的关系由逻辑门变量G显式表达,并将G作为一个父变量对待。独立的P或A事件的发生概率表达因果关系的不确定性,这些独立事件及其概率的组合构成DUCG 的JPD 和CPT,从而将统计意义上耦合在一起的各个变量和参数解耦,进而在推理计算中引入逻辑化简(去掉与当前问题无关部分),引入由独立事件组成的因果链展开和逻辑运算,用矛盾律(结果不能同时是自己的原因)在因果链展开中解环,引入不确定证据算法、递归算法等,大幅提高计算效率和精准度,既可溯源,又可预测,也可反事实(Counterfactual)推理。其自动归一化定理保证了DUCG 可在不完备表达情况下精确推理。
所谓单赋值S-DUCG,是指子变量的一个状态(状态1)的原因被表达,另一个状态(状态0)只能是状态1 的补集,其原因不能被单独表达;所谓多赋值M-DUCG,是指子变量的任何一个状态的原因可以被单独表达。从数学上看,S-DUCG 完全满足概率论(集合论);M-DUCG 则有所突破,需要建立一个新的数学模型——权重集合论,来处理同一变量不同状态互斥(相关)和各状态原因独立表达之间的矛盾。两者可以混合,统称为DUCG(详见文献[7]和[8])。
图4 是与图3 对应的M-DUCG,其中根原因变量用字母B表达,独立的虚拟因果作用随机事件变量用加粗有向弧表达,以区别于BN/CBN。注意,DUCG 允许DCG,使得模块化构建DUCG 成为可能。如何用图3a)、b)和c)的局部统计数据构建图4d)那样的全局DUCG、JPD 和CPT,进而定义和计算图3d)的带DCG 的BN/CBN,参见文献[6]和[17]。
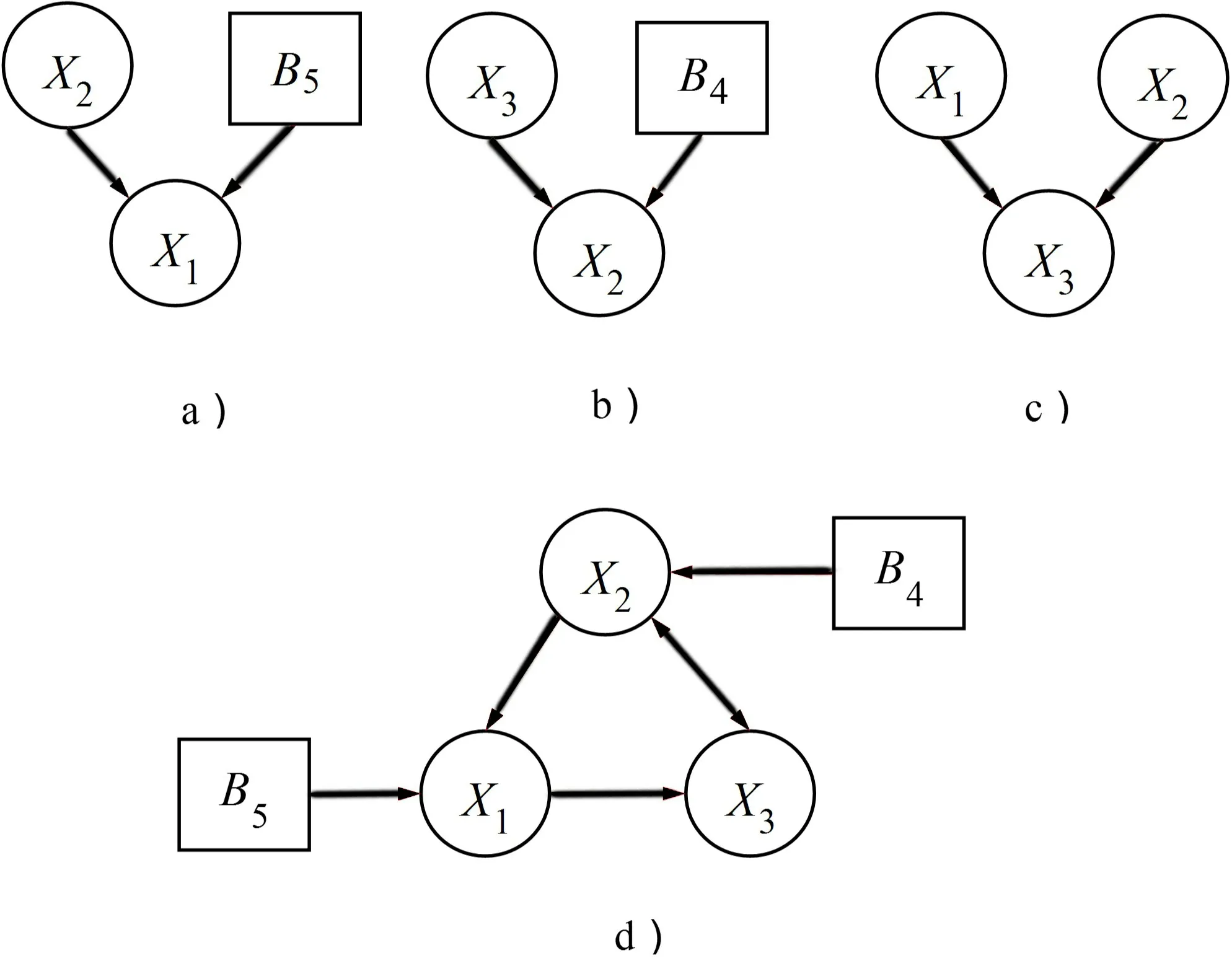
图4 模块化合成全局M-DUCG 的示例
模块化建模的优势明显:除每个局部(模块)可解释性强、可随时通过修改局部而重构全局模型外,还可显著降低统计数据的收集量和难度。例如一个包含20 个模块的系统,每个模块有10 个变量,去重后共计100 个变量,每个变量有2 个状态。按照100 个变量状态的每个组合收集10 个样本计,共需收集2100×10 =1.267×1031个样本。如果采用模块化方式建模和收集样本,按照相同的标准,仅需收集20×210×10 =2.048×105个样本。
图5 是M-DUCG 的数学模型(S-DUCG 类似,参见文献[7])。
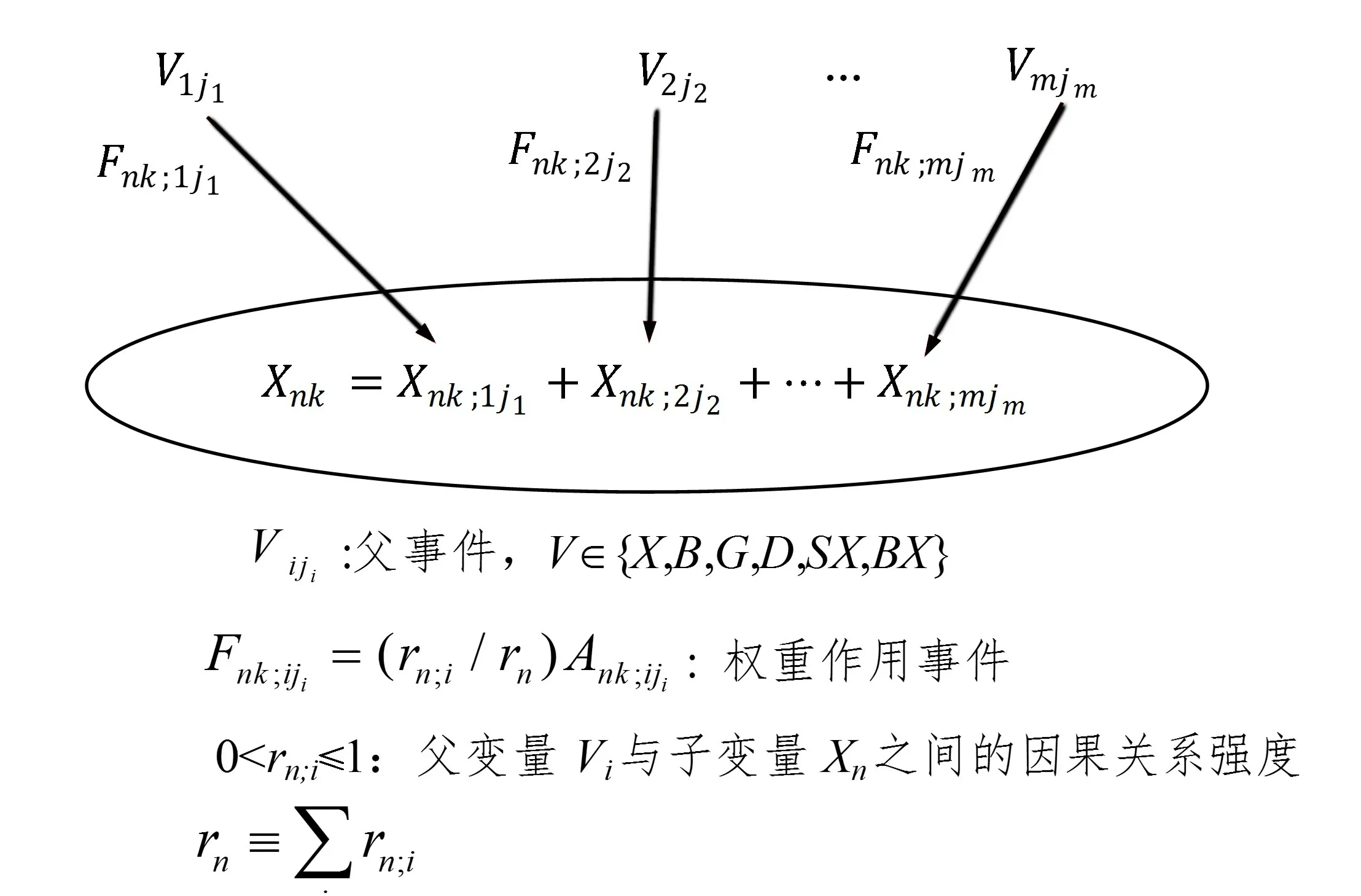
图5 M-DUCG 模型
其中,D是缺省原因(或未知原因)事件,SX是特异性(金标准)子事件变量,BX是集成或受风险因素影响后的B变量;Ank;iji是父事件Viji导致子事件Xnk发生(即Xnk;iji发生)的独立的虚拟因果作用随机事件,其发生概率ank;iji =Pr{Ank;iji}表达Viji导致Xnk发生的不确定性;rn;i表达Vi与Xn之间是否存在因果关系的不确定性。“+”是权重逻辑或算符,其作用与互斥或EOR 相似,但含义不同。Fnk;iji是权重虚拟因果作用随机事件,Pr{Xnk;iji}=Pr{Fnk;ijiViji} 是Viji对Xnk发生的概率的贡献。
用公式表达M-DUCG,就是式(4):
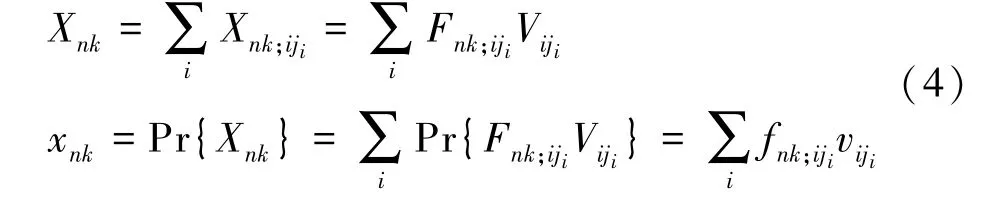
如果V =X,可重复使用式(4),直到V∈{B,D} 。
作为一个原创的理论体系,DUCG 还有很多内容,不在此一一介绍。有兴趣的读者可参阅文献[15]~[17]。
目前DUCG 已在大型复杂工业系统故障监测、预报、诊断、发展预测、决策支持、安全评价、临床辅助诊断等领域投入实际应用。以全科临床诊断为例,已覆盖发热、腹痛等43 个主诉症状、每个主诉含跨科室的数十到上百个疾病,去重后覆盖1 400多个疾病、10 000 多个ICD-10 疾病代码,在基层医院实际诊病已逾30 万例,只在早期出现过8 例诊断错误(已纠正无再错),具有天然的可解释性,算法透明,无泛化问题,安全可靠鲁棒,还能精确推荐下一步该做的检查,动态生成患者个体优化临床路径,显著节省检查费用。
5 结束语
如珀尔所述[18],因果关系是打开可信人工智能的钥匙。当然,笔者认为基于因果关系的可信人工智能未必是全能的。只要能够可信地解决应用领域的实际问题,包括可解释性和泛化问题,就实现了新一代人工智能的初衷。
