因果作用评价与因果关系发现

英乃文 苗旺 耿直

（1.北京大学 数学科学学院，北京100871 ；2.北京工商大学 数学与统计学院，北京100048）

1 引言

因果关系是推动重大科学发现的关键，深度挖掘因果作用的机制更是科学研究所寻求的“可解释性”的重要一环。因果推断是利用数据评价变量之间因果作用、学习因果关系的统计理论和方法。近年来，有关因果推断的理论、方法和应用的研究成果多次获得了诺贝尔经济学奖和图灵奖。大数据和人工智能研究向因果推断提出了越来越多的挑战性问题，因果推断已成为人工智能领域有关不确定性推理的关键研究方向之一。现代大数据为因果推断提供了丰富的应用场景，人们需要一场“因果革命”来推动科学发现与应用技术的发展，而非单纯地从事物之间相关性的角度进行科学研究。利用随机试验设计可以有效地评估因果作用［1］。在医学中，随机化试验被视为评价药物有效性和安全性的“金标准”。在社会科学中，随机化试验也有越来越广泛的应用，例如，阿比吉特·巴纳吉、埃丝特·迪弗洛和迈克尔·克雷默使用随机化试验研究发展中国家的教育问题和贫困问题［2］，相关的研究成果获得了2019 年诺贝尔经济学奖。在许多实际问题中，由于成本、伦理问题等限制，无法开展随机化试验，只能使用观察性研究得到的数据探索因果问题。观察性研究中必须考虑存在那些可能的协变量，它们既与暴露因素（或接受的处理）相关，又与结果变量相关，这些协变量称为混杂因素（Confounders）。例如，在研究教育程度对收入的影响时，家庭背景和社会环境等变量都是重要的混杂因素。混杂因素导致处理组和对照组个体存在差异，导致观察数据中的相关性和真正的因果作用有偏差，这是观察性研究的核心难题。刻画混杂因素问题的著名例子是Yule-Simpson 悖论——处理和结果的相关性会由于调整混杂因素而发生改变或逆转。更具有挑战性的是，在现代很多大数据研究中并不存在合理的对照组。大数据的一个重要来源是关于某一区域或群体的长时间、多维度的宏观数据，例如，每个城市多年以来每天的出生、患病、死亡人数等数据。在这些宏观数据中，人们关心的是在某一群体里施行的宏观干预措施的作用，例如，在传染病疫情防控中，评价对疫情严重城市采取的防控措施是否有效。是否能找到恰当的对照是观察性研究的关键，如何科学地评价无合理对照研究中的因果作用更加具有挑战性。

科学研究不仅关心因果作用大小，进一步，还需要关心因果作用的机制。例如，关于吸烟和肺癌的研究，人们不仅关心吸烟是否导致肺癌，还关心吸烟是否通过血压、肺部尼古丁含量等中间变量引起肺癌。因果网络学习是挖掘多个变量之间因果机制的因果推断方法，但是因果网络的结构通常不能由数据唯一确定，而只能得到一些网络的Markov等价类，同一等价类中的因果关系和混杂结构不完全相同，这为多变量之间的因果关系学习和因果作用评价带来挑战。因果推断的另一个研究内容是反事实归因。例如，一位在石棉工厂工作的60 岁工人得了肺癌，他患肺癌由石棉引起的概率有多大。这是一个反事实推理，需要想象：“假若该工人没有在石棉厂工作，是否就不会患肺癌？”法庭上利用证据如何归因和量刑，如何根据一个人出现的各种症状和医学检查结果进行疾病诊断，一个系统不能正常工作，更可能是由于哪个部件发生了故障等，都需要进行归因分析。但目前常用的方法都是基于贝叶斯条件概率和相关性的统计方法，缺乏基于因果关系的归因分析方法。大数据时代，数据驱动及统计学理论支撑的定量化归因方法将会越来越重要。

2 因果模型与因果作用的定义

潜在结果模型由内曼［3］在设计农业随机试验比较不同作物品种的产量时引入，并由鲁宾［4］进一步延拓到观察性研究中。潜在结果模型能够直接和清晰地定义因果作用和表述因果假定，目前已经在统计学、流行病学以及社会科学研究中得到了广泛的认可。用X表示一个处理或暴露变量，Y表示观察到的结果变量，用Yx表示个体如果接受处理X ＝x后的结果，称为潜在结果（Potential Outcome）。潜在结果模型一般需要个体处理值稳定假定：每个个体的潜在结果不受其他个体处理的影响，且每个个体在每一种处理下只有一个潜在结果；还需要一致性假定［5］：当X ＝x时，Y ＝Yx。对任意两种不同的处理水平x和x＇，可以通过潜在结果之差定义处理对结果的因果作用。为了研究某种处理的影响，人们常常关心处理在所研究总体上的平均因果作用（Average Causal Effect，ACE）：

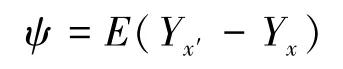
通常考虑一个二值变量（X＝1 或0）的因果作用。因果推断的核心目标是识别和估计因果作用，识别性是指感兴趣的因果作用能够从观测数据分布中唯一决定。由于对每个个体，潜在结果｛Y1，Y0｝ 不能同时观测到，为了识别因果作用通常需要额外的假定。

珀尔借助有向无环图（Directed Acyclic Graph，DAG）表示变量间的因果关系［6］，用do 算子形式化定义因果概念，根据图结构建立因果作用的识别和估计理论，建立了因果图模型。这项工作获得了2011 年的图灵奖。一个因果图中的每个节点表示一个变量，节点之间的有向边表示由原因到结果的因果关系，一个没有环的有向图称为有向无环图。对于一组可观测的变量X1，X2，…，Xn，用pai表示变量Xi的父节点变量的集合。每个节点的取值由它的父节点pai和随机误差εi的函数确定Xi ＝fi（pai，εi）。给定一个有向无环图，那么（X1，…，Xn）的联合概率分布为：

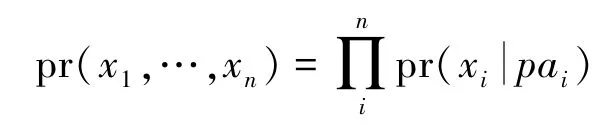
珀尔使用do 算子表示外部干预。对某个变量用do（Xi ＝x＇i）表示强制设定其值为x＇i，即，删除指向被干预变量的所有有向边，并将该变量的值设置为x＇i。干预后的联合分布变为：

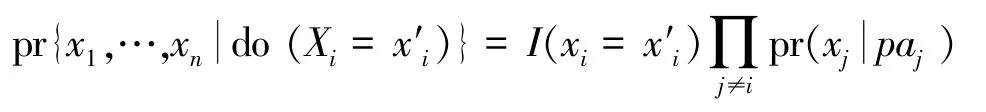
其中，I（·）为示性函数。特别地，原因X对结果Y的因果作用为。与条件概率不同，do 算子使用外部干预X ＝x下Y的分布形式化定义了X对Y的因果作用，与潜在结果模型定义的因果作用具有等价性［7，8］。

3 代理推断

3.1 平均因果作用的代理推断

当混杂因素可观测时，罗森鲍姆和鲁宾［9］提出的可忽略性假定和倾向得分是调整混杂因素和识别因果作用的最重要工具。如果所有混杂因素都被观测到，那么条件在混杂因素的每一层上，处理可以看作随机分配的，因此因果作用可识别。在可忽略性假定下，匹配、逆概率加权估计、回归等方法已广泛用于因果作用的估计。但是，如果存在未观测的混杂因素，可忽略性假定不成立，因果作用不可识别。工具变量方法［10，11］是调整未观测混杂因素的一种重要方法，在社会经济和生物医学中有广泛应用，Angrist 和Imbens 因为工具变量方法方面的工作获得了2021 年诺贝尔经济学奖，但是该方法需要较强假定，弱工具变量或无效工具变量仍然会导致因果推断的偏差。最近研究者提出和发展了代理推断方法［12～15］，该方法有效利用观察性数据中存在的混杂代理变量做混杂因素调整，识别因果作用，已被用于平均因果作用的推断、纵向研究、合成对照、测试-阴性研究中。以下我们简要回顾代理推断方面的研究。

代理推断（Proximal Inference）方法是文献［12］提出的处理未观测混杂因素的方法，其原理是在一定条件下，观测到的协变量可以作为未观测混杂因素的代理变量（Proxies），进而可消除混杂因素导致的偏差并识别因果作用。用U表示未观测的混杂因素，我们把观测到的协变量分为三类：①处理变量和结果变量的共同原因V；②处理诱导的混杂代理变量（Treatment-inducing Confounding Proxies）Z；③结果诱导的混杂代理变量（Outcome-inducing Confounding Proxies）W，这三类协变量满足如下条件。下面用表示给定U条件下X与Y独立。

假定3.1（潜在可忽略性）：；对任意x，，f是概率密度函数。

假定3.2（混杂代理）：；。

假定3.3（结果混杂桥函数）：存在函数h，对所有x均有：

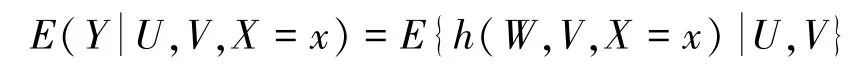
假定3.4（处理混杂桥函数）：存在函数q，对所有x均有：

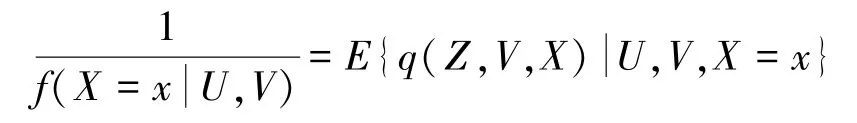
假定3.5（完备性）：

（1）对任 意v，x及所有平方可积函数g，，V ＝v，X ＝x｝＝0 当且仅当g ＝0。

（2）对任 意v，x及所有平方可积函数g，，V ＝v，X ＝x｝＝0 当且仅当g ＝0。

（3）对任 意v，x及所有平方可积函数g，，V ＝v，X ＝x｝＝0 当且仅当g ＝0。

（4）对任 意v，x及所有平方可积函 数g，，V ＝v，X ＝x｝＝0 当且仅当g ＝0。

假定3.1 表示U包含了影响X和Y的所有未观测混杂因素，且处理组和对照组人群有充分的重叠。在这个假定下，有，U，V）｝，但是，由于U未观测，无法直接从观测数据中计算E（Yx）。假定3.2 刻画了混杂代理变量满足的条件，要求Z对（W，Y）没有直接因果作用，X对W没有直接因果作用，而在观测数据中，Z和（W，Y）以及X和W的关联性完全由混杂因素U导致。这样的混杂代理变量在流行病学中也称为阴性对照变量，Z称为阴性对照暴露（Negative Control Exposure），W称为阴性对照结果（Negative Control Outcome）。阴性对照或混杂代理的例子在实际研究中经常存在，例如，在空气污染对死亡率影响的时间序列研究中，未来的空气污染水平可以作为阴性对照暴露，过去的死亡率可以作为阴性对照结果［16，17］。工具变量可以看作阴性对照暴露的特例。在流行病学研究中，阴性对照变量曾被用于检验混杂因素是否存在，但通常需要较强的模型假定［16，18］。假定3.3 引入混杂桥函数（Confounding Bridge Function）h刻画U对Y和W的混杂作用的关系，类似地，假定3.4 使用混杂桥函数q刻画U对X和Z的混杂作用的关系。混杂桥函数是代理推断的一个关键概念，实际上刻画的不仅是混杂作用之间的关系，还代表了变量之间因果作用，以及观测到的关联性之间的关系。混杂桥函数不需要已知，可以从观测数据识别。

定理3.1［12，15］

（1）在假定3.1～3.3 下，有：

在假定3.5（1）也成立时，E（Yx）可由任意满足式（1）的函数h识别，即：

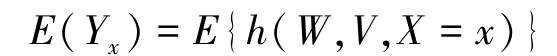
（2）在假定3.1～3.2 和假定3.4 下，有：

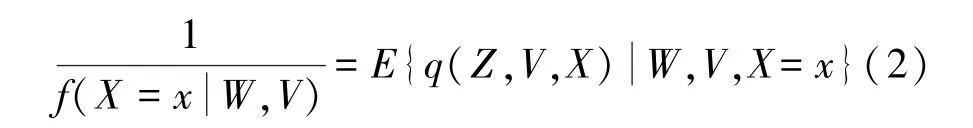
在假定3.5（2）也成立时，E（Yx）可由任意满足式（2）的函数q识别，即：

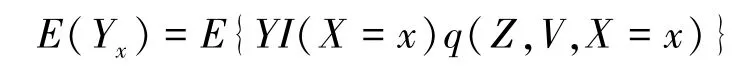
其中，I（X ＝x）是示性函数。

定理3.1 表明混杂桥函数也刻画了观测数据之间由于混杂因素导致的虚假相关性，可以使用观测数据解方程（1）和（2）得到混杂桥函数h和q，然后识别潜在结果期望或因果作用。定理3.1 并不需要h和q的唯一性，方程（1）和（2）的所有解都可以识别平均因果作用。特别地，在假定3.5（3）（4）也成立时，混杂桥函数h和q可由观测数据唯一确定。完备性假定是识别性问题中常见的假定，许多常用的参数或半参数模型满足完备性条件，如指数族分布［19］。非参数模型中的完备性条件可参见文献［20］。在代理推断问题中，完备性假定在离散和连续情形有相应解释［15］。

定理3.1 对观测数据的分布没有约束，但在实际问题中，可以对混杂桥函数指定一个参数模型，利用广义矩等方法估计混杂桥函数，然后估计因果作用。在一定正则条件下可以证明相合性和渐近正态性。文献［13］［15］进一步建立了代理推断的半参数理论和双稳健估计。

3.2 合成对照的代理推断

在一些观察性研究中，研究目标是考察干预措施对大型的实体的因果作用，例如，提高烟草税收对某个国家或地区烟草消费的影响，东德西德合并对西德经济发展的影响。在这类研究中，往往只有一个个体接受处理，而作为对照的个体都与接受处理的个体有较大差异，由于时间趋势的影响，接受处理的个体在处理前后的差异并不等同于因果作用。这种比较案例研究在政治学、公共卫生和经济学等多个领域有重要应用。

为了消除混杂因素和时间趋势的影响，文献［21］使用合成对照（Synthetic Control）方法，将多个对照个体加权组合成一个新的虚拟对照，用来近似处理个体假如没有接受处理的状态，基于处理个体与合成对照的比较评价干预措施对处理个体的因果作用。假定数据由个体i ＝0，1，…，N在t ＝1，…，T共T个时期上的观测组成，令Y（t）和W（it）分别表示处理组个体和编号为i的对照个体在时间t的观测结果，处理施加在时间T0和T0+1 之间，只有个体i ＝0 接受处理，编号i ＝1，…，N的个体属于对照组。令X（t）表示个体i ＝0 在时间t接受处理的状态，用｛Y1（t），Y0（t）｝ 和｛W1（it），W0（it）｝ 表示相应的潜在结果。

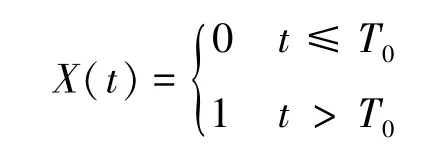
使用一组权重｛αi｝ 给对照组加权，并用∑αiW（it）近似Y0（t），从而用Y（t）-∑αiW（it）估计处理在时刻t对个体i ＝0 的因果作用。

估计权重｛αi｝ 是合成对照的关键，文献［21］使用处理前数据Y（t）对W（it）做回归估计权重。但这一方法已被指出是有偏的［22］。文献［23］提出了合成权重的代理推断估计，在如下的假定下，该方法能得到权重的相合估计。

假定3.6（交互固定效应模型）：对任意t有：

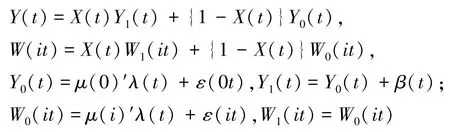
其中，β（t）是未知的随时间变化的因果作用；λ（t）是未观测混杂因素，μ（i）是未知的混杂作用；ε（it），i ＝0，…，N，t ＝1，…，T是随机误差项，满足

假定3.7（合成对照的存在性）：给定对照组的一个子集D，存在一组权重αi（i∈D）使得μ（0）＝

假定3.8（对照个体无干涉）：令Z（t）＝｛W（jt），j∉D｝，W（t）＝｛W（it），i∈D｝，满足，X（t）＝0｝，t ＝1，…，T0。

假定3.9（完备性）：对所有平方可积函数g和任意t≤T0，，Z（t）｝＝0 当且仅当g ＝0。

假定3.6 是合成对照问题中常用的模型，由于未观测混杂因素λ（t）的存在，接受处理的个体i ＝0 的结果在处理前后的差同时包含处理因果作用和混杂作用。而由于混杂因素对不同个体的作用不同，使用单个对照个体无法消除混杂作用。但在假定3.7 下，可以使用对照组的一个子集，通过加权构造出一个虚拟对照，混杂因素对该虚拟对照和处理个体有相同的作用，因此可以用来消除混杂作用。合成对照的关键在于识别合成权重｛αi｝ 。可以把W（t）看作结果诱导的混杂代理，而在对照组中，除了用作合成对照的子集D，对照组的其他不参与合成对照的个体Z（t）同样受到混杂因素的作用，但是假定Z（t）和W（t）之间互相没有直接影响，即假定3.8，那么其余个体的观测结果Z（t）可看作处理诱导的混杂代理。根据合成对照的存在性，可以把看作是混杂桥函数，因而可以使用代理推断的方法识别合成权重｛αi｝ 。

定理3.2：在假定3.6～3.9 下，对任意t有。其中，αi（i∈D）是方程，Z（t）｝＝0，t≤T0的唯一解。即，αi（i∈D）可识别。

利用观测数据样本，可以采用广义矩方法估计合成权重和进一步估计因果作用。此外，文献［23］还建立了非参数合成对照模型的识别与估计。

除了平均因果作用评价与合成对照，代理推断在生物医学、公共卫生和社会经济领域得到快速发展和应用。例如空气污染对健康影响的研究［17，24］；电子病历数据和疫苗安全性评价［14］等等。文献［13］［25］最近将代理推断方法推广到更为复杂的纵向数据研究中，其中处理、协变量和未观测的混杂因素都是随时间变化的，且过去接受的处理会影响观测或未观测的时变协变量。其识别性和半参数估计理论可以平行地建立。文献［26］将代理推断应用于测试-阴性研究（Test-negative Design，TND）。测试-阴性研究是实践中评价传染病疫苗有效性的一种重要方法。该方法将有相关症状并寻求治疗的疑似病例纳入研究，通过实验室检测确认他们是否被感染，通过比较检测阳性和检测阴性的两组人群的疫苗接种率来评价疫苗有效性。但是这种方法容易受到混杂因素和选择偏差的影响，论文建立了可以同时调整混杂和选择偏差的代理推断方法，并应用其评价多个新冠疫苗的有效性。

4 因果网络学习与因果作用评价结合的方法

传统的预测方法，不论是统计方法还是机器学习方法，都不需要确定各个变量在因果机制中的位置，只要利用更多的变量能提高预测精度就可以了。但是，在因果推断和决策时，需要确定各个变量在因果机制中的地位。评价因果作用时，通常需要已知观测变量之间的因果关系。例如正确区分混杂因素和处理与结果变量相关的中间变量。在实际应用中，如果不能正确判断混杂因素与中间变量，可能会导致错误地评价因果作用。下面以吸烟X与肺癌Y为例，假设还观测了第三个二值变量Z，得到表1 的观测数据。分析该数据需要了解变量Z是混杂因素，还是中间变量。

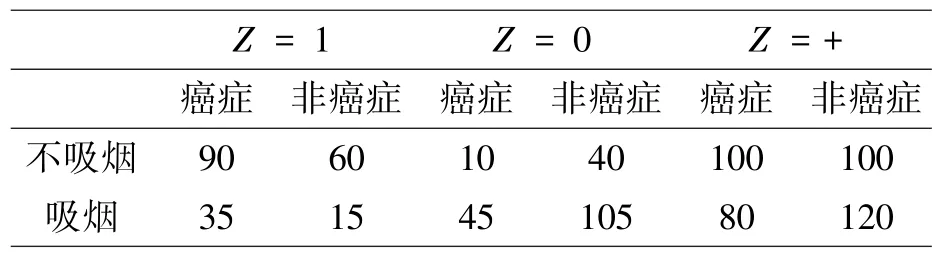
表1 吸烟与肺癌及第三个变量Z 人数观测数据

如果把变量Z当作混杂因素，例如性别（图1a）），应对它分层分析，得到吸烟对肺癌有正的平均因果作用：

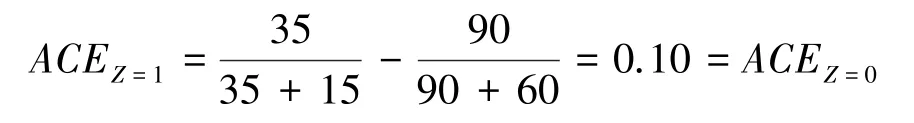
如果把变量Z当作中间变量，例如肺中烟油量（图1b）），那么不应分层，正确的吸烟对肺癌的总平均因果作用应该是负的：

图1 吸烟与肺癌及第三个变量Z

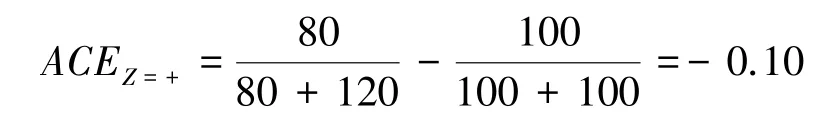
当观测数据包含很多变量，且它们之间的因果关系未知，可以利用数据先确定变量之间的因果关系。下面我们探讨因果网络学习与因果作用评价结合的方法。首先，利用数据进行因果网络学习，通常不能确定唯一的因果网络，而是得到Markov等价类，包括若干个因果网络，不能仅利用数据进一步区别某些变量之间的因果关系。图2a）为一个生成观测数据的因果网络DAG。利用因果网络结构学习方法可以得到图2b）所示的CPDAG，其中有3 条无向边，要求不能构成有向环或新的V-结构，它们的箭头方向共6 种组合，对应Markov 等价类的6 个因果网络。

然后，针对等价类中每个因果网络，确定处理变量X的父节点集合pa（X）和结果变量Y的父节点集合pa（Y）。6 个因果网络中，有4 种可能的（pa（X），pa（Y））对：

最后，根据得到的（pa（X），pa（Y））对，评价X对Y的总因果作用和直接因果作用。评价总因果作用（Total Effect）时，将pa（X）作为混杂因素：

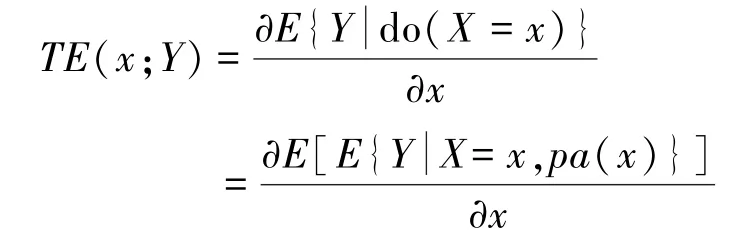
评价直接因果作用（Direct Effect），将Z ＝pa（Y）＼｛X｝ 作为混杂因素，切断X到Y其他路径：

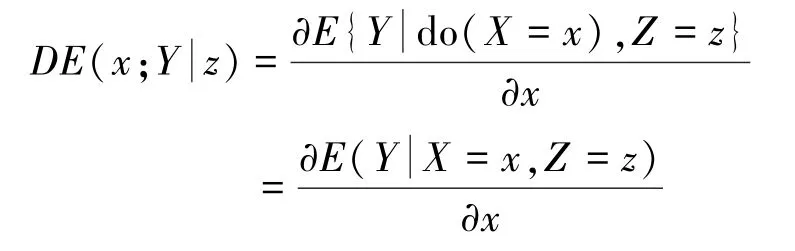
注意不能引入新的混杂，例如，在X→Z1←Z2→Y中，不能用Z ＝｛Z1｝ 。假定图2a）中的因果网络表示的是线性的因果结构方程：

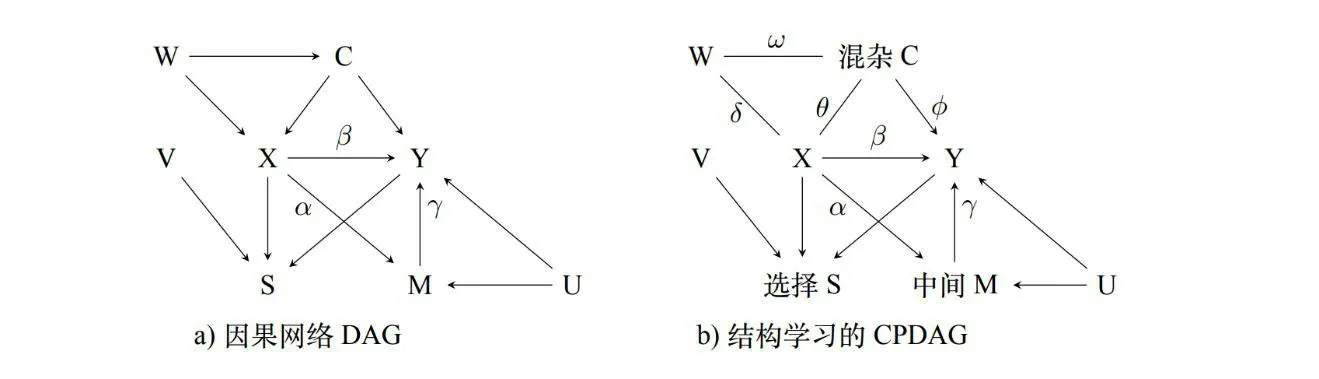
图2 因果网络与Markov 等价类

其中，总因果作用为TE ＝α1，直接因果作用为DE ＝β1。那么，等价类中6 个因果网络的所有可能的X对Y的总因果作用有4 个：

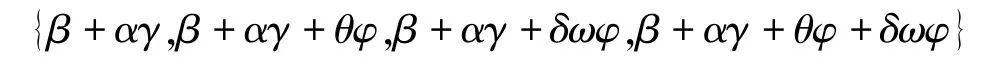
这个集合包含真的总因果作用即β+αγ，但从数据无法确定哪个是真。直接因果作用可以唯一确定，即β。

对于高维变量，学习完整的因果网络是非常困难的。但仅为了评价处理变量X对结果变量Y的因果作用，没有必要学习完整的因果网络，只需要学习处理变量X和结果变量Y的父节点对（pa（X），pa（Y））。利用文献［27］提出的因果网络局部学习的MB-by-MB 算法，文献［28］提出了局部因果网络学习与因果作用评价的结合方法，可以避免学习完整的因果网络。

5 基于因果推断的归因方法

珀尔提出了人工智能因果推断的三个层级：基于相关性的预测、基于因果作用的决策、基于反事实的归因。并指出当今大多数机器学习方法属于第一层级基于相关性的预测。近年来，因果推断受到了越来越多的关注，绝大多数方法是关于第二层级的因果作用（Effect of Cause）的研究，即评价干预决策有什么效果。例如，某种治疗方法是否有效、某种暴露环境是否有致病危险。关于第三个层级的反事实归因问题的研究还很少。反事实归因的问题是如何评价结果的原因（Cause of Effect）。例如，图3 描绘了儿童白血病与危险因素的因果网络。某儿童患了白血病，已知装修过房间、接触过油漆涂料、不爱吃蔬菜和水果。他患白血病应该归因于其中哪一项。在法律、环境、人工智能、生命科学等多个领域利用归因发现结果的原因都有非常重要的意义。

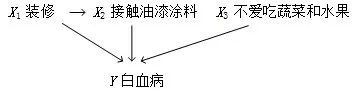
图3 儿童白血病的危险因素：家里装修、接触油漆涂料、不爱吃蔬菜和水果

目前，大多数归因方法是基于相关性或贝叶斯条件概率的方法。下面简要说明根据相关性、贝叶斯概率和因果作用进行归因的问题。归因是关于由某个个体的结果发现其原因的问题，既需要考虑因果作用，又需要考虑先验概率和条件概率。

首先，讨论概率专家系统根据条件概率推断原因的可能出现的问题。给定Y ＝1 条件下，计算Xk＝1 的后验概率：

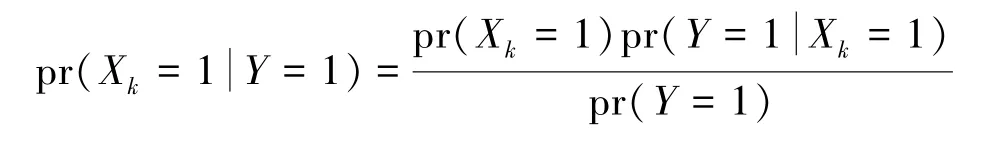
其与先验概率pr（Xk ＝1）有关，而Xk不一定会导致Y ＝1。例如，图4 描述了高血压的因果网络。尽管胸痛X3不是高血压Y的原因，但出现高血压Y ＝1时，胸痛X3＝1 的条件概率可能会比高血压的原因（不运动、心脏病）的条件概率都大：

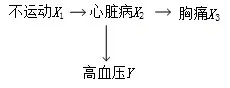
图4 高血压的因果网络

而ACE（X3→Y）＝0＜ ACE（X1→Y）和ACE（X2→Y）。贝叶斯条件概率的推理依赖于先验概率，某事件的先验概率大会导致其后验概率较大，但没有事件之间的因果关系。

其次，讨论根据因果作用来推断事件的原因可能出现的问题。例如，污染食品与毒药都可能致死。毒药X1致命的因果作用比污染商品X2致命的因果作用大很多。当一个人死亡Y ＝1 时，在没有是否服毒的证据时，不能将死亡归因于服毒X1，因为服毒的先验概率很小。基于因果作用的原因推断不考虑原因事件的先验概率。

目前，统计学和机器学习领域已有很多评价因果作用的方法，但关于事件归因的研究却未得到应有的重视。有少数学者探讨了如何定义结果事件的原因的问题。18 世纪哲学家休谟，以及后来的刘易斯［29］描述了因果关系的反事实定义：假若当初事件X没出现，则随后的事件Y就不会出现，那么事件X是事件Y的原因。珀尔［30］形式化定义了反事实因果概率：

其中，“1”表示事件出现，“0”表示事件未出现。并定义了如下的必要原因的概率（Probability of Necessity）。

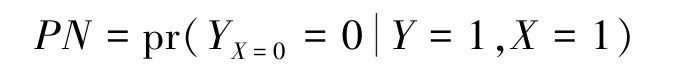
在对处理或暴露X进行随机试验的情况，即时，

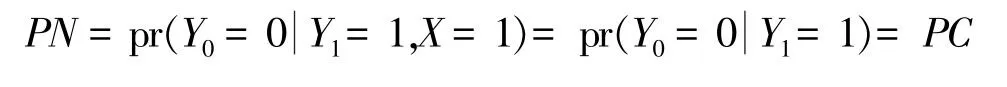
原因的概率PC和PN的可识别性比因果作用的可识别性需要更强的条件，即使是随机化试验和无混杂因素的情况，原因的概率也不可识别，只能得到其上下界。文献［31］给出了PC的下界：

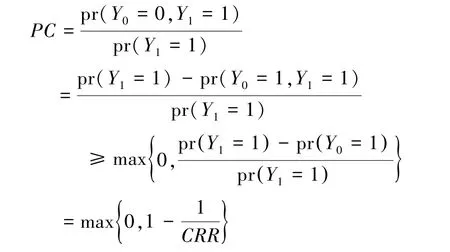
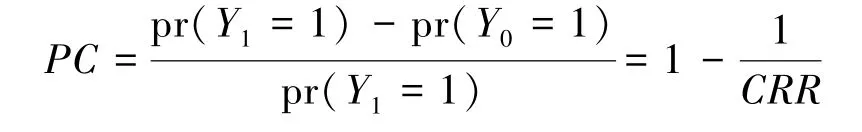
文献［32］将某个个体出现的结果事件和暴露因素作为证据（X ＝x，Y ＝1），定义了给定证据下处理X对结果Y的后验因果作用：

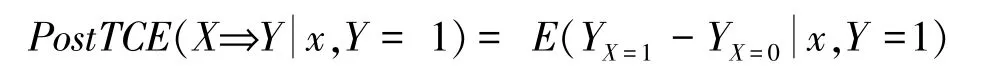
当证据为（x ＝1，Y ＝1）时，Y ＝1）＝PN。

后验因果作用将如何评价结果的原因看为已知证据下的评价因果作用的问题。给定证据为（Y＝1）时，处理X对结果Y的后验因果作用为：

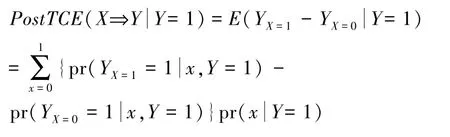
文献［32］进一步提出了多个危险因素对结果变量的后验因果作用的定义。令Y为二值结果变量，X ＝（X1，…，Xp）为p个二值原因变量，满足因果排序，即Xj不是Xi的原因（i ＜ j）。记X-k ＝X＼｛Xk｝，X ＝（Ak，Xk，Dk）。令x ＝（x1，…，xp）x＇＝（x＇1，…，x＇p）表示xi≤x＇i，对任意i。给定证据E＝e，其中变量集合E为变量X和Y的子集，后验因果作用：

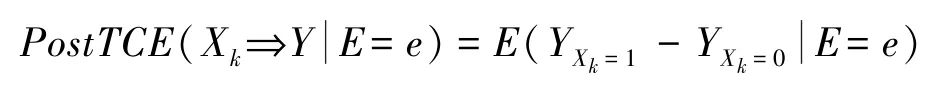
表示根据观测到的证据E ＝e，度量Xk导致结局Y ＝1的因果作用。特别地，p ＝1 时，

后验因果作用的识别假定没有未观测的混杂因素。并假定单调性：

（1）X有单调性：对，有（Xi）Ai ＝a*i≤（Xi）Ai ＝ai（i ＞k）。

（2）Y有单调性：对，有YX ＝x*≤YX ＝x。

在儿童白血病的归因问题中，X有单调性意味着由于家装导致接触油漆涂料的单调性：（X2）X1＝0≤（X2）X1＝1。Y有单调性意味着家装、接触油漆涂料和不爱吃蔬菜水果对白血病没有预防性：YX1＝0，X2＝0，X3＝0≤YX1＝0，X2＝0，X3＝1≤YX1＝0，X2＝1，X3＝1≤YX1＝1，X2＝1，X3＝1，YX1＝0，X2＝0，X3＝0≤YX1＝1，X2＝0，X3＝0≤YX1＝1，X2＝0，X3＝1≤YX1＝1，X2＝1，X3＝1，等。

在单调假定下，可以得到下面等式：

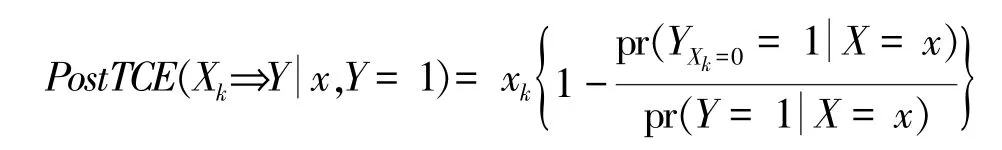
进一步在无混杂假定下，上面潜在结果YXk ＝0的概率可识别

这里ck+1：p ＝（ck+1，…，cp）。

当只观测到原因变量X的子集X＇时，证据（X＇＝x＇，Y ＝1）的后验因果作用等于

有关后验因果作用的其他应用可参见文献［32］。

6 结束语

除了本文已介绍的代理推断、因果网络学习和归因问题，因果推断研究的中介分析（Mediation Analysis）、干涉分析（Interference）、数据融合（Data Fusion）、选择偏差（Selection Bias）和个体化处理（Individualized Treatment Regime）等在社会经济、生物医学研究中都有很重要的应用。限于文章篇幅，未一一述及。总之，因果推断为科学研究中评价因果作用、发现因果关系、挖掘因果机制、反事实归因提供了一套严谨的、可行的理论与方法，因果推断与机器学习等方法相结合将大大提高人工智能的可解释性、可迁移性和稳健性；因果推断与应用学科的前沿发展相结合，将推动各个科学领域对因果机制的深度认识。因果推断从理论走向应用面临着相关领域中许多挑战问题，如何确定混杂因素、如何找对照群体、如何找工具变量、如何利用数据之外的领域知识等。在深化因果推断理论方法研究的同时，需要加强因果推断在现实问题中的应用研究。