2021年全国高中数学联赛一道解三角形试题的多解及推广
2022-11-14叶诚理
中学数学杂志 2022年3期
叶诚理
(福建省福清第一中学 350300)
何 灯
(福建省福清第三中学 350315)
1 试题分析
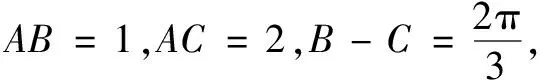
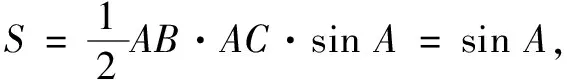
2 试题解析

评注本解法通过正弦定理把边b,c的关系转化成角度B,C的关系,结合三角形内角和关系,运用三角恒等变换公式,转化成与角C相关的三角函数计算问题.

评注本解法仍然是通过正弦定理把边的关系转化成角的关系,与解法1不同之处在于通过联立角A,B,C的关系,把角B,C统一用角A表示,从而得到关于角A的三角关系式,体现了方程思想在解三角形中的应用.


图1
评注本解法通过添加辅助线将角B分解为两个角,从而构造两个相似三角形,再利用余弦定理构建边a的方程,实现了面积的转化计算.
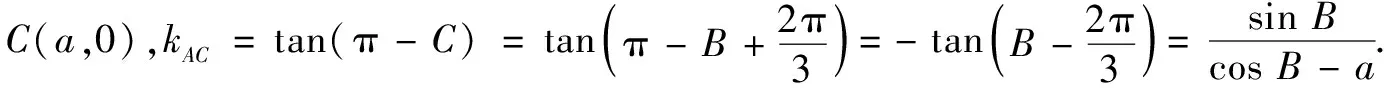

图2
评注本解法通过建立坐标系实现把解三角形问题运用解析几何知识来求解.关键是几何条件代数化,其中,以B为原点的好处是可以根据AB=1把点A看成是单位圆上的点,用角B巧设点A坐标.利用直线AC的斜率表达式,把含边长a的关系式转化成角B的三角函数,进而通过AC距离公式计算sinB,最终转化成面积.
3 试题推广
借鉴解法2,我们可以得到本题在一般情况下的结论.



4 解题心得
条条大道通罗马,本题解法的多样性让我们感受到数学思维的无限魅力.解题中用到的知识涉及函数、方程、三角函数、平面几何、解析几何等;对一般性结论的推广开阔了我们的视野,揭示了问题的本质.本题集中考查了解三角形问题中考生的抽象概括能力、运算求解能力和创新应用意识;用到的数学思想有函数与方程思想(特别是消元思想)、化归与转化思想、数形结合思想等[1].本题的一题多解彰显出灵活合理地运用所学知识解决实际问题的能力的重要性,不仅对竞赛生,也对广大高考生具有一定启发意义,即对数学知识的融会贯通、对数学方法的娴熟运用和对数学思想的深刻领会是考场上制胜的关键[2].
