等离子体性质对磁泡的影响
2022-11-14彭国良张俊杰王仲琦任泽平谢海燕杜太焦
彭国良 张俊杰 王仲琦 任泽平 谢海燕 杜太焦
1)(北京理工大学机电学院,北京 100081)
2)(西北核技术研究所,西安 710024)
利用三维混合模拟程序计算了大量超热碎片离子在低密度背景等离子体中爆炸膨胀的过程.通过定量计算磁泡的变化过程和磁泡对碎片云运动的约束效果,分析了背景等离子体电荷密度、背景离子原子量、碎片离子荷质比等参数对磁泡的影响.计算结果表明,背景电荷密度对磁泡和碎片云的运动有重要影响.在碎片云扩张早期,背景离子原子量对磁泡扩张影响较小,但对后期碎片云的运动有一定影响.当碎片离子荷质比较小时,离子回旋半径大于磁泡半径,此时磁泡半径较小,且磁泡无法约束碎片云.当碎片离子荷质比较大时,离子回旋半径小于磁泡半径,如果此时背景电荷密度较低,磁泡和碎片云的早期扩张几乎不受碎片离子荷质比影响,但对系统后续演化有一定影响,如果此时背景电荷密度较大,碎片离子荷质比对磁泡和碎片云的运动有较大影响.
1 引言
大量超热碎片离子在低密度背景等离子体中爆炸膨胀时,如果存在背景磁场,磁场中会产生磁泡(magnetic bubbles or diamagnetic cavities),即磁场强度极低的区域,此时碎片离子形成的碎片云,在一定条件下能被约束在磁泡内部.这一现象在高空核爆炸[1]、天体物理[2]和激光等离子体实验[3]等领域广泛存在.高空核爆炸产生的磁泡是形成晚期核电磁脉冲的重要机制,磁泡的发展过程对晚期电磁脉冲的强度有重要影响[4],爆炸产生的碎片云含有放射性元素,其运动状态对大气电离、人造辐射带、极光等很多地球物理现象均有重要作用[5].天体物理和激光等离子体实验中,磁泡与等离子体的Rayleigh-Taylor 不稳定性直接相关.因此研究磁泡在工程和学术领域都具有重要意义,也引起了很多学者们的关注[6].当碎片离子运动时,一部分能量传递给磁场,形成磁激波,另一部分传递给背景等离子体,导致背景等离子体运动.Berezin 等[7]的研究表明,碎片能量传递机制取决于阿尔芬马赫数MA(碎片速度与阿尔芬波速度之比).当MA≪1时,能量主要传递给磁场;当MA≫1 时,能量主要传递给背景等离子体.对MA≪1 的情况,Ripin等[8]忽略背景离子的影响,将磁压等效为流体的压力,利用能量守恒得到磁泡最大半径计算公式,该公式没有考虑磁泡实际的三维形状,也没有考虑各种耗散机制.Gisler 等[9]和Winske[10]针对三维形状在Ripin 等[8]的基础上各自给出了修正系数[11,12].修正的公式有助于估算磁泡尺寸的上限,但考虑到实际问题比较复杂,磁泡的发展历程更多依赖实验和模拟得到[13-16].在实际的高空核爆问题中,环境离子密度、碎片离子和环境离子的种类存在很大的不确定性,这种不确定性对磁泡和碎片云分布的定量计算均有一定影响.本文利用三维数值模拟方法研究了背景等离子体电荷密度、背景和碎片离子荷质比等因素对磁泡的影响,并分析了磁泡对碎片云的约束效果.
2 计算模型和方法
2.1 物理模型
以高空核爆炸问题引起的磁泡问题为例,爆炸碎片离子的典型速度约为1.5×106m/s,如用一价铁离子等效碎片离子,地磁场典型值取0.3 G(1 G=10-4T),则对应的运动尺度(回旋半径)约为数十千米量级,相应的电子运动尺度为米量级.流体的适用条件是网格尺度远大于粒子自由程,故对网格尺度千米量级的问题,离子不能用流体描述,可采用PIC(particle-in-cell)模型描述;而电子可作为流体处理,这就是著名的混合模型[17-19].等离子体无碰撞近似满足的条件为[20]
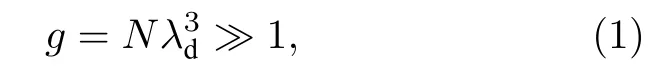
式中,g为等离子体参数,N为电子数密度,λd为德拜长度.
电中性近似需满足的条件为[21]

式中,Δl为网格尺度.无质量电子近似满足条件:

式中,Δt为时间尺度,τe为电子回旋时间,e为电子电荷,me为电子质量,Ve为电子的流体速度,B为磁场.
典型的高空核爆炸碎片云散开到千米尺度时,等离子体密度下降到 1×1012cm-3,则等离子体的德拜长度约为0.005 m,远小于千米级网格尺度,故满足电中性近似;等离子体参数g>1×1011,满足无碰撞近似;关心的时间尺度为0.1 s 级,远大于电子回旋时间尺度0.1 ms 级,故满足无质量电子近似.此时可以得到无碰撞离子的运动方程为
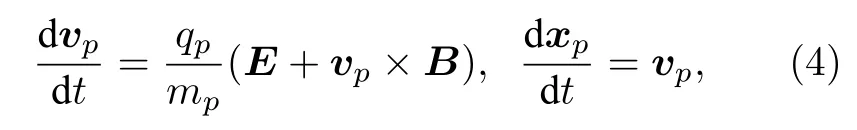
式中,v,q,m,x分别为宏粒子的速度、电荷量、质量和位置坐标;下标p代表第p个宏粒子;E和B为宏粒子感受到的电场和磁场.
若忽略电子的质量,由电子动量方程可得到电场的表达式

式中,ne为电子电荷密度,在电中性近似下等于离子电荷密度;pe为电子压强;η为电阻.在电子温度和密度较小时,可忽略电子压力和电阻,此时电场的表达式进一步简化为

其中,电子的流体速度可以由电流的定义式给出:
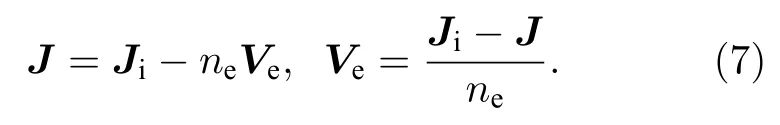
在电子流体速度远小于光速时,满足低频Darwin近似,可忽略麦克斯韦方程的位移电流项,得到简化的电磁场方程:

为便于计算,重新定义电磁场变量以消去磁导率常数µ0:

于是电磁场方程可写为

为保证计算的磁场散度为0,采用广义拉格朗日乘子方法[22],方程(11)修正为

式中,ch和cp为控制参数,建议的取值可参考文献[22].
2.2 计算格式
粒子运动方程采用Boris 时间推进格式[23]计算:

式中,上标n表示当前时间步,n+1 表示下一时间步.(5)式为线性方程组,求解可得到下一时刻宏粒子的位置和速度.记离子的电荷密度为ni和电流密度为Ji,则

式中,W为权函数,可使用CIC(cloud-in-cell)权函数模型给出[24].
求解(11)式的空间积分采用有限体积格式,时间积分利用二阶显式龙格-库塔方法求解,可得到电磁场随时间的演化.
将场方程改写为守恒格式:
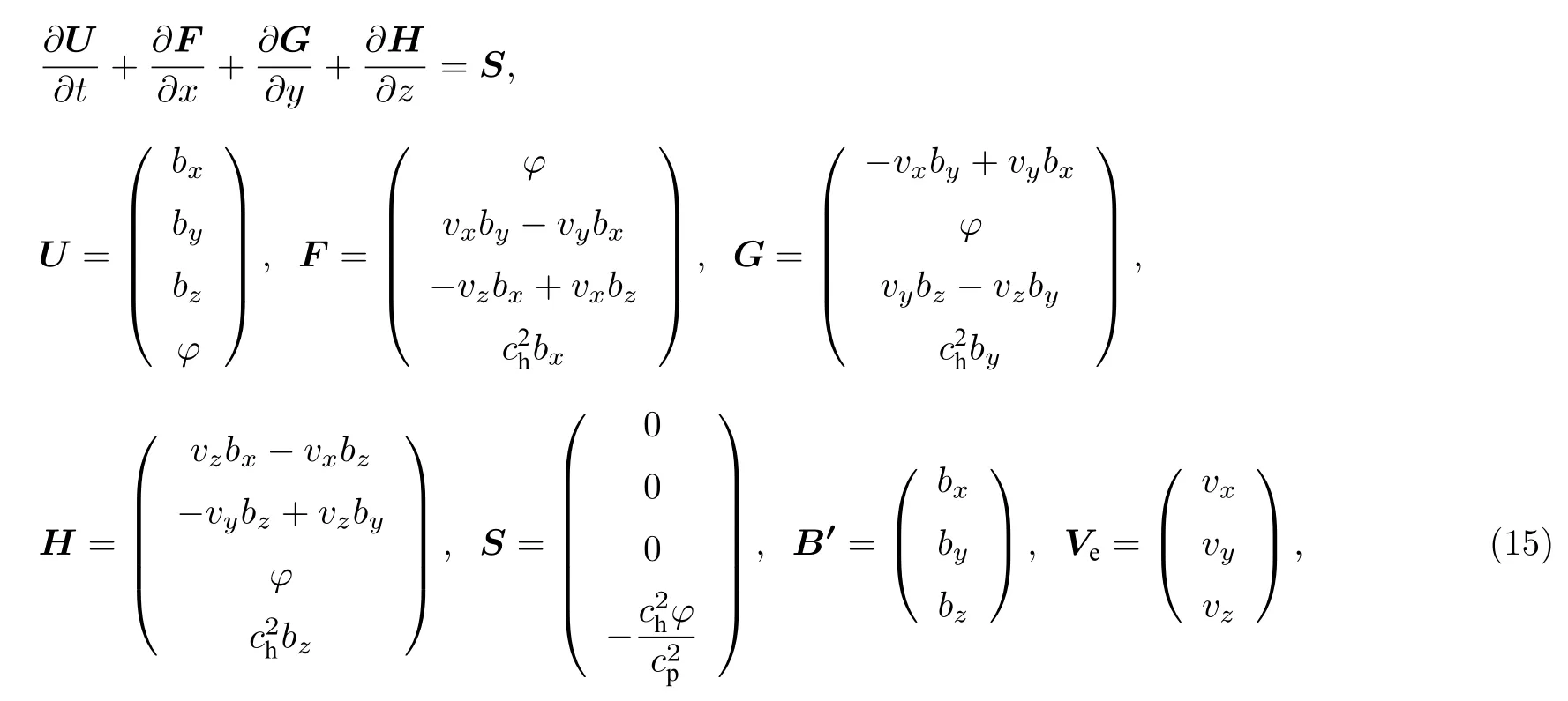
利用有限体积方法可以求解(15)式.含Van-Leer 限制器的二阶守恒重构格式为[25]

通量F,G,H用Lax-Friedrichs 格式计算[26].场变量时间推进格式用龙格-库塔格式:

2.3 程序验证
2.3.1 场方程求解器测试
电荷密度和磁场满足的方程为
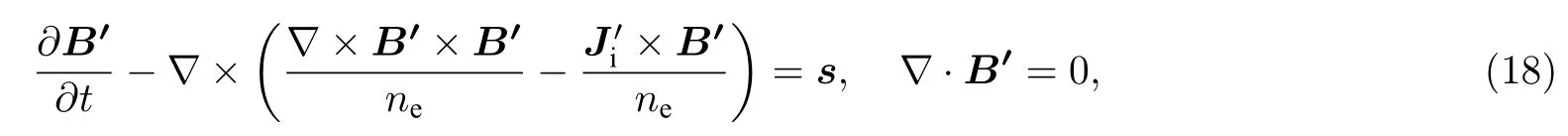
式中,s为磁场方程的配平源项,方程的一组人造解为

通过程序计算得到一组解Bc=,设置误差函数为

计算区域为 [0,1]3,网格数 10×10×10,CFL 数取0.25,计算的误差随时间的变化如图1 所示.从图1 可以看出,计算的磁场误差很小,程序能正确模拟磁场的演化.

图1 磁场误差随时间的变化Fig.1.Variation of magnet field variables error with time.
2.3.2 粒子求解器测试
考虑线性的粒子相对漂移问题.仅考虑时间微分,并假设两种粒子均匀分布,因而所有的空间导数项为0,对应的速度方程可简化为

则问题的解析解为
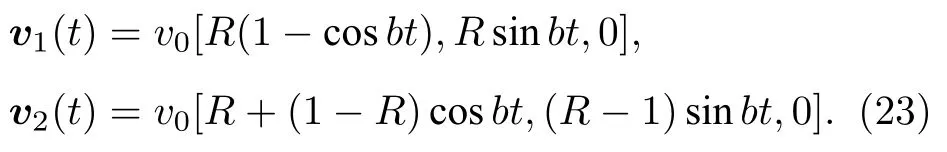
设置误差函数为

式中,上标c 表示程序计算值,exact 代表解析解.
程序计算中取b=2π,v0=5,R=1/2,计算区域为 [0,1]3,计算网格为 10×10×10,两种宏粒子在每个网格上设置1 个,采用周期边界条件,计算得到的误差如图2 所示.由于程序计算中保持严格的动量守恒,两种粒子的误差函数是一样的,因此仅展示了类型1 粒子的误差.可以看出,计算误差很小,程序能正确计算粒子的运动.
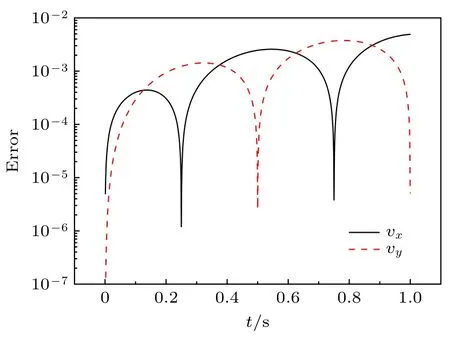
图2 粒子速度误差随时间的变化Fig.2.Variation of particles velocity error with time.
3 分析与讨论
Ripin 等[8]由能量守恒给出:
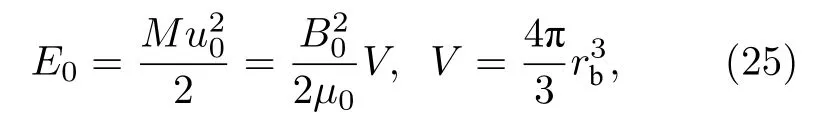
式中,E0为碎片总动能,M为碎片总质量,u0是碎片初速度,B0是背景磁场强度,V为磁泡体积,rb为最大磁泡半径.(25)式给出的最大磁泡半径是全部动能转化为电磁能时磁泡总体积对应的等效半径.实际上在有背景离子存在时,有部分碎片动能转化为背景离子动能,磁泡半径会小于(25)式给出的估计值.由能量守恒得到

式中,ρ为背景离子密度;u为背景离子速度,由于动量守恒的限制,一般不会超过碎片初速度.当背景离子密度很大、背景离子速度等于碎片初速度时,得到文献[13]中提到的等质量半径:
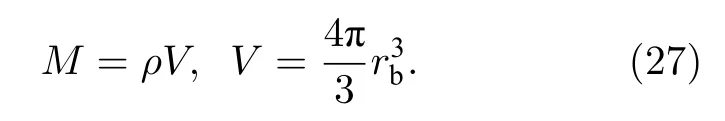
这里M为碎片离子的总质量.实际的背景离子速度尚无解析结果,需要借助数值模拟计算磁泡半径.数值计算得到磁场分布后面临的问题是如何计算磁泡半径.Winske 等[6]指出磁泡是磁场中场强极小的区域(|B|≈0),由于对极小没有明确定义,这个定义公式在实际应用时存在不确定性.为定量分析等离子性质对磁泡和碎片云分布的影响,需对磁泡半径和碎片云分布给出定义.
典型的磁泡云图(即磁场强度大小密度云图)如图3 所示,在图3 中,爆炸发生在中心位置,随着碎片离子向外扩展,逐渐形成磁场强度较低的区域.垂直于磁场的截面一般为圆形,其半径与碎片初始速度垂直于背景磁场方向的分量有关,垂直初速度分量越大,磁泡半径越大;平行于磁场的截面为纺锤形.这里定义磁泡半径Rb为垂直于磁场方向的最大半径:

图3 磁泡云图(a)垂直于背景磁场的截面;(b)平行于背景磁场的截面Fig.3.Magnetic bubbles contour:(a)Cross section perpendicular to background magnet;(b)cross section parallel to background magnet.

式中,B0为背景磁场,S为垂直于背景磁场的平面.碎片云分布的定义可以参照文献[13]的作法,即将包含98%碎片离子的区域定义为碎片离子扩展半径Rd:
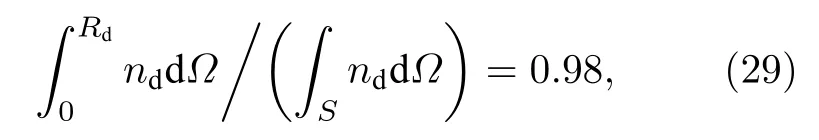
式中,nd为碎片云离子数密度.碎片离子的平均半径Ravg定义为

其中L通常取计算区域的大小.另外为便于比较,定义归一化的磁泡半径δb、碎片云扩散半径δd和碎片云平均半径δavg:
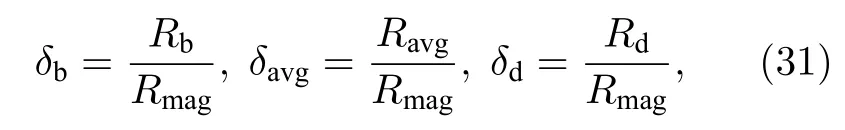
式中,等能量最大磁泡半径Rmag的计算公式为[10]
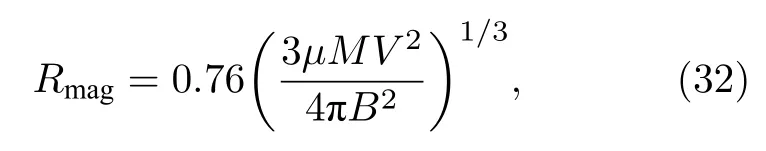
其中,MV2/2 为碎片离子的初始总动能.
计算中设碎片离子和背景离子的电荷数为1,背景离子原子量记为Ab,碎片离子原子量记为Ad,背景电荷密度记为N.设碎片离子总质量M=1 kg,初始均匀分布在半径1 km 的球内,初始速度满足麦克斯韦分布,且平均值vd=1000 km/s,背景磁场B0=0.3 G,则Rmag≈52.7 km,阿尔芬马赫数为
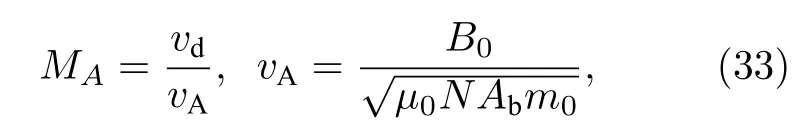
其中,m0为单位原子质量.设计算区域为[-100,100]×[-100,100]×[-60,60].
3.1 背景电荷密度的影响
将背景离子原子量Ab取为16,碎片离子原子量Ad取56,背景电荷密度N分别取1010,1011,1012和1013m-3,对应的阿尔芬马赫数分别为0.61,1.93,6.09 和19.3.其他条件不变,计算背景电荷密度对磁泡半径和碎片云分布的影响.
图4 给出了不同背景电荷数密度下磁泡半径随时间的演化.从图4 可以看出,背景等离子体的电荷数密度越大,最大磁泡半径越小,磁泡的发展越慢.从磁流体角度分析,背景等离子体密度越高,由碎片离子传递给背景离子的能量越多,从而导致磁泡扩张变得困难,磁泡半径变小.另外,背景等离子体密度增大后导致碎片离子平均速度变慢,相应的磁泡发展速度也变慢.从图4 还可以看到: 背景电荷密度较小时,磁泡首先快速扩张到最大值,然后收缩,做周期运动;当背景电荷密度较大时,磁泡扩张到一定大小后,可以较长时间保持相对稳定状态.
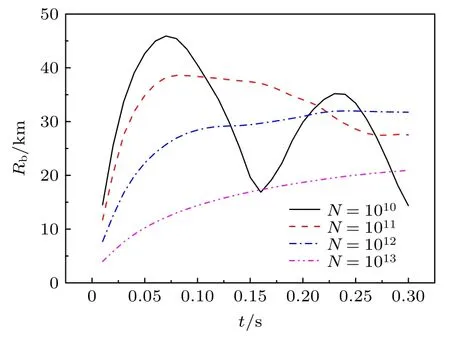
图4 不同背景电荷数密度下磁泡半径随时间的演化Fig.4.Magnetic bubbles radius vs. time under different background charge number density.
图5 给出了不同背景电荷数密度下归一化磁泡半径和碎片云半径随时间的变化.从图5 可以看出碎片云在磁泡中进行周期运动,当背景电荷密度较小时,碎片云的运动周期较大,频率较低.由于低电荷密度下磁泡本身也进行周期运动,碎片云的运动会受磁泡运动的影响,其周期(约0.17 s)也与磁泡运动周期(约0.16 s)相当.电荷密度较大时,磁泡的发展较为稳定,碎片云的运动周期主要受碎片离子的回旋周期的影响.从图5 还可以看到,不同背景电荷数密度下碎片云的最大扩展半径都在1.2Rm左右,变化较小,但平均半径差别较大,这可能暗示碎片云的最大半径主要由不与背景等离子体相互作用的碎片离子在背景磁场中的回旋运动决定.当背景电荷密度较小时,碎片云的平均半径与磁泡半径基本相当,这表明碎片云的分布更多集中在磁泡边缘,随磁泡的运动而运动;背景电荷密度较大时,碎片云的平均半径在磁泡内振荡,这表明碎片云在磁泡边缘和中心来回振荡,这与文献[15]的现象一样.
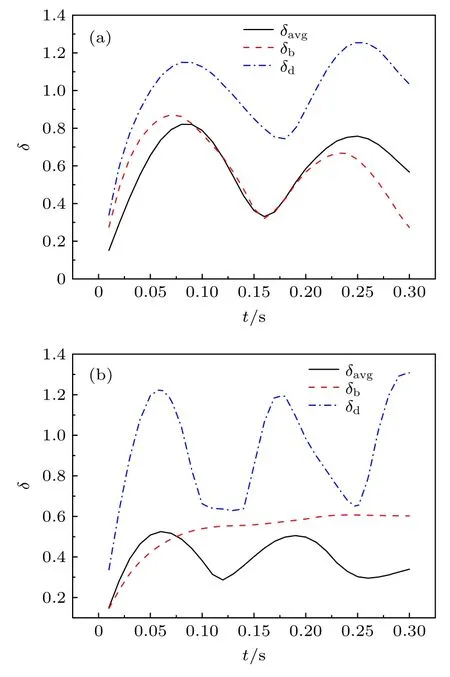
图5 归一化磁泡半径和碎片云半径随时间的变化(a)N=1×1010 m-3;(b)N=1×1012 m-3Fig.5.Normalization debris radius and magnetic bubbles radius vs.time:(a)N=1×1010 m-3;(b)N=1×1012 m-3.
3.2 背景离子原子量的影响
改变背景离子的原子量会影响背景离子的质量密度和阿尔芬波速,还会影响背景离子的回旋半径和周期.取背景电荷密度N分别为1010和1012m-3,背景离子的原子量Ab分别取16,32 和64,碎片离子原子量Ad取56,其他条件不变,计算此时背景离子原子量对磁泡半径和碎片云分布的影响.
图6 所示为不同背景离子原子量下磁泡半径随时间的变化.由图6 可知,背景离子原子量较大时,早期磁泡发展速度变慢,高背景电荷密度下,这种影响更显著.从图6 还可以看到,低背景电荷密度下,背景离子原子量较大时,最大磁泡半径较小,振荡的幅值也较小;高背景电荷密度下,背景离子质量的变化对最大磁泡半径的影响较小.

图6 不同背景离子原子量下磁泡半径随时间的变化(a)N=1×1010 m-3;(b)N=1×1012 m-3Fig.6.Magnetic bubbles radius vs. time with different background ion atomic weight:(a)N=1×1010 m-3;(b)N=1×1012 m-3.
图7 给出了N=1010m-3时不同背景离子原子量下碎片云半径随时间的变化.从图7 可以看到,低背景电荷密度下,背景离子原子量越大,碎片云的平均半径和扩展半径的最大值都会减小.第1 个扩张-收缩周期内不同背景离子原子量对碎片云的分布影响较小,第1 个周期后影响较大.

图7 N=1×1010 m-3 时不同背景离子原子量的碎片云半径随时间的变化(a)Ravg;(b)RdFig.7.Debris radius vs.time at N=1×1010 m-3 under different background ion atomic weight:(a)Ravg;(b)Rd.
图8 所示为N=1012m-3时不同背景离子原子量下碎片云半径随时间的变化.由图8 可知,高背景电荷密度下,背景离子原子量对碎片云第一次扩张的影响很小,对碎片云开始收缩后的影响较大,Ab值越大,第1 个波谷的碎片云半径越小.这表明背景离子的原子量对碎片云半径的影响主要在背景离子密度较低时显现.

图8 N=1×1012 m-3 时碎片离子半径随时间的变化(a)Ravg;(b)RdFig.8.Debris radius vs.time at N=1×1012 m-3 under different background ion atomic weight:(a)Ravg;(b)Rd.
3.3 碎片离子荷质比的影响
固定电荷数,增大碎片离子的原子量相当于减少荷质比.在总质量一定时,改变碎片离子的荷质比会影响碎片离子的总电荷数,还会影响碎片离子的回旋半径和周期.取背景等离子体电荷密度分别为1010和1012m-3,背景离子的原子量Ab为16,碎片离子原子量Ad分别取为14,28,56 和235,对应的回旋半径分别为4.84,9.68,19.4 和81.3 km,其他条件不变,计算背景电荷密度对磁泡半径和碎片云分布的影响.
图9 所示为不同碎片离子原子量下磁泡半径随时间的变化.由图9 可知,无论电荷密度高低,如果碎片离子原子量过大,荷质比过小,则离子回旋半径大于最大磁泡半径,此时最大磁泡半径会显著减小.对离子回旋半径小于最大磁泡半径的情形,当背景离子电荷密度较低时,荷质比对最大磁泡半径影响较小,但对磁泡后续的收缩过程有一定影响,Ad越大,磁泡收缩时波谷半径越小,磁泡的周期也会略微延长;当电荷密度较大时,Ad越大、荷质比越小,最大磁泡半径越大.
图10 和图11 分别给出了低背景电荷密度和高背景电荷密度时不同碎片离子原子量下碎片云半径随时间的变化.可以看出,当碎片离子原子量较大时,碎片云平均半径明显超出磁泡半径,扩展半径很快超出计算域,这表明磁泡约束失效,部分碎片离子已逃逸出计算域.因此只考虑磁泡约束有效的情形.低电荷密度下,碎片离子原子量对碎片云的第1 次扩张的影响很小,但对后续的振荡过程有影响;Ad增大时,振荡周期变长,幅值增大.高电荷密度下,碎片离子质量增大时,碎片云最大平均半径和扩展半径都会增大,振荡周期变短,幅值增大.
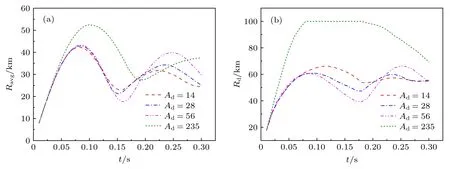
图10 N=1010 m-3 时不同碎片离子原子量下碎片云半径随时间的变化(a)Ravg;(b)RdFig.10.Debris radius vs.time at N=1010 m-3 under different debris ion atomic weight:(a)Ravg;(b)Rd.

图11 N=1×1012 m-3 时不同碎片离子原子量下碎片云半径随时间的变化(a)Ravg;(b)RdFig.11.Debris radius vs.time at N=1×1012 m-3 under different debris ion atomic weight:(a)Ravg;(b)Rd.
图12 所示为归一化碎片云平均半径和磁泡半径随时间的变化.由图12 可知,在低电荷密度下,不同碎片离子原子量的碎片云平均半径与磁泡半径相当,表明碎片云一直集中在磁泡边缘.高电荷密度下,在磁泡稳定期,碎片离子原子量较小的碎片云平均半径远小于磁泡半径,表明碎片云集中在磁泡内部;碎片离子原子量较大的碎片云平均半径的波峰与磁泡半径相当,波谷远小于磁泡半径,表明碎片云在磁泡边缘与内部振荡,这与Winske 等[13]在二维计算得到的结论一致.
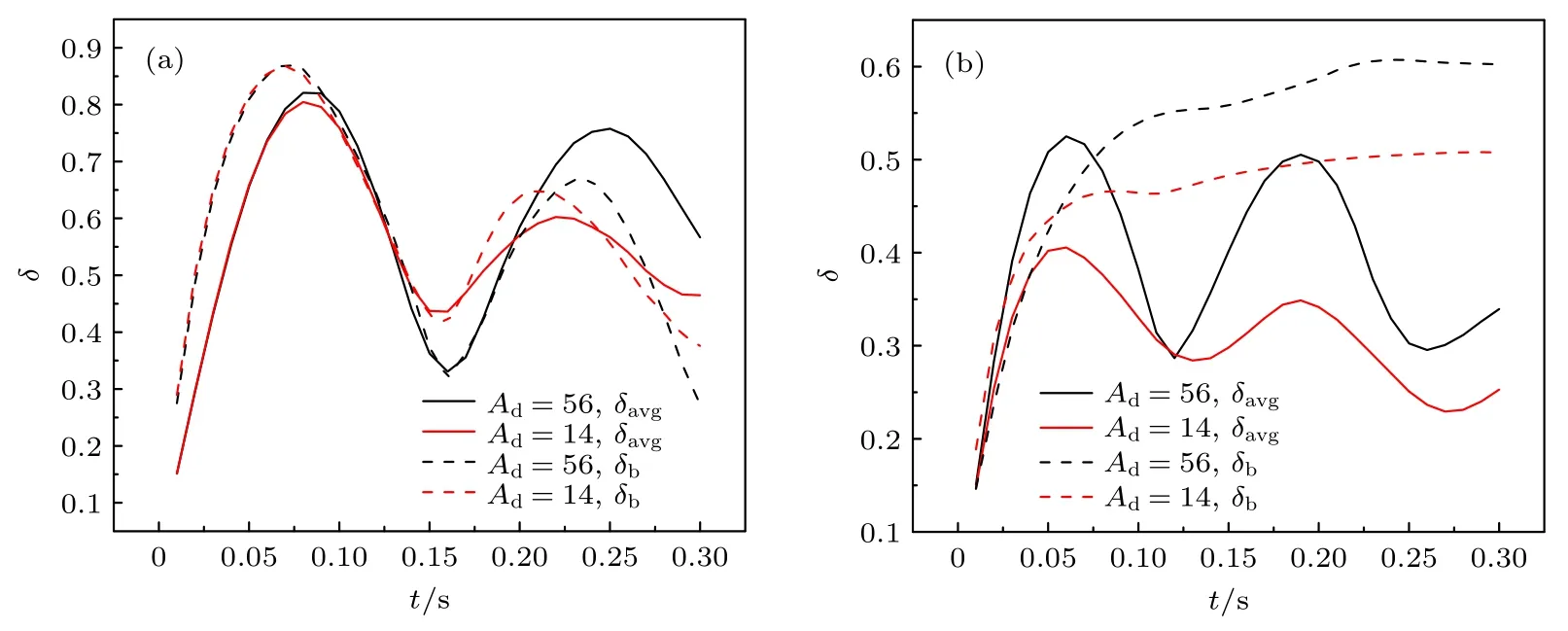
图12 不同碎片离子原子量下归一化碎片云半径和磁泡半径随时间的变化(a)N=1×1010 m-3;(b)N=1×1012 m-3Fig.12.Normalization debris radius and magnetic bubbles radius vs.time under different debris ion atomic weight:(a)N=1×1010 m-3;(b)N=1×1012 m-3.
4 结论
本文用三维混合粒子模拟程序研究了大量超热碎片离子在含背景磁场的低密度背景等离子体中爆炸膨胀过程.通过定义磁泡半径、碎片云扩张半径和平均半径,研究了背景等离子体的电荷密度、背景离子原子量和碎片离子荷质比对磁泡发展过程的影响,并分析了磁泡对碎片云的约束效果.计算结果表明,背景等离子体的电荷数密度越大,最大磁泡半径就越小,磁泡的发展越缓慢;当背景电荷密度较小时,磁泡做周期振荡,碎片云集中在磁泡边缘并跟随磁泡做周期运动.如果背景电荷密度较大,当磁泡扩张到一定大小后,其可以较长时间保持相对稳定状态,此时碎片云在磁泡内部和边缘振荡.如果保持背景等离子体电荷密度一定,当背景离子原子量增大时,磁泡发展速度变慢,该现象在背景电荷密度较高时会更显著.在低背景电荷密度下,当背景离子原子量较大时,最大磁泡半径较小,磁泡振荡的幅值也较小;在高背景电荷密度下,背景离子原子量的变化对最大磁泡半径的影响较小.背景离子原子量对碎片云早期的扩张影响不大,但对后期的碎片云分布有一定影响.当碎片离子荷质比过小时,离子回旋半径大于磁泡半径,此时磁泡半径会显著减小,且磁泡无法约束碎片云.当碎片离子荷质比较大时,如果此时背景离子电荷密度较低,碎片离子荷质比对最大磁泡半径影响较小,但对磁泡后续的收缩过程有一定影响;当背景离子电荷密度较大时,碎片离子荷质比越小,最大磁泡半径越大.低背景等离子体电荷密度下,碎片离子荷质比对碎片云早期扩张的影响很小,但对后续的振荡过程有影响.高背景等离子体电荷密度下,荷质比较大时,碎片云集中在磁泡内部;荷质比较小时,碎片云在磁泡边缘和内部之间振荡,碎片离子荷质比减小后,碎片云最大平均半径和扩展半径都会增大,振荡周期变短,幅值增大.
