SiO2/聚四氟乙烯复合介质材料热性能和介电性能的数值模拟*
2022-11-14刘曰利赵思杰陈文周静
刘曰利 赵思杰 陈文 周静†
1)(武汉理工大学材料科学与工程学院,硅酸盐建筑材料国家重点实验室,武汉 430070)
2)(武汉理工大学材料科学与工程学院,材料复合新技术国家重点实验室,武汉 430070)
SiO2/聚四氟乙烯(polytetrafluoroethylene,PTFE)复合介质材料的热膨胀系数和介电常数主要受到SiO2填充量的影响,如何准确预测其影响至今仍是一个很大的挑战.本文通过数值模拟系统地研究SiO2/PTFE 复合介质材料的热膨胀系数和介电常数.结果表明,随着SiO2 填充量的增加,SiO2/PTFE 复合介质材料的热膨胀系数降低,介电常数增加,且与文献报道数据取得良好的一致性(Han K K,Zhou J,Li Q Z,Shen J,Qi Y Y,Yao X P,Chen W 2020 J.Mater.Sci.Mater.Electron. 31 9196).研究发现,实心SiO2 球(体积分数为30%)/PTFE复合介质材料的热膨胀系数最小,为7.5×10-5 K-1;而空心SiO2 球(体积分数为10%)/PTFE 的介电常数最小,为2.06.由于底部的实心SiO2 球充当支撑作用,底部实心SiO2 球较密集的实心SiO2/PTFE 复合介质材料具有更低的热膨胀系数.SiO2 填料的大长径比会降低SiO2/PTFE 复合介质材料的热膨胀系数.成型工艺对实心SiO2/PTFE 复合介质材料的热膨胀系数几乎没有影响.该工作为通过调控SiO2/PTFE 复合介质材料的微观结构来控制其热膨胀系数和介电常数提供清晰的思路.
1 引言
为了适应5 G 时代的高频应用,高频印制电路板(printed circuit board,PCB)基材需要实现低介电常数以减少信号传播延迟和低介电损耗尽量减少信号损耗.为了避免在应用时温度过高引起形状改变和热失效,高频PCB 基材需要具有优异的热稳定性和低热膨胀系数.因此,低介电常数和低热膨胀系数(coefficient of thermal expansion,CTE)复合介质材料的开发受到广泛关注.
聚合物陶瓷复合材料在微波波段具有优异的介电性能,被广泛用于制造微波基片[1].聚四氟乙烯(polytetrafluoroethylene,PTFE)在很宽的频率范围内具有稳定的介电常数和优异的化学稳定性,但PTFE 的高热膨胀系数(CTE 大约为1.09×10-4K-1)使其在实际应用中无法满足电子设备及相关电子器件的有效散热要求[2].降低PTFE 热膨胀系数的方法之一是在PTFE 基材中填充无机玻璃纤维和陶瓷颗粒等填料[3].过去十年来,通过填充合适的陶瓷填料来调整聚合物的热、机械和介电性能的趋势越来越明显[4-17].SiO2因其合适的介电常数和较小的CTE 而被广泛使用.Chen 等[18]使用5 µm 和25 µm 的SiO2作为填料制备SiO2/PTFE 复合介质材料,当该材料中25 µm 的SiO2填充量为60%(质量分数)时,该复合材料具有最高的模量、最低的CTE 和较低的介电性能.Murali 等[4]比较微米和纳米SiO2对复合材料结构和性能的影响,结果表明含有微米填料的复合材料具有较低的介电常数和介电损耗.同时,有研究报告表明填料尺寸越小,复合材料的CTE 越低[19,20].为了获得更低的介电常数,许多研究人员将空气引入复合材料中.Zhou 等[21]制备一系列聚酰亚胺(PI)/空心SiO2球(hollow silica spheres,HSS)复合薄膜.当薄膜中HSS 填充量为10%(质量分数)时,PI/HSS 薄膜的介电常数为2.09.Jiang 和Yuan[22]研究了SiO2粒径分布对SiO2/PTFE 复合材料性能的影响,当复合材料中SiO2填充量(质量分数)为31%(2 µm)和31%(15 µm)时性能最佳.Ndayishimiye 等[23]通过冷烧结制备SiO2/PTFE 复合材料.结果表明,该复合材料在低频下表现出高介电损耗.综合以上研究可以发现,SiO2/PTFE 复合介质材料的热性能和介电性能主要受到SiO2填料的尺寸、填充量、微观结构和分布等影响.
为了准确研究复合材料热性能的影响因素,研究人员利用数值模拟的方法研究其热过程[24-26].Shi 等[27]利用数值模拟研究碳纳米管增强Al 基纳米复合材料的CTE.研究发现,复合材料的CTE 随碳纳米管直径的增加呈非线性变化,随碳纳米管体积分数的增加呈线性下降.Hassanzadeh-Aghdam和Ansari[28]用微机械方法研究纤维排列对单向纤维增强金属基复合材料(metal matrix composites,MMC)热膨胀行为的影响.结果表明,除体积分数外,纤维的形状和排列对MMC 的横向CTE 也具有显著影响.Chawla 等[29]使用数值模拟研究SiC颗粒体积百分比对Al/SiC 复合材料CTE 的影响规律,结果表明,随着SiC 体积分数的增加,Al/SiC 复合材料的CTE 逐渐降低,Al/SiC 复合材料的CTE是各向异性.Gurrum 等[30]提出球体随机堆积的方法,并结合有限元法计算材料特性: 对于低体积分数含量的填充物,数值模拟结果和分析解决方案非常吻合;对于高体积分数含量的填料,数值模拟结果和分析模型之间存在一些差异,这种差异归因于填充物颗粒在靠近时的多体相互作用效应.复合介质材料中填料的不均匀分布对复合材料的CTE也有重要影响.然而,对影响因素的准确预测仍然是一个巨大的挑战.
本文通过使用COMSOL Multiphysics 软件对SiO2/PTFE 复合介质材料的热性能和介电常数的影响因素进行数值模拟,如实心SiO2球(solid silica spheres,SSS)和 HSS 的填充量、SiO2的显微结构、分布、成型参数等.研究结果有望发展一个新的物理模型,以准确地预测SiO2/PTFE 复合介质材料的CTE 和介电常数.
2 数值模型
2.1 几何模型的建立
本文利用C 语言编程的方法对SiO2/PTFE复合介质材料进行建模,保证SSS 或HSS 在PTFE中随机不干涉分布,SSS 和HSS 的粒径分别为7 µm和1.5 µm[31].SSS/PTFE 复合介质材料的模型尺寸为30 µm×30 µm×30 µm.由于HSS 的粒径小于SSS 的粒径,因此HSS/PTFE 的模型尺寸为10 µm×10 µm×10 µm.在SiO2/PTFE 复合介质材料中,SiO2的填充量(体积分数)分别为10%,15%,20%,25%和30%.SSS 和HSS 填充量为30%的SiO2/PTFE 复合介质材料模型图如图1 所示.为简化计算,假设PTFE 和SiO2的物性参数是各向同性,SiO2球有统一的粒径,SiO2/PTFE 复合介质材料的表面平整光滑等.

图1 SiO2/PTFE 复合介质材料的几何结构(a)SSS;(b)HSSFig.1.Geometric structure of the SiO2/PTFE dielectric composite:(a)SSS;(b)HSS.
2.2 控制方程
热膨胀的计算方程为

其中,α是材料的热膨胀系数,也是温度的函数;εth是热膨胀应变;T是SiO2/PTFE 复合介质材料的温度;Tref是参考温度.随着外界温度升高,空气通过对流机制将热量传递给SiO2/PTFE 复合介质材料.SiO2/PTFE 复合介质材料的温度随着外界温度的升高而升高.SiO2/PTFE 复合介质材料的温度升高对应于其热膨胀和热应力的产生.根据傅里叶公式和能量守恒定律,可得到固体热传导方程:

其中,ρ和c是材料的密度和比热容,u是速度,q是传导热通量,Q是热源,k是导热系数(热导率).SiO2/PTFE 复合介质材料表面的传热过程遵循牛顿冷却定律:

式中,q0是对流热通量,h是对流换热系数,Text是SiO2/PTFE 复合介质材料外界的温度.
线弹性材料的控制方程为Duhamel-Hooks方程:

式中,σ是应力,C是弹性矩阵,ε是总应变,ε0是预应变,εth是热应变,σ0是预应力.总应变ε和弹性矩阵C分别表示为

其中,D是位移矢量,ν是泊松比,E是杨氏模量.电荷守恒的控制方程为
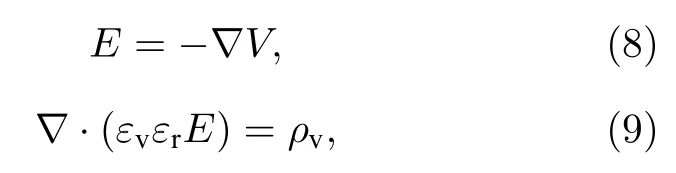
其中,E是电场,V是电势,ρv是空间电荷密度,εr是相对介电常数,εv是真空介电常数.
2.3 材料参数
PTFE 的介电常数很小,而CTE 却很大.为了获得具有较小CTE 和合适介电常数的复合材料,在PTFE 中加入SSS 以降低SiO2/PTFE 复合介质材料的CTE,HSS 会进一步降低SiO2/PTFE 复合介质材料的介电常数.表1 整理了PTFE,SiO2和空气的材料参数.

表1 材料物性参数Table 1.Physical parameters of materials.
2.4 边界条件
SiO2/PTFE 复合介质材料的热通量边界条件如图2 所示,外部温度表示为Text=293.15 +5t[31],垂直壁面上的传热系数(图2(a))表示为

图2 SiO2/PTFE 复合介质材料的热通量边界条件示意图(a)垂直表面;(b)上下表面Fig.2.Schematic diagram of heat flux boundary conditions for SiO2/PTFE dielectric composite:(a)Vertical surface;(b)upper and lower surfaces.

其中,L是SiO2/PTFE 复合介质材料的长度,Ra是瑞利数.
上下表面的传热系数(图2(b))表示为

线性弹性方程组的求解需要相关的固体力学边界条件.在SiO2/PTFE 复合介质材料的上下表面施加10 MPa 的载荷,将固定约束添加到SiO2/PTFE 复合介质材料的下表面,如图3 所示.SiO2/PTFE 复合介质材料的所有其他表面都被认为是自由边界条件,它们会由于热膨胀而自由变形.

图3 SiO2/PTFE 复合介质材料的边界载荷和固定边界条件示意图Fig.3.Schematic diagram of boundary loading and fixed boundary condition for SiO2/PTFE dielectric composite.
介电常数的求解需要相关的静电边界条件.在SiO2/PTFE 复合介质材料的上表面施加1 V电位,并在下表面添加接地边界条件.SiO2/PTFE复合介质材料由390502 个非结构化四面体元素组成,如图4 所示.

图4 SiO2/PTFE 复合介质材料应用非结构化四面体网格Fig.4.Schematic diagram of applied unstructured tetrahedral mesh for SiO2/PTFE dielectric composite.
3 结果和讨论
3.1 SiO2 填充量的影响
通过数值模拟分析SiO2/PTFE 复合介质材料的CTE 和介电常数.SiO2/PTFE 复合介质材料的CTE 由以下关系式计算:

其中,ΔL为热膨胀位移,ΔT为温度变化量,L为材料的原始尺寸.
PTFE 和SiO2的热膨胀位移分布如图5 所示,由于选择SiO2/PTFE 复合介质材料的下表面作为参考面,上表面表现出大的热膨胀位移.通过方程(12)计算得出PTFE 和SiO2的CTE 分别为1.2446×10-4,5.4×10-7K-1.SSS 填充量(体积分数)分别为10%,15%,20%,25%和30%的SSS/PTFE复合介质材料的热膨胀位移分布如图6 所示.由于SiO2对PTFE 的热膨胀具有强的阻碍作用,且SiO2/PTFE 复合介质材料模型中间部分SiO2的体积分数较大,而边缘部分SiO2的体积分数较小.因此,SiO2/PTFE 复合介质材料上表面中间的热膨胀位移小,而边缘位置的热膨胀位移大.SSS/PTFE 复合介质材料的CTE 和介电常数随SSS填充量的变化如图7 所示,当SSS 填充量由10%增加至30%时,SSS/PTFE 复合介质材料的CTE由1.0738×10-4K-1下降至7.5×10-5K-1,其介电常数由2.19 增加至2.48.由于SiO2的CTE 非常小,并且基体的热膨胀受到限制,因此上述结果符合实际情况[18].PTFE 基体的热膨胀由于SiO2随机分布形成物理交联作用而受到阻碍.所以SiO2的填充量越高,PTFE 的热膨胀受到的阻碍则越大,SiO2/PTFE 复合介质材料的CTE 就越小.

图5 Z 轴位移分布示意图(a)PTFE;(b)SiO2Fig.5.Schematic diagram of Z-axis displacement distribution:(a)PTFE;(b)SiO2.

图6 不同SSS 填充量的SSS/PTFE 复合介质材料的位移分布(a)10%;(b)15%;(c)20%;(d)25%;(e)30%Fig.6.Surface displacement distribution map of SSS/PTFE dielectric composite with different filling amounts of SSS:(a)10%;(b)15%;(c)20%;(d)25%;(e)30%.
由图7(a)可以看出,当SSS 填充量小于20%时,SiO2/PTFE 复合介质材料CTE 的计算结果与研究报道[31]的结果非常吻合.当SSS 填充量高于20%时,SiO2/PTFE 复合介质材料CTE 的计算结果与实验结果误差较大,最大偏差为1.8%.这是由于SiO2/PTFE 复合介质材料的几何模型尺寸有限,在内部区域SiO2的体积分数要高于边界处SiO2的体积分数,SiO2之间的距离越近,相互作用越强,因此数值模拟的结果比文献[31]中报道的数据略高.图7(b)显示模拟的介电常数与文献[31]报道的数据基本相同,最大偏差为0.6%,证明当前模型可以准确地预测SSS/PTFE 复合介质材料的CTE 和介电常数.

图7 SSS/PTFE 复合介质材料的CTE 和介电常数随SSS 填充量的变化曲线(a)CTE;(b)介电常数Fig.7.CTE and dielectric constant variations of SSS/PTFE composites with SSS filler contents:(a)CTE;(b)dielectric constant.
为获得低介电常数,将空气限制在SSS 内制备HSS,构建HSS 填充量(体积分数)在10%-30%内的HSS/PTFE 复合介质材料的模型,并计算其CTE 和介电常数.HSS/PTFE 复合介质材料的位移分布如图8 所示.HSS/PTE 复合介质材料的CTE和介电常数的变化曲线如图9 所示,当HSS 填充量由10%增加至30%时,HSS/PTFE 复合介质材料的CTE 由1.1047×10-4K-1降低至8.488×10-5K-1,而介电常数由2.06 增加至2.17.HSS/PTFE 复合介质材料模拟得到的CTE 和介电常数与文献[31]的结果基本一致.CTE 的最大偏差为1.3%,介电常数的最大偏差为0.42%,进一步证实本模型预测HSS/PTFE 复合介质材料的CTE 和介电常数的准确性.

图8 不同HSS 填充量的HSS/PTFE 复合介质材料的位移分布(a)10%;(b)15%;(c)20%;(d)25%;(e)30%Fig.8.Surface displacement distribution map of HSS/PTFE dielectric composite with different HSS filling amounts:(a)10%;(b)15%;(c)20%;(d)25%;(e)30%.

图9 HSS/PTFE 复合介质材料的热膨胀系数和介电常数随HSS 填充量的变化曲线(a)CTE;(b)介电常数Fig.9.CTE and dielectric constant variations of HSS/PTFE dielectric composites with HSS filler contents:(a)CTE;(b)dielectric constant.
通过计算得到HSS/PTFE 复合介质材料中的空气含量.结果表明,对于HSS 填充量(体积分数)分别为10%,15%,20%,25%和30%的HSS/PTFE复合介质材料,其空气体积含量(体积分数)分别为5.12%,7.77%,10.31%,10.67%和12.83%.随着HSS 填充量的增加,HSS/PTFE 复合介质材料中的空气含量增加.由图9 可以看出,HSS/PTFE复合介质材料的CTE 和介电常数随着HSS 填充量的增加呈现非线性变化,这是由于HSS/PTFE复合介质材料中存在空气.其中,HSS 填充量为20%和25%的HSS/PTFE 复合介质材料的介电常数由2.08 增加至2.15,这是由于在HSS/PTFE复合介质材料中SiO2填料的填充量由20%增加至25%时,空气含量只有略微增加,由10.31%增加至10.67%.
比较SSS/PTFE 和HSS/PTFE 复合介质材料,发现相同SiO2填充量的SSS/PTFE 复合介质材料的CTE 较小,这可能是由于SSS/PTFE 复合介质材料的高密度所致.此外,HSS/PTFE 复合介质材料的介电常数较小,可能是由于引入了空气,而空气的介电常数仅为1.由于SSS 的数据与实验结果的匹配程度较高,且SSS 在实际应用中更通用,因此后面的研究工作都采用SSS.
3.2 SiO2 显微结构的影响
SiO2/PTFE 复合介质材料的热性能受界面性质、聚合物和填料的固有性能以及填料形状的影响很大[32].通过构建SiO2填充量(体积分数)为5%的SiO2/PTFE 复合介质材料模型探讨SiO2填料显微结构对其CTE 的影响规律.SiO2显微结构有多种,包括球状、纤维状和薄片状.SiO2纤维和薄片的长径比分别定义为直径与高度之比和高度与宽度之比,而SiO2球的长径比为1.SiO2纤维的长径比分别为5,10,20,其直径为1 µm,长度分别设为5,10,20 µm.SiO2薄片的长径比分别为5,10,20,其长度和宽度均为1 µm,高度分别设为5,10,20 µm.纤维状SiO2/PTFE 复合介质材料和片状SiO2/PTFE复合介质材料的位移分布分别如图10和图11 所示,其CTE 值见图12.由于纤维状和薄片状SiO2在Y轴和Z轴的长度均相同,在X轴的长度大于Y轴和Z轴的长度,因此纤维状和薄片状SiO2/PTFE复合介质材料的CTEy和CTEz表现为各向同性,而CTEx表现为各向异性.球形SiO2在X,Y,Z轴的长度均相等,因此球形SiO2/PTFE 复合介质材料的CTEx,CTEy和CTEz表现为各向同性.SiO2的长径比越大,SiO2/PTFE 复合介质材料在纤维排列方向的性能越好.由于SiO2/PTFE 复合介质材料中纤维状和薄片状SiO2的排列方式平行于X轴,SiO2在X轴方向可有效阻碍PTFE 的热膨胀,因此SiO2/PTFE 复合介质材料的CTEx随SiO2长径比的增加而减小.SiO2长径比对复合介质材料横向CTE(即CTEx)和纵向CTE(即CTEy)的影响是完全相反的[33],CTEy和CTEz表现为各向同性,因此SiO2/PTFE 复合介质材料的CTEy和CTEz随SiO2长径比的增加而增加.

图10 不同长径比的纤维状SiO2/PTFE 复合介质材料的X,Y,Z 轴位移分布(a)-(c)长径比为5;(d)-(f)长径比为10;(g)-(i)长径比为20Fig.10.X,Y,Z axes displacement distribution of SiO2/PTFE dielectric composite with different aspect ratios of SiO2 fiber:(a)-(c)Aspect ratio of 5;(d)-(f)aspect ratio of 10;(g)-(i)aspect ratio of 20.

图11 不同长径比的薄片状SiO2/PTFE 复合介质材料X,Y,Z 轴位移分布(a)-(c)长径比为5;(d)-(f)长径比为10;(g)-(i)长径比为20Fig.11.X,Y,Z axes displacement distribution of SiO2/PTFE dielectric composite with different aspect ratios of SiO2 flake:(a)-(c)Aspect ratio of 5;(d)-(f)aspect ratio of 10;(g)-(i)aspect ratio of 20.
由图12 可知 当纤维状SiO2的长径比由5 增加至20 时,SiO2/PTFE 复合介质材料的CTEy和CTEz由1.2649×10-4K-1增加至1.3756×10-4K-1,CTEx由8.595 ×10-5K-1降低至5.664×10-5K-1.对于SiO2薄片,长径比由5 增加至20 时,SiO2/PTFE复合介质材料的CTEy和CTEz由1.278×10-4K-1增加至1.3414×10-4K-1,CTEx由8.396×10-5K-1降低至6.423×10-5K-1.当长径比为5 时,薄片状SiO2/PTFE 复合介质材料的CTEx值小于纤维状SiO2/PTFE 复合介质材料的CTEx值.随着长径比的增加,薄片状SiO2/PTFE 复合介质材料的CTEx逐渐大于纤维状SiO2/PTFE 复合介质材料的CTEx.基于SiO2填充量(体积分数)为5%制备的SiO2/PTFE 材料的CTE 为1.1644×10-4K-1,而长径比为20 的纤维状和薄片状SiO2/PTFE 复合介质材料的CTEx值较小,分别为5.664×10-5K-1和6.423×10-5K-1,这是由于SiO2纤维和薄片是各向异性的,而SiO2球具有各向同性的特性[33,34].
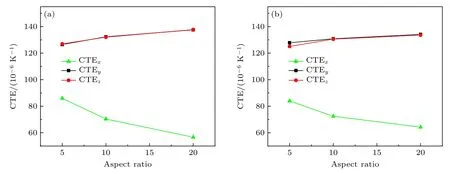
图12 不同SiO2 长径比SiO2/PTFE 复合介质材料的CTE(a)纤维状SiO2;(b)薄片状SiO2Fig.12.CTE of SiO2/PTFE dielectric composite with different aspect ratios of SiO2 filler:(a)SiO2 fiber;(b)SiO2 flake.
3.3 SiO2 分布均匀性的影响
本节通过构建SiO2填充量(体积分数)为15%的SiO2/PTFE 复合介质材料模型探讨SiO2分布均匀性对其CTE 的影响规律.首先,建立PTFE基体模型,将PTFE 模型平均划分为8 份,如图13所示.SiO2球在PTFE 基体中的分布不均匀,其中4 部分为10%,另外4 部分为20%.具有10%和20%SSS 的SiO2/PTFE 复合介质材料的CTE 分别计算为1.0733×10-4K-1和9.047×10-5K-1.
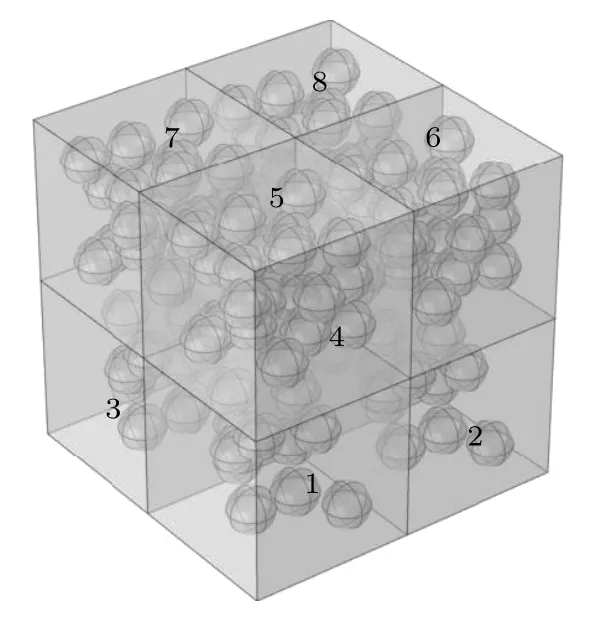
图13 SiO2/PTFE 复合介质材料的SiO2 分布模型Fig.13.SiO2 distribution model of SiO2/PTFE dielectric composite.
SiO2/PTFE 复合介质材料的CTE 列于表2.从表2 可知,当1-4 号分布20%且5-8 号分布10%时,SiO2/PTFE 复合介质材料的CTE 最小,为9.678×10-5K-1;当1-4 号分布10%且5-8 号分布20%时,SiO2/PTFE 复合介质材料的CTE最大,为1.0134×10-4K-1.当将1-4 号中的一个由20%替换为10%时,即将2 号替换为10%,且5-8 号依次替换为20%,SiO2/PTFE 复合介质材料的CTE 基本没有变化,分别为9.785×10-5K-1,9.805×10-5K-1,9.781×10-5K-1,9.780×10-5K-1.这说明SiO2/PTFE 复合介质材料上半部分的随机分布不影响其CTE.当将1-4 号中的两个由20%替换为10%时,则存在两种情况: 一是四条边上的5 号和7 号替换为20%,2 号和4 号替换为10%,其CTE 为9.871×10-5K-1;二是对角线上的6 号和8 号替换为20%且5 号和7 号替换为10%,其CTE 为9.909×10-5K-1.当将1-4 号中的三个由20%替换为10%时,仅存在一种情况: 将上半部分的6-8 号替换为20%,且2 号替换为10%,其CTE为1.0002×10-4K-1.由于底部的SiO2球充当支撑作用,因此底部SiO2球较密集的SiO2/PTFE 复合介质材料具有更低的CTE.
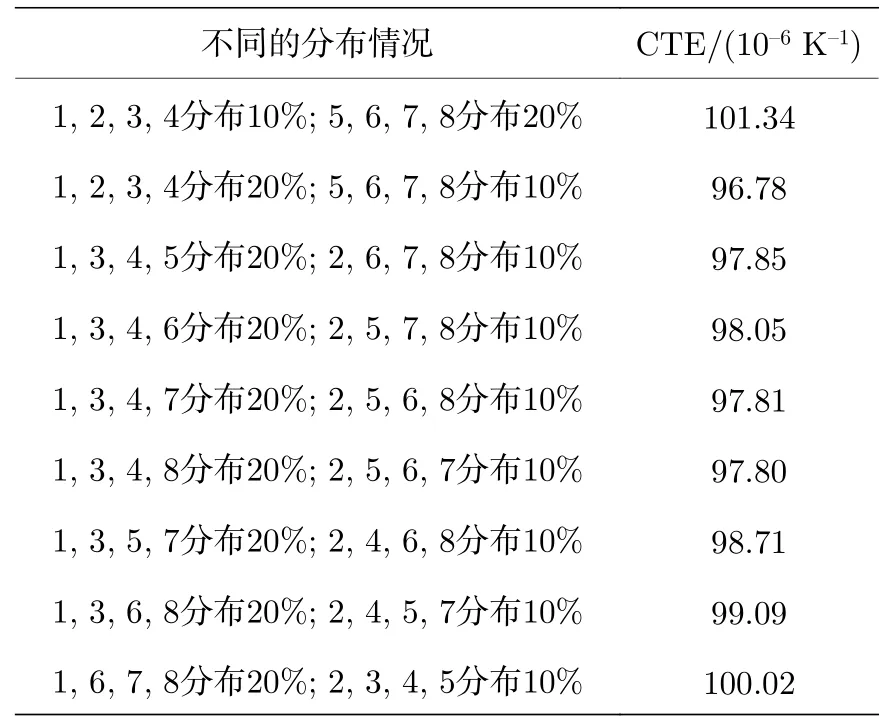
表2 SiO2/PTFE 复合介质材料的CTETable 2.CTE of SiO2/PTFE dielectric composite.
3.4 成型工艺的影响
在SiO2/PTFE 复合介质材料上表面施加5,10,15,20 MPa 载荷,研究成型工艺对其CTE 的影响规律.SiO2/PTFE 复合介质材料上表面热膨胀位移随时间的变化如图14 所示.

图14 SiO2/PTFE 复合介质材料的位移随时间的变化Fig.14.Displacement variations of SiO2/PTFE dielectric composite with different time.
从图14 可以看出,在不同载荷下,SiO2/PTFE复合介质材料的热膨胀位移曲线呈现平行状态.这表明在热膨胀过程中,SiO2/PTFE 复合介质材料上表面的热膨胀位移相同,利用方程(12)计算得出SiO2/PTFE 复合介质材料的CTE 也相同.这是由于不同的成型工艺没有改变SiO2/PTFE 复合介质材料成型的微观结构,因此,SiO2/PTFE 复合介质材料的CTE 也没有变化.
4 结论
采用稳态和瞬态有限元方法对SiO2/PTFE复合介质材料的CTE 和介电常数进行数值研究.详细研究SSS 和HSS 填充量、SiO2的显微结构、均匀性分布和成型参数对SiO2/PTFE 复合介质材料的CTE 和介电常数的影响规律.结果表明,SSS(HSS)/PTFE 复合介质材料的CTE 和介电常数与报道的结果符合良好,30% SSS/PTFE 的CTE最小,为7.5×10-5K-1,而10% HSS/PTFE 的介电常数最小,为2.06.不同微观结构的SiO2对SiO2/PTFE 复合介质材料的CTE 具有明显影响,这归因于片状和纤维状SiO2的各向异性特性.研究发现,由于底部SiO2的支撑作用,底部SiO2分布较密集的复合介质材料具有较低的CTE.此外,成型工艺对SiO2/PTFE 复合介质材料的CTE 几乎没有影响,这是由于SiO2/PTFE 复合介质材料的微观结构在成型过程中没有变化.
