可调自旋-轨道耦合玻色-爱因斯坦凝聚体的隧穿动力学*

马赟娥 乔鑫 高瑞 梁俊成 张爱霞 薛具奎

(西北师范大学物理与电子工程学院,兰州 730070)

研究了在周期驱动拉曼耦合下的可调自旋-轨道耦合玻色-爱因斯坦凝聚体的能带结构、非线性朗道-齐纳隧穿动力学以及隧穿率.利用高频近似得到了与时间无关的Floquet 哈密顿量,发现周期驱动可以有效地调控自旋-轨道耦合和非线性相互作用.与两能级模型对比,解析地得到了能带出现loop 的临界条件以及loop的宽度.研究发现,当种内原子间相互作用等于种间原子间相互作用时,不出现loop 结构.而当种内原子间相互作用小于(大于)种间原子间相互作用时,loop 出现在下(上)能带.此时,自旋-轨道耦合和拉曼耦合都会抑制loop 的出现.特别地,通过调节外部驱动能控制能带出现loop 结构的临界条件.还研究了可调自旋-轨道耦合玻色-爱因斯坦凝聚体的隧穿动力学.通过调节周期驱动强度可以调控系统的隧穿动力学,控制在动量空间发生非线性朗道-齐纳隧穿的位置,并使系统的自旋组分发生翻转.最后计算了系统的朗道-齐纳隧穿率,研究表明周期驱动能够有效调控系统的隧穿率.

1 引言

冷原子中合成人工自旋-轨道耦合的实现使得研究高度可控的玻色-爱因斯坦凝聚体中的许多奇异的量子现象成为可能[1-3].在固态材料中,电子在晶体的本征电场中的运动产生了自旋-轨道耦合,而对中性原子来说可以通过控制光与原子的相互作用来实现,2011 年由NIST 小组[4]首次在实验上设计实现.目前已经展开了很多关于自旋-轨道耦合玻色-爱因斯坦凝聚体的理论研究,如隧穿动力学、基态相图[5-8]、非线性动力学[9-13]、非常规集体偶极振荡[14]、晶格中超流到莫特绝缘体的转变[15]、条纹相内激发谱中的超固体特征[16,17]以及有趣的相对论效应模拟[18,19].对于双组分自旋-轨道耦合玻色-爱因斯坦凝聚体,其能带有两条,呈双阱结构且随着相互作用的增大能带出现loop 结构.这与普通的玻色-爱因斯坦凝聚体完全不同,极大丰富了系统的基态相变[5,7,20,21]和集体动力学[9,22-24].最近的理论研究表明,通过施加弱驱动力加速可以导致系统两个能带之间发生朗道-齐纳隧穿,这在实验和理论上都得到了证实[25-27].

在过去的几年中,周期驱动量子系统引起了越来越多的关注[28].实验上通过周期驱动来实现一个有效Floquet 哈密顿量,使得量子系统的物理可被与时间无关的有效Floquet 哈密顿控制[29,30],从而实现了可调自旋-轨道耦合[31].在自旋-轨道耦合玻色-爱因斯坦凝聚体中,周期驱动也被用于诱导和调控光晶格系统中的自旋-轨道耦合[32],即可以通过快速相干调制拉曼激光强度来调控[33,34].在深光晶格中可调自旋-轨道耦合的玻色-爱因斯坦凝聚体也可产生平带和动力学局域化[29,35].最近发现,自由空间中可调自旋-轨道耦合玻色-爱因斯坦凝聚体的相变可通过外部驱动调节[36].因此,可调自旋-轨道耦合玻色-爱因斯坦凝聚体中有着丰富的能带结构和动力学现象,是一个非常有意义的研究系统.但是,通过拉曼耦合的周期性驱动如何调控系统的能带结构和隧穿动力学仍不清楚,因此本文深入研究了可调自旋-轨道耦合玻色-爱因斯坦凝聚体的能带结构和隧穿动力学.

与两能级模型对比,解析地得到了能带出现loop 的临界条件以及loop 的宽度.研究发现,当种内原子间相互作用等于种间原子间相互作用时,不出现loop 结构,而当种内原子间相互作用小于(大于)种间原子间相互作用时,loop 出现在下(上)能带.此时,自旋-轨道耦合和拉曼耦合都会抑制loop的出现.有趣的是,出现loop 的临界条件和loop宽度随周期驱动强度呈周期性变化.能带不存在loop 结构时,周期驱动强度不改变系统的动力学,即原子沿能带平稳的演化发生了自旋交换.当出现loop 结构时,周期驱动强度的变化使得系统的动力学出现了从非线性朗道-齐纳隧穿到自旋交换动力学的周期性变化,并且使得系统的自旋组分发生了翻转.特别地,周期驱动强度的变化可以精确调控发生非线性朗道-齐纳隧穿动力学的位置.最后计算了系统的隧穿率,研究表明系统的隧穿率可由自旋-轨道耦合、拉曼耦合和周期驱动强度操控.

2 理论模型和能带结构

2.1 理论模型

考虑由Rashba 型和Dresselhaus 型等权叠加的赝自旋为1/2 的自旋-轨道耦合玻色-爱因斯坦凝聚体.在平均场近似下,玻色-爱因斯坦凝聚体可由以下无量纲的Gross-Pitaevskii(G-P)方程描述[29]:

其中,Φ=(Φ1,Φ2)T是两组分凝聚体波函数,而系统单粒子哈密顿量H0=+Vext,其中px是x方向的动量算符,k0是自旋-轨道耦合强度,Ω是拉曼耦合,Vext是外部囚禁势,是泡利矩阵.HI是系统原子间相互作用哈密顿量.无量纲的两体相互作用可以表示为[37]

不失一般性,考虑g11=g22=g.

为了实现可调的自旋-轨道耦合,考虑一个周期性驱动的拉曼耦合,

其中,Ω0是拉曼耦合的常数部分,ΩM是调制振幅,ω是调制频率,该方案可以在实验中通过改变拉曼激光强度实现.调制频率ω的选择比系统中的其他能量尺度要大得多,在这种高频情况下,可以用高频近似来抵消拉曼耦合中随时间变化的调制项,这已被数值模拟及实验结果证实[29,30].为此,引入幺正变换[34]:

其中Ψ=(Ψ1,Ψ2)T是变换后的凝聚体波函数.

因此,根据Floquet 理论[34]变换之后的哈密顿量可以表示为

其中,J0(χ)是第一类零阶贝塞尔函数,χ=ΩM/ω是拉曼耦合的周期性驱动强度.此时两体相互作用的哈密顿量变换为

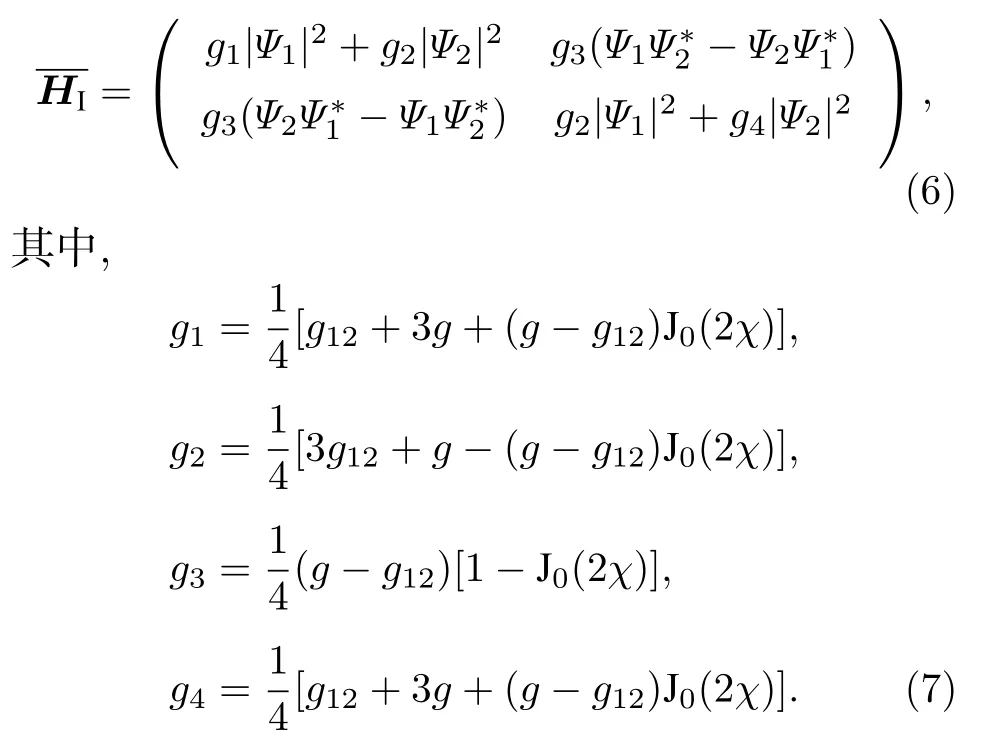
发现经过高频近似后系统在非对角项中出现了新的相互作用项g3,这是由于相互作用不具有SU(2)对称性(即gg12)所导致的.如果相互作用具有SU(2)对称性(即g=g12),则非对角项消失,此时相互作用与周期调制无关.从物理上看,相互作用哈密顿量非对角项出现的原因是gg12时相互作用哈密顿量和自旋算符不对易,相互作用哈密顿量和自旋算符没有共同的本征函数系,所以进行自旋相关的幺正变换以后相互作用哈密顿量就会出现非对角的矩阵元.

假设试探波函数Ψ=,不考虑外部囚禁势(Vext=0),将试探波函数代入G-P方程可得到如下玻色-爱因斯坦凝聚体的动力学方程:

考虑系统的基态,假设φ=e-iµtφ(φ=(φ1,φ2)T),可得到系统的能量方程:

数值求解方程(9)可得到系统在不同相互作用关系下的能带结构.对于双组分的自旋-轨道耦合玻色-爱因斯坦凝聚体,系统能带有两条.从方程(9)可以看出,周期驱动拉曼耦合修正了系统的自旋-轨道耦合项和非线性相互作用项.因此可以通过周期驱动拉曼耦合调控系统的基态能量µ进一步改变系统的基态能带结构.

2.2 能带结构

图1 是在不同系统参数下的能带.显然,系统的能带结构可以由周期驱动强度χ调控.从图1 可以发现,能带在k=0 处出现了loop 结构,且随着相互作用关系的变化,loop 可出现在上能带或下能带.当种内原子间相互作用小于种间原子间相互作用时(g＜g12)loop 出现在下能带,且随着周期驱动强度χ的增加loop 宽度逐渐减小出现尖点,见图1(a1)和图1(a2).而当种内原子间相互作用大于种间原子间相互作用时(g＞g12),loop 出现在上能带,此时增加周期驱动强度χ也使得能带的loop宽度减小并且出现尖点,直至能带光滑,见图1(c1)和图1(c2).特别地,当两者相等时(g=g12),不出现loop 结构.此时虽然增大了周期驱动强度χ,但是能带中仍然不出现loop 结构,仅改变了能带的形状,见图1(b1)和图1(b2).如图1 的第一列和第三列所示,自旋-轨道耦合和拉曼耦合增大可以有效减小loop 的宽度.因此系统loop 结构的存在由自旋-轨道耦合、拉曼耦合和周期驱动强度的耦合效应所决定,实验中可以通过改变周期驱动的驱动强度有效操控loop 的出现.

为了详细研究图1 中所展示的各参数对能带结构的影响,下面将其映射到非线性两能级模型中,研究能带出现loop 结构的临界条件.通过使用归一化条件|φ1|2+|φ2|2=1,可以将方程(9)写成µntlφ=Hntlφ,其中

图1 动量空间中不同相互作用关系下的能带结构(a1),(a2)g=0.0＜g12=0.7;(b1),(b2)g=g12=0.7;(c1),(c2)g=1.5＞g12=0.7Fig.1.Energy band structure in momentum space under different interactions:(a1),(a2)g=0.0＜g12=0.7;(b1),(b2)g=g12=0.7;(c1),(c2)g=1.5＞g12=0.7.

则非线性两能级哈密顿量可写为如下形式:

其中σi是泡利矩阵.(10)式中第一项是等效自旋-轨道耦合能,第二项是等效非线性相互作用能,第三项是拉曼耦合能.拉曼耦合使上下能带发生耦合,并使能带免交叉,且在k=0 处产生间距为Ω0的带隙.而能带在k=0 处出现loop 结构主要是拉曼耦合能和等效相互作用能之间竞争的结果.只有当等效非线性相互作用能占优,即等效非线性相互作用能大于拉曼耦合能时能带才会出现loop 结构.当种内原子间相互作用与种间原子间相互作用相等时(g12=g),等效相互作用能为0,此时能带无法出现loop 结构.则可以得到出现loop 结构的临界条件为=Ω0.loop 结构出现在上能带还是下能带是由等效非线性相互作用是吸引还是排斥决定的.当种间原子相互作用占优时(即g＜g12),＞0,等效非线性相互作用能为排斥的,loop 结构出现在下能带,而当种内原子间相互作用占优时(即g＞g12),＜0,等效非线性相互作用能为吸引的,loop 出现在上能带.为了更为直接地展示不同参数对出现loop 结构的影响,在图2 中给出了不同种内原子间相互作用下,出现loop 结构的临界拉曼耦合Ω0的变化图.可以看出,g-Ω0平面对于固定的种内原子间相互作用g,存在一个临界拉曼耦合Ωc,只有Ω0＜Ωc能带才能出现loop 结构,而且临界拉曼耦合随着周期驱动强度χ的增大先减小后增大.当g＜g12时,等效非线性相互作用是排斥的,下能带出现loop 结构.而g＞g12时,等效非线性相互作用是吸引的,上能带出现loop 结构,并且Ωc随着|g12-g|的增大而增大.

图2 不同周期驱动强度下能带出现loop 结构的临界拉曼耦合 Ω0 随种内原子间相互作用的变化规律.g12=0.7.图中“Loop down”表示loop 出现在下能带,“Loop up”表示loop 出现在上能带Fig.2.Critical Raman coupling Ω0 as a function of intraspecies atomic interaction for different periodic driving strength with g12=0.7 .“Loop down” means that the loop appears in lower band,while “Loop up” means that the loop appears in upper band.

从图2 可以看出,周期驱动强度对能带出现loop 结构有着非常显著的影响.为了更直观地展示周期驱动强度对于出现loop 结构的临界条件的影响,图3(a)和图3(b)分别给出了g＜g12和g＞g12情况下随周期驱动强度χ变化的出现loop 结构的临界拉曼耦合图.可以看出,与图2 类似,在χ-Ω0平面内对于一个确定的驱动强度χ,存在一个临界拉曼耦合Ωc,且Ωc随着种内原子间相互作用g的变化而变化.当种内原子间相互作用g一定时,临界拉曼耦合Ωc的值随着周期驱动强度χ的增大先减小后增大之后又减小,呈周期性变化.总的来说,能带中出现loop 的临界拉曼耦合Ωc随着周期驱动χ的变化呈贝塞尔函数型变化.周期驱动通过调控自旋-轨道耦合能和等效非线性相互作用能的大小,进而改变能带出现loop 的临界条件和loop 结构的大小.但改变周期驱动强度并不能改变等效非线性相互作用能的符号,因此仅改变loop 结构的大小.

图3 不同种内原子间相互作用下出现loop 的临界拉曼耦合 Ω0 随周期驱动强度 χ 的变化规律(a)g＜g12;(b)g＞g12.g12=0.7.图中“Loop down”表示loop 出现在下能带,“Loop up”表示loop 出现在上能带Fig.3.Critical Raman coupling Ω0 as a function of periodic driving strength for different intraspecies atomic interaction:(a)g＜g12;(b)g＞g12 .The other parameters are g12=0.7.“Loop down” means that the loop appears in lower band,while“Loop up” means that the loop appears in upper band.

能带中出现loop 后,其在动量空间存在的区域为-kc≤k≤kc,其中

因此loop 的宽度为 2kc.图4 详细展示了自旋-轨道耦合强度k0、拉曼耦合Ω0和周期驱动强度χ在g＜g12(图4(a1)和图4(a2))和g＞g12(图4(b1)和图4(b2))的情况下对loop 宽度的耦合效应.当g＜g12且Ω0一定时,loop 宽度随着周期驱动强度χ的增加先减小至0 后又增加,继续增大χ,loop宽度又减小(图4(a1)).同样可以发现,g＞g12且Ω0一定时,周期驱动强度对loop 宽度的影响与g＜g12时相同(图4(a2)).从图4 也可以看出,当周期驱动强度χ一定时,在不同相互作用关系下,随着自旋-轨道耦合强度k0和拉曼耦合Ω0的增大,loop 的宽度都减小,也就是抑制了loop 结构的出现.总的来说,发现自旋-轨道耦合强度k0、拉曼耦合Ω0和周期驱动强度χ对loop 宽度存在耦合效应.尤其是周期驱动强度χ的变化使得能带中loop 宽度的变化呈现复杂的周期性,这是可调自旋-轨道耦合玻色-爱因斯坦凝聚体中特有的现象.

图4 (a1),(a2)g＜g12(g=0.2＜g12=0.7)时不同自旋-轨道耦合强度 k0 下loop 宽度随 χ 的变化规律(Ω0=0.3);(b1),(b2)g＞g12(g=1.5＞g12=0.7)时不同拉曼耦合 Ω0 下loop 宽度随 χ 的变化规律(k0=1)Fig.4.(a1),(a2)Loop width as a function of χ for various spin-orbit coupled strength k0 when g＜g12(g=0.2＜g12=0.7)with Ω0=0.3;(b1),(b2)loop width as a function of χ for various Raman coupling Ω0 when g＞g12(g=1.5＞g12=0.7)with k0=1.

3 隧穿动力学

由于原子间非线性相互作用存在,使得能带出现loop 结构.从第2 节可以发现,周期驱动可以有效地调控系统的能带结构.而loop 结构的出现使得系统的动力学受到了显著的影响,即系统的布洛赫振荡被破坏,发生了非线性朗道-齐纳隧穿.因此,可以通过loop 结构的周期变化来研究周期驱动强度对系统隧穿动力学的调控.通过向系统施加非常弱的加速力[25-27],驱动系统的准动量定向移动.假设系统初始状态处于下或上能带(图5(a1)),通过弱加速力缓慢地改变系统的准动量k,使原子发生定向移动.当原子沿上能带运动到loop 边缘时,由于能带的突然中断,原子只能向上或向下跳,即发生了非线性的朗道-齐纳隧穿.因此,本节研究不同周期驱动强度χ下能带的结构和对应的系统动力学.通过对方程(8)进行数值计算模拟系统的隧穿动力学.在动量空间中,加速力F改变准动量,k=kini+αt,其中kini是初始准动量,α是加速度.

图5(a1)-(e1)表示不同周期驱动强度χ下的系统能带.图5(a2)-(e2)和图5(a3)-(e3)分别表示粒子数|φ1|2(图中红色细线)和|φ2|2(图中蓝色细线)在不同初始状态下随时间的演化.玻色-爱因斯坦凝聚体最初制备在系统的下(上)能带由圆(正方形)标记,原子沿箭头所示的方向移动(图5(a1)-(e1)).从图5 可以看出,粒子处于不同的初始状态所对应的动力学是完全不相同的.当周期驱动强度χ=0 且loop 出现在上能带时(图5(a1)),如果粒子初始位于上能带,粒子数初始沿着能带平稳演化,运动到一定的位置,即loop 的边缘时(见图中垂直蓝线),粒子数发生剧烈的振荡(图5(a2)),这证明系统发生了非线性朗道-齐纳隧穿.这可以用于测量loop 的宽度.图5(a2)中两条垂直蓝线的距离正好对应于能带结构中k=0 到loop 边缘的距离.随着周期驱动强度χ的增加,loop 的宽度开始减小,系统发生非线性朗道-齐纳隧穿的位置发生改变,即图中粒子数发生剧烈振荡的位置发生变化(图5(b2)中垂直蓝线).周期驱动强度χ的进一步增加使得能带中不出现loop 结构,此时原子沿上能带平稳地演化,发生了自旋交换(图5(c1)和图5(c2)).继续增加周期驱动强度χ,图5(d1)和图5(e1)中的上能带又出现loop 结构,原子沿上能带运动时又发生非线性朗道-齐纳隧穿,并且发生振荡的位置也发生了改变.下能带中不存在loop结构,原子沿着能带平稳地演化,在一定的时间变得自旋无极化(见图中垂直蓝线),且随着时间的变化,粒子数发生了自旋交换,结果如图5(a3)-(e3)所示.此时虽然改变了周期驱动强度χ,但是发生自旋交换的位置并不发生改变,仍然位于k=0 处.而且,周期驱动强度χ的增加使得自旋组分发生了翻转.当原子初始位于上能带,χ=0时|φ1|2的粒子数接近于1,而随着χ的增大自旋组分发生了翻转,粒子数|φ2|2接近于1(见图5(a2)和图5(e2)).由此可以看出,由于周期驱动强度对loop 结构的调控,使得初始态位于上能带的系统动力学发生了从非线性朗道-齐纳隧穿到自旋交换再到非线性朗道-齐纳隧穿的交替变化.总的来说,周期驱动强度χ的变化不改变自旋交换的位置,但可以精确调控发生非线性朗道-齐纳隧穿的位置.此外,由于两个能带之间的能量差随着准动量而变化,所以振荡周期也发生变化.

图5 (a1)-(e1)存在loop 结构时的能带结构,原子最初制备在系统的上(下)能带用正方形(圆)标记;(a2)-(e2)原子初始制备在上能带中时对应的非线性朗道-齐纳隧穿动力学;(a3)-(e3)原子初始制备在下能带中时对应的非线性朗道-齐纳隧穿动力学.第一行至第四行分别取 χ=0,1,2,3,4. k0=1 ,Ω0=0.3 ,g=1.5 ,g12=0.7,α=0.0001Fig.5.(a1)-(e1)Energy band structure.The Bose-Einstein condensates are initially prepared in the lower(upper)band of the system labeled by the square(circle).(a2)-(e2)The corresponding nonlinear Landau-Zener tunneling dynamics when the atomics are initially prepared in the upper band.(a3)-(e3)The corresponding nonlinear Landau-Zener tunneling dynamics when the atomics are initially prepared in the lower band.From the first row to the fourth row: χ=0,1,2,3,4,respectively.The other parameters are k0=1,Ω0=0.3,g=1.5,g12=0.7,α=0.0001.

4 隧穿率

朗道-齐纳隧穿是量子动力学中的一个基本现象,它描述了在不同的物理系统中靠近免交叉位置处可能发生的非绝热跃迁.而隧穿率与非线性能带结构的变化密切相关,本节通过理论和数值模拟两方面研究可调自旋-轨道耦合系统能带间隧穿率的变化情况.

当g12=g时,也就是不存在等效非线性时,可以用朗道-齐纳模型来描述控制系统量子态在两个绝热本征能级之间的跃迁[25]:

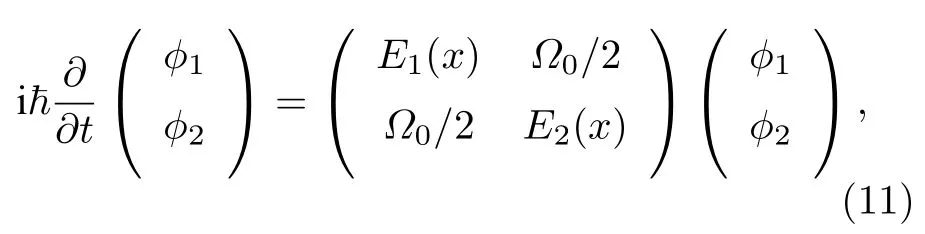
式中,E1,2是φ1,2所对应的能量,Ω0是两个能级之间的耦合参数.此时,隧穿率可以定义为PLZ=exp[-2π(Ω0/2)2/(ħαβ)]. 其中,α是加速度,β=|∂E1/∂x-是能带在xc处的斜率差.根据方程(10)将E1,2代入可得β=2k0J0(χ),因此可以计算得出隧穿率为

其中,k0是自旋-轨道耦合强度,χ是周期驱动强度.当系统处于强相互作用时,可以用稳相近似[40]法推导隧穿率的解析表达式为

其中p=2π(Ω0/2)2/(2αk0J0(χ)).

还可以数值求解系统的隧穿率.假设凝聚体的初始状态为φ=(φ1,φ2)T,经过概率为PNLZ隧穿之后,凝聚体的状态可表示为[33]

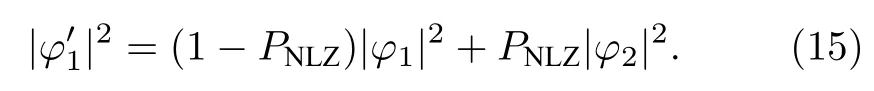
而凝聚体隧穿前后的状态可通过数值模拟方程(8)求得,从而可以数值求出系统的隧穿率,并与理论结果相比较.

图6 不同周期驱动强度 χ 下朗道-齐纳隧穿率随(a)自旋-轨道耦合强度 k0 和(b)拉曼耦合 Ω0 的变化规律(a)Ω0=0.03;(b)k0=1.0.不同形状的符号代表方程(12)给出的理论值,不同的线条代表从方程(8)得到的数值解. g=g12=0.02,α=0.001Fig.6.The Landau-Zener tunneling probabilities as a function of(a)the spin-orbit coupling strength k0 and(b)Raman coupling Ω0 for various periodic driving strength χ:(a)Ω0=0.03;(b)k0=1.0 .The different symbols represent the theoretical values given by Eq.(12)and different lines represent the results obtained by Eq.(8).The other parameters are g=g12=0.02,α=0.001 .

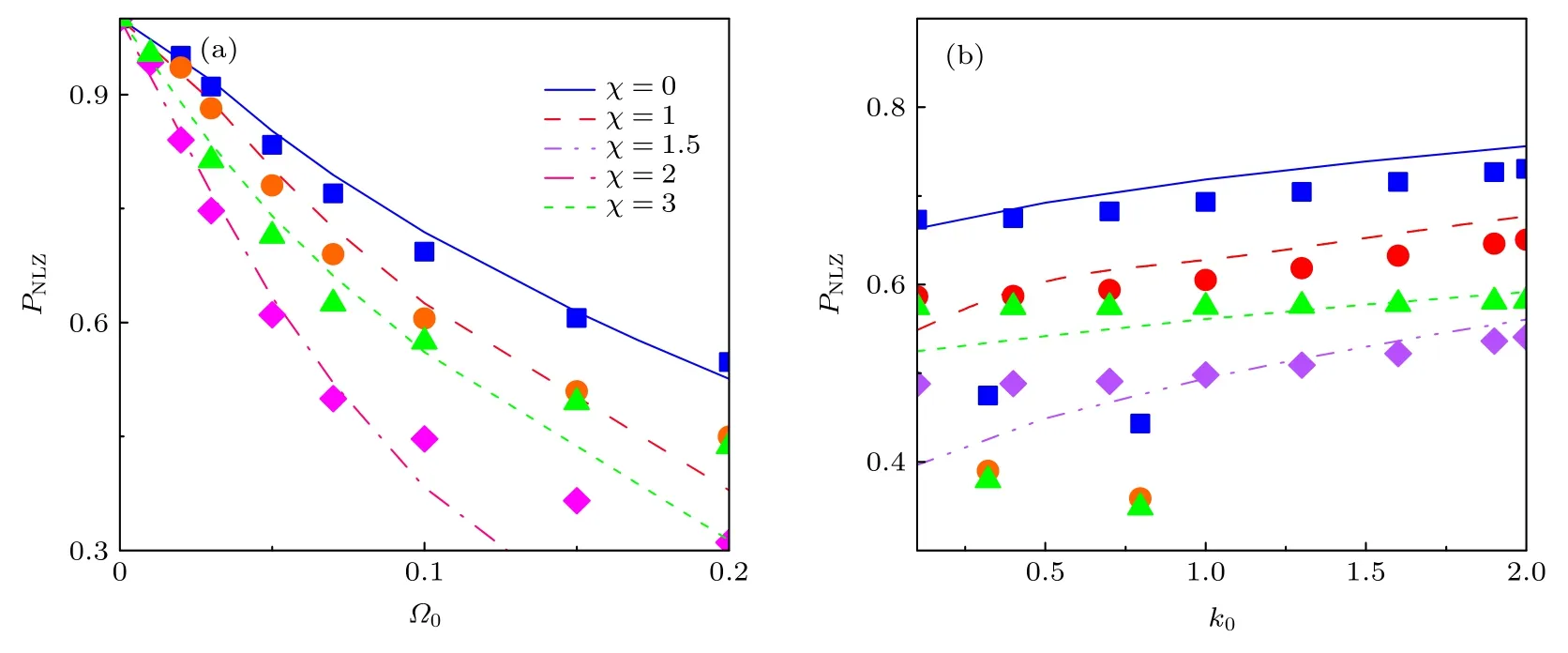
图7 不同周期驱动强度下非线性朗道-齐纳隧穿率随(a)拉曼耦合 Ω0 和(b)自旋-轨道耦合强度 k0 的变化规律(a)k0=1 ;(b)Ω0=0.1.不同形状的符号代表方程(14)给出的理论值,不同的线条代表从方程(8)得到的数值解. g=1.5＞g12=0.7,α=0.005Fig.7.The nonlinear Landau-Zener tunneling probabilities as a function of(a)Raman coupling Ω0 and(b)the spin-orbit coupling strength k0 for various periodic driving strength χ .(a)k0=1 ,(b)Ω0=0.1 .The different symbols represent the theoretical values given by Eq.(14)and different lines represent the results obtained by Eq.(8). The other parameters are g=1.5＞g12=0.7,α=0.005.

5 结论

综上所述,本文研究了可调自旋-轨道耦合玻色-爱因斯坦凝聚体的能带结构、隧穿动力学和隧穿率.通过周期驱动的拉曼耦合,利用高频近似得到了与时间无关的Floquet 哈密顿量.与非线性两能级模型对比,解析地得到了出现loop 的临界条件和loop 宽度.结果表明,能带中出现loop 结构的临界条件可通过改变周期性驱动强度来控制.当种内原子相互作用小于(大于)种间原子相互作用时,loop 结构出现在下能带(上能带).而当两者相等时,不出现loop 结构,能带呈双阱结构.由于loop 结构的存在,系统发生了非线性朗道-齐纳隧穿.而周期驱动强度的这种调控作用可以操控系统的隧穿动力学,并且使系统的自旋组分发生了翻转.最后计算了系统的隧穿率.