光电倍增管输出电子流脉冲堆叠对光子计数法测距的影响
2022-11-14向雨琰李松马跃
向雨琰 李松 马跃
(武汉大学电子信息学院,武汉 430072)
光电倍增管(photomultiplier tubes,PMT)具有光子级别的灵敏度、低暗计数、低后脉冲概率,被广泛应用于可见光波段的光子计数雷达中.PMT 没有光子探测死区时间,每响应一个光子就会输出一个电子流脉冲,这些电子流脉冲有可能堆成规模更大的脉冲,使用阈值鉴别法鉴别光子事件时,堆叠的脉冲会引入额外的脉冲行走误差.考虑到脉冲堆叠的影响,建立了新的PMT 光子探测理论模型,并通过蒙特卡罗仿真,得到了基于PMT 的光子计数测距法的行走误差、测距精度和回波激光脉宽,PMT 输出电子流脉宽以及光子事件鉴别阈值之间的关系.搭建了基于PMT 的激光雷达系统,通过与GM-APD 的对比实验证明了脉冲堆叠对PMT光子计数法测距存在不可忽略的影响.考虑到脉冲堆叠的PMT 光子探测模型能够指导基于PMT 的光子计数雷达的设计,提高测距系统的测距精度和准度.
1 引言
光子计数激光雷达使用具有光子灵敏度的探测器件作为光敏传感器,相对于线性体制激光雷达,光子计数系统需要的回波信号强度可以低2-3 个量级,是远程激光雷达的重要发展方向[1-4].目前常用的单光子探测器有盖革模式的雪崩二极管(GM-APD),硅光电倍增管和光电倍增管(photomultiplier tubes,PMT)[5-7].其中光电倍增管通过多级倍增能够将单个入射光子转换为宏观的电子流输出,其增益可达106-107[8],而且由于PMT 具有暗电流小、后脉冲概率低等优势[9],在可见光波段量子效率高,已经被广泛运用于各种可见光波段的单光子体制的光子计数激光雷达中[10-12].
不同于传统的需要淬灭的单光子探测器件,PMT 在完成一次光子事件的响应之后不需要进行淬灭,依旧能够保持光子探测的能力,所以PMT没有物理意义上的死区时间,PMT 每探测到一个光子都会输出一个宏观电子流脉冲信号[13].但是PMT 的光电子倍增过程存在一定的随机性,电子流中的每个电子从PMT 出射的时间并不相同,所以PMT 输出的电子流脉冲有一定的持续时间,PMT 对到达时间间隔小于电子流脉冲持续时间的多个光子事件响应时,会出现电子流脉冲的堆叠,在窄脉冲激光测距应用中,这种现象非常普遍[14].由于PMT 输出信号的峰值小、脉宽窄,因此一般采用阈值判别法直接对PMT 的输出信号进行时间鉴别.电子流脉冲的堆叠会改变PMT 输出脉冲的幅值,而阈值鉴别法非常容易受到脉冲幅值变化的影响[15],进而影响PMT 输出光子事件时间的准确性.
Donovan 等[16]提出了一个理论模型描述了光子事件堆叠对PMT 光子计数率的影响,并研究分析了光子计数率与鉴别阈值、信号光子数之间的关系,但是他们采用归一化方波近似描述PMT 输出的电子流脉冲,忽略了脉冲上升沿变化对阈值鉴别时刻的影响;Chen 等[17]提出了一个PMT 行走误差的修正模型,但是该模型只考虑了两个光子在同一个事件区间到达时脉冲幅值变化对阈值鉴别的影响,忽略了光子到达时间分布的随机性;Zhang等[18]提出了全新的理论模型和经验公式描述了PMT 脉冲堆叠带来的死区效应,并研究了其对光子计数法激光测距的影响,但此模型也忽略了脉冲幅值变化对光子事件鉴别时刻的影响.目前大部分基于PMT 的光子计数雷达都在使用传统单光子探测理论模型描述PMT 的光子探测概率,并未考虑到脉冲堆叠对光子事件鉴别的影响,导致理论结果和实际结果会存在一定偏差.为提高PMT 光子计数法测距的精度,需研究PMT 电子流脉冲堆叠和光子事件鉴别时间之间的关系.
本文分析了PMT 产生电子流脉冲堆叠的过程,提出了一个新的模型来描述脉冲堆叠对PMT光子事件探测概率的影响,用蒙特卡罗仿真研究了脉冲堆叠对光子计数法测距的测距行走误差和测距精度的影响,并通过实验进行验证.基于该模型,可以在PMT 光子计数雷达的设计阶段对系统参数进行优化,最大限度减小脉冲堆叠带来的测距误差,提升系统的测距精度和准确度.
2 PMT 光子事件概率理论模型
图1 所示为PMT 输出电子流脉冲堆叠对光子事件鉴别的影响,图中绿色为信号光子,蓝色圆圈为PMT 倍增级产生的电子,蓝色曲线为电子组成的电子流脉冲,橙色实线为时间鉴别阈值,阈值与电子流脉冲上升沿的交点为光子事件鉴别时刻,光子事件以数字方波的形式输出.与GM-APD 为代表的传统单光子探测器不同,PMT 没有物理死区时间,能够响应所有入射的光子.PMT 输出为初始光电子经过多级倍增后产生的电子流,短时间内入射光子数量的不同会导致PMT 输出脉冲的幅值不同,PMT 最终输出信号的幅值是由多个电子流脉冲叠加产生,叠加后的信号脉宽和幅值都会发生变化,从而影响到信号光子事件的时间鉴别.
从图1 可以看出,当多个光子在短时间内接连到达时,PMT 输出的多个电子流脉冲会产生堆叠,并形成一个更大规模的电子流脉冲信号,信号幅值的增大导致脉冲上升沿前移.使用固定阈值鉴别法时,这种变化会在原有的光子事件鉴别时刻中引入额外的脉冲行走误差.
2.1 PMT 光子探测概率模型
根据传统激光雷达方程,探测器接收到的单脉冲平均回波信号光子数Ns为
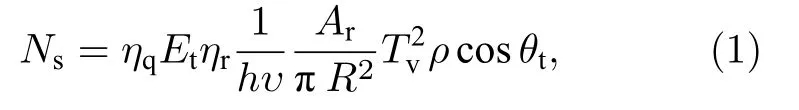
其中,Et是激光器单脉冲能量,h为普朗克常数,υ为激光频率,hυ为单个光子能量,Ar为接收光学天线口径,ηr为光学系统效率,ρ为目标反射率,θt为激光发射天线指向角与目标表面法向方向的夹角,R是目标距离,Tv为激光雷达与目标之间的单程大气透过率,ηq为探测器的光子探测效率.当回波激光信号脉冲为高斯脉冲时,探测器接收到的信号光子在时域上的分布可以表示为

其中,δ为回波激光信号的高斯脉宽,tp为高斯脉冲均值.假设τ为时间飞行仪的时间分辨率,则在(t,t+τ)时间段内探测器接收到的平均有效回波信号光子数为[19]
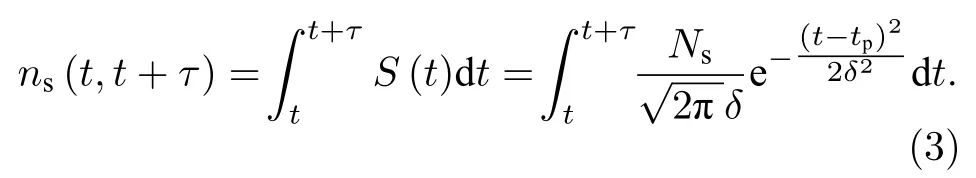
在传统单光子探测器模型中,当平均回波信号光子数为Ns,τ非常小时,单光子探测器在(t,t+τ)时间内探测到k个光子的概率满足泊松分布[20]:

其中,fn为噪声率.单光子探测器在(t,t+τ)时间内没有探测到光子的概率为

由于PMT 的光子探测过程没有物理死区时间的限制,可以响应每一个入射光子,所以PMT在第i个时间区间内的光子探测概率模型为
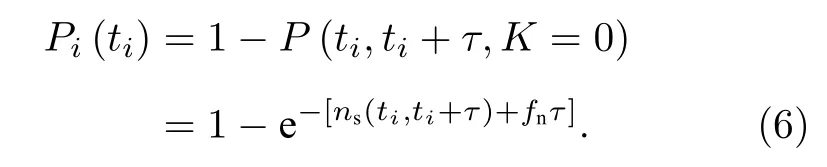
PMT 探测到的光子信号并不能全部被鉴别为光子事件,如图1 所示,不同的入射光子引发的电子流脉冲之间可能会发生堆叠,而PMT 光子事件鉴别电路无法分辨已经堆叠的脉冲,虽然PMT 探测到了多个光子,但是光子事件鉴别电路有可能只能输出一个数字脉冲,只代表一个可记录的光子事件,所以PMT 输出的光子事件概率并不等于光子探测概率.
2.2 PMT 光子事件概率模型
PMT 阴极表面接收到回波光子后会输出光电子,单个光电子通过多级倍增级放大,经过一定的渡越时间后输出一个电子流脉冲,电子流脉冲中的所有电子在时间上满足高斯分布[17],所以由单个光子引起的电子流脉冲函数可以表达为

其中,α为PMT 幅值系数,代表PMT 响应单光子输出电子流脉冲的峰值,δp为单光子电子流脉冲的高斯脉宽,µ0为电子流脉冲峰值时刻.对于某种特定的PMT 的电子渡越时间为固定值,为简化公式参数,假设由电子渡越时间引起的系统误差已被去除,使用电子流脉冲峰值时刻作为光子到达的真实时刻[21].
假设PMT 时间鉴别阈值为Th,PMT 输出的光子事件鉴别时刻tth满足:
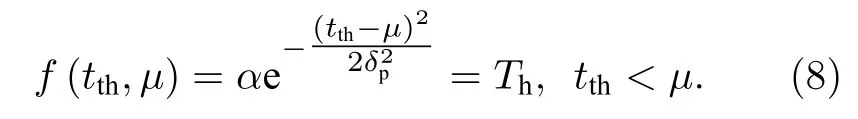
方程(8)具有唯一解.当回波光子数为1 时,如图2(a)所示,记PMT 输出的光子事件时刻与电子流脉冲峰值时刻的差值γ=µ-tth,在鉴别阈值确定的情况下,γ的值仅与所使用PMT 输出的单光子电子流脉冲的高斯脉宽δp有关.

图2 (a)回波光子数为1 时,PMT 光子事件鉴别时间与电子流脉冲峰值时间存在系统误差 γ ;(b)蓝色曲线和橙色曲线分别为PMT 响应 µ1 ,µ2 时刻到达的光子输出的电子流脉冲,黄色曲线为两个脉冲的叠加,为µ1,µ2时刻的电子流脉冲叠加产生的脉冲行走误差Fig.2.(a)When the number of incident photons is 1,there is a systematic error γ between the PMT photon-events identification time and the peak time of electron flow pulse;(b)the blue curve and the orange curve are the electron flow pulses output responsed by PMT for the photon arriving at time µ1 and µ2 respectively.The yellow curve is the pile-up of two pulses,and is the pulse walk error generated by the pile-up of the tow electron flow pulses at time µ1 and µ2 .
所以,当回波光子数为1 个时,PMT 在第i个时间区间鉴别到光子事件的概率为
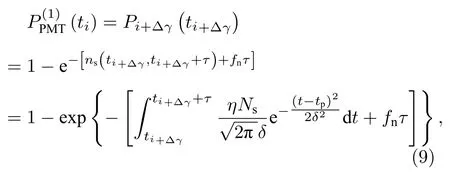
其中,Δγ=(向下取整),对比(6)式与(9)式可以看出,当回波光子数为1 时,PMT 输出光子事件时间区间比实际探测到光子的时间前移了Δγ个时间区间,从图2(a)可以看出,该前移量为系统误差,可以通过标定去除.
当回波光子数等于2 时,PMT 会响应两个光子并产生两个电子流脉冲,最终输出为两个电子流脉冲的叠加:

其中,µ1,µ2为先后两个电子流脉冲的峰值时刻µ1≤µ2.假设两个电子流脉冲时间间隔很小,鉴别电路无法分辨,则PMT 输出的光子事件鉴别时刻tth 满足:

此时PMT 输出的光子鉴别时刻与第1 个电子流脉冲的峰值时刻µ1的差值由系统误差γ和脉冲行走误差组成,如图2(b)所示.
当入射光子数为2 时,PMT 光子事件时间鉴别时刻tth可以表达为

所以,当回波光子数为2 个时,PMT 在第i个时间区间内鉴别到光子事件的概率可以表示为

其中mτ为电子流脉冲叠加引起行走误差,τ为光子事件计数器时间分辨率,Δt2为两个光子同时到达时电子流脉冲叠加产生的脉冲行走误差,p(2)(mτ)为两个电子流脉冲叠加引起的脉冲行走误差为mτ的概率.所以当回波光子数为2 时,对比(6)式与(13)式,PMT 输出的光子事件时间区间相对于实际探测到光子的时间前移了 Δγ+个时间区间,其中除了系统误差 Δγ以外,还存在脉冲行走误差.
同理,当回波光子数等于n个时,PMT 的光子事件概率可以表示为

其中,Δtn为n个光子同时到达时电子流脉冲叠加产生的脉冲行走误差,p(n)(mτ)为回波光子数为n时,n个光子事件脉冲叠加引起的脉冲行走误差为mτ的概率.
假设回波激光信号全部集中在(tp-3δ,tp+3δ)内,PMT 的总体光子事件概率模型可以表示为

从(15)式可以看出,PMT 光子探测过程中不受死区时间限制,但受电子流脉冲叠加的影响,叠加的脉冲将光子事件时刻提前,导致阈值鉴别时刻早于光子真实到达的时刻.PMT 光子鉴别时刻和光子到达时刻存在着系统误差 Δγ和由脉冲堆叠造成的随机误差,其中系统误差可以通过后期标定去除.但脉冲堆叠的随机过程非常复杂,无法用解析式表达,本文通过蒙特卡罗仿真研究脉冲堆叠对光子计数法测距的影响.
3 蒙特卡罗仿真
蒙特卡罗仿真流程:
1)生成符合泊松分布的nsp个信号光子和nnp个噪声光子;
2)根据(3)式,按正态分布生成信号光子时间标签,根据设定的噪声率按均匀分布产生噪声光子时间标签;
3)产生的所有时间标签按照(1)式生成PMT电子流脉冲函数,再按照(11)式计算叠加之后的脉冲函数;
4)根据设定的阈值计算光子事件鉴别时间;
5)按照设定的仿真次数重复上述1)-4)步骤.
仿真条件: PMT 输出脉宽为3.8 ns,激光脉冲脉宽为1 ns,时间分辨率τ为200 ps,噪声率fn为50 kHz,时间鉴别阈值0.5α,仿真次数为20000.
实验使用的PMT 型号为R9880U,单个光子入射时,其电子流脉冲高斯脉宽为3.8 ns,PMT 光子事件鉴别阈值设为0.5α,在该条件下进行蒙特卡罗仿真,仿真次数20000 次,本文提出的PMT光子探测模型与传统单光子探测理论模型的区别如图3 所示(已剔除系统误差 Δγ).
图3 中蓝色曲线为蒙特卡罗仿真PMT 探测模型的探测概率分布,橙色虚线为不考虑输出脉冲叠加的传统单光子探测模型的理论探测概率分布,绿色实线为参考基准位置.从图3 可以看出,当入射光子数较多时,PMT 的光子鉴别时刻直方图相对于传统单光子探测理论模型有明显的前移.因为信号光子数越多,PMT 输出脉冲叠加的概率越大,导致探测概率分布上两种模型的区别越明显.当入射光子数为10 个时,两个模型之间的时间重心差值差可达到1.7 ns,在高精度测距应用中,该误差不可忽略.
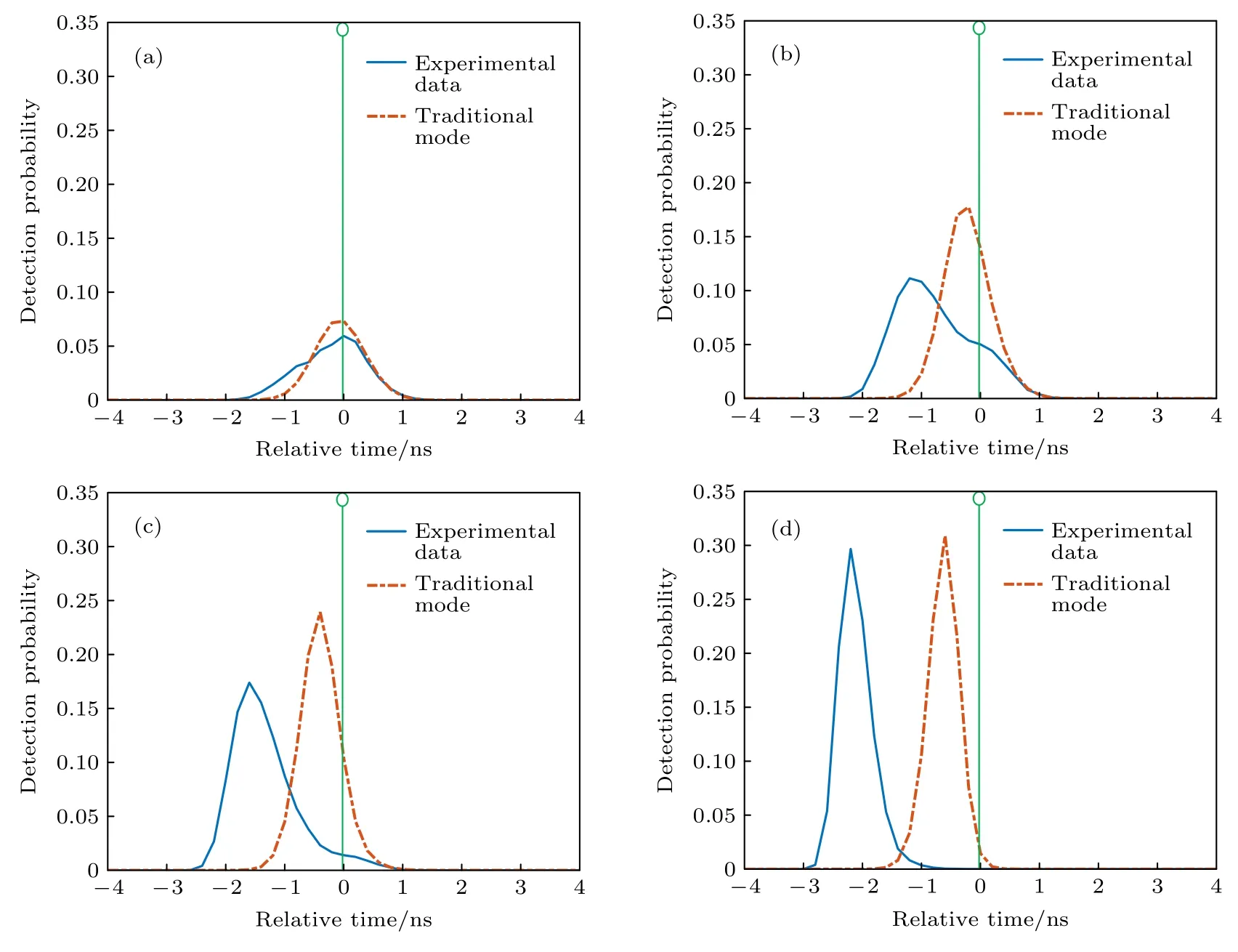
图3 PMT 单光子探测模型与传统单光子探测模型概率分布的区别(a) Ns=0.5;(b) Ns=2;(c) Ns=4;(d) Ns=10Fig.3.Difference of probability distribution between PMT single-photon detection model and traditional single-photon detection model:(a) Ns=0.5;(b) Ns=2;(c) Ns=4;(d) Ns=10.
为进一步研究脉冲堆叠对光子计数法激光测距的影响,用Ra表达光子计数法测距的行走误差,Rp表达光子计数法测距的精度[22]:

其中ntotal为距离门内时间区间的总数.
3.1 回波激光脉宽 δ 对PMT 光子计数法测距的影响
保持PMT 单光子电子流脉冲高斯脉宽δp不变,鉴别阈值Th=0.5α,通过蒙特卡罗仿真研究PMT探测模型的测距行走误差Ra、测距精度Rp与回波激光脉宽δ之间的关系,如图4 所示.
从图4 可以看出,随着回波激光脉冲高斯脉宽δ的增大,PMT 光子探测模型和传统单光子探测模型的测距行走误差Ra增大,测距精度Rp变差.考虑脉冲堆叠的PMT 探测模型相比于传统单光子探测模型,行走误差更大,由此导致测距精度的下降.特别是当回波激光脉冲脉宽远小于PMT 输出脉冲脉宽时(δ≪δp),两种模型Ra和Rp存在非常明显的差异,当δ=0.5 时,两种模型的Ra差值最大能达到22 cm.因为当回波激光脉冲脉宽特别小时,PMT 输出脉冲脉宽远大于回波激光脉宽,回波信号光子到达时刻分布集中,不同信号光子之间时间间隔小,相应的PMT 输出脉冲堆叠产生的测距行走误差的期望值大,方差小;反之在激光回波脉宽较宽时,回波信号光子到达时刻比较分散,不同信号光子之间时间间隔变大,PMT 输出脉冲叠加产生的测距行走误差的期望值小,方差大.综上所述,回波激光脉冲脉宽越小,PMT 探测模型测距行走误差越小,精度越高,但是 PMT 探测模型和传统模型的测距结果差异越大,这种情况下,不能使用传统模型代替PMT 探测模型.

图4 PMT 单光子探测模型和传统单光子探测模型关于测距行走误差Ra 和测距精度 Rp 的比较Fig.4.Comparison between PMT single-photon detection model and traditional single-photon detection model on ranging walking error Ra and ranging accuracy Rp.
3.2 PMT 单电子响应脉宽 δp 对PMT 光子计数法测距的影响
保持回波激光高斯脉宽δ不变,鉴别阈值Th=0.5α,使用蒙特卡罗仿真研究PMT 探测模型的测距行走误差Ra、测距精度Rp与PMT 单光子电子流脉冲高斯脉宽δp之间的关系.
图5 所示为PMT 探测模型测距行走误差Ra、测距精度Rp和回波光子数、PMT 单光子电子流脉冲函数高斯脉宽δp的关系.从图5 可以看出,δp越大,则PMT 探测模型的测距行走误差Ra越大,测距精度Rp越差.因为PMT 单光子电子流脉冲脉宽越宽,脉冲叠加导致的时间鉴别行走误差的期望值越大,对PMT 探测模型的Ra和Rp影响越明显.图5 中绿色曲线为不受脉冲叠加影响的传统单光子探测模型的测距行走误差Ra、精度Rp与信号光子数的关系.当电子流脉冲脉宽δp较小时,两种模型的Ra和Rp曲线比较接近,可见减小PMT输出脉冲脉宽δp可以有效减小脉冲堆叠引起的行走误差.

图5 不同电子流高斯脉宽 δp 条件下PMT 探测模型测距行走误差Ra 和测距精度 Rp 与入射信号光子数的关系Fig.5.Relationship of ranging walk error Ra and ranging accuracy Rp of PMT detection model to incident signal photon number under different Gaussian pulse width δp of electron flow.
3.3 光子事件鉴别阈值对PMT 光子计数法测距的影响
保持PMT 单光子电子流脉冲函数高斯脉宽δp、回波激光高斯脉宽δ不变,使用蒙特卡罗仿真研究PMT 探测模型的测距行走误差Ra、精度Rp与PMT光子事件鉴别阈值Th之间的关系,如图6 所示.
从图6 可以看出,随着鉴别阈值的不断增大,PMT 探测模型中的测距行走误差Ra不断增大,测距精度Rp不断下降,图6 中绿色曲线代表传统单光子探测模型的Ra和Rp曲线.随PMT 光子事件鉴别阈值的减小,PMT 的Ra和Rp曲线与传统单光子探测模型比较接近,说明较低的阈值能够减小PMT 输出脉冲叠加引起的测距行走误差.但在实际应用中,过低的阈值会使PMT 在光子探测中更容易受自身暗电流的影响,导致暗计数增多,反之提高鉴别阈值能够减弱暗电流的影响,减小暗计数,但是会增大PMT 测距行走误差,降低测距精度.
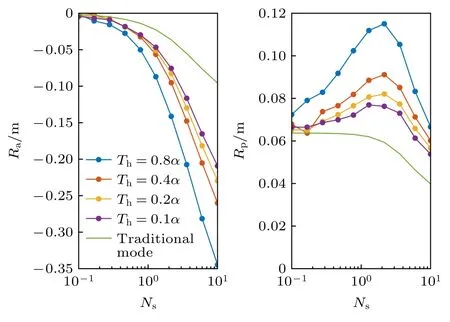
图6 PMT 探测模型测距行走误差Ra 和测距精度 Rp 与光子事件鉴别阈值 Th 的关系Fig.6.Relationship of the ranging walking error Ra and ranging accuracy Rp of the PMT detection model to the identification threshold of photon-events.
通过仿真分析,发现在以PMT 为探测器的光子计数激光雷达的应用中,PMT 电子流脉冲堆叠对测距精确度和测距正确度都有很大影响,当PMT 输出的电子流脉冲脉宽越宽,测距精确度和测距正确度就越低;同时光子事件鉴别阈值对光子计数法测距也有一定的影响,鉴别阈值越高,测距的精确度和测距正确度就越低.在实际应用中,为了提高PMT 光子计数法测距的精密度,需要选用激光脉冲尽可能窄的激光器;选用输出电子流脉宽尽可能窄的PMT,同时在保证光子探测信噪比的前提下,设置较低的鉴别阈值,以有效提升PMT光子计数法激光测距的精确度和正确度.
4 实验验证
为了验证PMT 输出电子流脉冲堆叠对光子计数法激光测距的影响,搭建了一套激光雷达实验系统,整个实验系统架构见图7,半导体激光器(laser)型号为NPL64B,出射激光波长为640 nm,均方根脉宽为4 ns,激光器驱动(laser driver)驱动激光器出光,激光器出射激光经分束镜(beam splitter)分束后一路入射到光电二极管(PIN)中,光电二极管响应后产生的电信号作为时间飞行仪(TDC)的STRAT 信号,另一路通过可调衰减片(adjustable ND filter)和固定衰减片(ND filter)衰减后通过光学发射天线发射,可调衰减片用于控制回波信号光子数.目标反射回波经光学接收天线收集后,由光线导入PMT 中,PMT 输出的数字信号作为时间飞行仪的STOP 信号,时间飞行仪的型号为MCS6A,时间分辨率为200 ps,计时精度为45 ps.

图7 光子计数雷达系统示意图Fig.7.Schematic of the photon-counting radar system.
为了确定实验中PMT 实际接收到的平均信号光子数,每次调节完可调衰减片后先不在光路中加入固定衰减片,使用高增益高精度APD 探测器模块(HAMAMATSU-C12702-11)对回波信号光子数进行估算,回波信号光子数满足以下公式[18]:

其中,h为普朗克常数,v为光子频率,Sv为光子频率为v时APD 的灵敏度,M为APD 增益,tAPD为APD 输出脉冲的脉宽,Vmax为APD 输出脉冲 峰值.在估算出信号光子数后再在光路中加入固定衰减片(OD3),将回波信号光子数衰减至单光子量级.
为了验证单光子电子流脉冲函数高斯脉宽对PMT 探测的影响,在实验中使用了两种阈值鉴别电路.图8(a)为无放大器的光子事件鉴别电路,采用8 GHz 带宽的差分比较器对PMT 的输出信号进行直接鉴别,P 端为PMT 的信号输出端,DY端为PMT 最后一级倍增级偏置电压,通过差分比较器能减小电源噪声对信号探测的影响.差分比较器输出信号格式为LVCML,经过脉冲整形器整形后转换为TTL 电平后能直接被时间飞行仪识别,该电路没有对PMT 原始信号进行处理,PMT单电子响应脉宽不变.图8(b)为带射频(RF)放大器的光子事件鉴别电路,与图8(a)的主要区别是采用了差分射频放大器对PMT 输出信号进行放大.由于放大器的带宽限制,放大后的PMT 电子响应脉宽从3.8 ns 展宽为6 ns,在经过比较器和整形器后输出鉴别信号至时间飞行仪中.通过两种不同光子事件鉴别电路探究PMT 单光子电子流脉冲脉宽对单光子测距的影响.

图8 (a)无射频放大器光子事件鉴别电路;(b)带射频放大器光子事件鉴别电路Fig.8.(a)Photon-events identification circuit without RF amplifier;(b)photon-events identification circuit with RF amplifier.
首先使用4 ns 脉宽的激光器进行测距实验,为减小背景噪声影响,实验在暗室中进行,背景噪声率为50 kHz.图9(a)为示波器(MSO4104)测得的PMT 原始电子流脉冲信号归一化幅值和平均入射信号光子数之间的关系,可以看出,随着入射光子数的增多,脉冲上升沿逐渐前移.APD 探测器模块(HAMAMATSU-C12702-11)接收到的回波信号波形如图9(b)所示,回波激光信号脉冲的上升沿时间为2.10 ns.

图9 (a)PMT 输出脉冲归一化幅值与平均入射信号光子数的关系;(b)APD 测得的回波信号脉冲Fig.9.(a)Relationship between PMT output pulse normalized amplitude and average number of incident signal photon;(b)incident signal pulse measured by APD.
加上固定衰减片和可调衰减片后,使用带RF放大电路的PMT 模块、不带RF 放大电路的PMT模块(两种模块使用的PMT 裸管型号均为R98 80U),以及GM-APD(SPCM50A/M)进行信号探测,所使用的两种单光子探测器的主要性能参数如表1 所列,两种探测器探测效率大致相同.值得注意的是,表1 中PMT 的探测死区时间是由脉冲整形电路中锁存器造成的,PMT 本身没有光子探测死区时间.最终测距实验结果如图10 所示.
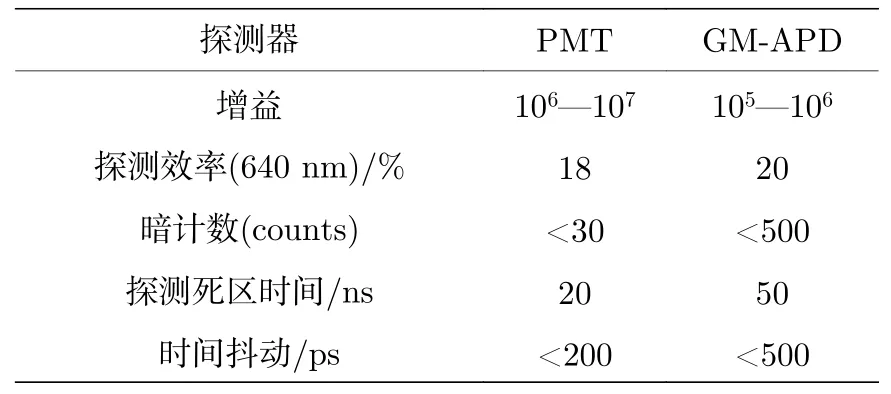
表1 PMT 和GM-APD 模块性能参数Table 1. Parameters of PMT and GM-APD module.
实验中设置激光器重频为1 MHz,时间飞行仪累计时间为1 s,图10 中蓝色曲线为通过时间飞行仪输出结果计算而来的单光子探测概率,橙色虚线为传统单光子探测理论模型的探测概率,绿色实线为以目标实际距离为零点基准位置.对比图10(a)和图10(c)与图10(b)和图10(c)可以看出,由于PMT 输出脉冲叠加效应的影响,相比于GM-APD的探测概率和单光子探测理论模型,两种PMT 实际的探测概率有较为明显的前移,而且随着入射光子数的增多,时间重心的前移量越明显.这是因为当入射光子数较多时,PMT 在短时间响应多个光子的概率增大,电子流堆叠的概率就会变大,脉冲行走误差导致整个时间累计直方图前移.对比图10(a)和图10(b)可以看出,PMT 单光子电子流脉冲高斯脉宽δp越宽,探测概率直方图前移越明显,证明当激光脉宽不变时,随着δp越大,PMT 测距行走误差Ra越大.
为进一步验证理论的正确性,将激光脉宽仿真参数改为4 ns,与实验使用激光器脉宽相同,并使用图10(a)和图10(b)的实验环境参数和电路硬件参数重新进行蒙特卡罗仿真,仿真结果如图11 所示.

图10 (a)带RF 放大器的PMT 探测概率分布随入射信号光子数的变化;(b)不带RF 放大器的PMT 探测概率分布随入射信号光子数的变化;(c)GM-APD 探测概率分布随入射信号光子数的变化Fig.10.(a)Experimental results of PMT detection probability distribution with RF amplifier varying with the number of incident signal photons;(b)experimental results of PMT detection probability distribution without RF amplifier varying with the number of incident signal photons;(c)experimental results of GM-APD detection probability distribution varying with the number of incident signal photons.

图11 (a)带RF 放大器的PMT 探测概率分布随入射信号光子数的变化仿真实验结果;(b)不带RF 放大器的PMT 探测概率分布随入射信号光子数的变化仿真实验结果Fig.11.(a)Simulation results of PMT detection probability distribution with RF amplifier varying with photon number of incident signal;(b)simulation results of PMT detection probability distribution without RF amplifier varying with photon number of incident signal.
图11 中蓝色曲线为通过蒙特卡罗仿真计算得到的单光子探测概率分布曲线,橙色虚线为传统单光子探测理论模型的探测概率曲线.对比图11(a)和图11(b)与图10(a)和图10(b),蒙特卡罗仿真结果和实验结果基本相符,都是随着入射光子数增多,PMT 的探测概率分布和传统模型的差异逐渐增大.唯一区别是当入射光子数Ns=0.5 时,图11中PMT 光子探测模型和传统光子探测模型探测概率曲线几乎没有差异,而图10 中两种模型探测概率曲线存在一定差异.原因是蒙特卡罗仿真过程和传统单光子模型计算过程中,均假设激光脉冲时域分布严格满足高斯函数,而实际实验时使用的激光器出射激光经目标反射后的回波激光脉冲时域分布并不是严格的高斯函数,而是上升沿较快,下降沿有一定的拖尾的近高斯函数,所以才导致蒙特卡罗仿真结果和实验结果有一定的差异.但总体来说,实验结果和仿真结果实基本相符,证明了PMT输出电子流脉冲堆叠对光子计数法测距影响理论分析的正确性.
图12 中实线为蒙特卡罗仿真结果的行走误差曲线,离散点为实验结果的行走误差数据点,可以看出由于GM-APD 存在物理意义上的死区时间,在探测到一个光子事件后立即被淬灭,所以GMAPD 输出单光子信号脉冲不会有叠加的现象产生,光子事件鉴别时刻不受脉冲幅值变化的影响,测距行走误差最小.对于PMT,其单光子电子流脉冲脉宽越宽,时间相近的信号脉冲叠加后产生的脉冲行走误差越大,所以带RF 放大器的PMT 测距行走误差要高于不带RF 放大器的PMT.在基于PMT 光子的光子计数雷达应用中,为提高测距精度和准度,降低脉冲堆叠行走误差的影响,需尽量选择使用输出脉冲脉宽较窄的PMT.
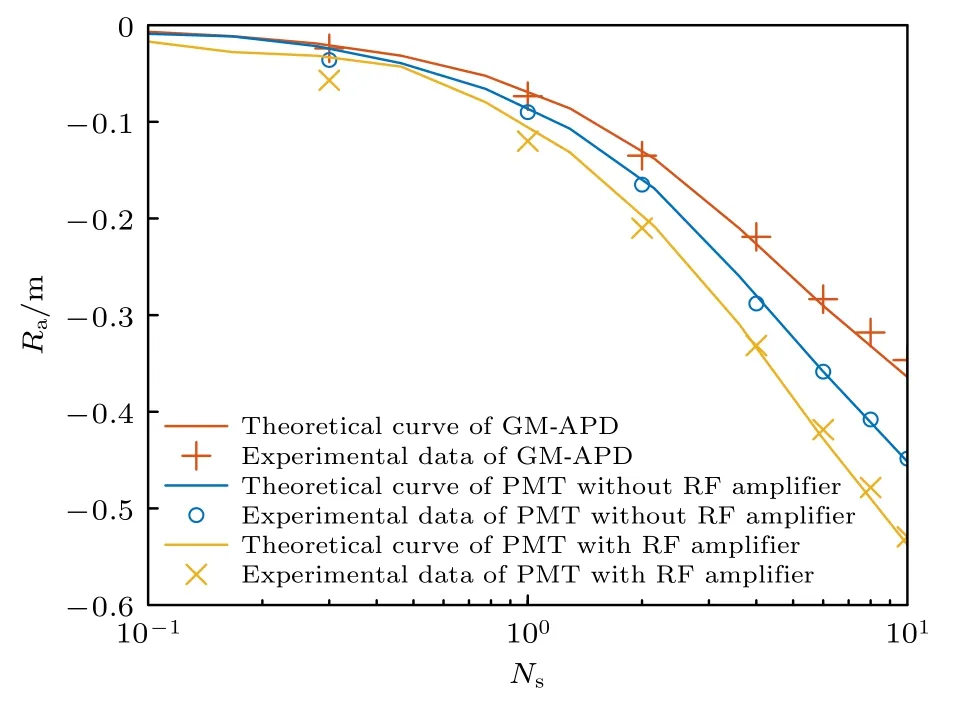
图12 三种探测器的测距行走误差的仿真模型和实验数据对比,橙色实线为GM-APD 的Ra 理论探测曲线,橙色“+”为GM-APD 的Ra 实验数据点;蓝色实线为不带放大器PMT 的Ra 理论探测曲线,蓝色“o”为不带RF 放大器的PMT的 Ra 实验数据点;黄色实线为带RF 放大器PMT 的Ra 理论探测曲线,黄色“x”为带RF 放大器PMT 的Ra 实验数据点Fig.12.Comparison of the simulation model and experimental data of the ranging walking error of the three detectors.The solid orange line is the Ra theoretial curve of GM-APD,and the orange “+” is the Ra experimental data point of GM-APD.The blue solid line is the Ra theoretial curve of PMT without RF amplifier,and the blue “o” is the Ra experimental data point of PMT without RF amplifier.The solid yellow line is Ra theoretial curve of PMT with RF amplifier,and the yellow “x” is Ra experimental data point of PMT with RF amplifier.
5 结论
PMT 光子探测过程不同于GM-APD,没有物理意义上的光子探测死区时间,所以当光子接连入射到PMT 光敏面时,PMT 产生的单光子电子流脉冲会在PMT 最终输出端堆叠为幅值更高的脉冲信号,脉冲幅值的变化会在光子事件鉴别过程中引入新的脉冲行走误差.本文详细分析了脉冲堆叠对PMT 光子探测的影响,并建立新的模型描述PMT 的光子事件探测概率.通过蒙特卡罗仿真PMT 的光子探测过程发现,由于脉冲行走误差的影响,PMT 的光子事件探测概率直方图相对于传统单光子探测模型会有明显的前移,意味着在脉冲行走误差的影响下,使用PMT 作为探测器的单光子激光雷达测距的行走误差更大,测距精度也更差.通过仿真还发现PMT 单光子电子流脉冲脉宽,回波信号脉宽和时间鉴别阈值都会影响PMT 的探测概率,单光子电子流脉冲脉宽越宽,回波激光脉宽越宽,鉴别阈值越高,测距行走误差越大,测距精度越差.为了验证理论模型和蒙特卡罗仿真的正确性,论文中搭建了一套单光子激光测距系统,通过使用不同输出脉宽的PMT 和不同出射激光脉宽的激光器进行实验,实验结果与GM-APD 结果进行对比,结果发现随着激光脉宽的增大,PMT输出电子流脉冲脉宽的增大,单光子激光测距系统的测距行走误差越大,测距精度越差;同时将PMT 的测距结果和GM-APD 结果进行对比,发现PMT 光子探测概率统计直方图和传统单光子探测模型的确存在区别,实验结果与理论结果基本吻合.本文通过实验验证了PMT 光子探测模型的正确性,证明了脉冲堆叠对PMT 的光子探测过程有明显影响.
本文提出的PMT 光子探测模型指出了PMT输出电子流脉冲堆叠会影响光子计数法测距的精度和准度,增大测距行走误差,在对测距精确度要求特别高的场合中,使用PMT 作为探测器时,这种影响不可忽略,通过理论模型发现,使用窄激光脉冲的激光器,减小PMT 输出电子流脉冲的脉宽,以及尽可能的降低PMT 时间鉴别阈值都能明显提升单光子测距系统的测距性能.所以本文的PMT光子探测理论模型和仿真结果对基于PMT 的光子计数雷达系统的设计,相关器件参数的选择,以及分析系统测距误差,提高系统测距精度和准度具有重要的指导意义.
