基于特征谱线与约束拟合相位的绝对波数标定方法*

王迪 韩涛 钱黄河 刘智毅 丁志华

(浙江大学光电科学与工程学院,现代光学仪器国家重点实验室,杭州 310027)

谱域光学相干层析成像(spectral-domain optical coherence tomography,SD-OCT)系统中普遍存在波数域的非线性采样问题.为实现常规快速傅里叶变换算法下离散界面的精确定位与OCT 图像的高质量重建,需要解决光谱仪中离散采样点绝对波数的精确标定问题.本文提出了一种基于精确光程差下特征谱线与约束拟合相位的绝对波数标定方法,在谱域OCT 系统的样品臂中,使用具有精确厚度差异的金属量规,获得特征谱线对应的绝对相位值,进一步精确求解出特征谱线对应的相位包裹次数,克服了常规干涉光谱相位方法中普遍存在的2π 歧义,结合窗口约束条件下高信噪比区域的拟合相位,实现光谱仪采样点绝对波数的精确标定.通过全面比较本文方法与传统插值重采样方法在离散界面定位、轴向分辨率以及图像重建质量等方面的差异,验证了本方法的显著优势.

1 引言

光学相干层析成像(OCT)[1,2]是一种基于低相干干涉原理的三维断层成像技术,可以实现生物组织内部微米量级的高分辨率实时成像,也可用于材料的无损检测与精细结构的三维重建[3-7].谱域OCT 技术是当前应用最为广泛的OCT 成像技术,通过光栅光谱仪探测并采集干涉光谱信息,相对于时域OCT 技术具有显著的信噪比、灵敏度和成像速度优势[8-10].

谱域OCT 技术中,波数域与深度域是傅里叶变换关系.对干涉光谱信号进行傅里叶变换,可以得到沿深度方向分布的反射系数,反映了样品深度方向的结构信息.由于光栅光谱仪色散分光原理,谱域系统中普遍存在非线性采样问题,具体表现为在线阵探测器等像素间隔位置上,采集的干涉光谱在波数域上的分布不均匀.为满足传统快速傅里叶变换(fast Fourier transform,FFT)算法对波数域均匀采样的要求,需要对干涉光谱信号进行插值重采样,以获得波数域上均匀分布的干涉光谱[11],从而避免轴向点扩散函数的展宽以及灵敏度快速下降[12].而且,获得均匀分布光谱的绝对波数值,可以实现深度域位置信息的精确定位.因此,光谱仪绝对波数的标定是实现谱域OCT 系统中离散界面精确定位及高信噪比、高轴向分辨率OCT 图像重建的前提.Hu 和Rollins[13]首次在谱域系统中引入线性波数光谱仪,Wu 等[14]在此基础上进行了光谱仪结构参数的优化,从而实现了均匀波数采样,但不可避免地提升了硬件结构复杂度.Hyle Park 等[15]提出了基于光谱仪物理模型的标定方法,结合具体几何参数计算各像素点的对应波长,但理论推导过程极为复杂.特征谱线多项式拟合方法是经典的波长标定方法,这类方法基于标准定标光源或物质的特征吸收光谱,可以建立波长-采样像素对应关系,如Perret 等[16]利用法布里-珀罗干涉滤光片的等间距谱线,Eom 等[17]利用布拉格光栅的多条特征谱线,最终通过多项式拟合获得采样空间的波数标定结果,但这类方法仍受制于特征谱线数量、线宽以及分布情况.基于干涉光谱相位的波数标定方法无需额外硬件,通过计算特定光程差下干涉光谱相位与波数间的线性关系,可以实现光谱仪的标定,如Wang 和Ding[18]基于两次干涉光谱相位相减方法消除色散影响,实现了光谱仪均匀分布波数的重采样,但尚未考虑相位噪声对波数标定的负面影响,而且,该方法无法直接确定采样点的绝对波数.Wu 等[19]在共路谱域OCT 系统样品臂中,使用不同厚度的金属量规,求解第一个采样像素的初始相位值,结合相对相位分布,恢复采样空间的绝对相位,但其初始相位值的求解存在较大误差,同时绝对相位中混入大量的相位噪声,无法实现绝对波数的求解.

本文提出了一种基于精确光程差下特征谱线与约束拟合相位的绝对波数标定方法,在谱域OCT系统的样品臂中使用具有精确厚度差异的金属量规,准确求解特征谱线对应的绝对相位值的包裹次数,克服了常规干涉光谱相位方法中普遍存在的2π 歧义,并结合窗口约束条件下高信噪比区域的相位拟合,实现了采样点空间绝对波数的精确标定.通过全面比较所提方法与传统重采样方法在离散界面定位、轴向分辨率以及图像重建质量等方面的差异,验证了本方法的显著优势.

2 理论方法

不失一般性,谱域OCT 系统探测得到单层离散反射面的干涉光谱信号,去除直流项和自相关项后可表示为

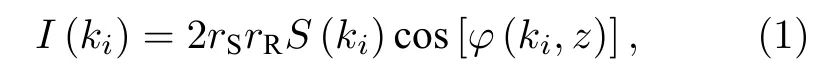
式中,ki为光谱仪采集的离散波数,i=1,2,···,N表示采样序列;rS和rR分别表示参考反射面和样品反射面的反射系数;S(ki)为光源功率谱分布函数;z为反射面与参考面光程差的一半;φ(ki,z)为对应的光谱域绝对相位离散分布,可以用非线性采样函数g(k)=ki与两干涉臂间不平衡色散项h(ki)来表示

其中,k为波数.对(1)式实施希尔伯特变换,可以得到限制在 [-π,+π] 主值区间内的包裹相位分布φw(ki,z)[20,21]:

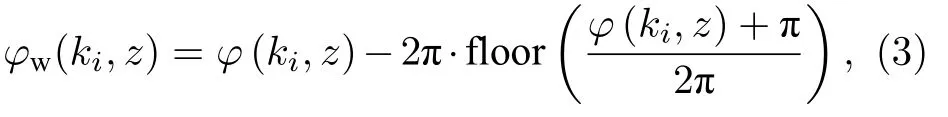
式中,floor 表示向负无穷方向取整运算,不同的离散采样波数ki有不同次数的相位包裹,存在 2π 歧义,即相位卷绕问题[22].

以起始采样点为基准对包裹相位φw(ki,z)做连续化解包裹处理,可以得到相对相位分布,但一般的干涉光谱中心区域信噪比高(相位噪声小)、边缘区域信噪比低(相位噪声大),边缘区域的相位噪声将在连续化解包裹过程中累积放大,从而影响恢复相位的准确性.因此,可采用以临近中心位置kc的相位主值作为起点的双向连续化解包裹处理,得到相对相位分布φr(ki,z):

式中,N=为固定值,表示临近中心位置(对应波数kc)的相位包裹次数.为消除(2)式中两干涉臂间的不平衡色散,采集不同光程下两组干涉信号并分别提取相位,进而获得精确光程差(2Δz=2(z2-z1))下对应的相位差分布:

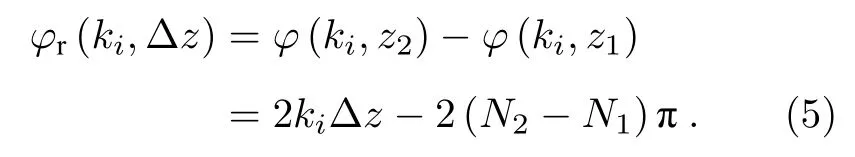
实际情况下,当特征谱线处于光谱仪临近中心区域时,可进行光谱仪精确标定.以He-Ne 激光特征谱线为例,对应的绝对相位为 2kHeNeΔz,可以计算出对应相对相位的包裹次数N2-N1,表示为

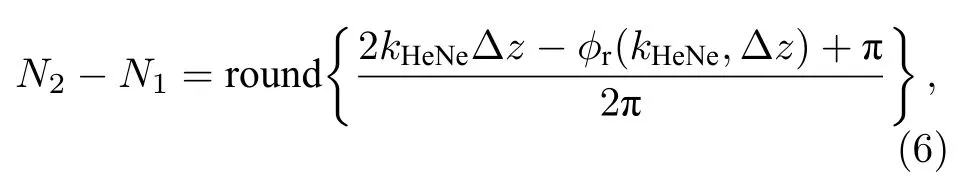
式中,round 运算表示取最接近的整数值,当特征谱线kHeNe与光程差 2Δz引入的误差相位不超过π时,可以求得准确的绝对相位包裹次数.由此恢复得到光程差 2Δz下所有采样光谱点的绝对相位分布为

考虑到相位噪声分布 δφ(i)对光谱采样的影响,实际系统得到的相对相位分布为=φr(ki,Δz)±δφ(i),与理论值具有一定偏差,最终影响绝对相位恢复结果以及波数标定的准确性.常见的基于全采样序列光谱相位φ-波数k的最小二乘多项式拟合方法,可以在一定程度上去除相位噪声的干扰,但不能避免中心区域相位的整体偏移.Han 等[23]在最小二乘拟合过程中,加入过中心采样点拟合的约束条件,改善了中心区域的相位偏移情况,但仍无法剔除边缘噪声的影响.因此,在最小二乘拟合过程中,加入拟合窗口约束条件,可以充分结合采样中心区域高信噪比、低相位噪声的特点,得到更接近高信噪比相位理论分布的拟合相位.在采样中心区域加入窗口宽度为 2L的约束条件,进行绝对相位φa(ki,Δz)的部分拟合,可以求得最小二乘多项式的拟合系数{c0,c1,c2,c3,...},并以此恢复得到对应光程差 2Δz下的全采样序列拟合相位:

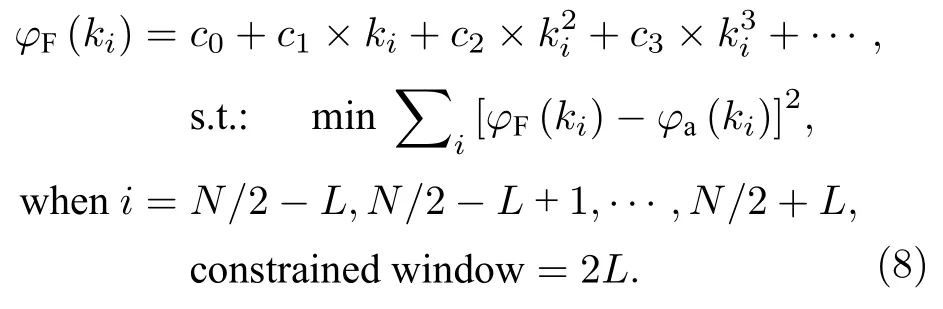
最小二乘拟合算法获得的均方偏差会随着窗口约束条件 [N/2-L,N/2+L] 的改变而改变,通过比较不同约束条件下,高信噪比区域的相位均方偏差值,最终可以确定最佳窗口约束拟合条件.此时获得的拟合相位在高信噪比区域贴合于采样恢复相位,在采样边缘位置则符合光谱域相位平滑变化趋势,相比于恢复绝对相位φa(ki,Δz),更接近于理想相位分布.

在获得特征绝对相位的基础上,结合特征谱线波长数值,可以精确求解实际的精确光程差=φa(kHeNe,Δz)/kHeNe,继而用于精确绝对波数分布的标定.在最佳窗口约束相位拟合条件下,得到绝对波数分布,均匀化处理后获得重采样向量分布k＇[i],依次表达为

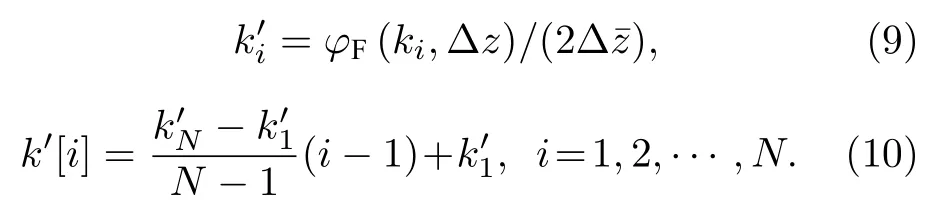
3 实验系统与标定过程

如图1 所示,在已有超高分辨谱域OCT 系统[24]基础上,本实验系统进行部分改进.超连续光源发出光谱带宽约为 200 nm 的可见低相干光,经2 倍扩束器扩束后,平行入射至分光比为1∶1 的分束器上(BS,Thorlabs),透射光部分经 30 mm 透镜聚焦到参考臂平面镜上,反射光部分则通过扫描振镜(GVS012,Thorlabs)扫描,经消色差透镜(f=30 mm,Edmund optics)聚焦到样品上;最终,两束返回光重新汇聚,经扩束、50 μm 小孔滤波后入射至衍射光栅上(600 线/mm,Wasatch Photonics),形成宽光谱色散,最终被像素数2048、行频250 kHz的线阵互补金属氧化物半导体相机(CMOS,OCT OPLUS,Teledyne E2v)采集,实现了最高250 fps(frames/s)成像速度(对应于横向1000 个采样点数)的快速成像.此外,引入基于He-Ne 激光器的特征谱线(632.8 nm)的光谱标定模块,并在样品臂成像位置处设置两组金属量规(量规厚度分别为d1=1350 μm ,d2=1250 μm,厚度偏差|δd|＜0.1 μm)作为高反射样品来实施光谱仪的波数标定.两组金属量规对应的双臂光程差分别为 2z1和2z2,且两量规的上表面位置对称分布于谱域OCT 系统的零光程附近,满足关系z1＜0＜z2.分别采集两组量规上表面与参考臂反射镜返回光的干涉信号,提取相位并通过相减获取光谱位相差,以消除色散失配.该光谱相位差分布可认为是由虚拟“空气隙”间的干涉所致,且虚拟“空气隙”的光程为量规的厚度差(2Δz=2(d1-d2))所导致.

图1 用于光谱仪标定实验的谱域OCT 系统Fig.1.Schematic diagram of the spectral domain optical coherence tomography system for spectrometer calibration.

根据(7)式求解光谱绝对相位及(6)式求解相位包裹次数的方法,在高信噪比相对相位值φr(kHeNe,Δz)确定的条件下,“空气隙”对应的绝对位相差分布的准确求解,依赖于设定光程差 2Δz和特征谱线值kHeNe的精确性.本实验选用国标量规标称值与实际值间存在不大于 0.1 μm 的厚度偏差,对应“空气隙”光程差小于 0.2 μm,由此造成的相位误差kHeNe·2δd≈0.63π＜π ;同时,由于本系统光栅光谱仪具有较高的光谱分辨能力(约 0.2 nm),由特征谱线偏差造成的相位偏差 δkHeNe·2Δz可以忽略不计.因此,结合特征谱线的绝对相位差标定方法,可以准确求解绝对相位差的包裹次数,并准确恢复“空气隙”对应的绝对相位差分布.同时,根据特征绝对相位恢复结果φa(kHeNe,Δz),结合特征谱线波长对“空气隙”实际光程进行反解,得到与标称值的光程偏差,满足标定要求.

图2 展示了利用He-Ne 特征谱线恢复“空气隙”绝对相位差的过程.图2(a)中He-Ne 激光特征谱线出现在CMOS 相机像素序列i=1025 处,其半高全宽小于一个像素间隔;图2(b)展示了两组金属量规样品对应的互相关干涉信号,红色与蓝色曲线分别对应了负光程差z1与正光程差z2下的干涉信号;依照前述方法处理获得正负光程下的连续化相对相位φr(ki,zi)如图2(c),两者呈现相反的变化趋势;最终,根据构造的“空气隙”相对相位φr(ki,Δz),结合(6)式计算得到“空气隙”对应的相位包裹次数为N2-N1=315,由此恢复的绝对相位曲线如图2(d)所示.

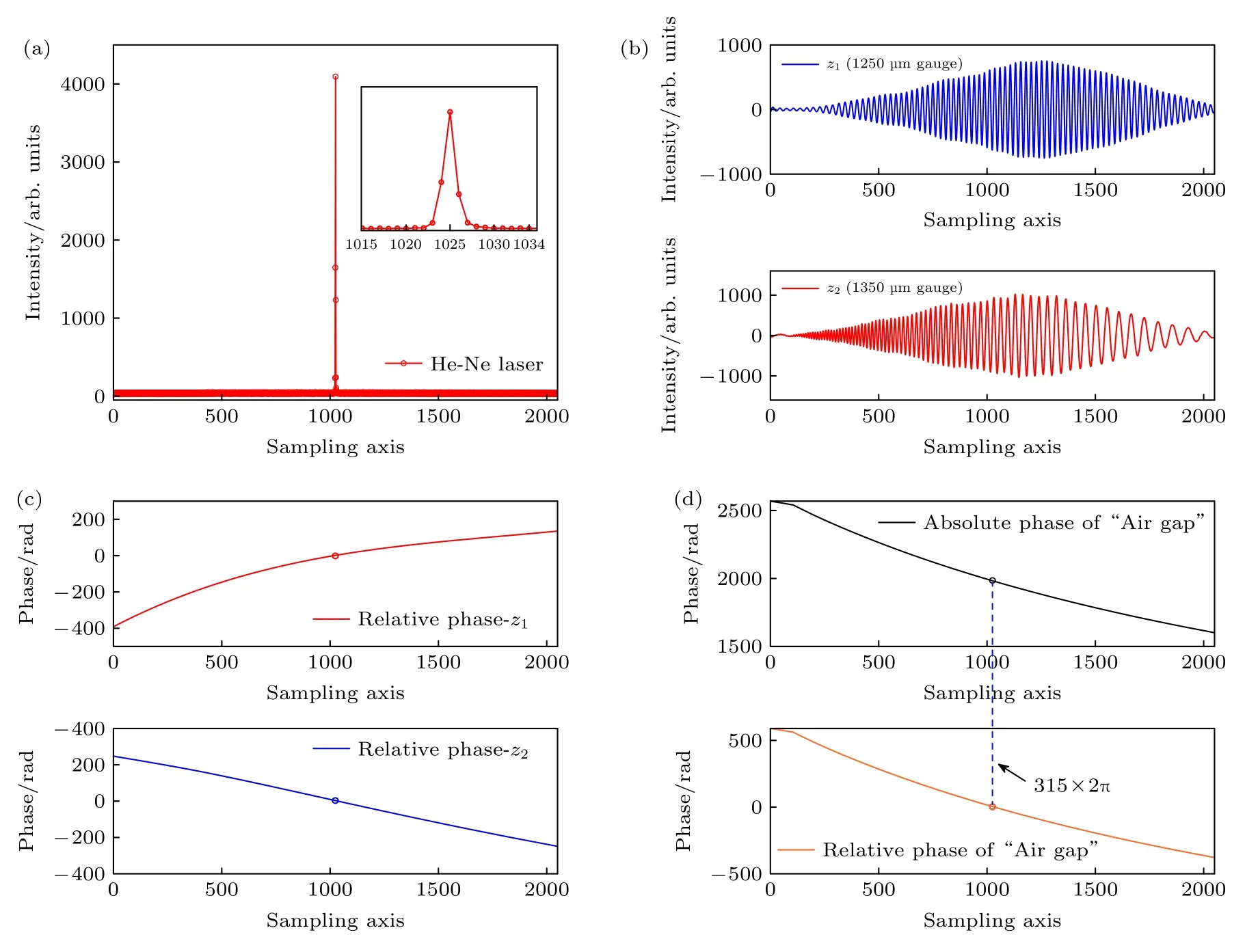
图2 He-Ne 特征谱线恢复“空气隙”绝对相位的过程(a)He-Ne 特征谱线标定光谱;(b)两组金属量规的互相关干涉信号;(c)连续化处理后的相对相位分布;(d)恢复的“空气隙”绝对相位分布Fig.2.Process of recovering the absolute phase of “air gap” from He-Ne characteristic spectral line:(a)Spectrum of He-Ne characteristic line calibration;(b)cross correlation interference signals of two groups of metal gauges;(c)relative phase distribution after continuity;(d)recovered absolute phase of “air gap”.

图3 展示了上述绝对相位φa(ki,Δz)的相位差波动,其中左边缘区域、中心区域以及右边缘区域的局域放大图分别用不同颜色的线框圈出;采样边缘区域相位波动大(可达 0.1 rad),具有较高相位噪声,而采样中心区域相位波动小(仅约 0.01 rad),对应了更高的信噪比,印证了本方法的可行性.

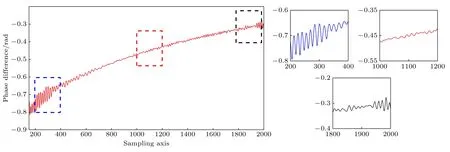
图3 “空气隙”采样绝对相位的相位差波动及不同区域相位差波动情况Fig.3.Phase difference fluctuations of absolute phase of “air gap” and phase difference fluctuations in different sampling regions.

在恢复采样绝对相位的基础上,控制窗口约束条件进行绝对相位的多项式拟合,获得平滑的拟合绝对相位分布.图4 展示了最佳窗约束条件下的拟合绝对相位,以及不同窗约束条件下的相位均方偏差大小.以中心采样点为拟合窗口中心位置,依次改变窗口宽度进行绝对相位最小二乘多项式拟合,得到了不同窗约束条件下拟合相位和恢复相位之间的相位均方偏差,图4(b)描述了相位均方偏差随约束窗口变化的规律,其最小值对应了最佳约束条件和最佳拟合窗口位置(拟合区域[216,1832]),由此得到的窗口约束下最佳拟合相位如图4(a)中所示,在边缘位置相位拟合曲线偏离采样相位值,反映算法对低信噪比区域的相位进行了拟合校正.最终,根据(9)式的计算过程,获得光谱仪采样空间的绝对波数分布.

图4 最佳窗口约束条件下的拟合绝对相位及不同窗约束条件下相位标准偏差分布曲线(a)最佳拟合绝对相位分布;(b)不同窗约束下相位标准偏差变化曲线Fig.4.Absolute phase fitting curve under optimum window constraints and phase standard deviation curve under different window constraints:(a)The optimal fitting of the absolute phase distribution;(b)phase standard deviation curve under different window constraints.

4 结果与讨论

4.1 离散反射界面的成像实验结果

基于最佳窗口约束条件获得的拟合绝对相位,可以用来计算采样轴上的绝对波数分布,继而得到线性化后的波数序列,以此为基础进行干涉光谱信号的重采样、消除色散及快速傅里叶变换,可以获得相比传统重采样方法更佳的成像结果.

图5 展示了谱域OCT 系统使用不同处理算法获得的轴向点扩散函数(PSF),包括直接快速傅里叶变换方法(direct FFT)、传统波数域插值重采样方法(k-domain spline interpolation without fit,KDSI),以及基于不同窗约束条件下相位拟合的插值重采样方法(window-constrainedk-domain spline interpolation,WC-KDSI),所有的点扩散函数均以本文提出方法(最佳窗约束条件下的WC-KDSI算法,WC-KDSI(Best fitting))的点扩散函数峰值为基准进行了归一化处理.其中,直接FFT 方法的轴向点扩散函数极大展宽,证明重采样以及消除色散过程具有必要性;传统的KDSI 算法进行了波数域的直接插值以及色散去除,其峰值信号强度及点扩散函数的半高全宽较直接FFT 方法有很大提高,但与WC-KDSI 方法相比则逊色不少;在最佳窗约束条件下,WC-KDSI 方法的轴向点扩散函数质量相较于其他窗约束条件也略有所提高.表1详细表述了上述各方法获得的离散界面点扩散函数的半高全宽及归一化强度差异,本文提出方法获得点扩散函数的半高全宽即轴向分辨率可达 1.6 μm,高于传统的KDSI 方法的 2.1 μm 及直接FFT方法的 5.3 μm,同时其归一化强度最大,深度域信号的信噪比更高.

图5 不同方法获得的轴向点扩散函数比较Fig.5.Axial PSFs obtained by different methods.

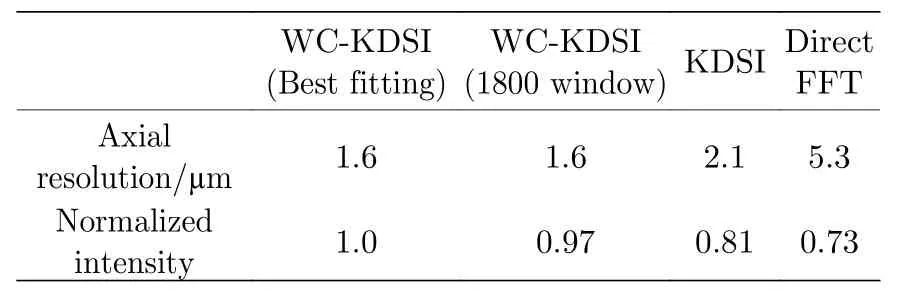
表1 不同方法获得的轴向分辨率和峰值归一化强度Table 1. Axial resolution and peak intensity resulted from different methods.

研究发现,传统KDSI 方法不仅在轴向点扩散函数的半高全宽、峰值强度上与本文提出方法具有一定差距,针对单反射面峰值位置的精确定位,也存在离散采样位置差异.为了验证所提出方法相较传统KDSI 方法在单界面精确光程定位上具有一定优势,对标定过程中金属量规“空气隙”的峰值离散位置和峰间离散采样间隔进行了定位.图6 中分别使用KDSI 方法和WC-KDSI 方法处理两金属量规离散界面的干涉信号,获得KDSI 方法下两量规峰间像素采样间隔为n3-n1=163 ,根据dz=π/(Ndk)=0.62 μm,可求实际光程差为OPDKDSI=2(n3-n1)dz=201.1 μm;同时,WC-KDSI 方法下两量规峰间采样间隔为n4-n2=162,对应实际光程差为 OPDWC-KDSI=2(n4-n2)dz=199.9 μm,实验中使用的两组量规具有精确的光程差为 200 μm,其预设误差小于 2δd=0.2 μm .显然,本文提出方法相较于传统的KDSI 方法在离散界面的精确定位方面,具有突出优势;进行光谱域信号多倍补零处理后,可以获得更小的深度域采样间隔,两种方法间的定位精度偏差将更加凸显.

图6 经KDSI 方法和WC-KDSI 方法处理得到的量规反射面定位结果Fig.6.Positioning results of gauges’ interfaces processed by KDSI method and WC-KDSI method.

4.2 镜面腐蚀部位的成像实验结果

为了实际说明提出方法在实际三维形貌重建方面具有一定优势,本文首先针对镜面腐蚀位置的微形貌特征进行了实际成像,分别使用直接FFT方法、KDSI 方法及WC-KDSI 方法处理了三维图像数据.处理获得的OCT 重建图像如图7 所示,图中选用了同一扫描位置的B-scan 进行展示,为了提高图像的信噪比,使用相邻10 幅B-scan 层析图像进行了实际处理[25].图7(a)中,镜面点扩散函数展宽,所得重建图像模糊,且三维重建结果不能分辨瑕疵细节;图7(b)及图7(c)分别使用KDSI方法及WC-KDSI 方法对表面腐蚀的微形貌进行了重建,腐蚀部分以及镜面部分均具有较高的信噪比,所得C-scan 均可以清晰分辨镜面腐蚀情况,但在腐蚀边缘WC-KDSI 方法拥有更好的细节分辨能力,更能展现边缘的凹凸以及腐蚀中心的起伏情况;选择两处横向扫描位置(X1=250,X2=125)并采集一维轴向信号,得到如图7(d)中的A-scan信号分布,可见在不同横向扫描位置,WC-KDSI方法获得的重建图像相比传统KDSI 方法获得的重建图像,均具有更高的分辨率和信噪比;同时通过读取其PSF 的半高全宽,可以知道在探测深度100 μm 左右,使用WC-KDSI 方法可以分辨深度小于 4 μm 的镜面瑕疵.

图7 使用(a)直接FFT,(b)KDSI,(c)WC-KDSI 算法获得的镜面腐蚀微形貌OCT 重建图像;(d)不同扫描位置轴向PSF 比较Fig.7.Reconstructed OCT images of mirror corrosion by(a)direct FFT,(b)KDSI,(c)WC-KDSI method;(d)comparison of axial PSFs at different scanning points.

4.3 橘子果肉样本的成像实验结果

针对植物或生物等高散射组织,本文提出方法在三维图像高质量重建方面同样具有一定优势.选用橘子果肉样本,依次使用KDSI 方法及WC-KDSI方法进行相关处理,获得成像结果见图8.其中,图8(a)和图8(b)展示了KDSI 方法和WC-KDSI方法处理的果肉二维层析图像;由于系统光源谱段处于可见光波段,针对橘子果肉样本等高散射样本的穿透能力不足,因此获得的层析图像成像深度有限;但是,在果肉浅层深度,重建图像仍能较为清晰地分辨横向及纵向的果肉细胞壁组织,整体视野下WC-KDSI 方法拥有更高的对比度、分辨和细节分辨能力.图8(c)选取不同方法处理下、同一扫描位置的A-line 信号进行对比,在图中框选部分信号,相比于KDSI 算法处理结果(蓝色曲线),WC-KDSI 算法处理结果(红色信号)在多个果肉细胞壁位置均拥有更高的分辨率及信号强度,信号峰更突出,同时KDSI 处理信号的噪声普遍大于WC-KDSI 方法.综上,以上实验说明本文提出方法在高质量图像重建方面具有一定优势.

图8 使用(a)KDSI 算法及(b)WC-KDSI 算法处理获得的橘子果肉OCT 重建图像;(c)特定扫描位置的轴向PSF比较Fig.8.Reconstructed OCT images of orange pulp by(a)KD SI and(b)WC-KDSI algorithm;(c)comparison of axial PSFs at certain scanning position.

5 结论

在谱域OCT 系统中,光栅光谱仪的精确标定是快速傅里叶变换算法处理干涉光谱数据的前提,基于光谱域相位的光谱仪标定方法可以获得采样轴上的波数相对分布,因此被广泛采用.针对谱域干涉信号在采样边缘区域的信噪比不高、相位噪声较大的特点以及采样过程中的非线性特征,本文提出了基于特征谱线及约束拟合相位的光谱绝对波数标定方法,利用高信噪比区域的部分相位来拟合整个采样轴上的相位分布,结合特征谱线的特征相位值精确计算相位包裹次数,从而实现了采样轴上绝对相位的求解及绝对波数的精准标定.本文通过反射界面点扩散函数实验比较说明本文提出方法相比传统方法具有更高分辨率和更高信噪比,通过对比不同方法下两组量规离散界面的深度域采样位置和信号峰之间的采样间隔,说明了本文提出方法在离散界面精确定位方面具有优势;通过对反射镜镜面腐蚀微形貌、橘子果肉样本进行三维图像重建,详细分析轴向点扩散函数及层析图像信息,说明了本文提出方法可以实现更高质量的图像重建.