噪声标签识别与纠正的置信度预测方法

汪 敏,伍文静,刘瀚阳,闵 帆

(1.西南石油大学 电气信息学院,四川 成都 610500;2.西交利物浦大学 人工智能与先进计算学院,江苏 苏州 215123;3.西南石油大学 计算机科学学院,四川 成都 610500)

典型的弱监督场景包括不完全监督(incomplete supervision)、不确切监督(inexact supervision)和不准确监督(inaccurate supervision)[1],其中,噪声标签是最典型的一种不准确监督场景[2]。在使用传统的监督学习解决分类问题时,通常假设数据集样本都具有正确标签，然而,噪声标签在真实数据中无处不在。现实中,给数据标注标签的任务大部分是人为完成的,而数据信息量较少、标注人员本身的专业限制和个体间差异都会导致数据标注的结果不一致,从而很难获得标签全部正确的强监督信息。且噪声标签对模型性能的影响极大,不仅会使模型分类准确性严重下降,同时也会增加模型的复杂度。由于数据集规模巨大且类型复杂,通常无法人工逐一检查并纠正标签,因此,如何在弱监督状态下消除噪声标签对分类器模型的影响,是一项极具挑战的任务。

目前,噪声标签学习已逐渐成为弱监督学习领域的热点研究问题之一，针对这一问题,众多专家学者提出了许多解决方法[3]。这些方法一般分为对噪声容忍[4]和对噪声鲁棒性建模[5]两类。对固有噪声的容忍方法是最早被提出的噪声标签处理方法,发展初期,这类方法大多基于估计的噪声转移矩阵[6],以了解标签如何在不同类之间切换,构建满足统计一致性的学习算法,一般利用预先训练的模型和干净数据集直接计算估计转移矩阵[7-8],或间接使用联合优化技术、EM算法等计算转移矩阵中的元素[9-10]。但估算的噪声变换矩阵不一定准确,且不普遍适用,极有可能影响目标鲁棒分类器的性能。为减小噪声标签对分类器学习的影响,扩大适用范围,现阶段的研究通常围绕鲁棒性损失展开[11-12],其实质是通过添加正则项或修改网络概率等方式,使风险最小化,提高模型准确度,例如对损失函数的改进方法MAE、Lq和DualT等[13-14]。然而这类算法并不完全抗噪,且只在训练数据被少量噪声干扰时有效,表现出抗噪的不稳定性。

噪声鲁棒性建模主要包括噪声过滤和重加权。其中，最简单的方法是直接清理噪声数据[15],其基本思想是根据基分类器的预测结果进行噪声标签数据的识别,并删除该部分样本,代表算法包括过滤投票、SELF和CEROS[16-18]。但现有的算法大多认为噪声数据过滤方法易造成数据缺失,进而影响模型准确性,因此，更多地采用重加权策略对噪声数据进行研究。类似概率性局部离群因子算法(pLOF)[19-20],对样本相对重要程度进行新的定量分配[21-23],能够有效降低噪声样本对算法的影响。受人类“先易后难”的学习方式启发,稳定的CL学习框架[24]先学习干净标签,再学习噪声标签,解决了权重不易准确估计的问题。将CL思想融入噪声标签的学习中,相继出现了Mentornet网络、Co-teaching和Co-teaching+等[25-26]方法,明显增强了模型的鲁棒性。然而噪声鲁棒性建模的基础是一定量的干净数据,由于目前的数据标记场景复杂,很难对噪声分布做出合理假设,因此，在现有的实际场景中大多无法提供所需求的干净数据。

为了克服这些问题,本文提出了噪声标签识别与纠正的置信度预测方法(confidence prediction method for noise label identification and correction,CPRC),通过定义置信度推断方法,建立置信度连接,迭代实现置信度最优的噪声标签识别与纠正。首先,将数据样本按置信度与距离的不同分类,在样本分类的基础上,定义初始可信样本选择策略,筛选优质的可信样本,建立样本间置信度动态预测的基础。其次,根据数据间固有的分布特性,分析样本标签误差与距离之间的联系,建立样本之间的置信度连接,设计两种基于样本关联度的标签概率预测方法,推断样本标签置信度。最后,迭代搜索最优置信度样本,优化更新样本预测标签,结合阈值与预测标签进行样本处理,识别并纠正噪声标签。

1 问题定义

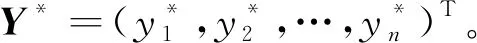
在获得Y*的过程中，引入如下几个概念。给定置信度阈值β1，E={xi|b(xi)≥β1}为高置信度样本集合，这里b(xi)除与置信度阈值有关，还受标签变化影响；E′⊆E，为可信样本集合，其元素还需要满足标签一致性条件；R=XE′为不可信样本集。为准确识别与纠正噪声标签，对不可信样本进行迭代搜索，每一轮迭代只选择一个置信度最高的优质样本，即

(1)

其中：λ是邻域半径；δ(E,R,λ)为E在R中的λ邻域。在每次获得最大置信度样本的搜索过程中，考虑样本间的可信关系约束。

2 噪声识别与纠正算法 CPRC

2.1 算法框架

在本文的方法中，主要分为初始可信样本筛选、样本标签置信度预测和噪声标签识别与纠正3个模块。首先，定义初始可信样本选择策略，筛选优质的可信样本；然后，通过标签概率预测方法推断样本标签置信度；最后，迭代搜索不可信样本中的最高置信度样本，利用置信度阈值识别噪声样本，通过softmax标签预测，实现噪声标签纠正。CPRC算法框架如图1所示。

图1 CPRC算法框架

2.2 初始可信样本筛选

由于噪声的随机性，通常不存在绝对干净的样本。为获得可信度较高的近似干净的样本，本文通过对样本数量与标签比例的假设，筛选符合条件的可信样本。

首先，构建样本xi以λ为半径的邻域Hλ(xi)={xj∈X{xi}∣d(xi,xj)≤λ}，根据样本之间存在的置信度b(xi)与距离d(xi,xj)的差异，将邻域内的样本进行详细分类。

对置信度b(xi)而言，若b(xi)≥β1，xi∈E为高置信度样本；若b(xi)<β1，xi∈XE为低置信度样本。则邻域Hλ(xi)可细分为高置信度邻域HE(xi)={xj∈X{xi}∣xj∈E∩Hλ(xi)}与低置信度邻域HU(xi)={xj∈X{xi}∣xj∈Hλ(xi)HE(xi)}。若进一步考虑可信样本集，在高置信度邻域内又有可信邻域HE′(xi)={xj∈X{xi}∣xj∈E′∩Hλ(xi)}。

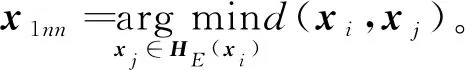
其次，聚集邻域Hλ(xi)内与xi标签相同的样本xj，记标签yj=l，将符合条件的样本簇表示为

Cl(xi)={xj∈Hλ(xi)∪xi∣yj=l}。

(2)

计算标签l在邻域内所有样本标签中所占的比例，

(3)

最后，设置样本筛选阈值α1和α2，当邻域Hλ(xi)内的样本总数不小于α1，且与xi标签相同的样本所占比例M(xi)大于α2时，则认为样本xi为初始可信样本，其标签完全可信，设其置信度b(xi)=1，并加入可信样本集E′。

图2B～2D举例说明了初始可信样本筛选的不同情况。假设阈值α1=8，α2=1/2，在半径为λ的邻域中，图2B关于x10的邻域内共有9个样本，|Hλ(x10) |+1=10>α1，其中，x10与x5、x6、x7、x9标签相同，且该类标签数量最多，|Cl(x10) |=5，此时M(x10)=1/2≥α2，满足条件，认为x10是初始可信样本，令其置信度b(x10)=1；图2C关于x1的邻域内共有7个样本，|Hλ(x1) |+1=8≥α1，其中，x1与x2、x3的标签相同，且该类标签数量最多，|Cl(x1) |=3，但M(x1)=3/8<α2，不满足条件；图2D中，关于x6的邻域内共有6个样本，则|Hλ(x6)|+1=7<α1，不满足条件。

图2 初始可信样本筛选

2.3 标签置信度预测

本文噪声标签识别与纠正方法CPRC基于置信度的预测，对于任意样本xi∈X，CPRC建立样本之间的连接关系，推理计算各个样本的置信度。

2.3.1 样本关联度计算 通常认为，样本之间越接近，标签不一致的概率就越低。利用数据之间这种固有的分布特性，本文使用标签不一致统计方法[27]，分析样本标签误差与样本间距离的关系，得到样本对之间的标签不一致概率，表示样本间的连接关系。

首先，考虑所有样本以λp为半径的邻域，根据式(4)计算邻域内样本对(xi,xj)的标签不一致误差p(λp)，

(4)

其中，Hλp={(xi,xj)∈X×X∣d(xi,xj)≤λp}是相对于邻域半径λp的相邻样本对。

图3详细展示了标签关联度及样本置信度计算的不同情况。考虑邻域半径λp=0.3，则有(x1,x5)、(x2,x3)、(x2,x6)共3组样本对的样本间距离小于等于λp。其中，(x2,x6)具有不同标签，则p(λp)=1/3；取λp=0.58，则有(x1,x5)、(x1,x6)、(x2,x3)、(x2,x4)、(x2,x6)、(x3,x4)、(x3,x6)、(x4,x5)、(x4,x6)、(x5,x6)共10组样本对的样本间距离小于λp，其中，仅(x1,x5)、(x2,x3)、(x4,x6)共3组样本对具有相同标签，则p(λp)=7/10。

然后，拟合标签不一致曲线φ(λp)。本文经验性地选择了30个不同大小、类别、维度和形状的数据集对标签不一致误差p(λp)进行统计，获得统计函数的估计值进行拟合，得到实际的标签不一致统计函数，

φ(λp)=(804.3λ-1.381)/(λ3+1 621λ2+286.2λ+1 221)。

(5)

最后，根据样本间的距离λp，查询φ(λp)，得到样本间标签不一致的概率，表示为样本间的连接关系，即样本关联度

a(xi,xj)=1-φ(d(xi,xj))。

(6)

2.3.2 样本置信度计算 定义样本间的连接关系，获得样本关联度后，通过两种基于样本关联度的标签概率预测方法，推断样本标签置信度b(xi)。

若样本xi的邻域内只有一个高置信度样本xj，通常采用单实例置信度推断方法。此时，xi相对于xj的单实例置信度为

bs(xi,xj)=b(xj)a(xi,xj)。

(7)

图3B～3C举例说明了单实例置信度的计算步骤。对于待预测样本x1，首先通过邻域半径λp查询x1与高置信度样本x3的标签不一致概率φ(λp)，通过样本关联度a(x1,x3)，利用式(7)计算样本x1的置信度bs(x1,x3)。

若样本xi的邻域内有多个高置信度样本，则使用邻域置信度推理方法。此时，xi的邻域置信度为

bo(xi,HE(xi))=bs(xi,xj)+

(1-bs(xi,xj))×

(8)

其中：bs(xi,xj)是最近高置信度邻居xj(xj=x1nn(xi))的置信度；xl是邻域内除xj外的其他高置信度样本。

通常认为，样本间越接近，样本标签相同的概率越大；邻域内相同标签的样本数量越多，待预测样本标签越趋同。因此，在邻域置信推理方法中加入指示函数I(yl)，

(9)

当xl与xj的标签相同时，取I=1，否则为I=-1，以此增大不同标签样本间的置信度差异。

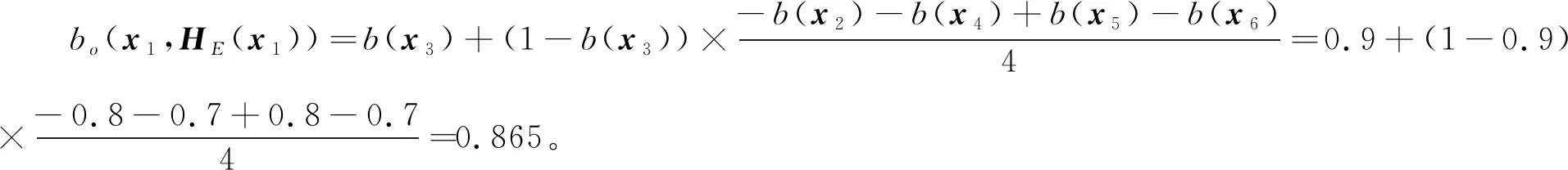
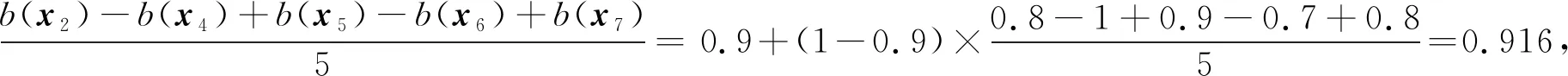
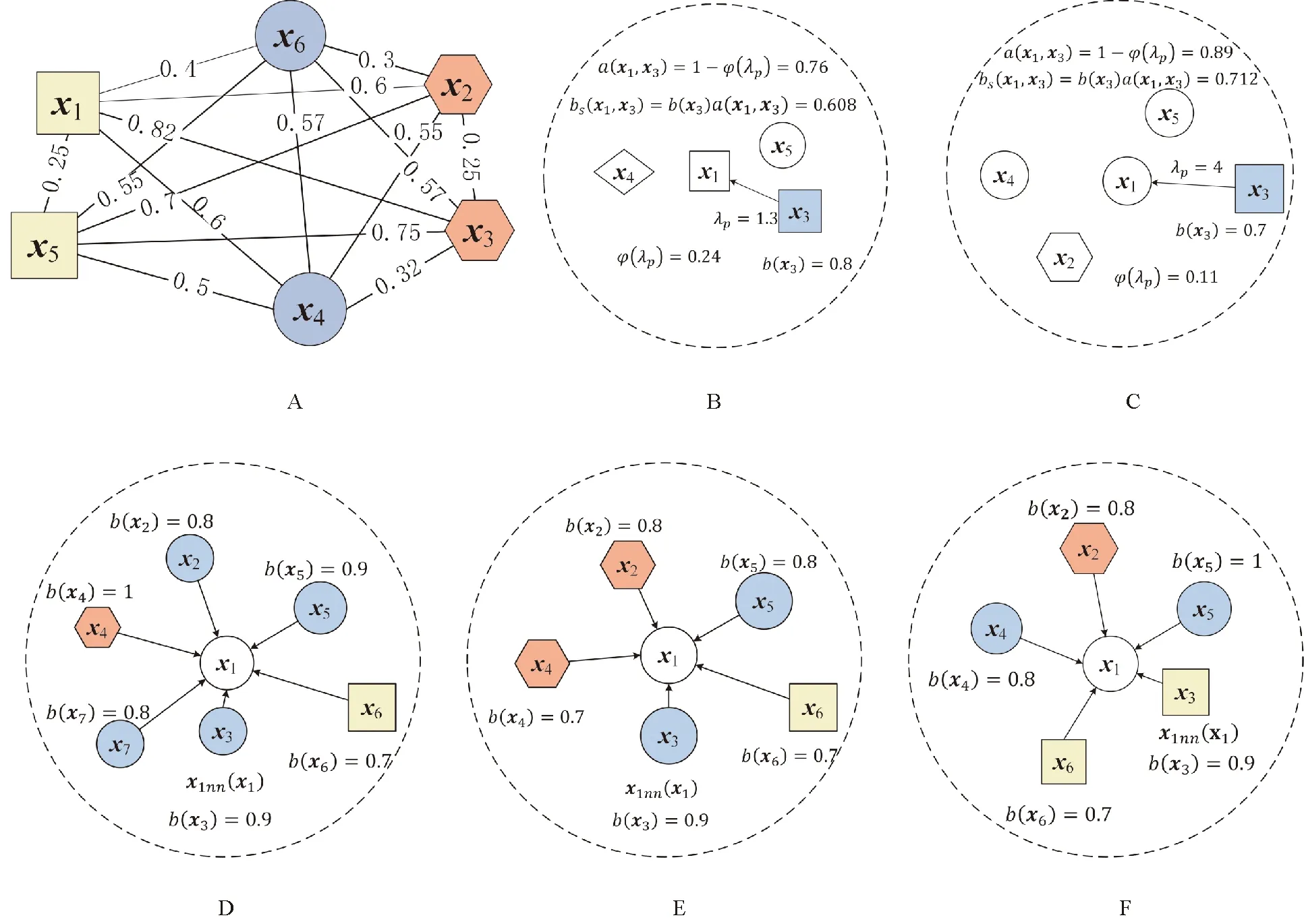
图3 样本置信度预测

2.4 标签识别与纠正

基于初始可信样本的筛选与样本置信度的计算，通过迭代搜索不可信样本集R=XE′中的最高置信度样本，结合置信度阈值和对样本的标签预测，识别并纠正噪声样本，具体步骤如下。

第1步：在δ(E,R,λ)={xi∈R|d(xi,xj)<λ，xj∈E}内，搜索一个拥有最高置信度的优质不可信样本

xt=arg maxx∈δ(E,R,λ)b(x)。

(10)

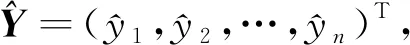
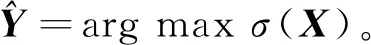
(11)

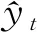
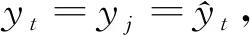
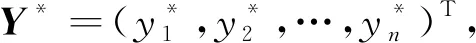
2.5 伪代码

算法1给出了CPRC的完整步骤，包括初始可信样本筛选、样本标签置信度预测、噪声标签识别与纠正3个部分。第1～2行通过约束条件选择高质量的初始可信样本；第3～6行通过样本间标签与距离的差异，计算样本置信度；第7～20行搜索拥有最大置信度的不可信样本xt，根据被查询样本xt与其最近高置信度邻居xj的标签一致性，使用softmax预测结果纠正xt的标签。最后采用任意监督算法对样本进行分类。

算法1噪声标签识别与纠正的置信度预测方法(CPRC)

输入 含错误标签的训练集D，样本筛选阈值α1、α2，置信度阈值β1、β2

输出 分类标签L

1)利用样本筛选阈值α1、α2获得初始可信样本集E′；

2)E←E∪E′；

∥步骤1筛选初始可信样本

3)根据式(5)查询标签不一致概率φ(λp)；

4)根据式(6)计算样本关联度a；

5)fori←1 to |R| do

6) 根据式(7)和(8)得到样本置信度b(xi)；

∥步骤2计算样本置信度

7) 根据式(10)搜索最高置信度样本xt；

8) fori←1 to |E′|do

10) end for

11) ifb(xt)>β1then

12) 更新高置信度样本集E←E∪xt；

14) 更新可信样本集E′←E′∪xt；

15) end if

16) end if

17) ifb(xt)>β2且yt≠yjthen

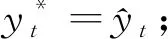
19) end if

20) end for

∥步骤3识别并纠正标签

21)L←Supervisedclassify (D)。

3 实验与分析

3.1 实验设置及评价指标

为验证本文所提CPRC算法的有效性，选取了6组多分类测试数据集进行实验,包括Aggregation、DLA0.01、Seeds、Page-blocks、Penbase和Balance-scale。详细的数据集信息如表1所示。

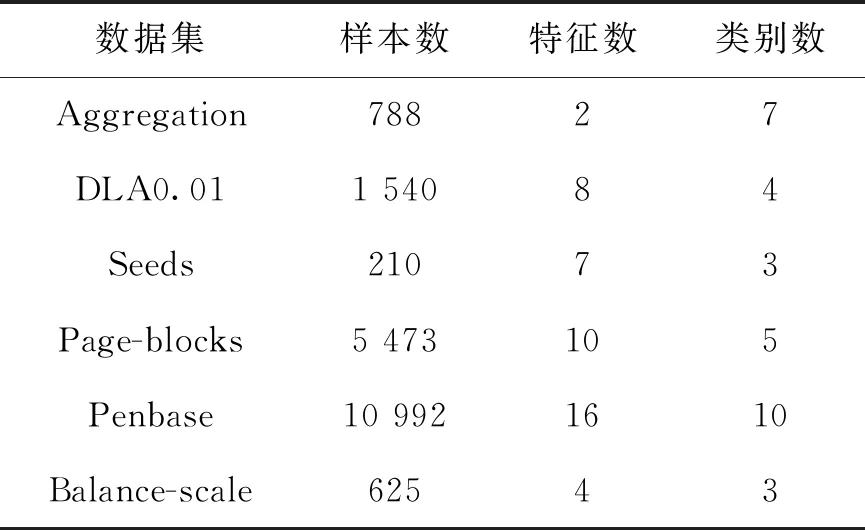
表1 本文使用的多分类数据集

由于样本标签的准确性对监督学习的分类性能有显著影响,故本文采用样本分类准确率,即预测精度Acc作为评价指标，

(12)

其中：n是数据集总样本数,e是错误分类的样本数量。

对于每个数据集,选取40%进行训练,60%用于测试。为了保证实验的准确性,在每个数据集上,随机化重复10次实验,计算平均分类准确率和方差并进行分类性能统计分析。为获得最优实验结果,根据经验,将CPRC方法的样本筛选阈值设置为α1=8，α2=0.8，置信度阈值设置为β1=0.95，β2=0.5。

3.2 实验结果与对比分析

为了验证CPRC是否能够有效提升监督分类算法的精度,本文实验将1NN、3NN、Tree和Bagging 4种经典的监督分类器作为基分类器,其中,1NN和3NN是两种最常用的最近邻分类算法;对于Tree,本文采用分类回归树CART;Bagging结合了多种弱分类算法,能有效降低泛化误差。设置20%的噪声率,在4种基分类器上应用CPRC算法,分别在6个数据集上进行分类实验,表2和表3给出了其与不使用任何噪声处理算法的分类对比结果,对分类性能最好的结果进行加粗显示。“CPRC-”表示采用CPRC进行标签纠正降噪后，再使用分类器进行分类。

表2列出了1NN、3NN在6个数据集上的分类准确率,以及在1NN、3NN上应用CPRC进行标签纠正降噪后的分类准确率。使用CPRC算法的分类器与不采取任何降噪措施的分类器相比,在所有6个数据集上的分类准确率都有3%左右的精度提升。例如,在Aggregation数据集上,1NN的分类准确率为79.53%,CPRC-1NN的分类准确率为86.27%,精度提升了8%左右。在Pageblocks数据集上,CPRC-1NN的分类准确率为85.89%,远高于1NN (76.41%)。

由表3的结果可知,在Tree和Bagging分类器上应用CPRC算法后,在6个数据集上的实验结果相比于未使用CPRC算法的基分类器均有不同程度的提升。由于Bagging对噪声不敏感,Page-blocks和Penbase数据集在CPRC-Bagging上的分类准确率分别为94.82%和97.78%,虽然略低于在Bagging上的分类准确率(94.83%和98.01%),但仅相差0.01%～0.23%,且在其他数据集上,CPRC仍然能够进行噪声标签的有效识别与纠正。

根据表2和表3的实验结果,本文提出的CPRC算法在6个数据集上整体表现优异,显著提高了经典监督分类器的分类性能,可有效提升监督分类算法的精度。

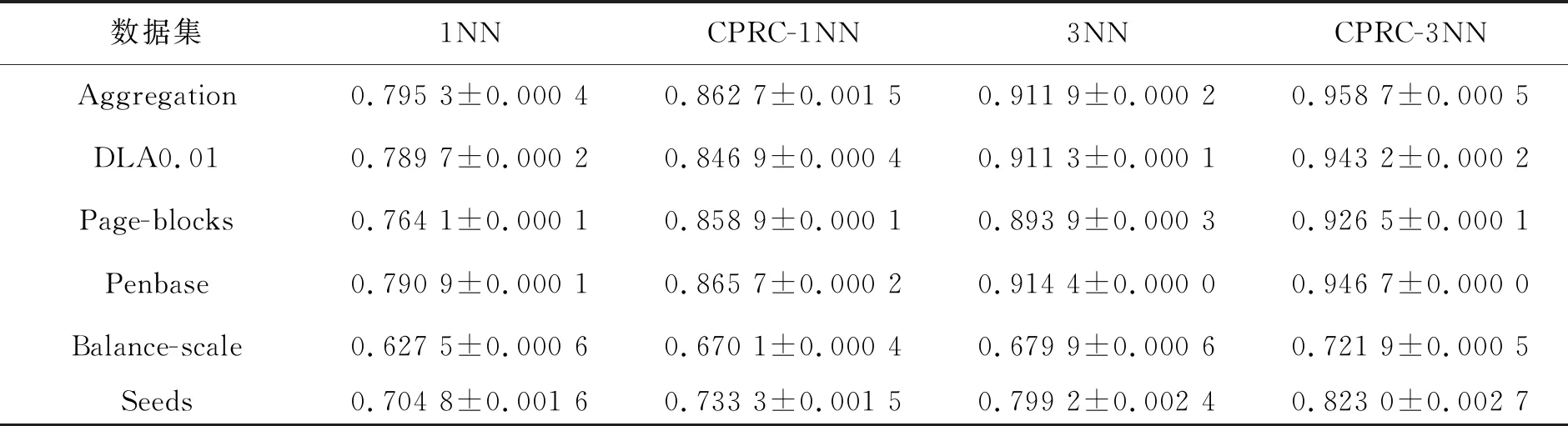
表2 CPRC在1NN和3NN上的分类准确率

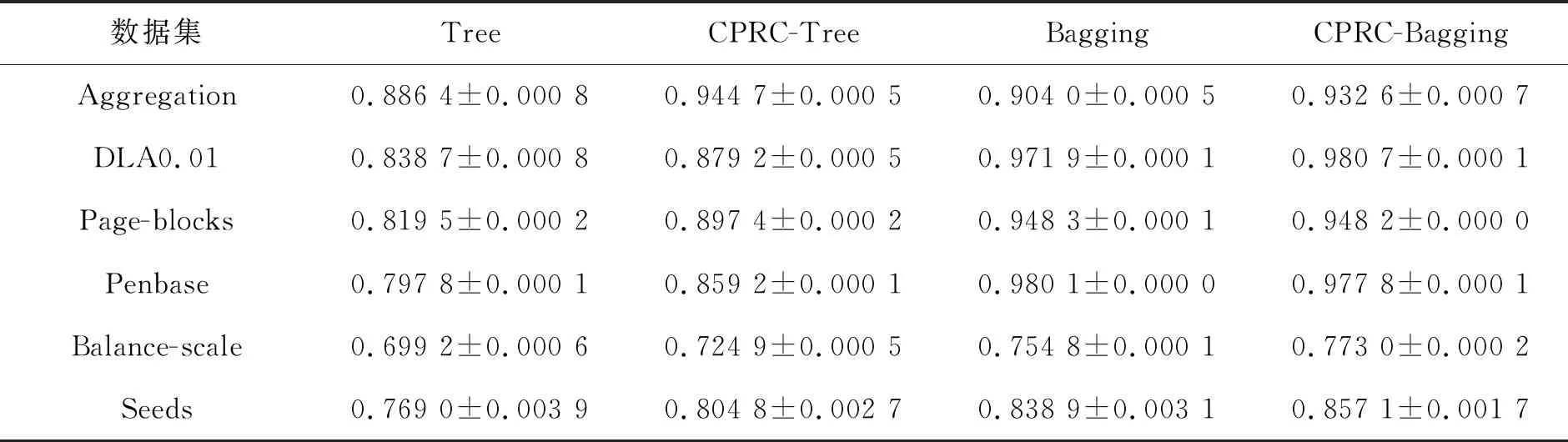
表3 CPRC在Tree和Bagging上的分类准确率

图4进一步展示了在不同噪声环境下CPRC算法的性能。考虑噪声率分别为10%，15%，20%，25%，30%,4种监督分类器在不同噪声率下都实现了性能的显著提升。例如,对于Aggregation数据集,在30%的噪声率下,3NN和CPRC-3NN的准确率分别为83.24%和91.84%。对于Balance-scale数据集,受15%的噪声率影响,1NN和CPRC-1NN的准确率分别为65.61%和70.35%。在25%的噪声率下,数据集DLA0.01的分类准确率由Tree的78.72%提升到CPRC-Tree的86.89%。

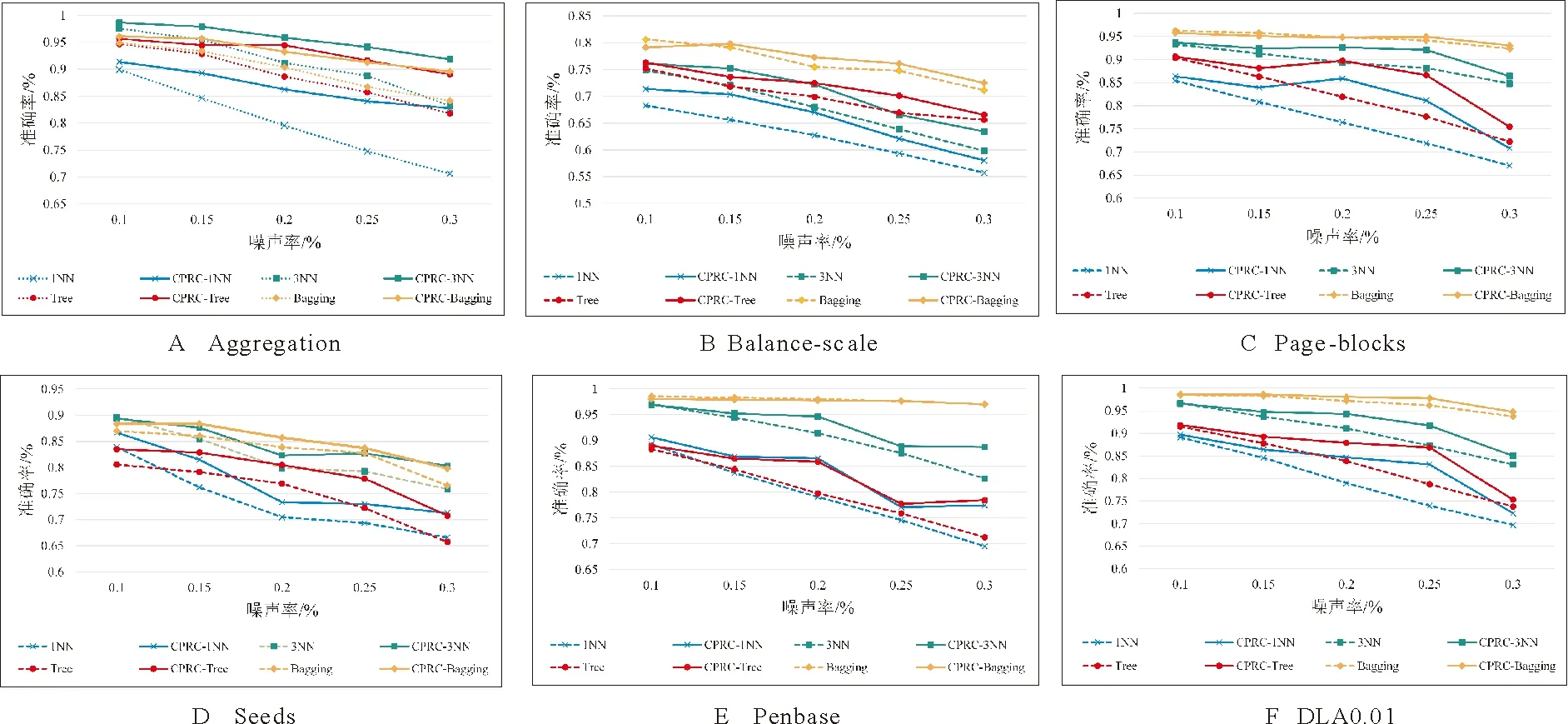
图4 不同噪声环境下4种监督分类器在应用CPRC算法后的性能对比

实验结果表明,本文提出的CPRC算法在不同的噪声环境下均能有效识别并纠正噪声,降低了噪声标签对模型分类性能的影响,具有良好的鲁棒性。

为进一步验证CPRC算法的优越性能,将CPRC-3NN、CPRC-Bagging与DPNLD[28]、LNPCC[29]两种先进的噪声标签学习算法进行比较。其中,DPNLD是基于密度峰值的高光谱图像噪声标签检测算法，LNPCC主要讨论标签噪声下半监督学习中的粒子竞争与合作。实验中采用的源码及配置信息严格引用原文以确保最佳性能，实验结果如图5所示。

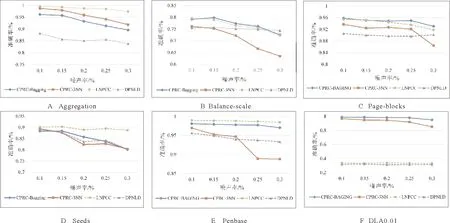
图5 CPRC与DPNLD、LNPCC的性能对比

从图5可以看出,在不同的噪声率下(10%，15%， 20%， 25%， 30%), 相比于DPNLD和LNPCC,CPRC算法具有稳定的标签识别与纠正能力,鲁棒性更好。相较于LNPCC,在Aggregation、Seeds数据集上应用CPRC算法,其分类精度并不理想,但比DPNLD更具优势,且有效提升了基分类器的效果。而在Page-blocks、Balance-scale、DLA0.01上,CPRC算法相较于DPNLD和LPNCC均有不同程度的性能提升。例如,在Page-blocks上,加入25%的噪声,DPNLD和LPNCC算法下的分类精度分别为89.62%和93.51%,CPRC-Bagging则表现出94.97%的准确率。特别地,对于数据集DLA0.01,由于特征之间高度相关,特征变量冗余,导致算法LNPCC与DPNLD不收敛,标签识别与纠正能力降低,但CPRC依然有优异的表现。

综上,从标签识别与纠正的角度考虑,与几种目前先进的噪声标签学习算法相比,CPRC综合表现更佳,具有较强的鲁棒性;从模型分类性能的角度考虑,在不同噪声比下,CPRC均能有效识别并纠正噪声标签,在不同类型基础分类器上的分类性能都更优越。

其次,本文使用的初始可信样本筛选策略建立在对样本数量与标签比例的假设基础上,所选择的初始可信样本需满足“邻域内样本总数不小于α1，且与其标签相同的样本所占比例大于α2”的条件。基于实验中所设置的参数α1=8，α2=0.8，对于数据集Penbase，至多挑选出67个初始可信样本，占所有干净样本总数的2.7%；对于数据集Balance-scale，挑选出的初始可信样本数量仅在干净样本总数的8%～12%之间，均无法筛选出大规模可信样本。未来需要进一步考虑初始可信样本选择的理论模型和理论证明。

4 结语

为降低噪声标签对模型分类性能的影响,本文提出了一种噪声标签识别与纠正的置信度预测方法(CPRC),通过定义置信度推断方法,建立置信度连接,迭代搜索最高置信度样本进行噪声标签识别与纠正。对不同类型基础分类器在不同噪声比下进行了实验,表明CPRC对初始可信样本的筛选有效,考虑样本间标签误差与距离的置信度计算方法准确,使用阈值与预测标签进行标签识别与纠正的处理方式合理。

未来的研究工作主要包括以下两个部分:

1)减少标签识别与纠正过程中的阈值使用,进一步优化噪声标签识别的敏感程度与噪声标签纠正的准确率;

2)改进初始可信样本的筛选策略,加强初始可信样本的信任程度,降低错误筛选的样本对标签识别与纠正的负面影响。