激光衰荡测量中腔内能量动态过程分析研究

朱 媛,余 锦,貊泽强,唐吉龙,魏志鹏

(1.长春理工大学高功率半导体激光国家重点实验室,吉林 长春 130022;2.中国科学院空天信息创新研究院,北京 100094； 3.中国科学院计算光学成像技术重点实验室,北京 100094;4.中国科学院大学,北京 100094)

1 引 言

腔衰荡光谱检测(Cavity Ringing-Down Spectroscopy,CRDS)是一种以无源腔腔内能量变化为测量对象的增强吸收光谱技术,通过分析测量出射光的衰荡时间来表征腔内物质特性,具有高分辨率、高灵敏度和超长光程的检测特点,在大气环境监测[1-2]、医学实验研究[3-5]和社会安全保障[6-7]等领域得到广泛的应用。通常,CRDS装置的检测精度是通过衰荡时间测量准确度来进行表征[8]。

对连续波腔衰荡光谱检测,腔衰荡事件产生的前提条件是实现良好的纵模匹配,即入射激光波长与腔衰荡某一本征振荡模式之间实现匹配。目前,基于频率匹配的理论有两种:多光束干涉理论和基于Q值能量守恒理论。1984年,D.Z.Anderson等[9]基于多光束干涉理论,利用腔的传递函数对腔衰减法的测量原理进行了严格推导,并根据推导结果分析和讨论了腔衰荡法的适用条件,为理解和掌握该技术特点提供了参考,其他研究人员也对该推导过程进行重新阐述和数值仿真[10-11]。2007年,谭中奇等[12]基于能量守恒原理及无源腔Q值定义式,从新角度对连续波腔衰荡技术的测量原理进行了推导,模拟了入射光关断时间以及无源腔充光效率等因素对测量结果可能造成的影响。这种推导方式相对于传统多光束干涉理论的推导方式而言,其物理含义更为明显,推导过程更为简单。针对连续波腔衰荡测量中衰荡线形畸变及其对检测精度的影响等问题,该方法能够进行数值模拟和分析,有助于系统精度的提高。但该方法没有考虑入射光频率不满足谐振条件下的情况,在使用模拟时存在一定误差。

实验上,一般采用腔长扫描[13-15]和波长调制[16]两种途径来实现纵模匹配。腔长扫描是指保持入射激光波长固定,通过位移器件(如压电陶瓷)驱动腔镜做往返运动,进而引发腔长的周期变化来实现频率匹配；波长调制是指衰荡腔长不变,通过调制激光波长实现激光和衰荡腔的频率匹配,波长调制不需要额外的电压调制器和位移器件等,从而大幅简化了衰荡结构,因而在低成本器件上有着更大的优势,在球载[17]等工程上也具有相关应用前景。Paldus等[18]首次提出电流调制频率匹配技术,通过完全关断激光驱动实现注入激光的关断,最小可探测灵敏度为1×10-9cm-1。国内的赵刚等[19]也对波长调制方法进一步改进,通过二次谐波检测实现无校准波长调制,检测精度提升了4倍。

本文考察了电流调制的连续波激光衰荡过程,基于衰荡腔内外能量守恒原理,对充光过程中频率匹配、关断过程中线性畸变及衰荡过程中输出衰减进行了数值模拟,建立了腔衰荡全周期腔内能量动态模型。实验通过触发阈值调节和关断时间延迟,验证了充光时间对检测精度提高的有效性。

2 仿真模拟

2.1 理论基础

在无源谐振器中通常使用品质因数Q值来标志腔的特性,衰荡腔作为一种无源谐振器,可通过Q值将衰荡时间和能内能量联系起来[20],从而表示衰荡腔内能量的变化过程。图1为无源腔内能量转换图。

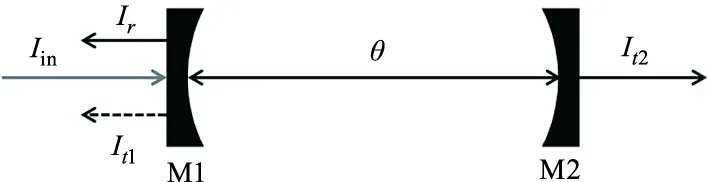
图1 无源腔内能量转换图Fig.1 Energy conversion diagram in passive cavity

根据Q值能量守恒定律,腔内能量转换过程可表示为:

(1)

(2)

其中,Iin为外部入射光腔；Ir为M1处的反射光；θ为腔内能量；It2为M2处的透射光;Iin为没有频率匹配反射的光强;t0为无外部入射光时因腔透射损耗而产生的时间常量。当入射光能量大于腔镜透射出的能量时,腔内能量开始积累,腔内总能量的变化可用方程表示为:

(3)

其中,τR为衰荡腔的衰荡时间,结合式(1)～(3)可推导腔内光起振的过程,腔内能量公式如下:

(4)

2.2 充光过程

由公式(4)可知,在腔镜确定后,衰荡时间及入射光强决定腔内能量的变化过程。空腔时的衰荡时间由腔镜和腔长确定,因此必须明确纵模匹配后的入射光强。在波长调制中,保持光学谐振腔长度不变,激光频率在一定时间范围内快速扫描,经过匹配后的入射光强可表示为:

(5)

其中,*表示卷积运算;FWHM为激光线宽;υ为激光扫描速度;F为衰荡腔精细度;Δν为腔的纵模间隔;C为常数。

我们对衰荡腔长为340 mm、腔镜反射率为99.99 %的波长调制的CRDS装置[21]进行数值模拟。计算得到,此时衰荡腔腔模半高宽约为14 kHz,腔自由光谱范围441 MHz。假定线宽为1 MHz的入射激光初始中心频率与衰荡腔共振频率完全失谐,并且激光中心频率扫描速度为100 kHz/μs,频率扫描范围包含一个自由光谱范围。在模拟计算时,为了简化计算将腔模近似为长为腔模半高宽、高为1的矩形,激光模式近似为高为1的高斯线形。

入射激光的频率扫描过程如图2所示,图中I0(v)表示激光频率,CT(v)则代表谐振腔模频率。计算式,假定衰荡腔模式频率保持不变,激光中心频率从偏差+1500 kHz处向完全匹配处扫描。

(a)

图2(a)为扫描过程中激光频率中心和纵模中心存在较大偏差,二者交叠但没有重合的情况,此时的充光速率较低；(b)为二者完全重合的情况,此时充光速率达到最大。

图2中,对于入射激光频率扫描过程,可以认为充光过程某一时刻代表激光光束的高斯线型与代表腔模式的矩形之间相互交叠区域的面积,对应该时刻能量注入速率,定义K来表示能量的变化速率,则K可表示为:

((ν-υ0t)/δ)2)

(6)

其中,ν为激光中心频率；υ0为激光中心频率速度；δ为激光频率模型标准差。该时刻衰荡腔内部光强为充光能量注入速率K对时间的积分,即有:

(7)

作为对比,我们也画出按照文献使用e指数充光模型[21]来表示腔内充光光强Iin1的增长趋势:

Iin1=I0(1-exp(-t/ts))

(8)

其中,I0为初始光强,ts为激光关断时间。图3(a)为两种充光模型的光强对比,图中可以看出,e指数充光模型比激光扫描模型充光速度更快,在50 μs处就率先达到充光归一化状态。图3(b)为两种模型的能量注入速率,e指数模型注入速率在零时刻最大,之后快速衰减；波长调制的充光速率呈高斯线型增长,在50 μs处注入速率最高。可以认为,由于e指数模型完全忽略了入射激光与衰荡腔模式的匹配与失配对能量注入、储存的影响,所以该模型给出的是最理想情况,即连续波衰荡测量中纵模始终保持匹配的情况。在波长调制、腔长调制等频率匹配过程中不可能出现这种始终匹配的条件,因此,扫描充光光强模型相较于e指数模型更具有适用性。

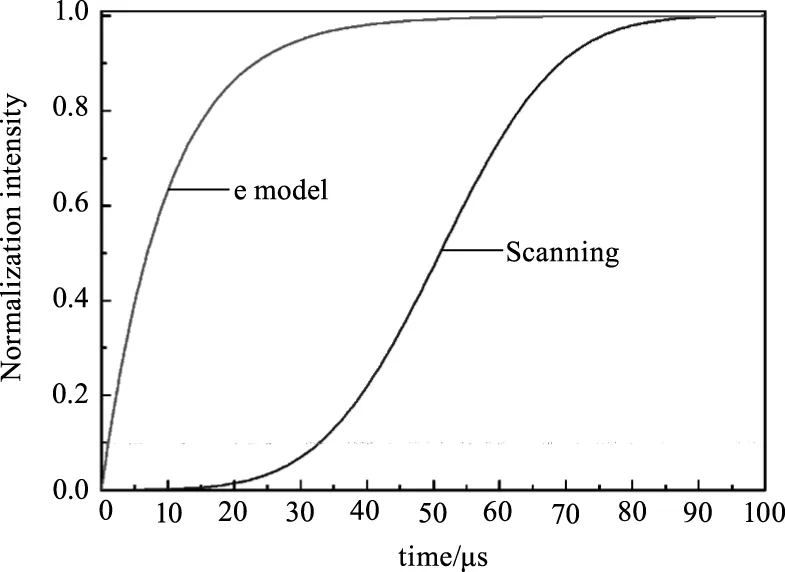
(a)两种光强模型

2.3 关断过程

关断过程是指当光电探测器接收到的透射光强达到设定阈值时,控制单元发出关断指令,关断入射光注入。理论上,关断阈值的设定应为满充光状态下的透射光强,但实际情况下由于外界干扰,激光频率和腔纵模频率难以长时间维持匹配状态,透射光强将会远低于满充光状态。

理想状态下关断在瞬间完成,用阶跃函数表示,衰荡过程如图4(a)所示。图中可以看出,无论充光程度多少,衰荡都是e指数衰荡线型。实验中使用光电器件关断,关断时间存在导致衰荡线型会产生非e指数衰荡的线型畸变现象,这种现象在其他文献中也有出现[22],被定义为过充现象。图4(b)为存在关断时间的衰荡曲线,对比可以看出,在充光时间为11 μs时,衰荡开始的初期存在上升屋脊；在满充光状态下,并不存在该现象。因此,衰荡线型的过充现象,是因为在关断时间中的注入速率不为零,存在充光能量大于腔内损耗的能量,导致短暂的总能量上升状态；在探测器上表现为当透射光强达到触发阈值后,透射光强先增加后再衰减。图中充光到满状态所需时间为30 μs,充光到0.12的充光时间仅为11 μs；前者光腔衰荡全过程周期至少为60 μs,后者的光腔衰荡全过程周期为41 μs,即后者测量频率是前者的1.5倍。理论上,CRDS测量的空腔衰荡时间与充光程度无关,可通过缩短充光时间提高测量频率。而测量中,由于存在噪声影响[23],充光程度较低会引起衰荡信号幅值的降低,进而导致测量信噪比及检测精度的降低。因此可通过设置合适的充光时间达到测量频率及精度的统一。

(a)

实验中采取电流调制方法时,失谐关断产生的延迟无法忽略。延迟时间为关断电信号从产生到实现关断功能单元所需的时间,假定延迟时间为1 μs,此时间内充光光强呈线性增长,则增长斜率为充光光强在关断时的注入速率,在该过程中,充光光强增加,腔内能量持续注入,属于充光过程,光强公式可定义为Id=I1+K·td,Id为关断延迟时间内的光强,I1为充光结束时的光强大小,td为关断延迟时间；而关断时间相对较短,假定为0.1 μs,在关断时间中,充光光强不会继续增加,属于衰荡过程,此时光强可采用e指数公式Ird=I0exp(-t/ts)表示。

2.4 衰荡过程

在模拟中,通过对不同充光时间的衰荡过程进行模拟,得到衰荡曲线图5。从图5(a)中可以看出,当充光时间为25 μs时,衰荡开始时的腔内能量仅占完全充光能量的60 %,开始即为充光不足状态；当充光时间为30 μs时,腔内能量完全充光并且在衰荡初期存在明显屋脊的过充现象。充光时间决定了衰荡开始时的初始腔内能量,但无论充光是否充分,关断时间内的能量增量使得腔内总能量上升。图5(b)为充光时间30 μs时的衰荡曲线及其拟合曲线,拟合曲线呈单e指数,拟合优度较高(R2=99.82 %)。从图5(b)残差图可以看出,衰荡信号仅在衰荡初期与单指数形式有所偏离,可能是关断时间内的线型畸变导致。

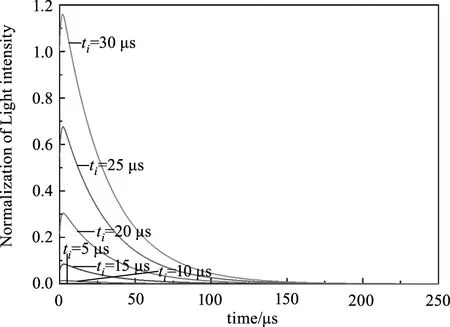
(a)不同充光时间下的衰荡能量图

2.5 全周期过程

通过对充光过程、关断过程进行分析,再结合衰荡过程可以描绘出光腔衰荡测量全周期光强变化过程:入射光进入衰荡腔实现有效充光,其表现为透射光强逐渐增大,充光时间为t1；当透射光强达到触发阈值时,主动关断,关断延迟的时间为t2;在弛豫时间影响下,衰荡曲线偏离单e指数的理想衰荡曲线；全过程光强公式表示如下:

ε(t-t1)+(I1+K·td)·ε(t-t1)ε(t2-t)+

I0exp(-t/ts)·ε(t-t2)

(9)

其中,ε(t)为单位阶跃函数。光腔衰荡全周期过程是一个完整的测量时间,也是CW-CRDS气体检测能实现的最短采样周期。

图6(a)为充光时间为20 μs、25 μs和30 μs下的充光能量全过程图,可以清楚看到全周期过程分为三个阶段,充光阶段、关断阶段和衰荡阶段。对不同充光时间下的过充大小进行研究,图6(b)中“θ”线为充光时间从0～30 μs的过充数值,“Δθ/θ”曲线为过充能量与腔内总能量的比值。随着充光时间的增加,过充能量增加的趋势与注入光强基本一致,占腔内能量比值先增大再减小,在注入速率最快时,过充能量达到最大；在充光完全时,衰荡过程中过充值对腔内总能量的影响降低仅占当前腔内能量的15 %左右。

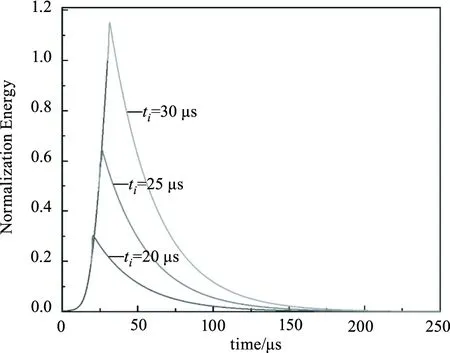
(a)不同充光时间下的全衰荡能量过程图

2.6 噪声模拟

CRDS实验装置的测量灵敏度可以用噪声等效吸收系数αeq的最小值αmin来表示[24]:

(9)

其中,c为光速；Δτ为衰荡时间τ的标准偏差。由式(9)可知,Δτ/τ的值直接影响噪声等效吸收系数,进而影响测量灵敏度,所以在腔长和腔镜反射率固定时,提高衰荡时间的测量精度(Δτ/τ)是提高测量灵敏度的有效途径。

实验中产生的噪声是无法完全避免的,也是限制CRDS精度进一步提高的主要因素。在模拟测量精度方面,使用衰荡时间的标准偏差与平均值的比值(Δτ/τ)来表示。对不同充光时间模拟衰荡曲线添加高斯噪声,并对其衰荡曲线进行拟合,结果如表1所示。表中可以看出,随着充光时间的增长,由于关断时间过充数值影响,拟合衰荡时间τ从32.24 μs降低至31.01 μs,但衰荡标准差从0.0434 μs降低至0.0036 μs,Δτ/τ从1.35减少至0.012,检测精度提升10倍左右,曲线的拟合优度也随之提高。

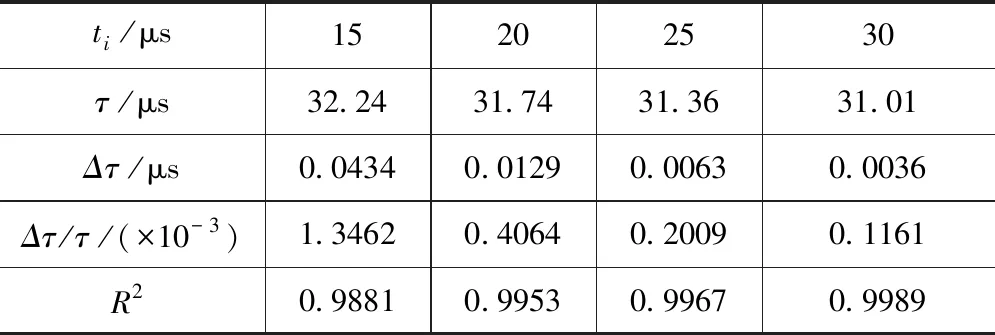
表1 不同充光时间模拟衰荡曲线的拟合Tab.1 Fitting of simulated ring-down curves at different light filling times

3 实验及结果讨论

CRDS检测装置光路示意图如图7所示。采用光纤耦合输出的DFB激光器为光源,中心波长为1653.7 nm,激光器控制器的电流设定为130 mA,工作温度为20 ℃。利用信号发生器加载一个三角波调制信号,调制频率为20 Hz,幅值为26 mV。激光经准直器、模式匹配镜后,耦合进衰荡腔。由于衰荡腔采用直线腔,所以在光路中加入光隔离器来抑制其产生的光反馈。准直后的激光经横模匹配耦合进衰荡腔,透射光聚焦在探测器接收面上,由示波器进行采集。当达到触发阈值时,示波器向控制器发出关断信号,通过工作电流在小范围内变化(不关断工作电流)改变激光频率,实现失谐关断。通过示波器监测衰荡事件,显示并记录衰荡曲线。实验过程中,采用质量流量控制器,以0.5 L/min的速率向衰荡腔中持续通入氮气。为减小水汽及空气颗粒对实验结果的影响,在衰荡腔输入输出气路上,均装有干燥剂和颗粒过滤器。

图7 直线腔CW-CRDS台面实验光路图Fig.7 Optical path sketch of CW-CRDS

为了验证充光时间对检测精度的影响,实验中通过设定不同的触发阈值和延迟时间记录衰荡时间。触发阈值起始设定为50 mV,以10 mV为采样间隔采集,一直到信号强度无法满足触发条件140 mV为止,实验采取四次平均模式采样,采样长度为400 μs,记录测量的全过程。在CRDS中,提取衰荡时间最常用的拟合算法是列文伯格-马夸尔特算法(L-M),具有相对较高的拟合精度。L-M算法是利用指数函数y=y0+Aexp(-x/τ)进行非线性拟合,直接得到衰荡时间。表2为设定不同阈值测量100个衰荡过程所需的时间,在阈值为50 mV时,测量100个衰荡过程时间平均为98 s；阈值140 mV时,100个衰荡测量的平均时间增长到388 s,是阈值为50 mV的3.9倍。实验证明,随着触发阈值的提升,采样所需时间在不断增长,采样频率下降。检测精度如图8(a)所示,触发阈值设置为50 mV时,Δτ/τ为0.0116；触发阈值设置为140 mV时,Δτ/τ为0.0083,提升了1.4倍,检测精度得到提高。因此,在设置触发阈值时,应根据具体情况同时兼顾测量频率和测量精度。

表2 不同阈值测量100个衰荡过程所需时间Tab.2 Time of measuring 100 ring-down processes at different thresholds

关断时间及延迟的存在导致了衰荡曲线畸变,对衰荡曲线进行指数拟合的时候会对拟合优度造成过影响,进而影响衰荡时间的计算精度。若对衰荡过程初期的部分数据进行去除[25],将可能对衰荡时间的提取精度有所帮助。定义去除点为过滤区间,去除点的数量为过滤区间的长度,去除法的实质为去除衰荡曲线畸变的前几个点。每次去除衰荡开始的前的10个数据,测量精度结果如图8(b)所示。随着去除点的增加,在去除130个点时,Δτ/τ下降到最低点,拟合精度达到最高。因此,去除点法是提升检测精度的有效方法。

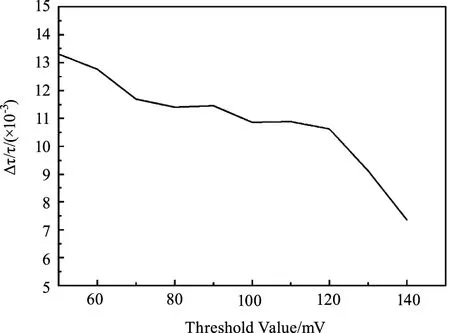
(a)Δτ/τ随阈值的变化图

通过波形发生器来实现关断延迟,设置关断方波信号频率为100 Hz,占空比为2 %,幅值为±200 mV。在单次采样次数下,记录延迟时间从最低设置5 ns起,每次间隔200 ns。图9(a)为随着延迟时间变化的衰荡曲线幅值变化图,图9(b)为其衰荡时间及Δτ/τ变化图。随着延迟时间的增加,从图9(a)中可以看出数据波动逐渐变大,测量阈值范围从200～250 mV增加到160～320 mV,数据一致性变差；图9(b)显示较小的延迟使得Δτ/τ减小,而衰荡时间呈上升趋势,这归因于在到达预设阈值后延迟时间内注入能量大于损耗能量,腔内能量增加,使得检测精度和衰荡时间增加。因此,本实验中,增加适当延迟,可以在较小的数据波动下提升腔内充光能量,进而获得较高的测量精度和衰荡时间,幅值波动和测量精度的的平衡点为延迟400 ns,此时衰荡时间为39.1403 μs,Δτ/τ为0.0162。

(a)

4 结 论

本文分析了连续波腔衰荡测量过程中的腔内能量变化过程,针对充光过程中波长调制,补充了关于激光波长扫描速率的注入光强速率模型,对电流调制失谐关断时的过充现象及数值进行解释分析,完善了衰荡过程全周期模型。在实验中通过改变阈值和延迟时间验证充光时间对检测精度的影响,提升阈值能够有效提高CRDS的测量灵敏度,但衰荡过程的数据获取速率将逐渐降低,因此阈值设定要在满足检测精度的前提下兼顾检测频率；本实验中延迟时间的增加,可在较低数据波动情况下提高衰荡时间和检测精度,二者平衡可以有望高精度采样。