基于磁场调制机理水下电机不平衡力的分析

鲁冰娜，夏加宽，刘津成，马功臣

应用研究

基于磁场调制机理水下电机不平衡力的分析

鲁冰娜，夏加宽，刘津成，马功臣

(沈阳工业大学电气工程学院，沈阳 110870)

不等极弧结构可以有效地削弱电机的齿槽转矩，但会产生不平衡力，针对不等极弧结构电机引起的不平衡力的问题，首先采用解析法推导转子磁动势的谐波分量，并用有限元法对电机的不平衡力进行仿真，其次，对三维结构的模态进行分析，讨论了潜在共振点。然后，基于磁场调制机理对振动进行削弱，结果表明，不等极弧结构能够有效地削弱电机的齿槽转矩，但会产生其他低阶电磁力波，增加电机的振动，不等极弧结构电机改变永磁体形状后，能够显著削弱电机的振动加速度，同时削弱齿槽转矩。

不等极弧系数 不平衡力 齿槽转矩 电机振动

0 引言

永磁同步电机具有转矩密度大、体积小、效率高等优点，已经被广泛应用于水下航行器。随着军事领域的发展，各国对水下航行器的隐蔽性能、勘察能力和控制性能等要求越来越严格，其转矩脉动和电磁噪声已经成为衡量水下电机性能的关键指标。永磁同步电机作为水下航行器的推进电机，其转矩脉动和振动噪声极大地影响着水下航行器的工作性能，其中齿槽转矩是转矩脉动的主要原因，对于转矩脉动的削弱，国内外学者已经研究出很多方法，在文献[1]中采用了斜槽的方法，在文献[2]中采用了斜极的方法，来降低电机的齿槽转矩，其根本原因是在轴向存在相位差，从而减低了齿槽转矩，但是会受电机轴向长度的限制；在文献[3]中对转子采用分段斜极而产生的轴向不平衡磁力进行综合分析，总结了轴向不平衡力的影响因素；在文献[4]中采用分数槽的方法，提高齿槽转矩基波的频率，使齿槽转矩脉动量明显减少。但增加了极数次谐波以及分数次谐波，对电机的振动产生了影响；在文献[5]中通过对极弧系数进行调整来达到降低转矩脉动的目的，但极弧系数过大会引起磁路饱和，并且其效果也没有不等极弧显著；在此基础上本文采用单极不等结构，并从磁场调制机理出发，研究合适的方法来减弱不平衡力。

在文献[6]中李全峰推导了极弧系数相等和不等两种结构下转子磁动势的谐波分布，发现单极极弧系数不等会引入更多转子磁动势谐波分量，使径向电磁力谐波幅值增大，导致振动噪声特性变差。在文献[7]中邢泽智推导了采用不同分段磁极结构时的齿槽转矩解析表达式，给出了最佳极弧系数组合和倾斜角度的确定方法，保证电机正常工作的前提下有效地削弱电机的齿槽转矩。目前采用不等极弧系数的方法并未对其引起的电磁振动进行分析，本文将研究不平衡力引起电机振动的主要原因，并采用合适的方法既能削弱齿槽转矩，又可以抑制其引起的电磁振动，增加电机运行的稳定性，提高电机性能。

1 建模方法

1.1 水下永磁同步电机结构

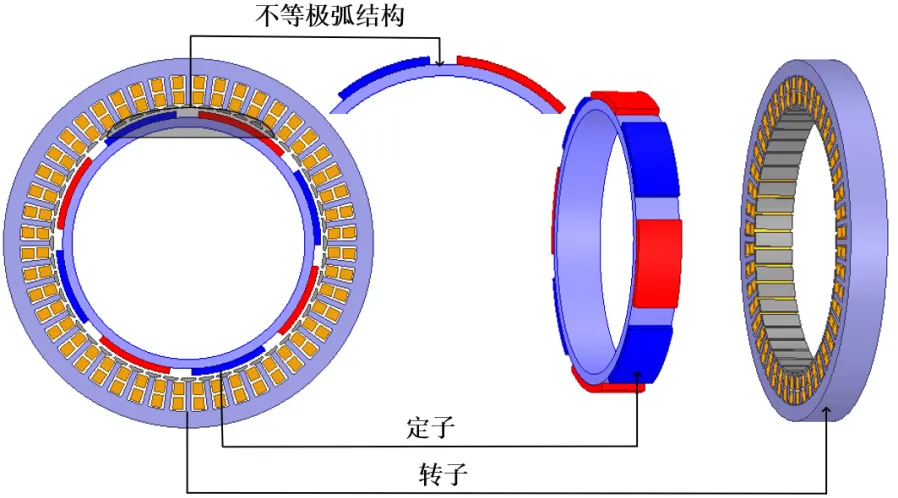
图1 电机模型

表1 水下永磁同步电机电磁参数

本文采用8极48槽电机，电机的基本参数如表1所示，图1显示了水下电机的不等极弧系数结构，其中电机转子采用单极极弧系数不等结构，其他参数不变，整个转子的平均极弧系数仍然是1。

1.2 不平衡力产生原理

电机的结构不对称会引起不平衡力，如电机轴系变形，材料磁化不均匀和采用不等极弧等均会产生不平衡力[8]，本文所研究的不平衡力是由于永磁体极弧系数不等，但永磁体用量与相应的等极弧系数时一致，产生的磁动势幅值一致，但是相应跨距的磁动势反生变化。

当极弧相等时，如图2(a)所示，永磁体产生的磁动势波形函数为：

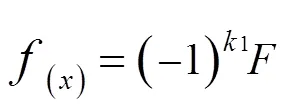
可以看出极弧相等结构转子磁动势谐波只含有基波的奇数次谐波。

当极弧系数不等时，永磁体产生的磁动势如图2(b)所示，可见相应跨距的磁动势反生变化，此时磁动势幅值为：

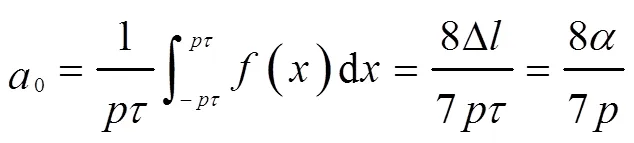
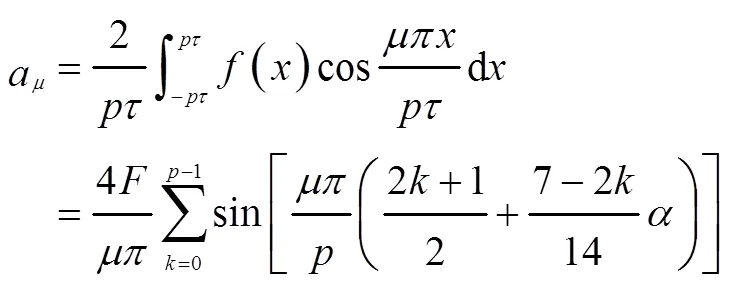
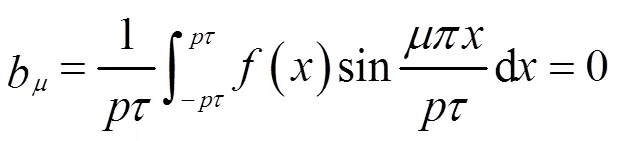
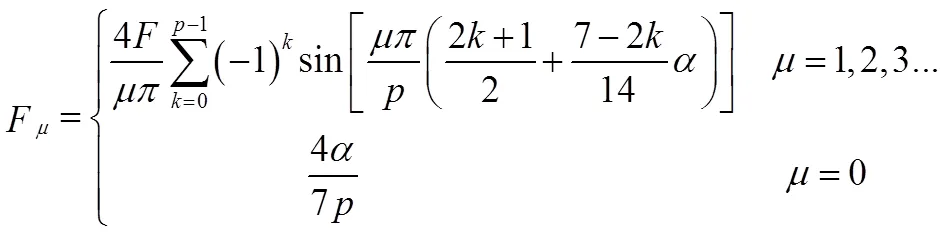
可见，极弧系数不等结构永磁体产生的磁动势波形发生变化，经过傅里叶分解后永磁体磁动势谐波除了基波的奇数次谐波，还会产生其他阶次分数次谐波和偶数次谐波，从而影响电机的径向分量和切向分量[6]。

2 不平衡力分析

2.1 径向电磁力分析

采用麦克斯韦应力张量法计算铁磁材料在磁场中的力。忽略作用于定子齿面的切向分量时，作用在定子磁场的径向力密为[9]：

2.2 有限元分析

建立有限元模型对电机的电磁特性进行仿真，如图3所示电机的磁场密度分布均匀，没有出现过饱和现象。

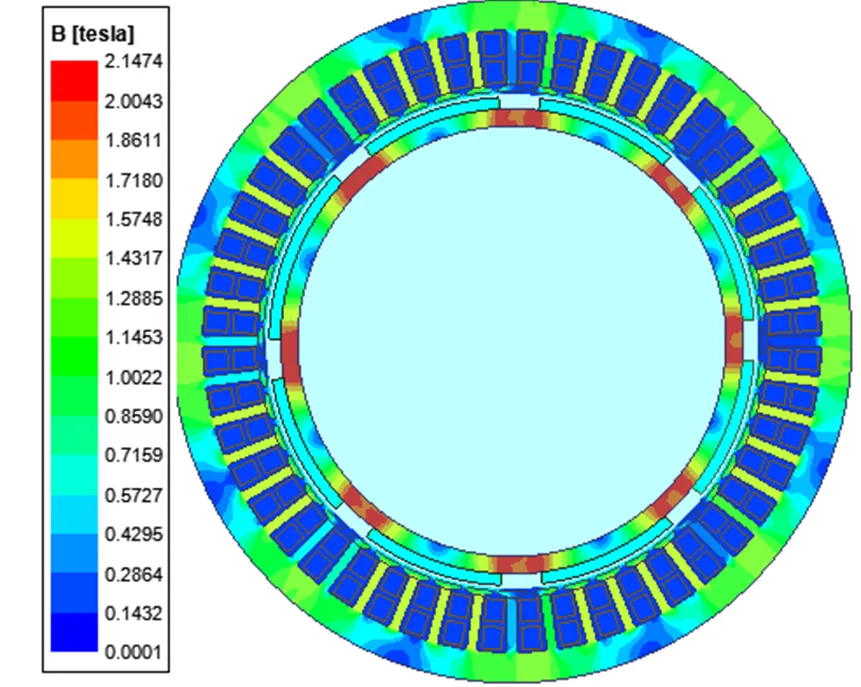
图3 磁密云图

对等极弧系数电机与永磁体用量相同的不等极弧结构的电机进行比较分析，如图4所示，不等极弧系数结构的电机齿槽转矩有显著地降低，齿槽转矩峰值由726.1mNm降低到51.8mNm，大大减小了电机的切向分量，使电机运行更加平稳。如图5所示，气隙磁场密度最大值由0.57T下降到0.47T，略微减小，将其磁场密度进行傅里叶分解，如图6中，主要谐波次数为4、12、20、28次等，其幅值均有所降低，但是会产生其他奇数次谐波，如3、5、7等谐波次数，其幅值并不大。

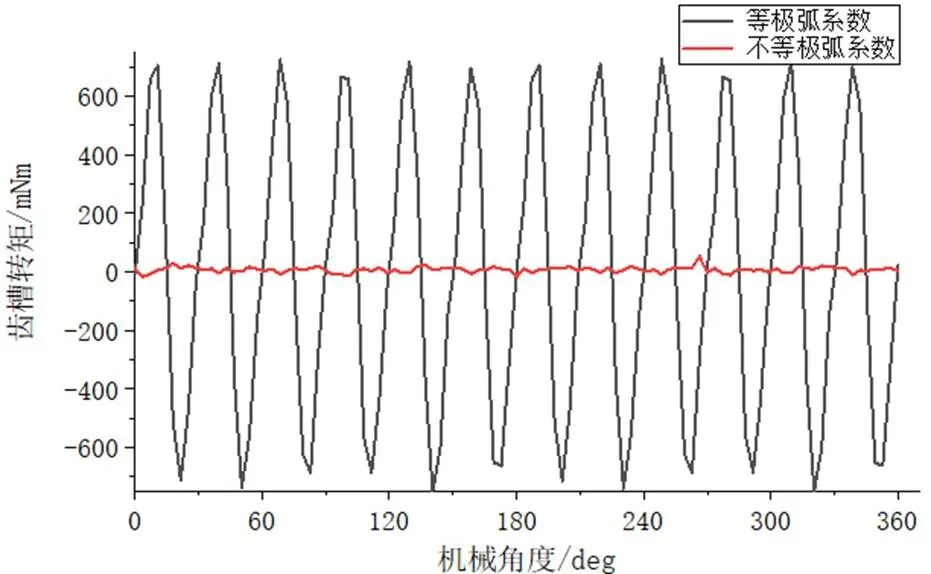
图4 齿槽转矩对比图

图5 气隙磁密对比图

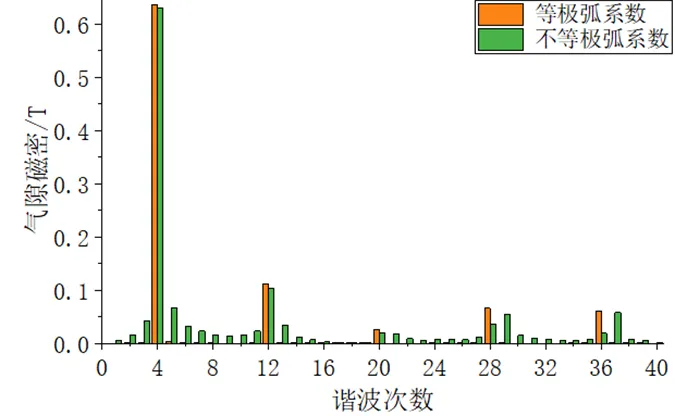
图6 气隙磁密傅里叶分解图

如图7所示，电机径向电磁力密度由96 809.9 N/m2增加到97 525.9 N/m2，进行傅里叶分解后如图8所示，8、16、24、32阶等主要电磁力波降低，此时径向电磁力也包含其他阶次的奇数次电磁力波，但幅值并不大。

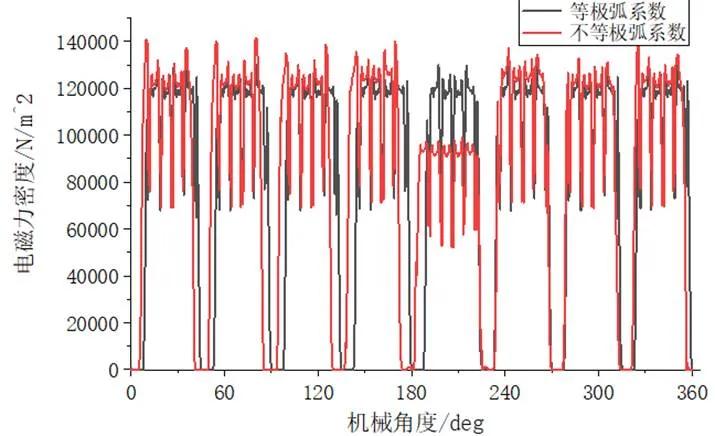
图7 电磁力对比图

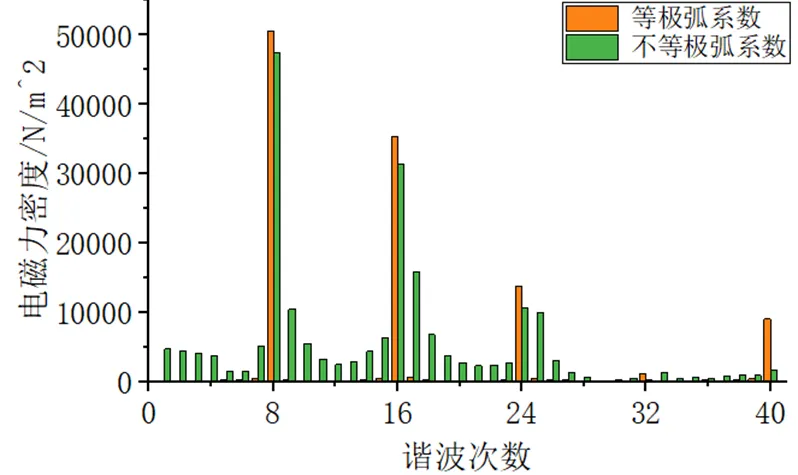
图8 电磁力傅里叶分解图

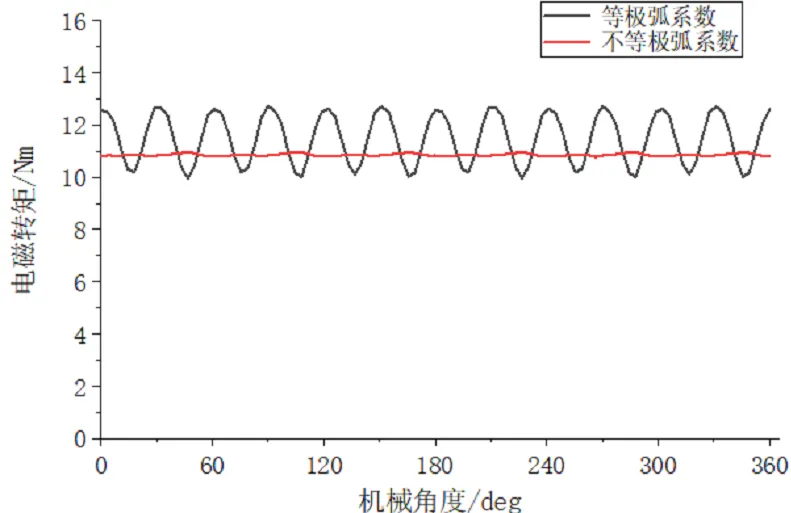
图9 电磁转矩对比图

当电机负载状态下，如图9所示，电磁转矩由原来的11.46 Nm变化到10.86 Nm ，变化范围在5%，对电机的运行性能影响不大。

3 模态与振动分析

3.1 模态分析

在研究永磁同步电机的电磁振动时，不仅要分析径向电磁力波的特性，还要分析其固有频率[12]。因此本文通过观察各阶模态下定子的受力变形，来预测潜在的共振点。

图10为定子铁心结构模态，m为定子铁心在轴向上的受力变形方向，n为径向模态阶次。，结果可知二阶正向模态固有频率为424.17 Hz，反向模态固有频率为837.35 Hz，三阶正向模态固有频率为1 153.4 Hz，反向模态固有频率为5 031.7 Hz，四阶正向模态固有频率为2 104.8 Hz，反向模态固有频率为2 604.9 Hz，八阶模态固有频率为10253.0 Hz，反向模态固有频率为10 360.0 Hz，零阶模态固有频率为5 937.1 Hz，固有频率较低，易发生共振。

由于水下电机在全速范围下运行，因此对电机的频谱图进行分析，图11所示为零阶力波和零阶模态的频谱图，本文电机的主要电磁力波为0阶和8阶力波，由于10 000 Hz以上的电磁振动非常小可以忽略不计，因此只需考虑0阶径向力波和零阶模态的共振。因为8阶模态的频率已在10 000 Hz以外，所以八阶模态对电机影响较小，零阶模态的固有频率为5 937.1 Hz，在转速为2 500 rpm时，零阶模态固有频率与电机的32（为电机的基频）较为接近，会发生共振。

图11 零阶力波和零阶模态的频谱图

3.2 振动特性分析及优化

电机振动波形并不是单一的正弦波，而是由许多不同频率的波形组成。一般而言，电机的振动噪声与力波阶数的四次方成反比，与力波幅值成正比[13]，因而低阶径向力波是引起电磁噪声的主要原因，所以本文通过降低电磁力从而减小电机的振动。对电机的振动进行仿真分析，结果如图12所示，电机在频率为5 916.7 Hz时引起的振动最大，此处较大的振动是由于0阶力波的振动产生，即电机电磁力频率与零阶模态固有频率接近，会产生共振，当电磁力削弱后，能够显著地削弱共振点的振动，其他较为明显的振动是由于电机的12、24等作用产生的。由对比结果可知，不等极弧系数结构的电机虽然能够有效的削弱齿槽转矩，减小电机的切向分量，但径向电磁力其他阶次谐波的产生会使其振动加速度幅值变大，振动加强。

图12 不同极弧结构振动对比

为了让产生的永磁体磁动势更接近于正弦波，改变永磁体形状如图13所示，永磁体磁动势谐波会进一步削弱。

图13 永磁体形状

因此对不同偏心距进行有限元仿真分析，结果如14图，当偏心距分别为0、20、25、30mm时对应的电磁力密度分别为95 212.9 N/m2、86 344.4 N/m2、85 014.9 N/m2、86 482.3 N/m2，齿槽转矩分别为77.7 mNm、36.4 mNm、24.3 mNm、12.8 mNm，结合对径向和切向分量的影响，取偏心距25 mm和30 mm进行优化。

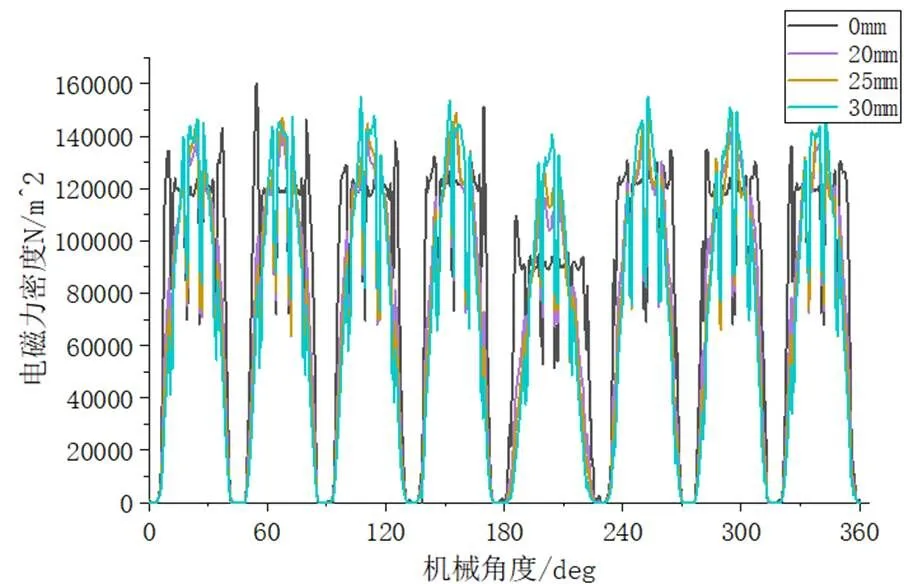
图14 不同偏心距下电磁力密度

优化后电机在偏心距为25 mm时，如图15、16所示，电机产生的齿槽转矩有所降低，同时产生的振动加速度也最小，在此偏心距下电机在5 916.7 Hz时产生的最大振动由1 523.2 mm/s2减小到1 040.2 mm/s2，降低了31%，不等极弧结构改变永磁体形状后能够有效的降低电机的振动加速度，同时削弱齿槽转矩。

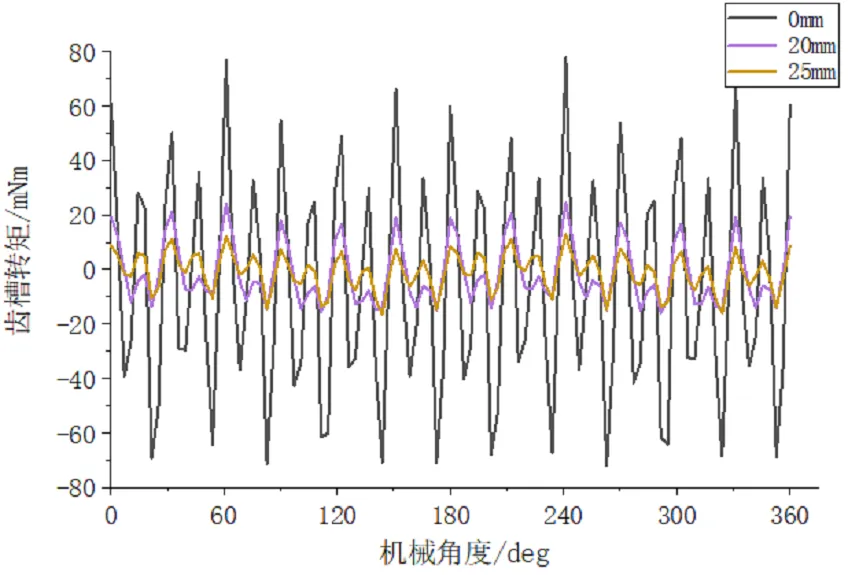
图15 不同偏心距下齿槽转矩

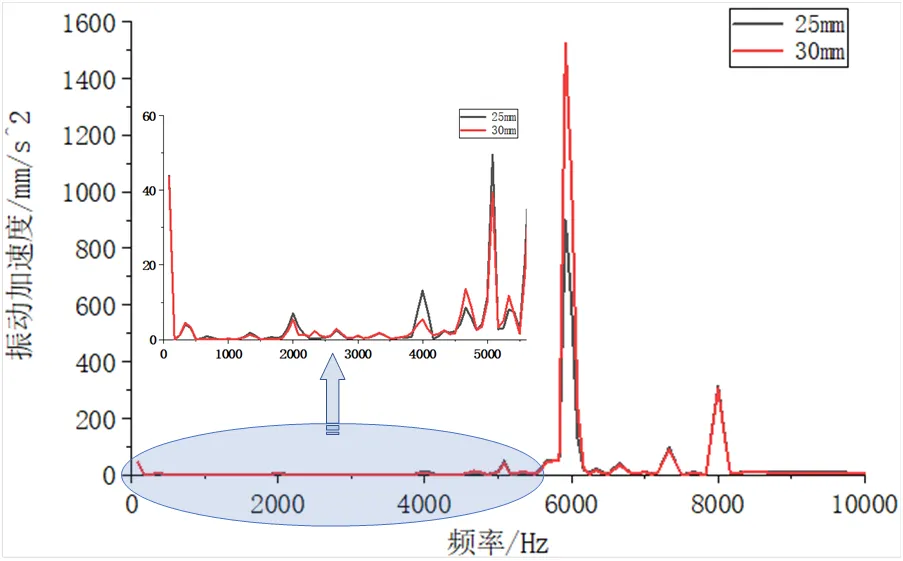
图16 不同偏心距下振动加速度

4 结论

不等极弧结构能够有效地削弱电机的齿槽转矩，能够抑制电机的切向分量作用，但由此产生的不平衡力，会使径向电磁力产生其他低阶电磁力波，从而加大电机的振动，由于改变永磁体形状后，产生的永磁体磁动势更接近于正弦波，永磁体磁动势谐波会进一步削弱，从而减小了电机的径向电磁力谐波分量，降低了电机的振动，本文为不平衡力引起的电磁振动的分析提供了参考。

[1] Han Z, Liu J, Gong C. Influence mechanism on vibration and noise of PMSM for different structures of skewed stator[C]. 20th International Conference on Electrical Machines and Systems, 2017.

[2] 邓秋玲, 黄守道, 刘婷, 等. 永磁电机齿槽转矩的研究分析[J]. 湖南大学学报(自然科学版), 2011, 38(03: 56-59.

[3] 金孟加, 费伟中, 沈建新. 转子分段斜极的永磁同步电机轴向磁力的研究[J]. 电工技术学报, 2013, 28(11): 19-27.

[4] 莫会成. 分数槽绕组与永磁无刷电动机[J]. 微电机, 2007(11): 39-42+81

[5] 王秀和, 杨玉波, 丁婷婷, 等. 基于极弧系数选择的实心转子永磁同步电动机齿槽转矩削弱方法研究[J]. 中国电机工程学报, 2005(15): 146-149.

[6] 李全峰, 黄苏融, 黄厚佳. 不等极弧结构永磁同步电机噪声和转矩特性[J]. 浙江大学学报(工学版), 2018, 52(11): 2210-2217.

[7] 邢泽智, 王秀和, 赵文良. 基于不同极弧系数组合分段倾斜磁极的表贴式永磁同步电机齿槽转矩削弱措施研究[J]. 中国电机工程学报, 2021, 41(16): 5737-5748.

[8] 王晓远, 李志明. 分数槽绕组永磁同步电机不平衡磁拉力的分析[J]. 微电机, 2013, 46(02): 9-12+54.

[9] 陈益广, 韩柏然, 沈勇环, 等. 永磁同步推进电机电磁振动分析[J]. 电工技术学报, 2017, 32(23): 16-22.

[10] Takiguchi M, Sugimoto H, Kurihara N, et al. acoustic noise and vibration reduction of srm by elimination of third harmonic component in sum of radial forces[J]. IEEE Transactions on Energy Conversion, 2015, 30(3):883-891.

[11] Lee S H, Hong J P, Hwang S M, et al. Optimal design for noise reduction in interior permanent-magnet motor[J]. IEEE Transactions on Industry Applications, 2006, 45 (6):1954-1960.

[12] 诸自强, 陈永校. 电机定子固有频率及其模态的有限元分析[J]. 电工技术学报，1987(4)：41-44．

[13] W Shu, L H F. 'Reduction of electromagnetic vibration and noise in permanent magnet motor for evs by optimizing design of rotor based on GPR-PSO Model'[J]. Electr. Eng. Technol., 2020, 15, (3): 12311243.

Analysis of unbalanced force of underwater motor based on magnetic field modulation mechanism

Lu Bingna, Xia Jiakuan, Liu Jincheng, Ma Gongchen

（School of Electrical Engineering Shenyang University of Technology, Shenyang 110870, China）

TM351

A

1003-4862（2022）11-0052-06

2022-03-31

鲁冰娜，（1998-），女，硕士，研究方向：永磁电机电磁振动噪声。E-mail：1983362337@qq.com

夏加宽，男，（1962-），教授，博士生导师，研究方向：永磁电机设计及其控制。E-mail：sygdxjk@163.com