基于神经网络的数据驱动互联电力系统负荷频率控制

陈宗遥 卜旭辉,2 郭金丽

基于神经网络的数据驱动互联电力系统负荷频率控制

陈宗遥1卜旭辉1,2郭金丽1

（1. 河南理工大学电气工程与自动化学院 焦作 454003 2. 河南省煤矿装备智能检测与控制重点实验室（河南理工大学） 焦作 454003）

针对高度复杂的电力系统存在的建模误差和不确定性等问题，该文基于无模型自适应控制算法提出一种不依赖电力系统模型信息的负荷频率控制策略。首先将电力系统的动力学模型抽象为一般的非线性函数，在其I/O数据之间引入时变的伪偏导数，将非线性电力系统等效为动态线性数据模型；然后构建一个径向基神经网络在线估计系统的伪偏导数，并使用优化理论设计数据驱动的负荷频率控制方案，在理论上严格分析了闭环电力系统的稳定性和径向基神经网络估计方法的收敛性；最后在互联电力系统上验证该负荷频率控制方法在不利用模型信息的前提下，能够取得良好的跟踪性能。

互联电力系统 负荷频率控制 无模型自适应控制 径向基函数神经网络 数据驱动控制

0 引言

频率是电力系统运行质量的一个关键因素，负荷侧和发电侧功率失衡会发生严重的频率波动，长期的频率偏差会导致联络线过负荷运转，甚至损害发电机设备。对于大规模的互联电力系统，频率控制是维持频率波动和联络线交换功率偏差处于设定范围内的必要措施。负荷频率控制（Load Frequency Control, LFC）对于保障电力系统安全稳定的运行有着重要的意义和研究价值[1-2]。

在过去的几十年里，研究人员提出了很多LFC策略成果[3-9]。这些LFC方法基于电力系统线性模型进行负荷频率控制器的设计，并且部分工作中使用线性矩阵不等式技术求解控制器的可行增益。它们的控制效果严格依赖预先建立的数学模型以及模型参数的准确性。然而，实际电力系统是一个复杂的非线性系统，各种物理限制和饱和约束使得建立准确的数学模型十分困难。前述基于模型的控制器设计方法在实际应用中遇到很多困难；另一方面，线性矩阵不等式技术也会大大加重控制器的计算负担，并且其增益的可行性又直接受到模型和参数的准确性影响。因此，设计不依赖模型信息的LFC具有重要意义。

数据驱动控制算法能够直接基于电力系统的I/O数据设计负荷频率控制器，避免了预先建模和辨识的过程。在电力系统中引入数据驱动控制算法设计频率控制器极具吸引力和研究价值[10]。现有的数据驱动LFC方案包括同步扰动随机逼近算法[11]、深度强化学习算法[12-13]和无模型自适应控制（Model-Free Adaptive Control, MFAC）算法[14-15]。其中同步扰动随机逼近算法和深度强化学习算法是迭代优化算法，并且其算法的实现需要在闭环电力系统中进行实验并采集数据，不可避免地会加重电力系统处理器的计算负担。而MFAC算法兼顾了自适应能力和在线控制特性，计算负担较小，能够在不使用电力系统模型信息的前提下，实现比较好的调频效果。在MFAC方案的设计过程中[14-15]，将电力系统看作一般非线性模型，使用线性化手段将其等效为含有时变伪偏导数的动态线性数据模型，这就导致了电力系统的物理限制和未建模动态等非线性因素以及变化的负荷扰动会被压缩进时变参数伪偏导数（Pseudo Partial Derivative, PPD）中，其内部十分复杂，致使文献[14-15]中采用的改进投影辨识算法可能无法跟踪电力系统的PPD变化量。

事实上，PPD估计值是否准确直接影响到MFAC控制器的调频效果。文献[16-17]提出了一种基于自适应观测器的PPD辨识算法，但是仅证明了PPD的估计值是有界的，没有分析估计值与真实值之间误差的收敛性。为设计一种合适的PPD估计算法，径向基神经网络以其简单的结构和无限逼近的能力[18-19]成为一种可替代的选择。文献[20]利用径向基函数神经网络（Radial Basis Function Neural Network, RBFNN）的上述优点设计了一种PPD辨识算法，但文献中并没有给出辨识算法的稳定分析，并且RBFNN输入向量只包括控制输入数据，仅更新权重向量，并不适合高度复杂的电力系统。

考虑上述因素，为了弱化LFC控制器设计对电力系统模型精确性的依赖性，本文首先利用实时I/O数据构建一种基于数据的电力系统线性模型，采用RBF神经网络在线估计系统参数PPD；其次，基于MFAC算法设计数据驱动LFC方案（以下简称为RBFNN-MFAC），并且使用李雅普诺夫稳定理论严格分析闭环电力系统的稳定性；最后，在三区域互联电力系统中验证了本文方案的有效性。

1 问题描述

1.1 互联电力系统模型

在互联电力系统中，各个区域之间通过联络线连接，每个区域的频率波动都将影响到与其互联的区域。为了保证频率偏差和联络线功率偏差同时收敛到设定值内，定义每个控制系统的综合输出信号为区域控制偏差信号（Area Control Error, ACE），即

式中相关的电力系统参数和变量定义见表1。

图1 互联电力系统模型

Fig.1 Interconnected power system model

表1 电力系统信号定义

Tab.1 Definition of the power system signal

进一步，将电力系统的动力学方程（2）表述为状态空间方程形式，即

其中

可以将电力系统的模型表述为

1.2 动态线性化方案

综合来看，电力系统可以视为一个高度复杂的非线性系统。为了设计数据驱动的频率控制器，本文首先将LFC未知离散模型通过动态线性化方法等效为线性数据方程。

尽管物理限制和不确定性导致了电力系统的动力学特性是未知的，但是其I/O数据可以量测和储存，并且可以用于控制方案的设计。

证明：由式（6）可得

定义

使用假设1和中值定理，可以将式（9）重新表述为

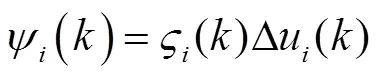
1.3 控制目标

式（8）表明，时变参数PPD中隐含着电力系统不确定因素，其内部十分复杂，无法通过数学表达式精确描述。因此，本文的目标之一是设计某种可靠的估计算法，尽可能使得PPD估计值与实际值之间的估计误差最小。

2 控制方案及稳定性分析

2.1 控制算法

为了设计数据驱动的LFC方案，将动态数据模型（8）写为

考虑如下关于控制输入的准则函数

2.2 PPD估计算法

控制算法（14）的实现需要用到PPD的具体数值，但是其数值未知并且不可精确计算。为此，本文提出一种基于RBFNN的PPD在线估计算法，RBFNN的逻辑结构如图2所示，其中包含一个输入层、一个隐含层和一个输出层，其输出量可以表示为

图2 RBF神经网络结构

参数更新算法为

引入重置条件（25）是为了保证RBFNN-MFAC算法的稳定性。另外，从实际电力系统控制问题的角度来看，任何控制信号必须有界。由于神经网络的估计输出参与控制器的设计，故对其施加合理的限制，令

2.3 稳定性分析

本节从数学角度严格分析算法（式（24）～式（26））的稳定性，首先给出估计过程的收敛性条件定理[21-22]。

其中

将式（20）～式（22）代入式（31），其可以重新表述为

将式（30）代入式（32），可以进一步表述为

定义RBFNN估计算法的李雅普诺夫函数为

因此，上述能量函数的增量可以表达为

将式（33）代入式（35）可得

式（36）表明，随着时间的推移，能量函数逐渐减小，也就是说估计误差最终会收敛到零，RBFNN估计系统是稳定的，证明完毕。

定理2证明了RBF神经网络训练过程是稳定的，实际电力系统闭环回路的稳定性仍需要进一步分析。首先给出以下必要假设：

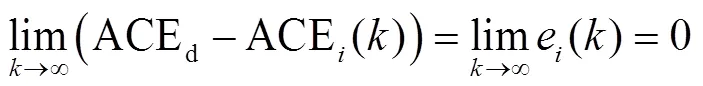
证明：首先，定义闭环电力系统的李雅普诺夫函数为

由式（8）可得

令

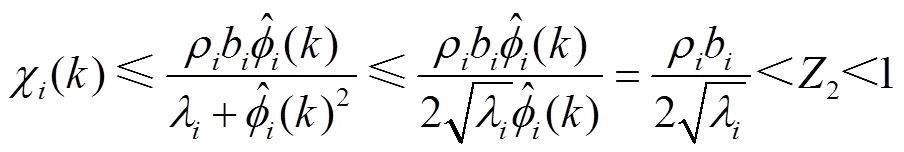
因此，闭环电力系统的李雅普诺夫函数增量可以表述为

本文方法和文献[11]提出的数据驱动LFC方案的主要区别在于：①文献[11]的方法是迭代优化算法，本文方法为在线控制算法；②文献[11]需要在电力系统中采集两次闭环实验数据进行梯度估计，本文并不需要实验过程；③本文方法仅利用电力系统的I/O信息设计数据驱动的LFC方案，没有使用任何模型信息和状态变量。

3 仿真验证

3.1 实验准备

值得说明的是，电力系统的模型和参数在本文设计过程中均假设未知，表1中给出仿真参数仅为产生I/O数据，用以测试本文算法的调频性能，并不决定控制器的结构和增益。

图3 三区域互联电力系统

表2 电力系统仿真参数

Tab.2 Simulation parameters of power system

3.2 常负荷扰动仿真测试

假设在5s时三个控制区域同时受到0.02(pu)的负荷扰动。频率波动和联络线偏差的输出曲线如图4所示。仿真数据表明，本文算法能够很好地处理负荷扰动带来的频率波动问题，显示了理论分析的正确性和本文算法的有效性。

接下来将本文提出的LFC算法与经典MFAC算法[15]、神经元MFAC算法[20]和基于迭代反馈整定（Iterative Feedback Tuning, IFT）优化方案的PI算法的控制性能进行比较，比较结果如图5所示。仿真数据显示本文提出的算法在控制性能上与IFT算法相差无几，并且优于神经元MFAC和经典MFAC控制算法。值得指出的是，IFT算法需要在闭环电力系统中做两次实验进行梯度估计，并且需要迭代收敛的过程，会带来比较繁重的计算负担。而本文算法在性能上与其相仿，但不需要闭环实验和迭代过程，大大降低了控制器的计算量。此外，不同于文献[20]，本文LFC方案使用电力系统的I/O信号作为RBF神经网络的输入数据，直接估计未知的系统参数PPD。仿真对比结果亦显示了本文算法的良好改进效果。

图5 常负荷扰动下对比曲线

3.3 变负荷扰动仿真测试

本节测试改进的MFAC算法在变负荷扰动下的控制性能。图6为变负荷扰动下的频率偏差和联络线功率偏差曲线，负荷扰动变化如图7所示。可以看出在变负荷扰动的干扰下，本文算法仍然具有良好的调频作用，能够将联络线偏差控制在设定范围内，并且调节时间较快，控制效果理想。

图6 变负荷扰动下响应曲线

图7 负荷扰动变化

不同算法的频率偏差控制效果对比如图8所示。相较于经典MFAC和文献[20]改进的神经元MFAC算法，本文方案依然可以兼顾超调量和调节时间的要求，变负荷仿真同样印证了本文算法具有良好的动态性能。

图8 变负荷扰动下对比曲线

3.4 非线性电力系统测试

四种算法的频率偏差对比如图10所示。结果显示，IFT算法不能够很好地应对物理限制因素对调频性能的影响，频率波动较大，而本文提出的LFC策略能够兼顾调节时间和超调量的要求，达到比较理想的调频效果。综合图5和图10的对比数据来看，本文算法的调频性能优于IFT、经典MFAC和神经元MFAC，再一次印证了本文算法具有良好的控制效果和调频性能。

图9 非线性电力系统响应曲线

图10 非线性电力系统对比曲线

4 结论

针对互联电力系统，本文基于RBF神经网络和MFAC算法提出了一种数据驱动LFC策略。该方法弱化了控制器设计对电力系统精确模型的依赖，仅利用其输入输出数据实现负荷频率控制算法的设计。首先引入时变参数PPD，将未知的电力系统等效为一个动态数据模型，并且使用RBF神经网络对未知的PPD进行在线估计。基于此数据模型，设计了数据驱动的RBFNN-MFAC调频方法，使用李雅普诺夫稳定理论对闭环控制系统和PPD估计过程进行严格的收敛性分析。最后在三区域互联电力系统测试算法的实用性和有效性，仿真信息显示本文提出的LFC方法具有良好的控制性能，能够解决复杂的扰动变化带来的频率波动问题，证实了本文算法的有效性。

[1] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804.

Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1791-1804.

[2] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039.

Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.

[3] Liao Kai, Xu Yan. A robust load frequency control scheme for power systems based on second-order sliding mode and extended disturbance observer[J]. IEEE Transactions on Industrial Informatics, 2018, 14(7): 3076-3086.

[5] 杨丽, 孙元章, 徐箭, 等. 基于在线强化学习的风电系统自适应负荷频率控制[J]. 电力系统自动化, 2020, 44(12): 74-83.

Yang Li, Sun Yuanzhang, Xu Jian, et al. Adaptive load frequency control of wind power system based on online reinforcement learning[J]. Automation of Electric Power Systems, 2020, 44(12): 74-83.

[6] 吕永青, 窦晓波, 杨冬梅, 等. 含荷电状态修正和通信延迟的储能电站负荷频率鲁棒控制[J]. 电力系统自动化, 2021, 45(10): 59-67.

Lü Yongqing, Dou Xiaobo, Yang Dongmei, et al. Load-frequency robust control for energy storage power station considering correction of state of charge and communication delay[J]. Automation of Electric Power Systems, 2021, 45(10): 59-67.

[7] 左剑, 谢平平, 李银红, 等. 基于智能优化算法的互联电网负荷频率控制器设计及其控制性能分析[J]. 电工技术学报, 2018, 33(3): 478-489.

Zuo Jian, Xie Pingping, Li Yinhong, et al. Intelligent optimization algorithm based load frequency controller design and its control performance assessment in interconnected power grids[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 478-489.

[8] Bevrani H. Robust power system frequency control[M]. New York: Springer, 2009.

[9] Zhang He, Liu Jun, Xu Shengyuan. H-infinity load frequency control of networked power systems via an event-triggered scheme[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 7104-7113.

[10] 侯庆春, 杜尔顺, 田旭, 等. 数据驱动的电力系统运行方式分析[J]. 中国电机工程学报, 2021, 41(1): 1-12, 393.

Hou Qingchun, Du Ershun, Tian Xu, et al. Data-driven power system operation mode analysis[J]. Proceedings of the CSEE, 2021, 41(1): 1-12, 393.

[11] Dong Na, Han Xueshuo, Gao Zhongke, et al. SPSA-based data-driven control strategy for load frequency control of power systems[J]. IET Generation, Transmission and Distribution, 2018, 12(2): 414-422.

[12] Yan Ziming, Xu Yan. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4599-4608.

[13] Yan Ziming, Xu Yan. Data-driven load frequency control for stochastic power systems: a deep reinforcement learning method with continuous action search[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1653-1656.

[14] 黄伟峰, 姚建刚, 韦亦龙, 等. 无模型自适应控制算法在互联电网AGC中的应用[J]. 电力系统及其自动化学报, 2016, 28(4): 78-84.

Huang Weifeng, Yao Jiangang, Wei Yilong, et al. Application of model-free adaptive control algorithm into AGC control of interconnected power grid[J]. Proceedings of the CSU-EPSA, 2016, 28(4): 78-84.

[15] Asadi Y, Farsangi M M, Bijami E, et al. Data-driven adaptive control of wide-area non-linear systems with input and output saturation: a power system application[J]. International Journal of Electrical Power and Energy Systems, 2021, 133: 107225.

[16] Xu Dezhi, Jiang Bin, Shi Peng. A novel model-free adaptive control design for multivariable industrial processes[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6391-6398.

[17] Xu Dezhi, Jiang Bin, Shi Peng. Adaptive observer based data-driven control for nonlinear discrete-time processes[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(4): 1037-1045.

[18] 王天鹤, 赵希梅, 金鸿雁. 基于递归径向基神经网络的永磁直线同步电机智能二阶滑模控制[J]. 电工技术学报, 2021, 36(6): 1229-1237.

Wang Tianhe, Zhao Ximei, Jin Hongyan. Intelligent second-order sliding mode control based on recurrent radial basis function neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1229-1237.

[19] 付东学, 赵希梅. 基于径向基函数神经网络的永磁直线同步电机反推终端滑模控制[J]. 电工技术学报, 2020, 35(12): 2545-2553.

Fu Dongxue, Zhao Ximei. Backstepping terminal sliding mode control based on radial basis function neural network for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2545-2553.

[20] Su Chengli, Liu Bin, Zhang Guanghui, et al. Application of RBF neural network in the model-free adaptive control[C]//Proceedings of the 2011 Chinese Control and Decision Conference, Mianyang, 2011: 3322-3325.

[21] Yu Qiongxia, Hou Zhongsheng, Bu Xuhui, et al. RBFNN-based data-driven predictive iterative learning control for nonaffine nonlinear systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(4): 1170-1182.

[22] Zhu Yuanming, Hou Zhongsheng, Qian Feng, et al. Dual RBFNNs-based model-free adaptive control with aspen HYSYS simulation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(3): 759-765.

Neural Network Based Data-Driven Load Frequency Control for Interconnected Power Systems

Chen Zongyao1Bu Xuhui1,2Guo Jinli1

（1. School of Electrical Engineering and Automation Henan Polytechnic University Jiaozuo 454003 China 2. Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment Henan Polytechnic University Jiaozuo 454003 China）

To the problems of modeling errors and uncertainties in highly complex power systems, a load frequency control (LFC) strategy was proposed in this paper without using any model information of power system based on model-free adaptive control (MFAC) algorithm. First, the dynamic model of the power system was abstracted as a general nonlinear function. By introducing a time-varying pseudo partial derivative (PPD) between historical I/O data, the nonlinear power system was equivalent to a dynamic linear data model. Secondly, an RBF neural network was constructed to estimate the PPD of the system online, and the optimization theory was used to design the data-driven LFC scheme. In theory, the stability of the closed-loop power system and the convergence of the RBF neural network estimation method were strictly analyzed. Finally, it is verified on the interconnected power system that the LFC method in this paper can achieve good tracking performance without using model information.

Interconnected power system, load frequency control, model-free adaptive control, radial basis function (RBF) neural network, data driven control

10.19595/j.cnki.1000-6753.tces.211208

TM732; TP273

国家自然科学基金（61573130, U1804147）、河南省高校科技创新团队（20IRTSTHN019）、河南理工大学创新型科技团队项目（T2019-2, T2017-1）和河南省创新型科技团队项目（CXTD2016054）资助。

2021-08-04

2021-10-22

陈宗遥 男，1998年生，硕士研究生，研究方向为电力系统的数据驱动控制。E-mail：1556771859@qq.com

卜旭辉 男，1981年生，教授，博士生导师，研究方向为数据驱动控制，电力系统运行控制，网络化控制。E-mail：buxuhui@gmail.com（通信作者）

（编辑 赫蕾）