絮团尺寸对全尾砂絮凝沉降效果的影响研究*

何明渝，王光进，蓝 蓉，李耀基，李全明，宋宁思，刘明生，敬小非，巫尚蔚

(1.昆明理工大学 公共安全与应急管理学院，云南 昆明 650093；2.昆明理工大学 国土资源工程学院，云南 昆明 650093；3.云南省矿产资源开发与固废资源利用国际技术转移中心，云南 昆明 650093；4.昆明有色冶金设计研究院股份公司，云南 昆明 650051；5.云南磷化集团有限公司，云南 昆明 650600；6.北方工业大学 土木工程学院，北京 100144； 7.重庆科技学院 安全工程学院，重庆 401331)

0 引言

随着选矿技术的不断发展，矿石被磨得越来越细，由此产生的尾矿大都具有颗粒细、难沉降等特点。尾矿料浆脱水是尾矿堆存首要环节。因此，常在低浓度矿浆溶液中添加高分子絮凝剂，使尾矿颗粒形成絮团，从而加速沉降，达到固液分离的效果[1]。

絮凝沉降包含复杂的物理化学过程，絮凝剂通常以吸附、架桥等方式将分散的颗粒连接起来，最终形成絮团进行沉降[2-5]。絮凝沉降过程受尾砂料浆浓度、絮凝剂种类、絮凝剂溶液浓度、絮凝剂单耗、初始湍流强度、耙架剪切速率等因素的影响[3，6-8]。

张钦礼等[6]运用BP神经网络和遗传学算法建立全尾砂絮凝沉降参数预测模型，以絮凝剂单耗、尾矿料浆浓度作为输入因子，沉降速度作为输出因子，获得了最佳絮凝沉降参数。苗元丰等[9]以赤泥料浆浓度、絮凝剂种类和单耗为影响因素，分别开展静态沉降和动态沉降实验，最终选出适合该赤泥絮凝沉降的特殊参数值及深锥浓密机工艺参数。高志勇等[10]以尾矿料浆浓度、絮凝剂溶液浓度和用量为影响因素，通过单因素实验，探究各因素对单位面积处理量的影响。周靓等[11]以絮凝剂单耗、絮凝剂溶液浓度和尾砂浆质量浓度为影响因素，以单位面积固体处理能力为考察指标，通过响应曲面分析，确定了全尾砂絮凝沉降最佳参数。Dwari等[12]使用不同聚丙烯酰胺絮凝剂对铬铁砂矿尾矿进行絮凝实验，记录了絮凝剂对沉降速率的影响，得出絮凝剂的离子度和分子量对尾矿沉降性能有显著影响。以上研究多从尾矿料浆浓度、絮凝剂溶液浓度和单耗等着手，通过控制变量或多因素耦合来探究各因素对絮凝沉降速度的影响，从而得出最优絮凝条件，而对全尾砂絮凝沉降过程中絮团尺寸大小对沉降效果影响的研究相对较少。

因此，本文基于多因素耦合下的最优絮凝条件，通过建立絮凝沉降速度模型，借助图像颗粒分析仪(BT-1600)观测各时段絮团尺寸的演变情况，系统分析絮团尺寸变化对絮凝沉降速度的影响，通过非线性拟合，探究絮团尺寸与沉降速度之间的关系。

1 实验

1.1 实验材料

实验全尾砂取自四川某铁矿，其基本物理性能如表1所示。

表1 全尾砂基本物理性能Table 1 Basic physical properties of full tailings

尾矿粒径组成如图1所示。颗粒的不均匀系数为2.5，平均粒径为1.75×10-1mm。

图1 尾矿粒径组成Fig.1 Particle size composition of tailings

絮凝剂为阴离子型高分子絮凝剂—聚丙烯酰胺，相对分子量为1.2×107。

1.2 实验方案

采取正交实验设计方案，以尾砂浆浓度、絮凝剂溶液浓度FF、絮凝剂单耗FD[4]、pH值为变量，研究多因素耦合作用下各因素对尾砂浆固液界面分离高度的影响，实验因素水平如表2所示。通过实验结果，建立沉降速度模型，探究各沉降阶段絮团尺寸变化对沉降速度的影响。

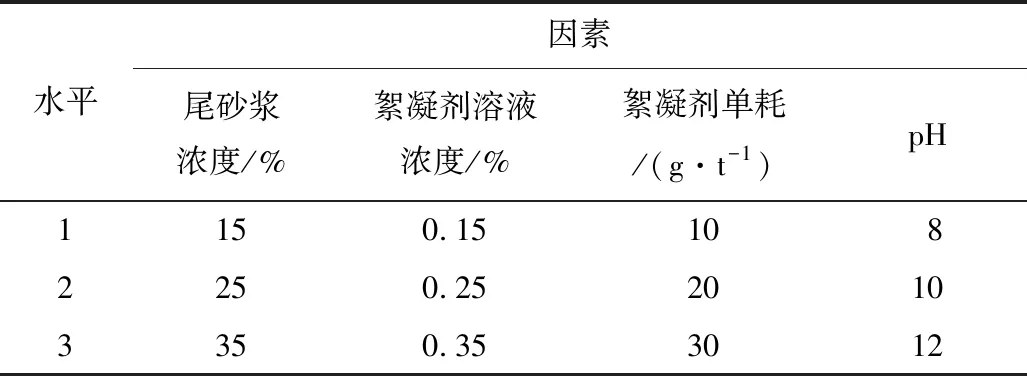
表2 实验因素水平Table 2 Experimental factor levels

2 结果与讨论

2.1 多因素耦合对絮凝沉降速度影响

根据实验方案进行尾砂絮凝沉降实验，并添加3组对照实验。取100 mL量筒，将称量好的全尾砂倒入量筒中，加入一定量水配置成相应浓度的尾砂浆，在各组中加入絮凝剂溶液，上下翻转1圈后静置，记录固液界面分离高度，尾砂絮凝沉降过程如图2所示。由于各组尾砂浆浓度不同，导致量筒内溶液高度不同，因此选择在同一尾砂浆浓度下，分析多因素耦合对尾砂絮凝沉降效果的影响。

图2 尾砂絮凝沉降过程Fig.2 Flocculation and sedimentation process of tailings

当尾砂浆浓度为15%时，尾砂沉降情况如图3所示，前10 s内尾砂浆固液界面分离高度迅速下降，10 s后沉降速度变缓，沉降效果不明显。取反应初期10 s内速度变化值进行分析，以上清液高度为考查指标，建立高度—时间图像并进行线性拟合，以观察各组沉降速度变化情况。由图3可知，在尾砂浆浓度一定的情况下，3组实验中上清液高度随沉降时间的增加而升高。根据实验测得数据1，2，3组在前10 s内的平均沉降速度分别为12.62，13.12，12.72 mm/s，最大沉降高度为131.2 mm。

图3 全尾砂絮凝沉降情况(尾砂浆浓度15%)Fig.3 Full tailings flocculation and settlement (concentration of tailings slurry is 15%)

当尾砂浆浓度为25%时，尾砂沉降情况如图4所示，前10 s内尾砂浆固液界面分离高度迅速下降，通过线性拟合后的高度—时间图像可知，3组实验中上清液高度随沉降时间的增加而升高。根据实验测得数据4，5，6组在前10 s内的平均沉降速度分别为10.15，10.69，8.7 mm/s，最大沉降高度为106.9 mm。

图4 全尾砂絮凝沉降情况(尾砂浆浓度25%)Fig.4 Flocculation and sedimentation of full tailings (concentration of tailings mortar as 25%)

当尾砂浆浓度为35%时，尾砂沉降情况如图5所示，前10 s内尾砂浆固液界面分离高度同样迅速下降，通过线性拟合后的高度—时间图像可知，3组实验中上清液高度随沉降时间的增加而升高。根据实验测得数据7，8，9组在前10 s内的平均沉降速度分别为7.7，5.9，7.35 mm/s，最大沉降高度为77 mm。

图5 全尾砂絮凝沉降情况(尾砂浆浓度35%)Fig.5 Flocculation and sedimentation of full tailings (concentration of tailings slurry as 35%)

2.2 沉降速度模型建立与分析

根据实验结果，选取最优参数组合(W尾砂=15%、FF=0.25%，FD=20 g/t，pH=10)，利用Origin软件对其进行回归拟合，选择Giddings函数[13]，建立沉降速度模型如图6所示。

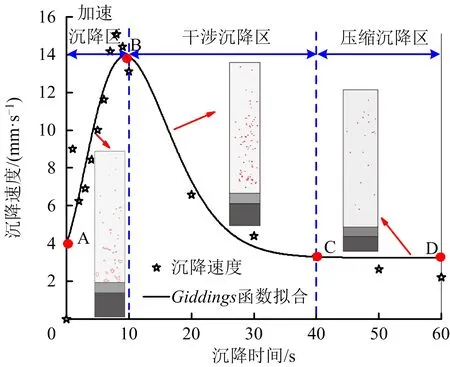
图6 沉降速度模型Fig.6 Model of sedimentation rate

Giddings函数如式(1)所示：

(1)

式中：I1为一阶第1类修正Besse函数；a，b，c，d分别为待回归系数；y为沉降速度，mm/s；x为沉降时间，s。

第1类修正Besse函数Iv(x)如式(2)所示：

(2)

式中：k为求和函数取值；v为修正Besse函数类别。

当v=1时，为一阶第1类修正Besse函数，如式(3)所示：

(3)

通过回归拟合得到沉降速度方程如式(4)所示：

(4)

根据Giddings函数拟合图像，将絮凝沉降过程中速度的变化划分为3个区段：加速沉降区、干涉沉降区、压缩沉降区。

加速沉降区AB段：高分子絮凝剂加入尾砂溶液中，通过“吸附”作用将尾砂颗粒吸附在长链上，多个高分子之间通过“架桥”作用将尾砂颗粒包裹在其中，形成絮团，在重力作用下快速沉降，该阶段反应迅速，一般在数秒内完成。

干涉沉降区BC段：随着絮团不断形成和下降，量筒底部固体浓度不断增大，对向下运动的絮团有一定的排斥力；同时由于溶液中形成的絮团数量增多，絮团之间存在空间位阻效应[8]，颗粒之间相互排斥，因而该阶段溶液中悬浮大量尾砂颗粒，其沉降速度逐渐下降。

压缩沉降区CD段：量筒底部高浓度区域内，絮团之间、絮团内部存在一定量自由水，絮团之间间距较大。在重力作用下，量筒上部的尾砂颗粒继续沉降，逐渐将底部絮团之间的自由水排出，使其得到进一步压缩，底部固体浓度增大。该阶段量筒上部溶液中的尾砂颗粒含量较少，沉降速度缓慢。

2.3 絮团尺寸对絮凝沉降速度影响

利用图像颗粒分析仪(BT-1600)观察不同阶段絮团尺寸变化情况，如图7所示。

图7 BT-1600图像颗粒分析仪Fig.7 BT-1600 image particle analyzer

为方便获取各时间段的絮团尺寸，将系统采集的图像进行图像预处理、图像二值化、图像分割和后处理，以得到絮团的面积、直径、长径比、圆形度等参数值。图像预处理即图像增强，主要包括去背景、转换图像灰度、图像灰度削波处理；图像二值化则将预处理后的灰度图转变为二值图，当对象像素的灰度超过阈值时，被识别为指定目标，灰度值为255，若未超过阈值，则不被识别，灰度值为0[14]，二值化处理表达如式(5)所示：

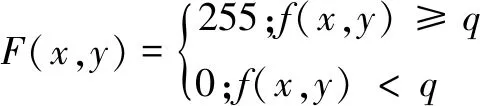
(5)

式中：F(x,y)为二值图像的灰度值；f(x,y)为灰度图像的灰度值；q为设置的阈值。

以絮团直径(D)表征絮团粒径；以圆形度(C)描述颗粒投影面接近圆形的程度，其计算公式如式(6)所示：

(6)

式中：A为颗粒投影面面积，mm2；P1为颗粒投影面周长，mm；C为圆形度。

以长径比Eα描述颗粒投影面的狭长程度，其计算公式如式(7)所示：

(7)

式中：Lmax为颗粒投影面内的最长径，mm；Dmax为颗粒投影面内与Lmax相垂直的最长短径，mm；Eα为长径比。

C越接近1，表明颗粒投影面形状越接近圆形；Eα越接近1，表明颗粒形状越接近圆形或正方形[15-16]。絮团在沉降时间为5，10，20，40，60 s时未处理、预处理及二值化处理后的效果如图8所示。

图8 絮团未处理、预处理及二值化处理效果Fig.8 Effects of untreated,pretreated and binarized flocculation

根据系统处理结果，在各沉降时间段(5，10，20，40，60 s)内选取15个絮团，絮团尺寸(直径、圆形度、长径比)与沉降速度之间的关系如图9～10所示。

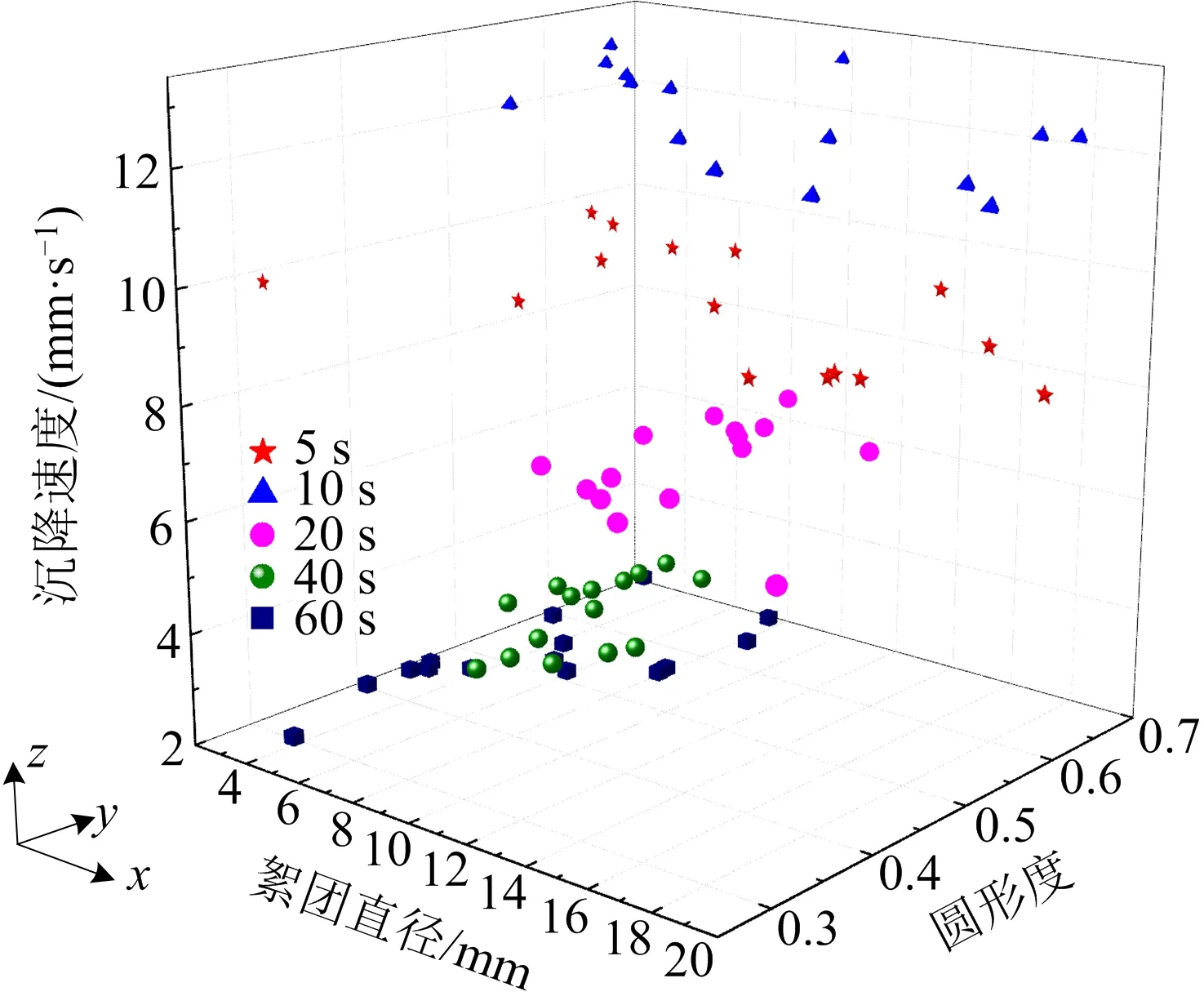
图9 不同时段下絮团直径与圆形度、沉降速度之间的关系Fig.9 Relationship between floc diameter,circularity and sedimentation rate at different time periods

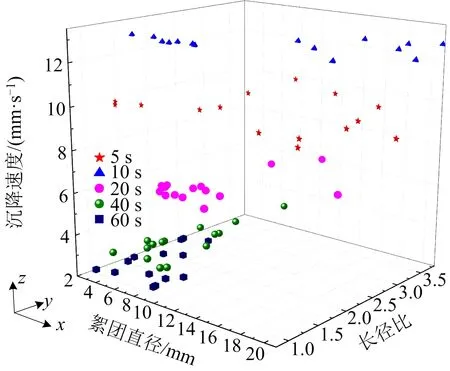
图10 不同时段下絮团直径与长径比、沉降速度之间的关系Fig.10 Relationship between floc diameter,length-diameter ratio and sedimentation rate at different time periods

由图9可知，在xy方向上，圆形度随时间的增加而增大，絮团直径随时间的增加先增大后减小，圆形度与絮团直径之间呈负相关，这是因为随着沉降时间增加，先形成的大颗粒絮团已经沉降，而悬浮在溶液中的尾砂颗粒逐渐减少，存在多个絮凝剂高分子链吸附相同尾砂颗粒的现象，高分子链间的“包裹”作用使得絮团逐渐由层状变为圆形状，絮团直径减小，圆形度增大。

在xz方向上，沉降速度和絮团直径随时间的增加均先增大后减少，沉降速度与絮团直径之间呈正相关，这是由于在反应前期(加速沉降段)生成的层状絮团密度大、沉降速度快，而在反应中期(干涉沉降段)和反应末期(压缩沉降段)生成的圆形状絮团密度小、沉降速度慢所致。

在yz方向上，圆形度随时间的增加而增大，沉降速度随时间的增加而减小，圆形度与沉降速度之间呈负相关，这是因为随着沉降时间的增加，絮团粒径逐渐减小，絮团由层状变为圆形状，圆形度增大，而絮团投影面面积减小、絮团密度降低，导致沉降速度减小。

由图10可知，在xy方向上，长径比和絮团直径随时间的增加均先增大后减小，长径比与絮团直径之间呈正相关，这是因为在反应过程中，先生成的絮团大都为层状、较狭长，因而长径比大、絮团直径也大；随着沉降时间的增加，絮团逐渐变为圆形状，这就使得长径比、直径均减小。

在xz方向上，沉降速度和絮团直径随时间的增加均先增大后减少，沉降速度与絮团直径之间呈正相关，这是由于在反应前期(加速沉降段)生成的层状絮团密度大、沉降速度快，而在反应中期(干涉沉降段)和反应末期(压缩沉降段)生成的圆形状絮团密度小、沉降速度慢所致。

在yz方向上，长径比和沉降速度随时间的增加均先增大后减小，长径比与沉降速度之间呈正相关，这是因为随着沉降时间的增加，絮团直径逐渐减小，长径比越来越接近1，絮团形状接近圆形，絮团包裹的尾砂颗粒减少、密度降低，其沉降速度随之减小。

2.4 基于絮团尺寸的絮凝沉降速度模型

鉴于絮团沉降速度与絮团尺寸有明显相关性，分析絮团在各时段的平均直径、圆形度、长径比与沉降速度之间的关系，建立基于絮团尺寸的絮凝沉降速度模型。

絮团直径与沉降速度之间呈正相关关系，根据图11中各时间段平均直径与沉降速度的分布，建立基于絮团平均直径的沉降速度模型如式(8)所示：

y=-0.760+0.413x1+0.089x12

(8)

式中：x1为平均直径，mm。

图11 沉降速度与絮团平均直径的关系Fig.11 Relationship between sedimentation rate and average diameter of flocs

絮团圆形度与沉降速度之间呈负相关关系，根据图12中各时间段平均圆形度与沉降速度的分布，采用Slogistic1函数，建立基于絮团平均圆形度的沉降速度模型如式(9)所示：

(9)

式中：x2为平均圆形度。

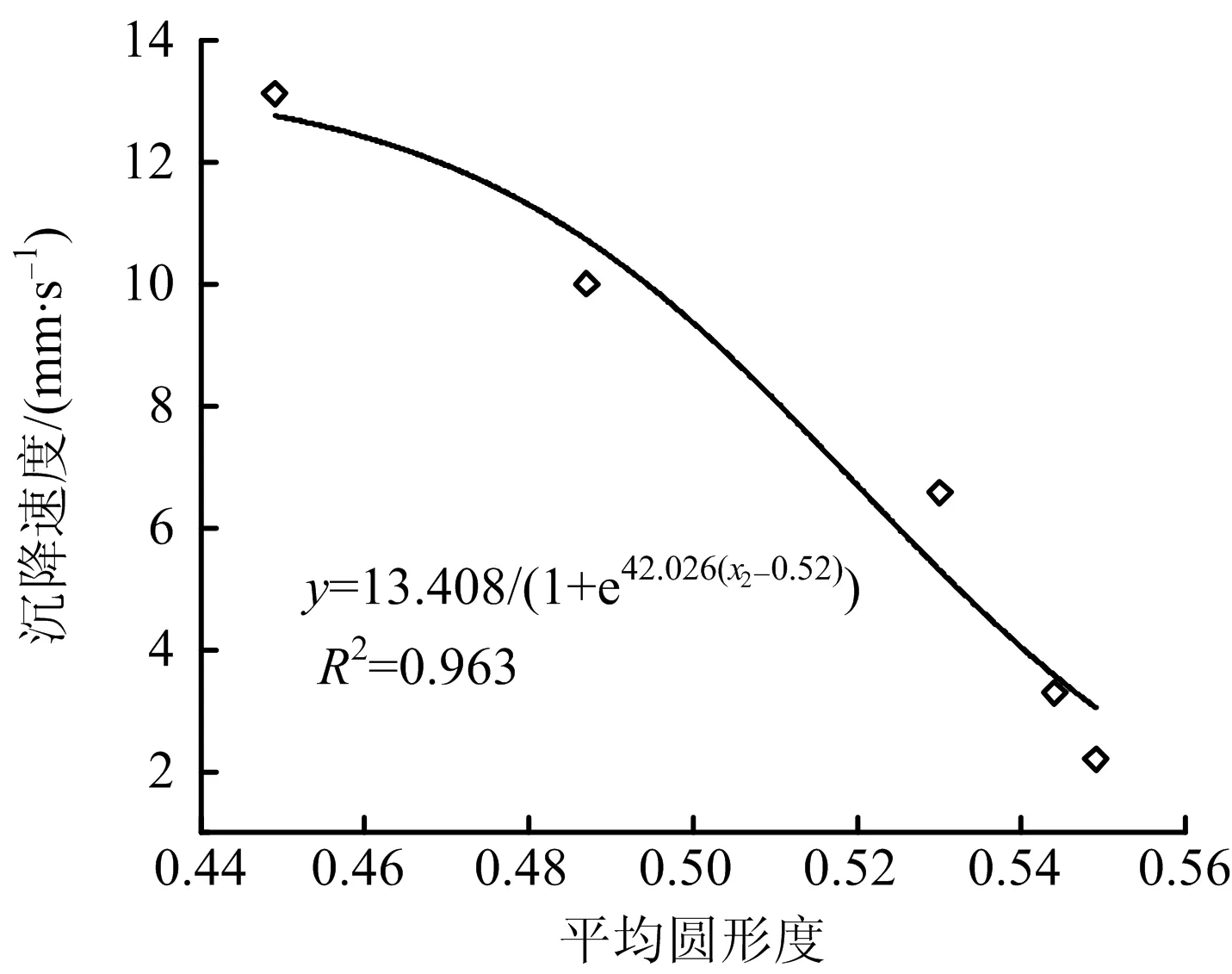
图12 沉降速度与絮团平均圆形度的关系Fig.12 Relationship between sedimentation rate and average circularity of flocs

絮团长径比与沉降速度之间呈正相关关系，根据图13中各时间段平均长径比与沉降速度的分布，采用Boltzmann函数，建立基于絮团平均长径比的沉降速度模型如式(10)所示：

(10)

式中：x3为平均长径比。

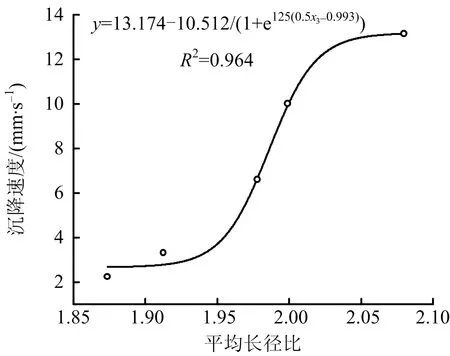
图13 沉降速度与絮团平均长径比的关系Fig.13 Relationship between sedimentation rate and average length-diameter ratio of flocs

从基于絮团尺寸的絮凝沉降速度模型中，不难看出絮团直径、圆形度、长径比对沉降速度都有显著影响，在絮团直径、长径比较大，圆形度较小的情况下，沉降速度可达到峰值，对应沉降速度模型中自由沉降区的最高点。因此，在实际生产中，可通过控制沉降时间，使絮团尺寸达到最佳状态，从而提高絮凝沉降速度。

根据实验获得的最优絮凝条件，对四川某铜矿尾矿进行了相同条件下的絮凝沉降实验，发现絮团尺寸变化和沉降速度之间有着相同的变化规律，因此，本文的实验结论在其他矿种尾矿中有一定推广性。

3 结论

1)确定多因素耦合条件下最优絮凝条件：尾砂浓度为15%、絮凝剂溶液浓度为0.25%、絮凝剂单耗为20 g/t，溶液pH为10，在自由沉降区(0～10 s)的最终沉降高度为131.2 mm，沉降速度可达13.12 mm/s。

2)基于最优絮凝条件，建立基于Giddings函数的沉降速度模型，将絮凝沉降过程分为3个区段：自由沉降区、干涉沉降区、压缩沉降区。在自由沉降区，沉降速度随时间的增加而增大；在干涉沉降区和压缩沉降区，沉降速度随时间的增加而减小。

3)借助图像颗粒分析仪(BT-1600)探讨絮团尺寸变化与沉降速度的关系：随着沉降时间的增加，沉降速度随絮团直径的减小而减小；随絮团圆形度的增大而减小；随长径比的减小而减小。

4)基于Slogistic1，Boltzmann等函数，建立适用于该全尾砂的基于絮团尺寸的沉降速度模型，该模型可为实际生产中提高尾砂絮凝沉降速度提供一定参考。