基于Jaya优化标定的高精度数据采集方法

张合生焦鹏胡琪睿蔡江乾胡顺波曹贺欧阳求保

(1.上海大学机电工程与自动化学院,上海200444;2.上海大学计算机工程与科学学院,上海200444;3.上海大学材料基因组工程研究院材料信息与数据科学中心,上海200444;4.之江实验室,浙江杭州311100;5.上海交通大学材料科学与工程学院金属基复合材料国家重点实验室,上海200240)

高纯材料和高性能铝基复合材料是先进功能材料和先进结构材料及其关键构件生产、研制的基础[1].在航天、空间、微电子领域,对先进功能材料纯度以及先进轻量化结构材料综合性能的要求越来越高[2-4].相应地,对先进功能和结构材料生产工艺的要求也越来越高[5-6],甚至需要实时获取设备生产的相关工艺参数数据,从而对设备数据进行综合分析后及时调整工艺参数,以实现对工艺的优化,如铝基复合材料制备过程中涉及的熔炼复合设备、粉末冶金设备、热处理设备,都需要对关键工艺参数进行实时高精度数据采集.由于大量现有设备没有信息化数据接口[7],只能附加一套高精度数据采集系统来实现实时数据采集.要实现高精度数据采集,在确定数据处理模型的基础上,必须实现高精度数据标定.在数据标定实施过程中,由于原设备数据采集与新增的数据采集系统周期不一致,设备显示值和数据采集值在时间上存在随机误差,若直接进行数据标定,必然导致数据处理参数存在相对较大误差,并最终影响数据采集系统的采集精度.因此,数据处理参数的高精度标定技术成为构建高精度数据采集系统的关键.

采集系统处理参数的标定本质上是建立采集值(输入值)和目标值(输出值)之间的数学模型,并求解该数学模型的参数值,属于参数求解问题[8-10].传统数据标定方法有最小二乘法拟合法,虽然最小二乘法较为简单、效率高,但只能确定一组原始参数,不能解决本工作所涉及的数据时间不同步的问题.近年来,采用优化算法搜索最优参数成为新的研究热点,傅恺延等[11]针对交通仿真模型参数难以确定的问题,采用一种交叉熵算法来寻找最优参数;田少兵等[12]针对相机标定问题,将相机内参值作为初始值,提出了一种改进粒子群算法的相机内参数标定算法[12];吴桂芳等[13]采用差分进化算法对三维电场传感器解耦进行标定.传统的寻优算法往往需要多个特殊参数,增加了优化过程的复杂性.Rao[14]提出了一种无需特殊参数的Jaya算法,该算法是新颖的群体智能算法,常用于解决约束和无约束优化问题.但不同于粒子群优化(particle swarm optimization,PSO)、洗牌青蛙跳跃(shuffled frog leaping,SFL)、萤火虫(firefly,FF)算法等常见群体智能优化算法,Jaya算法不需要控制专属于算法的特殊参数,仅仅需要控制若干共有参数,如种群个数及迭代次数等[15-16],因而与其他群体智能算法相比,Jaya算法可以较大程度地降低求解的复杂性,在参数求解的精确度与复杂度之间达到较好的平衡.

本工作在数据采集系统设计基础上,针对数据采集值和真实值时间不同步的问题,基于Jaya优化算法,对数据处理模型参数进行了优化标定;对Jaya算法进行了仿真实验验证,并以设备温度数据采集为例进行了实际测试和验证.结果表明,本工作所提出方法具有较好的标定效果,可实现数据的高精度实时采集.

1 数据采集系统设计

本工作设计的高精度数据采集系统采用分布式结构,由若干子系统组成.各子系统负责采集所在区域设备数据,基于以太网技术实现整个采集系统网络构建和子网扩展,用交换机将各数据采集子网组成局域网,通过数据库技术实现数据采集服务接口,使得子系统将采集好的数据经由网络上传至数据库(数据服务器).高精度数据采集系统结构如图1所示.

对于图1中某个子系统,各设备通过专属数据采集器实现数据采集,采集器之间通过RS485现场总线相连,通过现场数据管理服务软件实现子系统数据收集,现场数据服务器同时负责将子系统的数据传送至数据库.

2 基于Jaya算法的模型参数标定

为提高数据采集精度,数据采集系统的数据处理模型参数采用多点标定的方法,每个标定点包括一个测量值和一个真实值.若将采集设备工作区间的数据分为L段进行标定,且每个区间的模型参数个数为R,则段数和标定点的关系如图2所示.

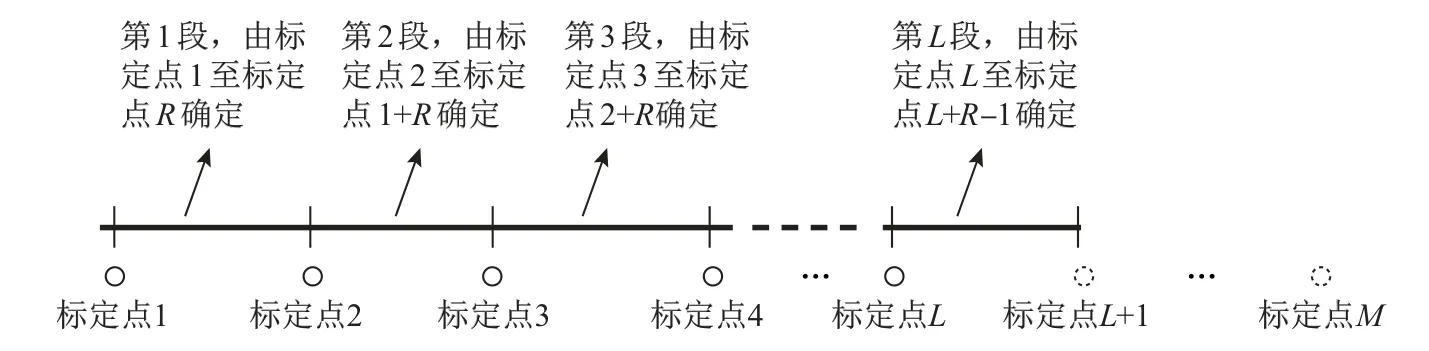
图2 模型区间个数与标定点数量Fig.2 Number of model intervals and the number of calibration points

图2中,每段区间的模型参数都由R个标定点所决定;标定点的总数量M=L+R-1;标定点L+1至标定点M为标定模型区间之外的点,用以确定最后一段模型参数;标定模型区间内的标定点以实线圆表示,区间之外的标定点以虚线圆表示.

若数据采集系统测量值与真实值的关系为f,则第j段模型为

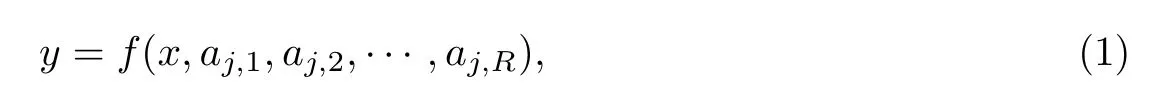
式中:j∈[1,L];x为测量值;y为真实值;aj,r表示第j段的第r个模型参数,r∈[1,R],R为模型参数个数,其大小由模型本身决定.例如,对于线性模型,R为2,则

基于Jaya优化算法可实现最优模型参数搜寻.Jaya算法是一种群体智能优化算法,其种群由一系列个体组成,若种群规模为N,则种群Z为

式中:Xi表示Z的第i个个体,i为个体序号,i∈[1,N],每个个体都代表标定寻优的一组解所对应的标定点测量值.由于在分段标定中共有M个标定点,因此每个个体由M个参数组成,这些参数称为个体变量,

式中:Xi,k表示Xi的第k个个体变量,k为个体变量序号,k∈[1,M].

由于种群的每个个体都决定了一组解,因此种群个体的初始值应当在标定点的测量值附近;另一方面,对于Jaya优化算法,为更好地寻优,种群个体的初始状态应当具有随机性.综合上述两方面原因,种群个体初始化即个体变量初始化,可采用在标定点测量值基础上叠加一个随机数的方法,

式中:p为(-b,b)范围内的随机数,(-b,b)代表了寻优算法的搜索空间,b的大小依据采集系统实际情况确定,如被采集物理量类型、变化范围等,且Xi中的M个个体变量在叠加随机数后的值互不相同.

依据Xi的个体变量和式(1)的处理模型,可建立求解Xi的第j段模型参数方程组:

式中:Xi,j代表第i个个体的第j个变量;yi,j为Xi,j对应的真实值;ai,j,r表示Xi的第j段区间的第r个模型参数.由于模型参数个数为R,因此模型参数必然由R个标定点来决定,且这些标定点一般为连续的标定点;将这些标定点代入式(1)便可得式(6)方程组;解方程组,便可求出Xi第j段模型参数{ai,j,1,ai,j,2,···,ai,j,R}.对于线性模型,式(6)则具体化为

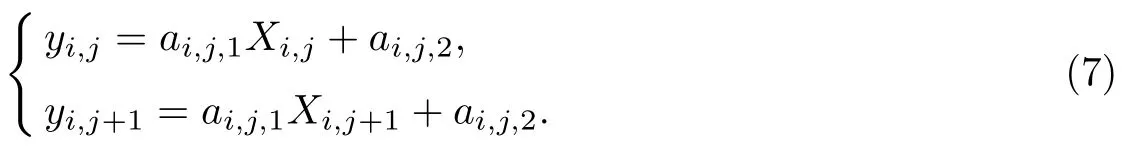
解式(7)方程组可得

得到模型参数后,用验证数据集计算个体的目标函数,并作为寻优过程中个体变量调整的依据.设每个标定段内有E对验证数据,一对验证数据包含一个测量值及一个真实值,则总验证数据对的数量D=EL.

在Jaya算法中,个体的目标函数值是个体变量调整的依据.下面以个体Xi为例进行目标函数构建.首先,考虑Xi的第j段区间,利用式(6)求出该段区间模型参数后,便可利用该模型参数处理验证数据集中属于该区间的原始测量值,

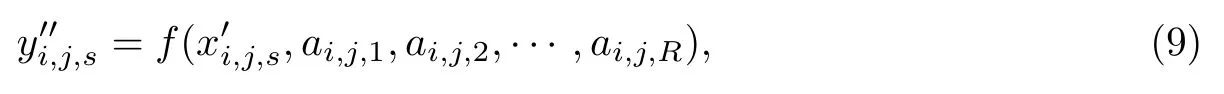
式中:x′i,j,s为Xi第j段区间的第s个验证数据原始测量值;y′′i,j,s为x′i,j,s经模型参数处理后的值.根据式(9),针对第j段区间,可求得误差平方和为

式中:y′i,j,s为x′i,j,s所对应的真实值;Yi,j为个体Xi第j段区间验证数据集误差平方和.依据式(10),对Xi在所有区间的误差平方和求和后,再除以验证数据集点数,得到Xi所有验证点误差平方和的平均值,并作为Xi的目标函数Yi,

根据式(11)计算出种群中所有个体的目标函数值,将目标函数值最小的个体作为最优个体,记为Xbest;将目标函数值最大的个体作为最差个体,记为Xworst.依据Jaya优化算法,可得种群个体更新函数,

式中:Xi,k(t)为当前时刻Xi,k的值;Xi,k(t+1)是更新后下一时刻Xi,k的值;r1,k、r2,k是两个在(0,1)范围内的随机变量;r1,k(Xbest,k(t)-|Xi,k(t)|)表示当前个体向最优个体靠近的趋势;-r2,k(Xworst,k(t)-|Xi,k(t)|)表示当前个体远离最差个体的趋势.

在算法迭代过程中,若迭代次数超过设定上限v,或者种群中最优个体的目标函数为0时,终止寻优过程,并利用最优个体变量计算本次最终优化模型参数.

上述算法流程如图3所示.

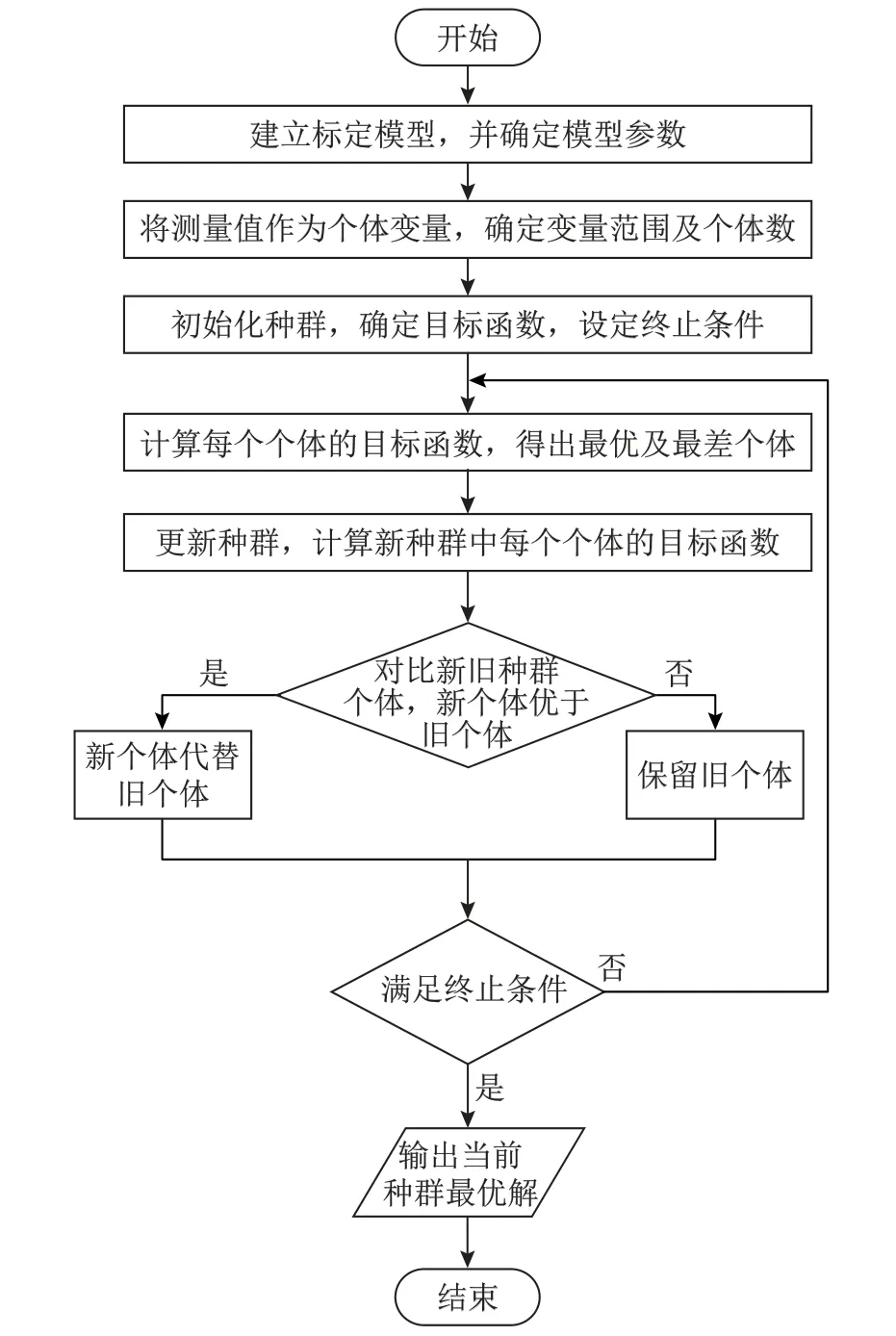
图3 基于Jaya求解标定模型参数算法流程图Fig.3 Algorithm flowchart of solving calibration method parameters based on Jaya

由图3可知,在确定模型参数、种群个体数、个体变量、目标函数、终止条件后,先计算每个个体的目标函数,得出最优及最差个体,通过式(12)更新种群;然后计算新种群中每个个体的目标函数并对比新旧种群个体,用新种群的优秀个体替代旧种群的个体,生成一个由优秀个体组成的新种群,不断进行迭代,直至满足终止条件,输出当前种群最优个体,并通过式(6)求出模型参数.

3 实验验证及数据分析

为验证本工作算法的可行性与有效性,首先进行仿真实验,并以生产现场中的温度采集设备为例,验证算法的真实标定效果.

3.1 基于Jaya算法的模型参数标定仿真实验

首先,仿真模拟一条温度曲线,曲线模型为

式中:t为时间;T0为初始温度;T为t时刻温度.

假设设备工作温度区间为10～200°C，t时刻为0时的T为10°C,即T0=10°C;并假定测量值与真实值(理论值)之间的关系为线性模型.为保证数据采集精度,对工作温度区间进行分段处理,共分为19段,有20个端点值;定义一组(20个)对应于真实值的测量真值的端点值,使每一段的线性模型都确定了唯一一组理论模型参数aj,1、aj,2.将每一段区间的中点作为验证数据,通过理论模型参数确定对应的测量真值,并将所得的最优解与测量真值之间的平均误差作为评价算法性能优劣的指标(见表1).

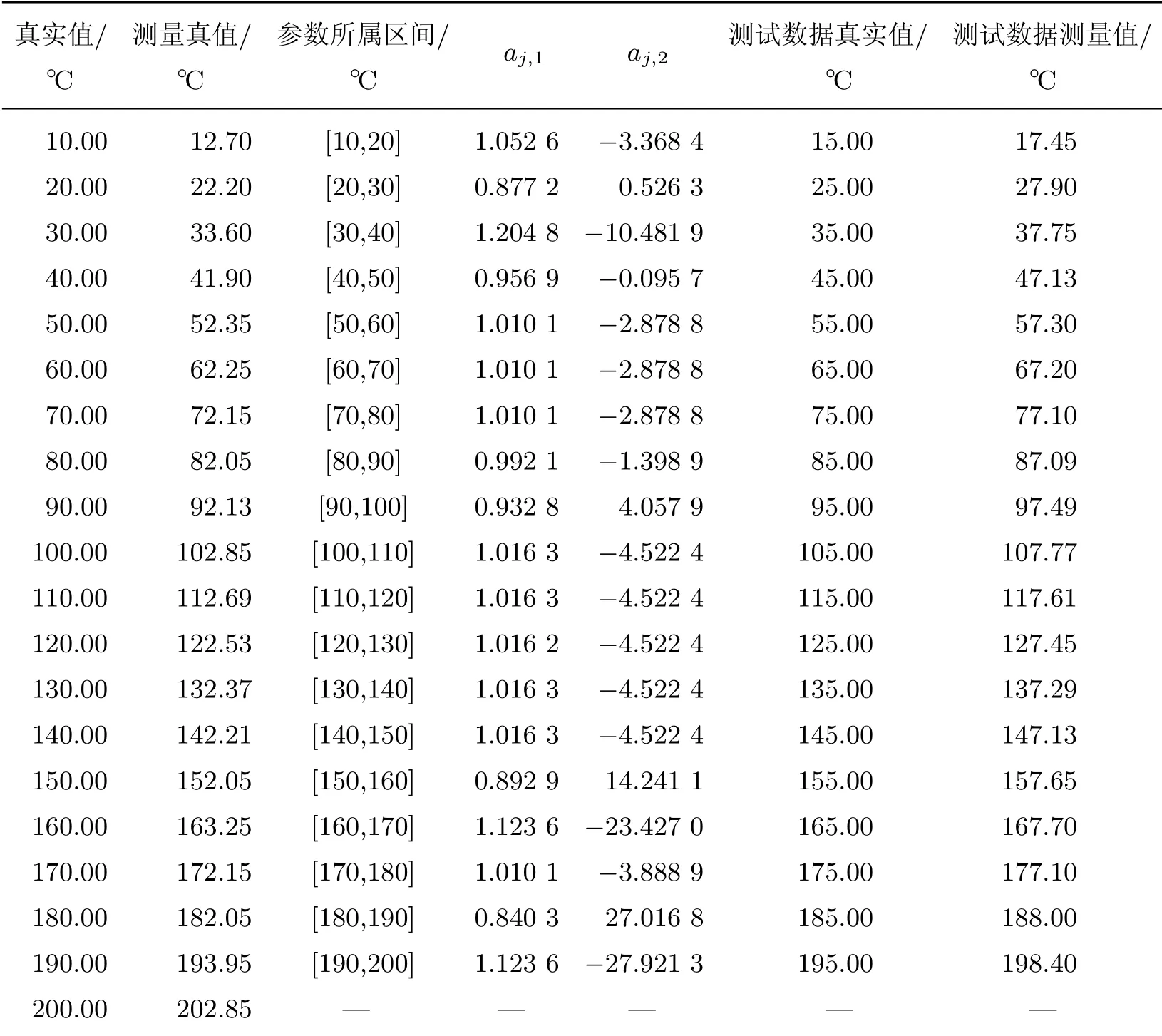
表1 基于Jaya算法的模型参数标定仿真数据Table 1 Simulation data of data calibration method based on Jaya algorithm

仿真实验参数如下:个体数N为50;个体变量数M为20;验证数据对数D为19;终止条件v为4 000次;个体变量为测量值,取值范围为测量真值±1°C.利用每一次种群中的最优个体与真实值求出模型参数,对测试数据的测量值进行处理,以处理后的测量值与测量真值的误差定义目标函数,目标函数越小,则说明该算法寻找到的测量值越接近测量真值,求出的参数越接近理论模型参数.

图4为某次寻优实验的最优个体目标函数值变化趋势.由图4可知,随着迭代次数的增加,约在迭代380次后,目标函数值快速收敛于0°C附近.达到终止条件后得到最优个体,该个体与测量真值的对比分析结果如图5所示.

由图5可知,寻优后的测量值接近于测量真值,平均误差仅为0.008 4°C,精度为99.93%,可见该标定算法具有较高的标定精度.根据式(6)求出该个体的模型参数(优化模型参数),将其与理论模型参数进行对比,结果如图6所示.

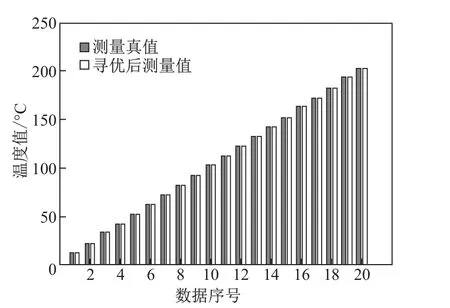
图5 寻优后的测量值与测量真值对比Fig.5 Comparison of the measured value after optimization with the measured truth value

图6 优化模型参数与理论模型参数对比Fig.6 Comparison of optimized model parameters with theoretical model parameters

图6中黑色直线段为线性模型的理论值,红色直线段为线性模型的寻优值.显然,理论模型与寻优模型基本重合,由此可知本工作所提算法是可行的、有效的.为验证算法稳定性,进行了多次寻优,每一次寻优都得到基本相同的结果,说明本工作所提算法具有较好的稳定性.

3.2 基于Jaya算法的模型参数标定测试实验

在实际材料制备过程中,现场温度数据对材料性能具有至关重要的作用,以设备温度采集为研究对象进行实际实验验证.与仿真验证实验相同,处理模型同样采用线性模型.实验过程如下:首先,采集2组温度数据,每组数据包含一系列真实温度数据和采集温度数据;将第一组温度数据作为标定数据点,以确定线性模型参数规模;将第二组数据作为寻优目标函数的计算依据.实际实验中将第一组数据,即每个标定点测量值±1°C作为模型参数的寻优范围.相关温度数据如表2所示.测试实验参数如下:个体数N为50;个体变量数M为13;验证数据对数D为12;终止条件v为4 000次.通过实验获得最优模型参数后,再采集一组数据作为模型参数精度的验证数据(见表3).当达到终止条件后,得到最优个体,通过式(6)求解出最优模型参数(见表4).

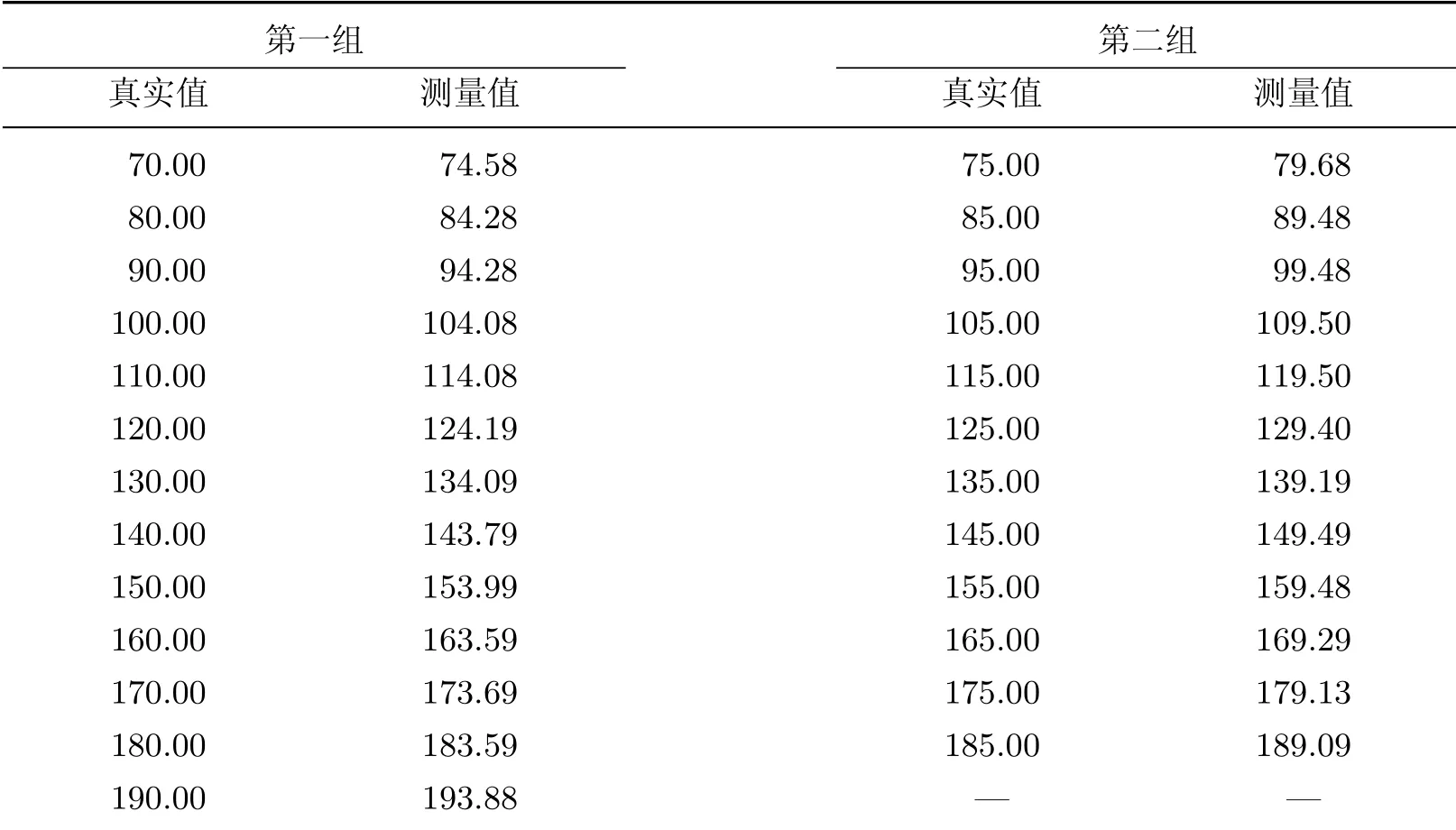
表2 现场设备温度采集数据Table 2 Field device temperature acquisition data °C

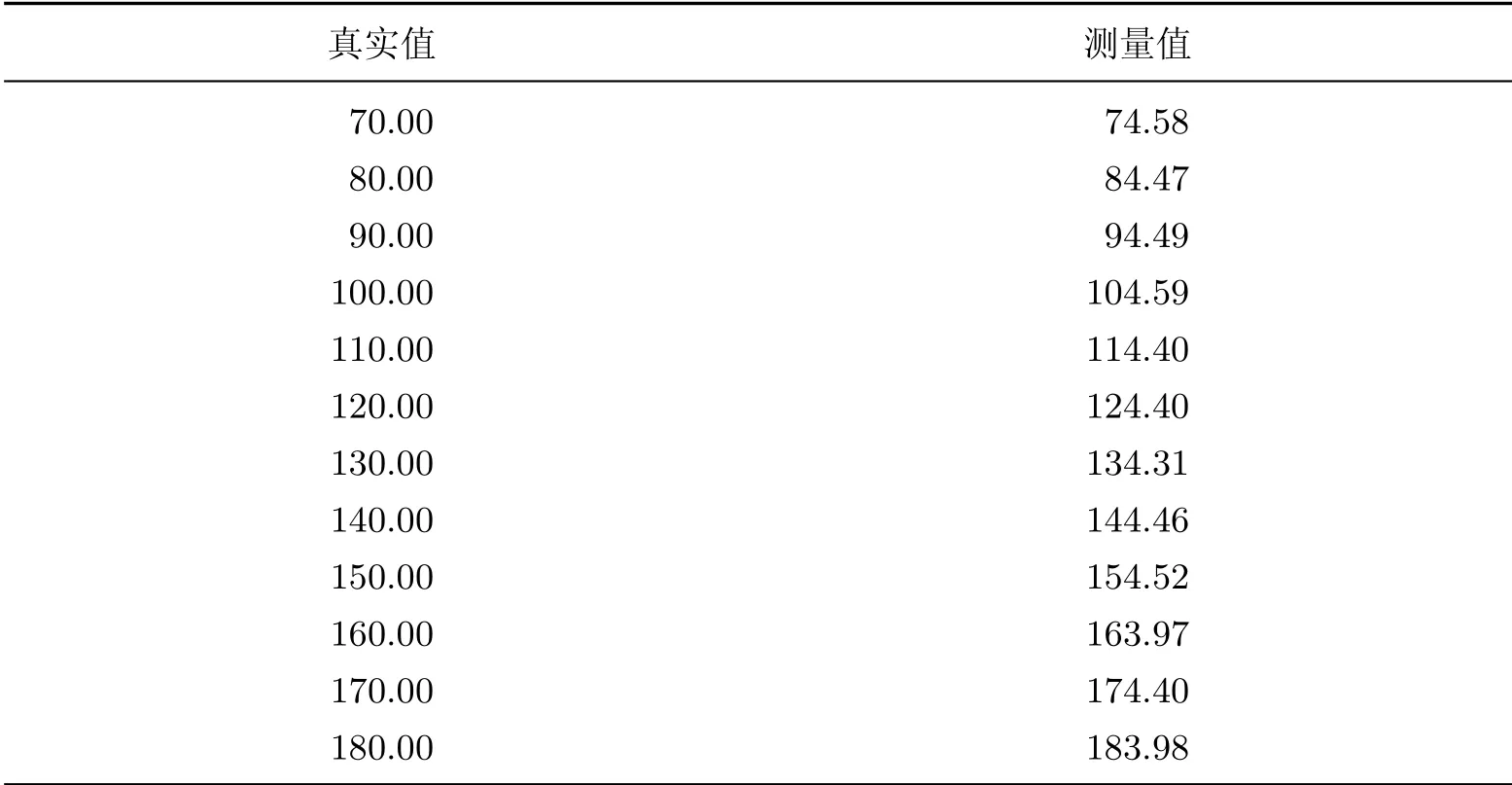
表3 模型参数精度的验证温度采集数据Table 3 Verify temperature acquisition data for model parameter accuracy °C

表4 最优个体及最优参数Table 4 Optimal entities and optimal parameters

依据表4中的最优模型参数计算最终测量值,并与真实值进行比较.经计算,平均误差仅为0.13°C,采集精度可达99.89%;与非优化模型参数的平均误差(0.36°C)相比,优化模型参数的数据处理误差降低了63.20%.处理后的测量值与真实值的对比结果如图7所示.

图7 处理后的测量值与真实值之间的对比Fig.7 Comparation between the processed measured value and the true value

由图7可知,优化模型参数处理后的测量值与真实值基本一致,表明本工作所提算法可以有效搜寻最优模型参数,同时基于算法所构建的数据采集系统也具有较高的数据采集精度.

4 结束语

为高精度获取设备的实时工艺数据,本工作在设计数据采集系统结构的基础上,针对实际采集处理参数标定过程中测量值与真实值数据采集时间不同步的问题,以设备显示值为真实值,以线性模型作为数据处理模型构建目标函数,采用Jaya优化算法搜索最优模型参数;以设备温度数据采集为例,构建实验平台并进行实验验证.实验结果表明,采用优化后的模型参数进行数据采集,平均误差仅为0.13°C,采集精度可达99.89%,相比于未经寻优的模型参数,平均误差可降低63.20%.上述结果表明,本工作提出的数据处理参数标定算法是有效的,所构建的数据采集系统具有较高的数据采集精度.