超空泡鱼雷命中概率解析方法

谢超,周景军,万亚民,宋书龙,王梦豪

(中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

超空泡鱼雷利用水下空泡减阻技术,采用火箭发动机作为主要动力,具备极高的航速和强大的破坏力,是一种新型超高速水下武器。苏联研制的“暴风雪”鱼雷是世界上第1 条成型的超空泡鱼雷,其直径534.4 mm,长度8.2 m,质量2.7 t,航速200 kn,可装载核弹头[1]。

超空泡鱼雷具有特殊的结构布局,其头部锥段部分装配有空化器以辅助空泡形成,极大提高了头部集成声呐基阵的设计难度;同时其航行过程中巨大的自噪声将会降低信噪比,所以目前超空泡鱼雷主要采用直航攻击方式。

潜射直航鱼雷一般采用“提前角”的方式进行攻击,即鱼雷发射航向提前于当前目标方位的某一角度[2-3]。在直航鱼雷的攻击过程中,由于缺少自导系统的修正,所以其命中条件较为苛刻,需要在射击前准确获得目标方位信息、目标航速航向信息等战场态势,在射击时保证足够发射精度,航行过程中还需稳定控制航速、航向,所以直航鱼雷受多种误差因素影响[4]。因此,超空泡鱼雷高航速的特点要想在实战中获得极大的发挥,就需明确各项误差对超空泡鱼雷命中效果的影响。

命中概率是评估命中效果的关键指标,武器的命中概率是指在特定态势下,武器命中目标的可能性,是确定作战方案的重要参考[5]。影响命中概率的因素主要有目标性质、机动能力、对抗方式、武器类型及武器攻击方式等,但从根本上讲,命中概率与误差息息相关。造成武器命中目标不确定性的误差大致可分为两类,一是目标误差,包括目标运动的不确定度以及探测设备对目标的类型、几何尺寸、机动能力等性质的探测误差,这关系到武器系统能否准确得到理论命中点;二是武器的射击误差,由于武器本身的设计、装配误差以及环境中不可预测的误差,导致武器在发射后无法沿预定轨迹到达理论命中点。实际上,还应包括如火控系统解算目标运动要素时的计算误差,以及射击方式缺陷产生的误差等,这些误差均可归到上述两类中。

目前计算鱼雷的命中概率大多以统计法[6-10]为主,即在同一态势条件下仿真上万次,统计命中次数的占比,作为当前态势的命中概率。该方法计算过程简单,但计算量大,同时无法揭示各误差项的灵敏度。利用解析方法来计算命中概率的相关研究很多[3,6,11-16],基本计算思路是先确定鱼雷命中目标的判断指标,再将误差源的方差转换为该指标的方差,由于各误差均服从均值为零的正态分布,所以将指标的概率密度函数在某区间内积分即可。

目前解析方法仍存在一些问题。首先是鱼雷命中目标的判断指标,出于工程实践角度的考虑,该指标多为鱼雷落点在目标航向方向上的投影散布,即只考虑了目标长度,而忽略了宽度,如文献[15]所述方法。尽管这一做法对射击精度要求更为严格,但与实际命中概率具有一定差异,尤其体现在目标小舷角和大舷角处,这容易造成攻击平台的误判,错过最佳射击态势,对于瞬息万变的战场环境来说,这种方法显然不可取。其次是对鱼雷理论瞄点和实际落点存在误解[3],如在计算直航鱼雷的提前角或自导鱼雷的一次转角时,攻击平台应以鱼雷标称速度作为参数进行求解,即提前角误差只与探测值有关,而与鱼雷实际航速误差无关。在发射鱼雷时,再考虑鱼雷本身误差对实际射击角度的影响。最后是多数研究没有考虑目标的运动误差[12]。

针对以上问题,文中首先从理论上分析了计算命中概率的一般过程,提出了目标运动要素条件探测误差,将目标散布与攻击方的探测误差相结合,有效地避免了目标二维散布带来的计算困难问题;其次建立了鱼雷脱靶量模型,明确了鱼雷距离目标最近时呈一维散布规律;然后利用协方差转换方法,将各误差源方差转换为鱼雷脱靶量方差。同时针对目标舰艇实际水线面形状,建立了目标命中范围模型,针对不同目标型号,只需输入相应的水线半宽值即可。最后进行统计方法和解析方法的对比试验,证明了解析算法的准确性,并分析了各个误差源的灵敏度受初始雷目距离、初始目标舷角和雷目速度比影响的变化规律,提出短距离、小舷角态势可适当降低鱼雷脱靶量散布误差,对提高命中概率具有一定参考。

1 命中概率分析

水面目标以一定的方向、速度航行时,受误差影响,航速航向偏离理论值。在某一时刻,目标依概率分布在某个区域内。攻击方在发射鱼雷前对目标进行探测,由于探测设备的误差,使得获得目标当前时刻的速度、航向不准确。攻击方在探测值的基础上,计算鱼雷的发射航向。由于设计和装配精度等问题,鱼雷的实际发射航向偏离理论航向,导致鱼雷的落点依概率分布在某区域内。最终当鱼雷和目标的位置关系满足某命中要求时,说明鱼雷命中目标。

在上述过程中,提取出影响鱼雷命中概率的关键变量:目标散布、鱼雷射击方式、鱼雷散布和命中条件,故命中概率可表示为

如果命中条件采用区域命中法,即若鱼雷与目标的最终落点在某限定区域内,则认为命中,如果在区域外,则没有命中。那么,命中概率为

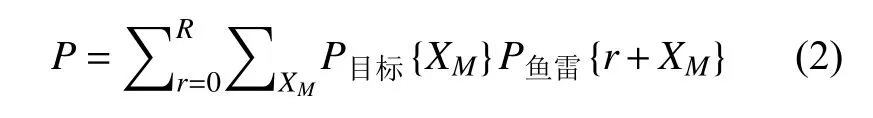
式中:r为鱼雷与目标的最终落点距离;R为命中区域;XM为目标落点;XT为鱼雷落点;P{X}表示落点在X的概率。

通过前文对整个攻击过程的叙述,可以知道鱼雷散布受2 个因素影响,一是火控计算机计算鱼雷理论瞄点的准确度,二是鱼雷射击时产生的误差。根据卷积公式,有

将式(3)代入到式(2)中,有

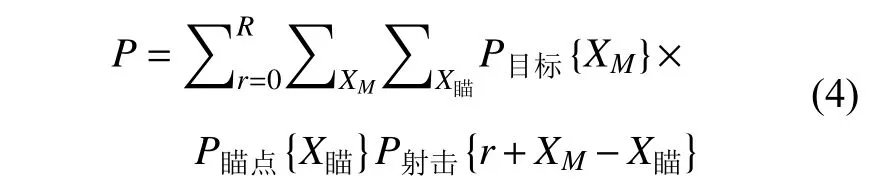
若定义鱼雷条件落点X条件=XM-X瞄,则有

将式(5)代入到式(4)中,则命中概率为

式(6)表明,若将目标舰艇航行误差叠加到攻击平台对目标运动要素的探测误差上,构成目标运动要素条件探测误差,进而形成鱼雷条件落点,则命中概率与目标散布无关。

目标舰艇的航行误差与攻击平台的探测误差相互独立,所以目标运动要素条件探测误差为

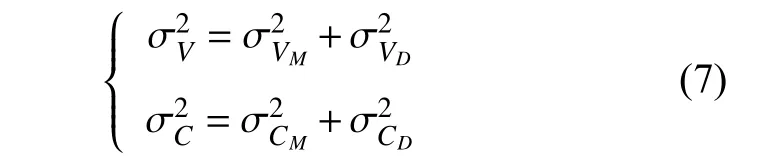
2 攻击过程数学模型

2.1 鱼雷“提前角”攻击模型

鱼雷和目标舰艇初始态势如图1 所示。图中,XOY为大地坐标系,X指向正北且为参考方向,Y指向正东,角度以顺时针方向为正;TM为视线,指当前时刻鱼雷到目标的方向;q为视线角;r为雷目距离;η为目标舷角,该角度以目标舰艇为参考,描述来袭鱼雷的初始方位;CT为鱼雷航向;VT为鱼雷速度;CM为目标航向;VM为目标速度。

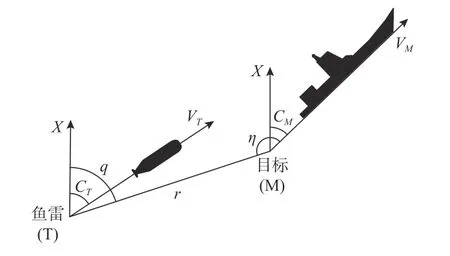
图1 鱼雷攻击目标舰艇示意图Fig.1 Diagram of torpedo attacking target vessel

目标舷角可由初始视线角和目标速度确定,规定鱼雷在目标左侧为负、右侧为正,则有

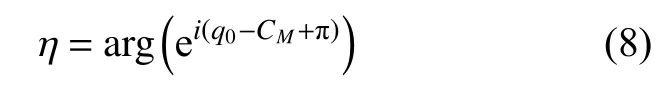
式中,arg(·)为 复数在 [-π,π)上的幅角主值。攻击平台根据初始态势,以提前初始视线角某一确定角度 φ发射鱼雷。由雷目初始位置和理论命中点构成的相遇三角形中,应用正弦定理可得

2.2 鱼雷脱靶量

根据图1 建立相对运动方程组

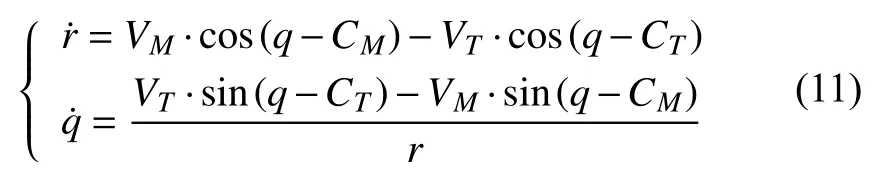
由上式可得

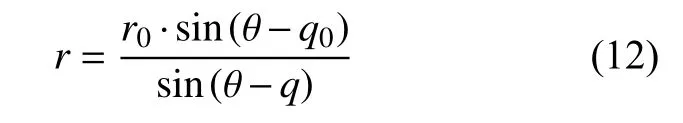
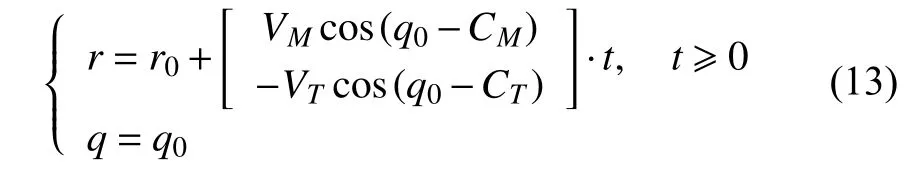
实际攻击过程中,存在误差影响,令式(11)上式为0,可求得相对距离最小值,即脱靶量为

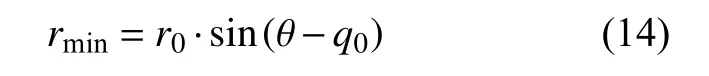
规定鱼雷在目标左舷时脱靶量为负,右舷为正。

3 命中概率模型

3.1 协方差转换法

假设随机向量X=(x1,x2,···,xn)T、Y=(y1,y2,···,yn)T存在如下函数关系

其中G(·)=(g1(·),g2(·),···,gn(·))T。假设X0为真值,X为存在误差的实际值,即X=X0+ΔX,则Y的误差为 ΔY=G(X)-G(X0),将其在真值X0处展开并忽略高阶误差,则有

根据中心极限定理,随机误差服从0 均值的正态分布,由式(16)可知,ΔY与ΔX呈近似线性关系,所以由误差ΔX引起的ΔY近似服从0 均值的n维正态分布,若令,其协方差矩阵为

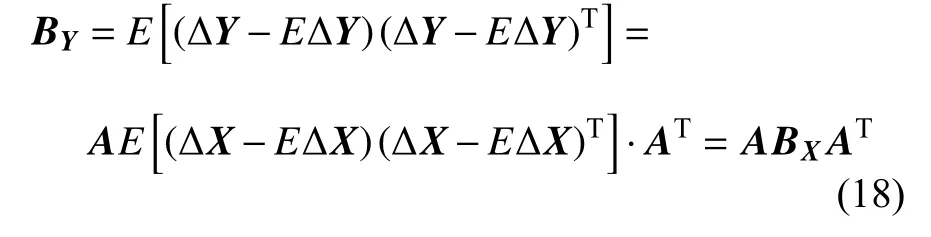
式(18)表明,只要明确函数关系,即可将误差源的误差转换为所需变量的误差。

3.2 鱼雷速度航向协方差

结合式(8)～(10)可知,鱼雷航向是初始视线角、目标航速、航向探测值的函数,假设这些变量相互独立,则定义其协方差矩阵为

特别注意的是,根据式(9)可知,鱼雷航向与其航速有关,但攻击平台在计算鱼雷发射方向时,通常代入标称航速,所以不考虑其误差对鱼雷航向的影响。

根据式(16)可计算出鱼雷理论航向方差为

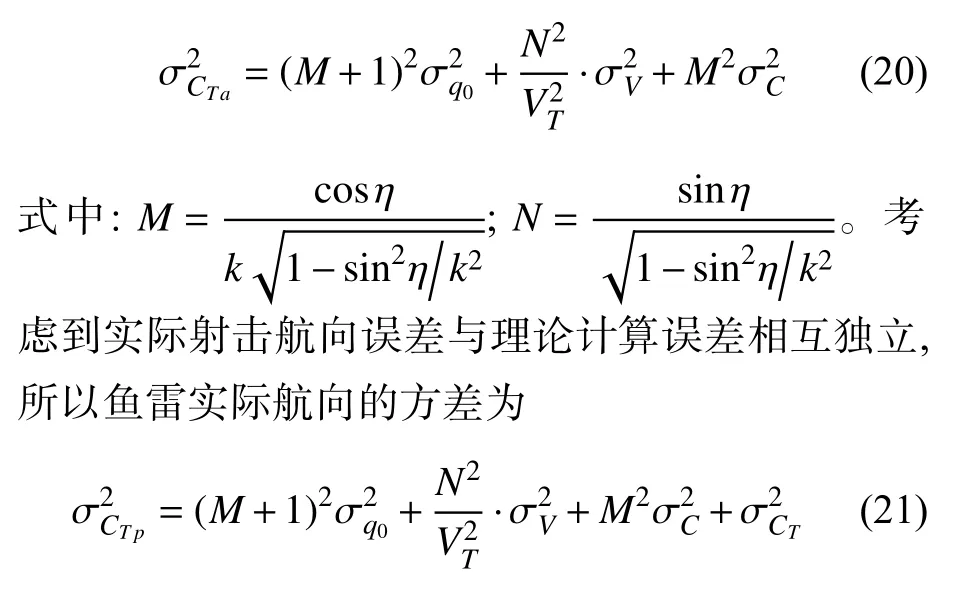
所以鱼雷航速航向协方差矩阵为

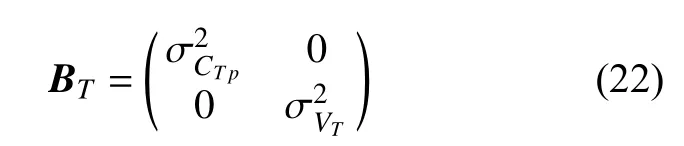
3.3 鱼雷脱靶量协方差

雷目相对速度方向

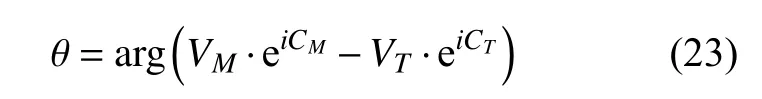
则由鱼雷航速航向误差到雷目相对速度方向误差的系数矩阵为

根据式(14)鱼雷脱靶量方差与相对速度方差关系为

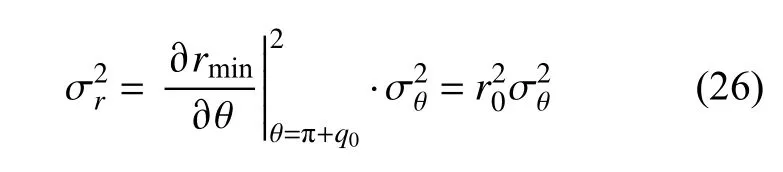
最终可得鱼雷脱靶量方差

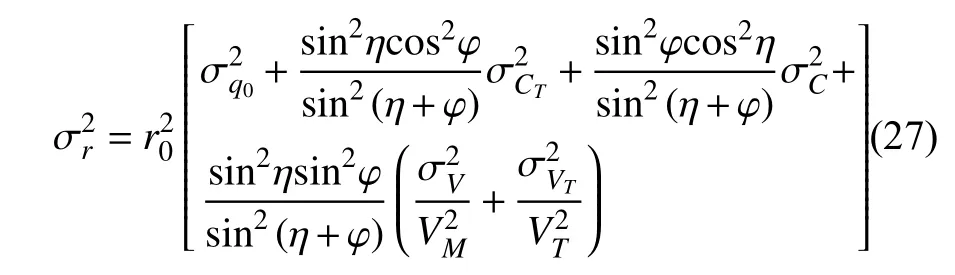
3.4 目标命中范围

若采用区域命中法,则认为当鱼雷落点与目标落点在某区域内,鱼雷命中目标,该区域一般为目标舰艇水线面。

在实际射击中,鱼雷相对目标的无数个可能的直线轨迹中,只有与目标水线面相切或相割的轨迹才是命中轨迹,其中相切轨迹是所有命中轨迹的边界。

由前文分析可知,鱼雷脱靶量是瞄准中心到鱼雷相对目标轨迹线的有向距离,那么相切轨迹对应的脱靶量即为可命中脱靶量范围的边界。如图2 所示,ll为目标左舷侧相切轨迹;lr为目标右舷侧相切轨迹;rl为目标左舷侧可命中脱靶量边界;rr为目标右舷侧可命中脱靶量边界。

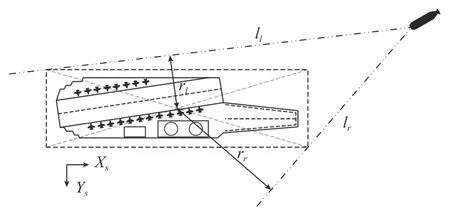
图2 目标命中区域示意图Fig.2 Diagram of target hitting area

以目标舰艇水线面中心为原点,船长方向为Xs轴,船右舷为Ys轴建立目标坐标系。令鱼雷射击瞄准点为(xaim,yaim),目标舰艇水线面半宽曲线为f,船艏坐标为H(xH,±f(xH)),船艉坐标为S(xS,±f(xS)),鱼雷初始位置T点坐标为(xT,yT)=(r0cosη,r0sinη),则相切轨迹方程为

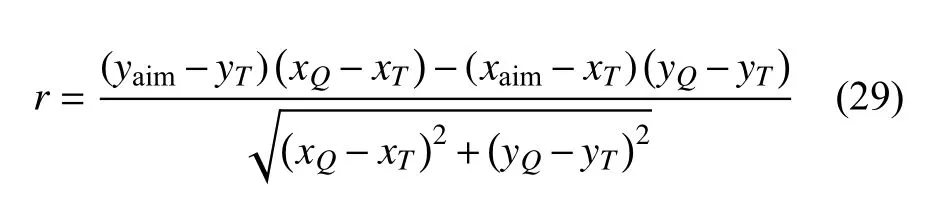
所以可命中的脱靶量范围为

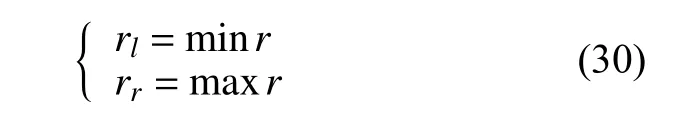
3.5 命中概率计算

由于鱼雷脱靶量服从均值为零的正态分布,且方差与积分区间已由前文给出,所以命中概率为

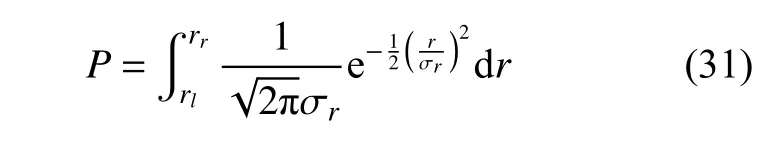
下文将针对这一公式的精确性进行仿真试验研究。

4 统计验证模型

统计模型的计算流程如下。

1) 确定输入变量有:初始视线角q0;初始雷目距离r0;目标舰艇速度VM;目标舰艇航向CM;目标舰艇水线半宽值f;鱼雷速度VT;统计次数N=10000。

2) 探测变量为

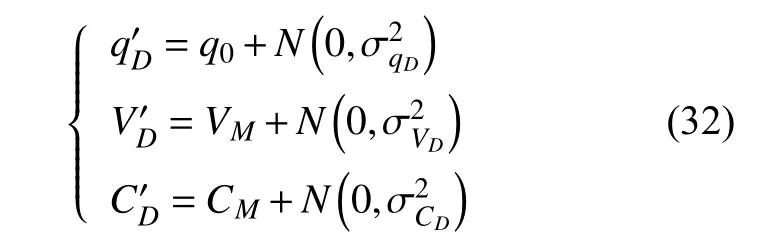
3) 对式(8)～(10)中初始视线角、目标航速和目标航向代入探测值,鱼雷航速代入标称值,可计算出鱼雷理论发射航向CT。

4) 考虑射击诸元误差,计算鱼雷实际发射航向

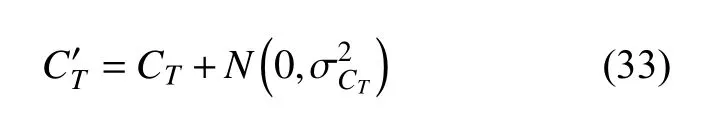
5) 计算鱼雷和目标舰艇得实际航速、航向

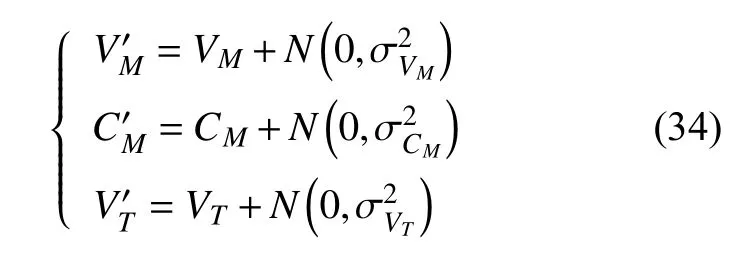
6) 求某时刻地面坐标系下雷目相对位置

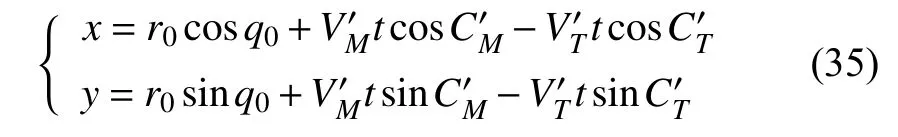
7) 求某时刻目标坐标系下雷目相对位置

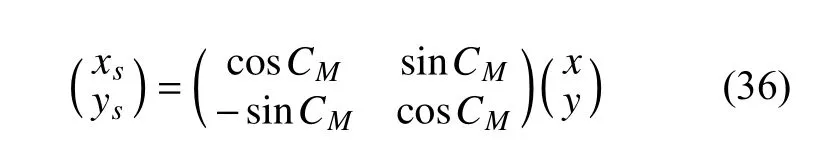
8) 令时间t=0:0.01:查找是否有如下位置关系的时刻

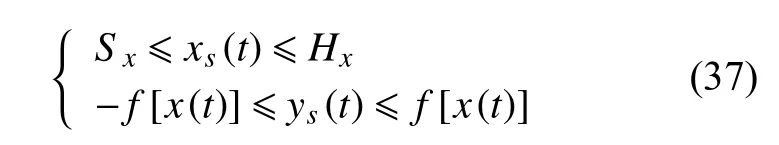
若存在,则表示本次攻击命中目标,令n=n+1。

9) 返回步骤2),直到试验次数达到N,则当前态势命中概率为

5 仿真试验

鱼雷和目标的基本仿真参数设置见表1。目标选用某型散货船,其水线半宽值见表2,水线面如图3 所示。

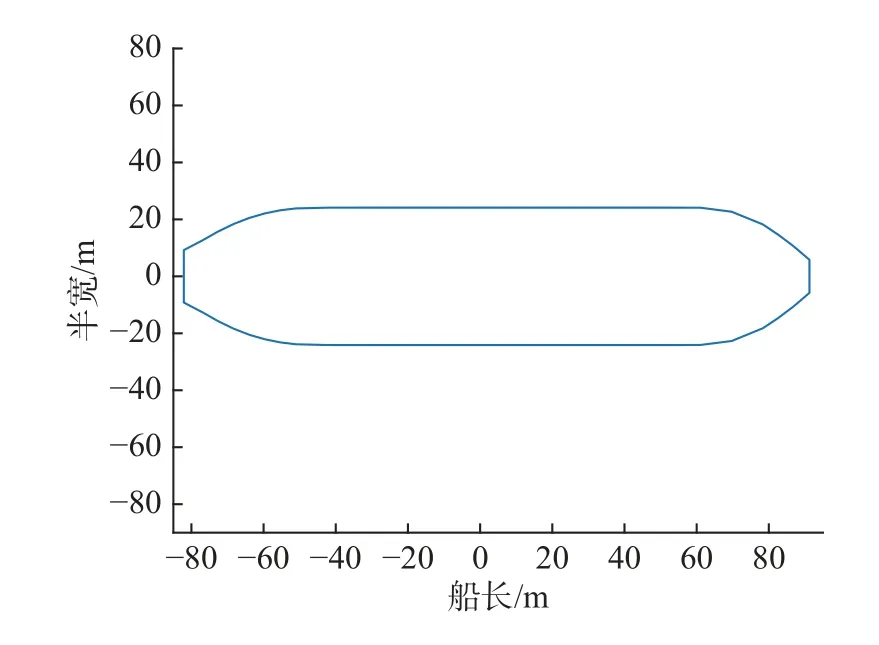
图3 目标船水线面示意图Fig.3 Plot of water plane of target vessel

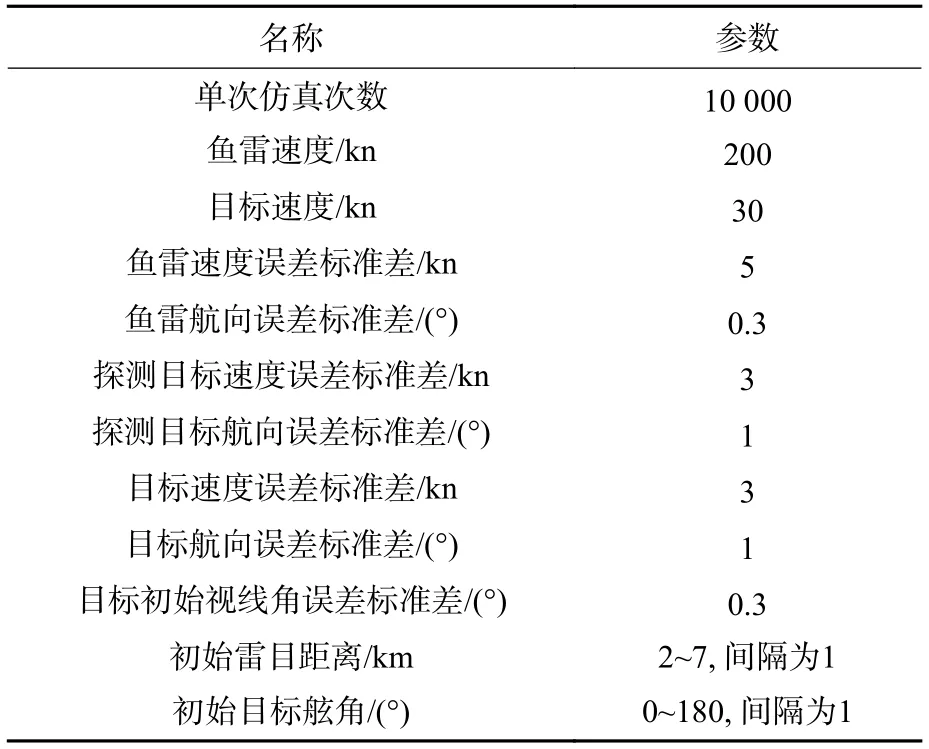
表1 鱼雷及目标仿真参数列表Table 1 List of simulation parameters of the torpedo and the target

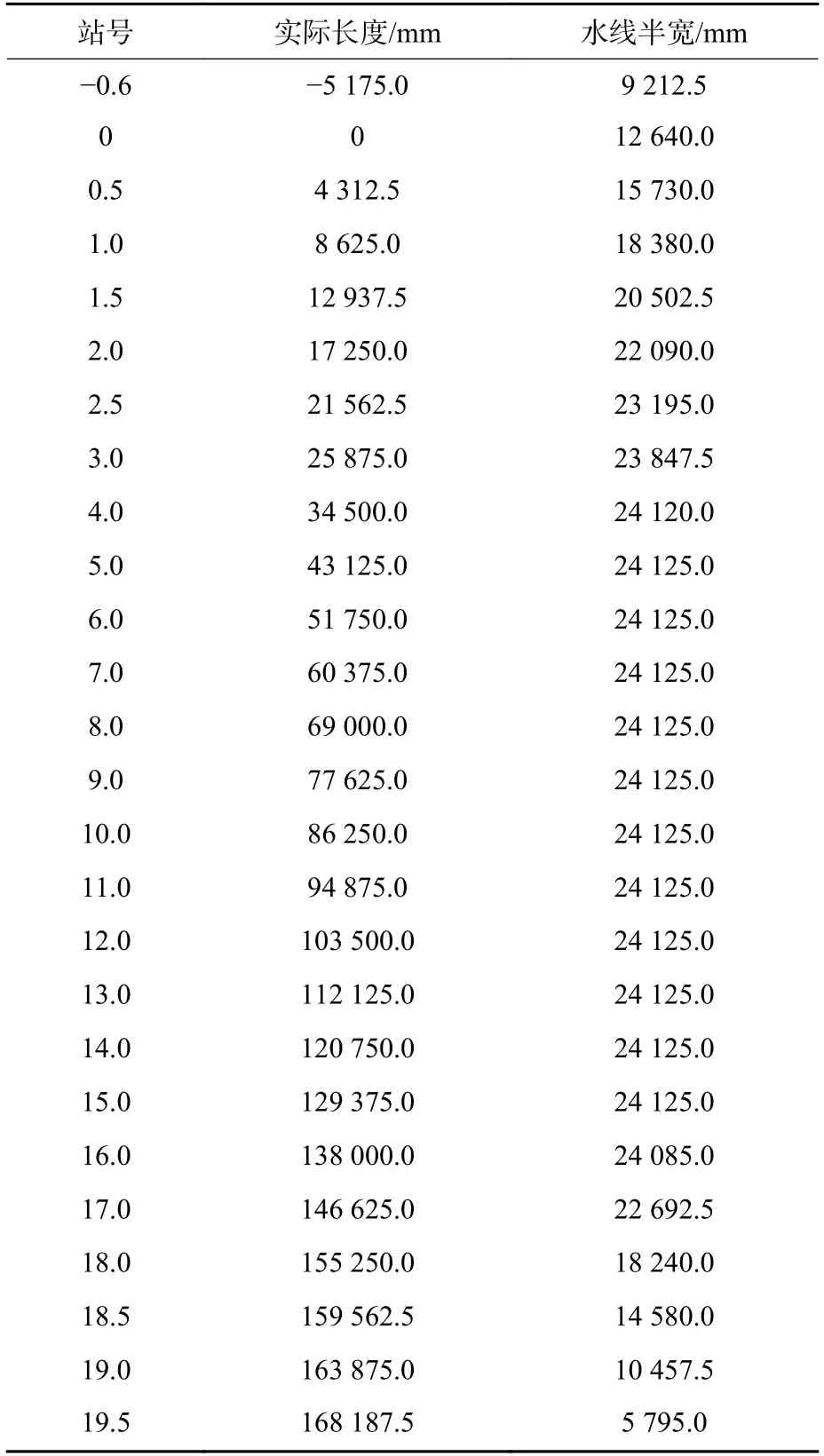
表2 目标船水线半宽值Table 2 Halfbreadth waterline of target vessel

5.1 命中概率

解析法与统计法命中概率曲线如图4 所示。解析模型和统计模型均显示,命中概率随初始雷目距离增大而减少,3 km 以内命中概率基本在70%以上,是较为理想的射击距离。在相同初始距离处,小舷角和大舷角对应更低的命中概率,这是由于这些态势对应的目标命中范围较小。在20°～160°的舷角范围内,命中概率基本呈减小趋势,20°对应同一初始雷目距离下最大的命中概率。

5.2 解析法与统计法偏差范围

对图4 结果中解析概率Pa和统计概率Ps进行如下运算,以获得2 种方法的相对偏差

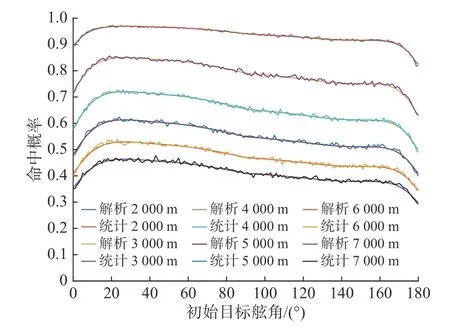
图4 命中概率随初始距离和目标舷角变化曲线Fig.4 Curves of hitting probability changing with initial distance and target board angle

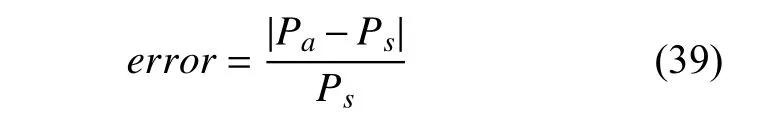
偏差范围及占比见表3。

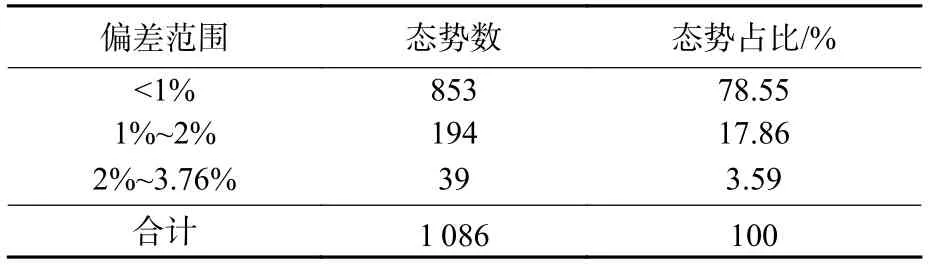
表3 解析法与统计法偏差范围比较Table 3 Contrast of deviation range between analytical method and statistical method

由上表可知,解析法与统计法的最大偏差不超过3.76%,且有96.41%态势的偏差集中在2%以内,验证了解析方法的正确性。

6 误差灵敏度分析

鱼雷命中概率受鱼雷脱靶量散布误差和目标命中范围共同影响,而脱靶量散布误差由脱靶量方差决定。根据式(27)可求得脱靶量方差对射击过程中各种误差变化的敏感程度,令

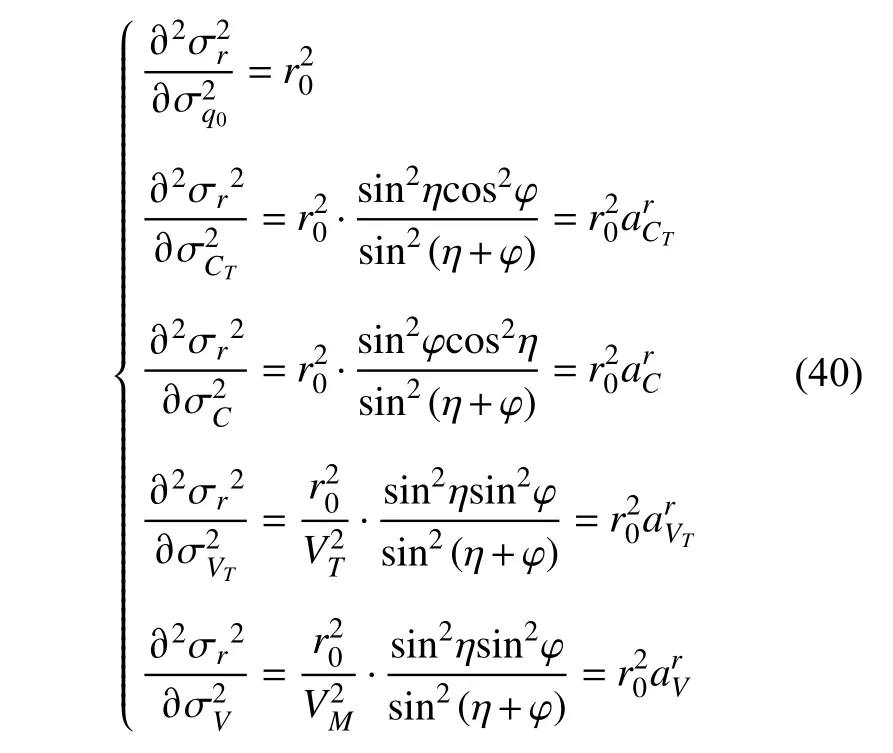
由式(9)和式(40)可知,各误差灵敏度受初始距离、初始目标舷角以及雷目速度影响。初始距离是共同影响因素,初始距离越大,各误差项的灵敏度越大,导致脱靶量的误差增大,从而降低命中概率。

若令目标航速30 kn,计算不同雷目速度比和初始目标舷角对应的来探究二者对灵敏度的影响,结果如图5 所示。

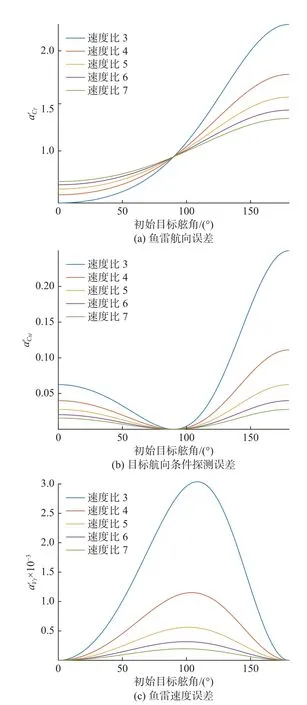
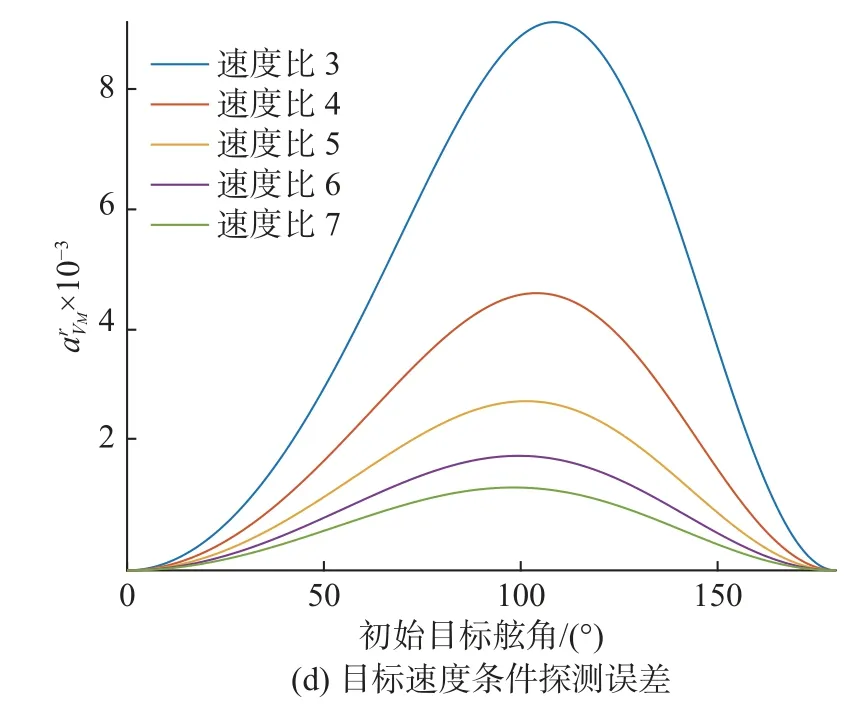
图5 不同速度比下灵敏度随舷角变化图Fig.5 Curves of sensitivity changing with board angle at different velocity ratios

总体来看,在相同误差源大小的情况下,高速鱼雷造成的鱼雷脱靶量误差更小,只有鱼雷航向误差在小于 90°舷角攻击时,低航速却对应更低的灵敏度。

鱼雷脱靶量误差的主要影响因素为鱼雷航向误差和初始视线角探测误差。根据式(40),鱼雷航向误差的系数为,由图5可知在0°～90°小于1,而在 90°～180°大于1;初始视线角的系数始终为,所以小于 90°舷角时,初始视线角误差影响更大;大于 90°舷角时,鱼雷航向误差影响更大,其次影响程度依次为目标航向条件探测误差、目标航速条件探测误差以及鱼雷航速误差。

鱼雷航向误差和目标航向条件探测误差在小于 90°舷角时,灵敏度变化范围较小;而在大舷角范围内,随着舷角增大,灵敏度增长更快,相应的脱靶量误差也会更大。鱼雷航速误差和目标航速条件探测误差的灵敏度峰值在 [100°,110°]舷角范围内,在大小舷角处灵敏度趋于0,并且根据式(38),二者灵敏度受绝对速度大小影响,所以对鱼雷脱靶量误差的贡献度相对较小。

综合以上分析,鱼雷应在短距离、小舷角范围内攻击目标,以减小鱼雷脱靶量散布误差。同时还应综合考虑目标命中范围,最终提高命中概率。

7 结束语

文中主要建立了超空泡鱼雷命中概率解析模型,该模型用一元积分描述,其中考虑了目标散布误差、攻击平台探测误差、鱼雷航行误差以及目标水线面区域。解析模型有效降低了计算量,为后续鱼雷控制参数实时优化提供参考。通过与统计模型的对比仿真试验,验证了解析模型的准确性。文中还进行了误差灵敏度分析,明确了影响鱼雷脱靶量散布的主要原因,对提高命中概率所需的相关指标精度要求给予一定参考。

由命中概率结果可知,相较于常规声自导鱼雷,超空泡鱼雷单雷打击的战术优势并不明显,所以未来将进一步评估在多雷齐射的战术方案下超空泡鱼雷各态势的命中概率。