基于瞬时特征参数和功率谱熵的联合调制识别

谢爱平,张雨生,刘 莹,何梓昂,高 锐

(1.中国电子科技集团第二十九研究所 电磁频谱研究中心,四川 成都 610036;2.扬州大学 信息工程学院,江苏 扬州 225127)

随着通信技术时代的快速发展，人们对信息传输的要求也越来越高，这也使得通信信号的调制方式逐渐多样化，通信系统之间的信号快速互通已成为待解决的难题。信号调制识别(Modulation Recognition，MR)是解决这个难题的关键技术。在通信系统中，调制识别[1-3]被广泛应用于军用和民用通信当中。在军事领域，信号调制识别能够分析接收到的目标信号，推动对信号解调等后续处理过程，从而获取所需的情报信息。该技术还能通过识别出的信号信息，选取参数对敌方信号进行干扰，削弱及破坏敌方电子设备的使用效能。在民用领域中，调制识别能够帮助对频谱资源的监管，保障合法通信能够正常进行，避免出现各项损失。但目前已有调制识别的方法计算复杂，在低信噪比环境下识别率低，甚至无法识别多进制信号，因此对于调制方式的识别问题还需要进行更深入的研究。

在目前的研究中，常用的调制方式大致有3种：基于决策理论的最大似然比(Likelihood-Based，LB)假设检测方法[4-6]、基于深度学习(Deep Learning，DL)的调制识别方法和基于特征参数提取的识别(Feature-based，FB)算法。LB算法是通过在获取信号的似然函数的基础上比较阈值和似然率的关系来进行判决的，可以分为平均似然比检验、广义似然比检验、混合似然比检验等。基于DL的调制识别方法利用深度神经网络的自组织自学习机制，通过网络内部的非线性函数来实现特征提取，并结合相应分类器完成对信号的识别。基于特征参数的调制识别方法可选取能够表征信号调制方式的分类特征，根据不同类别调制信号特征参数之间的差别来制定符合要求的分类规则，并对识别方式进行判决。在以上方法中，FB算法的调制识别方法的计算量较小，设置合适的门限较容易，并且可达到接近最优的分类性能，因此被广泛应用与研究。其具体识别过程主要为：

步骤1将接收的高频信号进行下变频等预处理；

步骤2对处理后的信号进行提取并计算其特征参数值；

步骤3根据提取到的特征参数值，利用不同的分类方式和分类器进行调制分类判决。

早在上世纪90年代，文献[7～11]就提出了通信系统的基于瞬时特征参数的调制识别方法。该方法通过将信号的瞬时信息(幅度、频率、相位)进行零中心、归一化处理，得到改进的瞬时特征值。改进后的瞬时特征值能够有效提高在信噪比大于10 dB时调制信号识别的准确性。不仅如此，在信号调制识别过程中，信息熵也是衡量信号复杂度的一个重要指标，信号调制类型不同，其信息熵也各有差异。文献[12]提出将功率谱熵、小波能熵值、奇异谱熵等六维熵特征值作特征参数用于信号分类，实现了对多个信号的有效分类识别。

以上这些特征参数算法虽能有效对数量较少的目标信号进行精准识别，但它们在数字调制信号的全面识别方面效果不佳，尤其是在低信噪比下对高阶信号的识别效果有待提高。考虑到这些问题，本文对基于特征参数提取的识别方法做出改进，提出了基于改进特征参数与信号功率谱熵联合的调制识别方法。该算法提取信号的6个瞬时特征参数(MA1、MA2、MP1、MP2、MF1和Hs)作为特征向量，并用决策树分类方法对常用的9种数字调制信号{ASK、4ASK、2FSK、4FSK、8FSK、BPSK、QPSK、8PSK、16QAM}进行分类。

1 经典算法的性能分析

1.1 基于特征参数提取的调制识别过程

基于特征参数的识别方法首先选取能够表征调制信号特性的参数，然后根据各调制信号特征参数的差异对信号进行识别判决。具体过程如图1所示。

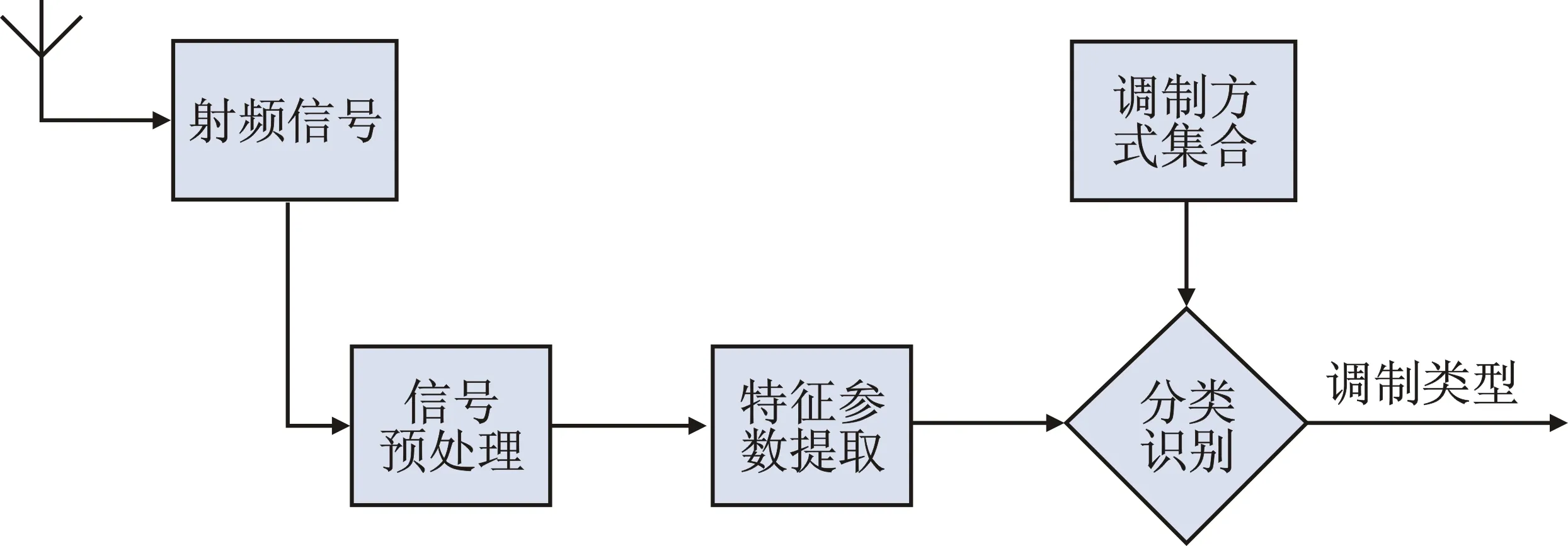
图1 基于特征参数提取的调制识别过程

1.2 已有方法及其不足

数字信号调制是现代通信的重要方法，其过程一般都是由幅度、频率和相位中的一个或多个参数进行，因此瞬时幅度、瞬时相位及瞬时频率构成了数字调制信号的瞬时特征信息[13-14]。

目前常见的瞬时特征参数提取法分为两种，即传统瞬时特征法和改进后的瞬时特征法。这两种方法的区别在于所提取的特征参数是不相同的，这就导致识别的信号种类以及识别性能也不相同。接下来将介绍这两种方法各自的参数提取及方法存在的问题与不足。

1.2.1 传统瞬时特征法及其存在的问题

传统的瞬时特征值方法主要是通过提取γmax、σap、σaa、σdp、σaf这5种瞬时特征值[15-17]来对2ASK、4ASK、BPSK、QPSK、2FSK、4FSK这6种调制信号进行调制方法的识别。

瞬时幅度谱峰值γmax的计算式为

γmax=max|(FFT[a(i)/E(a(i))-1])2/Ns|

(1)

式中，a(i)为信号的瞬时幅度；Ns为信号的采样点数。

瞬时幅度绝对值标准差σaa为

(2)

式中，c为采样信号中非弱信号的个数，为判断信号段是否为非弱信号的门限。

瞬时相位绝对值标准差σap为

(3)

式中，φNL(i)为非线性瞬时相位。

瞬时相位标准差σdp为

(4)

瞬时频率绝对值标准差σaf为

(5)

式中，fNL(i)为的非线性瞬时相位。

以上5个瞬时特征值能实现对6种数字调制信号的识别：(1)恒幅信号的γmax基本为0，因此能实现MASK、MPSK、MFSK的类间识别；(2)σaa能够实现MASK的类内识别；(3)σap可以实现MPSK的类内识别；(4)MFSK不含相位调制，所以σap为0，而MPSK的σdp值大于0，因此σdp能够实现MFSK与MPSK的类间识别；(5)σaf可以实现对MFSK的类内识别。从传统的瞬时特征方法的分析可以发现，基于传统瞬时特征值的方法能够较好地完成信号的类间识别，但是在低信噪比阶段、类内识别和高阶调制信号的识别性能表现不佳，由此也出现了一种改进的基于瞬时特征参数的调制识别方法。

1.2.2 改进的瞬时特征参数法及其存在的问题

改进的瞬时特征法选取改进后的瞬时特征值[18]作为特征参数，利用MA1、MA2、MP1、MP2、MF1、MF2、MF3这7个参数来实现对ASK、4ASK、2FSK、4FSK、8FSK、BPSK、QPSK、8PSK、16QAM这9种数字调制信号的识别。

瞬时幅度绝对值的均值MA1为

(6)

式中，n为采样点数；a(i)为信号的瞬时幅度，由信号经过希尔伯特变换后计算得到。

递归瞬时幅度绝对值的均值MA2为

(7)

式中，MA1为式(6)中的瞬时幅度绝对值的均值。

瞬时频率绝对值的均值MF1的计算式为

(8)

式中，f(i)为瞬时频率。

递归瞬时频率的绝对值均值MF2的计算式为

(9)

递归瞬时频率的绝对值均值MF3为

(10)

式中，f1(i)=|f(i)|/|E(f(i))|-1。

瞬时相位绝对值的均值MP1为

(11)

式中，φ(i)为瞬时相位。

递归瞬时相位绝对值的均值MP2的计算式为

(12)

式中，φ1(i)=φ(i)/E(φ(i))-1，而φ(i)为瞬时相位。

以上7个特征参数基本能够实现常见数字调制信号的识别。MA1可以实现对16QAM的识别和 MASK、MFSK和MPSK这3类调制方式的类间识别。MA2可以实现MASK的类内识别。MF1可以实现MFSK和MPSK的类间识别。MP1和MP2可以实现对MPSK类内分类识别，然而MF2、MF3这个两个特征参数在MFSK信号的类内分离特性效果不佳，因此还需要寻找其他的特征参数来解决MFSK的类内识别问题。改进后的方法与传统方法相比，识别的信号种类有所增加，但是低信噪比时的识别性能和高阶信号的识别方面仍然表现不佳，因此还需要寻找其他方法来改善在低信噪比下的识别性能。

2 基于瞬时特征参数和功率谱熵的联合调制识别

针对传统方法和改进的瞬时特征参数法存在识别信号种类少、低信噪比时识别性能不佳、无法识别高阶调制信号等问题，本节提出了一种基于瞬时特征参数与功率谱熵联合的调制识别方法。该方法在改进的特征参数的基础上，引入功率谱熵的特征来解决MF2和MF3这两个特征参数在MFSK类内调制识别不佳的问题。

2.1 熵的理论基础

“熵”的概念最早出现在热力学的应用当中，目前已经广泛的应用于很多领域。熵在通信信号处理中通常用于衡量信息量，熵值越大，信息不确定度也越大，其中主要有香农熵和香农指数熵[19]。

香农熵的定义为

(13)

香农指数熵为

(14)

式中，{xi}是服从随机过程的事件；P(xi)为每个事件xi发生的概率，∑P(xi)=1 ,i=1,…,n。

从指数熵的表达式可知，P(xi)是取值范围为[0,1]，则H(X)的值域为[1,e]，当且仅当每个事件发生的概率P(xi)相同时，熵H(X)的值最大。功率谱指数熵的理论值范围为[1,e]，所以门限也应在这个范围内选取，范围太小也给门限的选择带来困难。同理，功率谱香农熵的特征参数理论值没有这样的约束，在功率谱熵特征值的提取时，可以在较大范围内选择合适的门限值，因此本文选择的是功率谱香农熵。

2.2 功率谱熵特征提取

最常见的功率谱的计算方法为根据周期图法[20]计算信号s(n)的功率谱。若信号s(n)的采样长度为n，对其进行离散傅里叶变换后取绝对值再求其平方的均值即可得到功率谱，具体表达式为

(15)

根据熵的定义可得信号s(n)的功率谱熵Hs为式(16)。

(16)

2.3 基于决策树的识别过程

在识别分类方法上，本文采用基于决策树分类器对数字信号进行特征参数提取的调制识别过程。

待识别的信号的集合为{ASK、4ASK、2FSK、4FSK、8FSK、BPSK、QPSK、8PSK、16QAM}这9种调制信号。用于识别的特征参数为上文提到的MA1、MA2、MP1、MP2、MF1、Hs。

基于瞬时特征值和功率谱熵的联合调制识别方法的步骤为：首先计算出各个调制信号的6个特征参数值；然后为每个特征参数设置合适的门限值，将各个调制信号分类。由于MA1能直接识别出16QAM，所以可以设置两个MA1值的门限。同理，Hs可以有效地对MFSK信号进行类内识别，故Hs的门限值也可以设置两个，则设置的门限值为T1～T8。

调制识别的具体过程如下：

(1)将特征参数MA1与判决门限T1比较，如果MA1>T1，则将信号划分为{2ASK、4ASK、16QAM}，否则为{2FSK、4FSK、8FSK、BPSK、QPSK、8PSK}；如果MA1

(2)若信号划分为{2ASK、4ASK}，将特征参数MA2与判决门限T3比较，如果MA2>T3，则将信号判决为4ASK，否则为2ASK；

(3)如果信号划分为{2FSK、4FSK、8FSK、BPSK、QPSK、8PSK}，将特征参数MF1与判决门限T4比较，如果MF1>T4，则将信号判决为MFSK，否则为MPSK；

(4)若信号划分为{2FSK、4FSK、8FSK}，将特征参数Hs与判决门限T5比较，如果Hs>T5，则将信号判决为8FSK，否则为{2FSK、4FSK}，如果Hs>T6，则将信号判决为4FSK，否则为2FSK；

(5)如果信号划分为{BPSK、QPSK、8PSK}，将特征参数MP1与判决门限T7比较，如果MP1>T7，则将待测信号划分为{QPSK、8PSK}，否则为BPSK；接着将特征参数MP2与T8比较，如果MP2>T8，则将待测信号判决为8PSK，否则为QPSK。

图2 基于决策树的调制识别过程

通过以上过程，便可根据提取的6个特征参数，通过决策树的分类方法识别9种数字调制信号。

3 仿真实验及分析

本节按照基于决策树的分类方法的识别过程，利用MATLAB对9种信号进行调制识别的仿真实验。

实验对象：9种数字调制信号{2ASK、4ASK、2FSK、4FSK、8FSK、BPSK、QPSK、8PSK、16QAM}。

实验参数：载波中心频率fc为10 kHz；采样频率fs为80 kHz；码元速率fd为2.5 kHz；MFSK信号的频率间隔Δf为3 kHz；识别信号长度n为1 000；背景噪声为高斯噪声，信噪比范围为0～15 dB；步进为1 dB。对每个调制信号进行10 000次仿真，识别率表示为正确仿真次数和总仿真次数的比值。

3.1 最佳门限确定

最佳门限采用二分法在合适的门限范围内设置门限。通过设置3对不同的Hs门限值来研究不同门限对识别效果的影响，具体设置如表1所示。

表1 不同功率谱熵的门限值

为了找到最佳门限，取MFSK信号在各门限组合下进行仿真实验，并以识别率的平均值表示该门限下的识别性能，具体的不同门限值下识别性能与信噪比的关系如图3所示。

图3 不同Hs门限值的MFSK识别率

由图3对比观察可以发现，在低信噪比时，识别性能并不理想。当信噪比为4～6 dB时，不同门限的识别率影响较大。在门限2的情况下，MFSK信号的识别性能均好于门限1和门限3时的识别性能，于是将暂定门限2为最佳门限值。同理，根据选择不同门限值对比平均识别率的方法也可以找出其余瞬时特征参数的最佳门限值。最后得到所需要的最佳门限值如表2所示。

表2 瞬时特征和功率谱熵的门限值

3.2 调制识别性能与分析

按照上文给出的识别流程以及设置的参数与门限值，对9种待识别信号进行识别性能的仿真。具体仿真结果如图4所示。

图4 9种信号的联合特征参数调制识别的识别率

通过观察图4可以发现，在9种调制信号中，16QAM、2ASK、4ASK具有较好的识别率，并且信号16QAM的识别率一直保持在100%，这是因为它的MA1值稳定，即使是在低信噪比的环境下也不会受影响。特征参数MA2也对2ASK、4ASK具有良好的分类特性，在信噪比达到2 dB时就可以实现MASK信号的类内识别。QPSK信号在低信噪比时识别率较高，在3～4 dB时有下降的现象，这是因为QPSK的特征参数MP2在SNR<4 dB时会缓慢增加到靠近门限值；在信噪比大于4 dB时又会迅速减小，使得识别率会逐渐变好。由于受到噪声和均值运算的影响，BPSK和8PSK信号在低信噪比时识别率并不高，但是当信噪比达到2～3 dB后，信号的识别率会快速提高。BPSK和8PSK信号的识别率在信噪比达到3 dB时已经达到了100%和91%，都拥有良好的识别性能。

MFSK信号的类内识别应用的是功率谱熵的特征，但是其本身受噪声方差的影响较大，所以随着信噪比的增加，功率谱熵值会有所减小。由于决策树的分类方法很难对低信噪比时的功率谱熵值变化做出拟合，因此在信噪比较低时，决策树分类方法不能充分利用MFSK信号的功率谱熵的分离特性。所以当SNR在3～5 dB时，MFSK的类内识别识别率较低，在SNR增加到5～6 dB时，识别率迅速提升，能有效地实现信号识别。

3.3 相关方法的性能对比及分析

通过蒙特卡洛仿真实验，将文中提出的方法同传统方法[9，21]、现有的瞬时特征值识别方法[22]进行了识别性能对比。具体的识别率性能如图5所示。

图5 相关瞬时特征值法的识别率性能对比

由图5可知，传统方法只能识别出6种信号，而改进后的瞬时特征参数法能够识别9种信号，但是平均识别率不如本文所提出的方法。在低信噪比时，传统方法的识别率略优于本文方法，这是因为传统方法识别不了高阶信号，所以识别时特征值不需要顾虑高阶信号。但是随着信噪比的增加，传统方法在MASK和MFSK的类内识别性能不佳，所以识别率仅能达到80%，在信噪比大于12 dB之后，识别率才能达到100%。改进后的瞬时特征参数法对MFSK信号识别不佳，尤其在大动态信噪比范围内平均识别率止步不前，所以在信噪比大于13 dB后能达到100%。因此，本文方法无论是在识别信号的数量还是信号的平均识别率上都要优于另外两种方法。

4 结束语

本文提出了一种基于决策树的瞬时特征参数和功率谱熵联合的数字信号调制识别方法，该方法选择经过运算后的瞬时幅度和瞬时相位的递归均值来实现对幅度和相位调制的识别；引入功率谱熵的特征参数用于MFSK信号的类内识别，来解决瞬时频率特征值对MFSK信号分类性能不佳的问题。采用基于决策树的分类方法进行仿真实验，结合通过实验得到的合适的判决门限，进行2ASK、4ASK、2FSK、4FSK、8FSK、BPSK、QPSK、8PSK、16QAM这9种调制信号的识别。通过实验将本文方法与另外两种方法对比发现，本文基于瞬时特征参数和功率谱熵联合调制识别的方法在识别信号数量上优于传统方法，在平均识别率上优于改进后的瞬时特征参数法，并且对高阶MFSK信号识别性能良好。