中立型随机比例微分方程部分截断Euler-Maruyama数值解的收敛性分析

肖渊琰， 尤苏蓉

(东华大学 理学院， 上海 201620)

随机时滞微分方程(stochastic delay differential equations，SDDEs)被广泛应用于随机系统模型中，SDDEs的演化取决于历史状态。但在实际应用中，很多随机系统不仅依赖于现在和过去的状态，还与时滞项的导数有关，这就催生了中立型随机时滞微分方程(neutral stochastic delay differential equations，NSDDEs)数值解和解析解的研究[1-5]。作为NSDDEs中的一种特殊模型，中立型随机比例微分方程(neutral stochastic pantograph differential equations，NPSDEs)应用于很多实际的领域，如经济、金融、物理、生物、药学等。近年来，NSDDEs和NPSDEs解析解的性质如收敛性、稳定性得到了较为广泛的研究，例如：Liu等[6]研究了高非线性下带Lévy噪声的NPSDEs解的P阶矩指数稳定性；Mao等[7]研究了混杂型NPSDEs的几乎必然稳定；Shen等[8]利用李雅普诺夫函数和M矩阵研究了高非线性条件下NPSDEs的指数稳定性。

在高度非线性条件下很难得到NPSDEs的解析解，这时数值方法的重要性显而易见。经典的Euler-Maruyama法被用于构造满足线性增长条件的随机微分方程数值解，在此基础上，如：Mao[9]提出基于Khasminskii型条件和局部Lipschitz条件的随机微分方程(stochastic differential equations，SDEs)数值解截断EM(euler-maruyama)算法；Guo等[10]提出部分截断EM算法，并证明了方程数值解可在高非线性条件下保证均方指数稳定性和多项式收敛性。随后，部分截断EM算法开始应用于随机微分方程的数值解研究，如：Zhang等[11]利用部分截断EM算法研究一类SDDEs的数值解问题；Zhan等[12]将其应用于随机比例微分方程(stochastic pantograph differential equations，PSDEs)的数值解研究。部分文献对NPSDEs的数值估计进行了研究，如：Zhan等[13]利用向后型Euler方法给出NPSDEs的数值解的几乎必然渐进稳定；程生敏等[14]用相同方法得到了NPSDEs的数值解的指数稳定性。

但是目前鲜有关于高度非线性情况下NPSDEs的显示数值研究，对此，在Khasminskii型条件和压缩映射条件下，利用部分截断EM算法构建高度非线性NPSDEs的数值解，并研究数值解的有界性和收敛性。

1 预备工作

考虑以下中立型随机比例微分方程：

d[x(t)-D(x(qt))]=f(x(t),x(qt))dt+g(x(t),x(qt))dB(t)
x(0)=x0;t>0

(1)

式中：x∈n；f:n×n→n；g:n×n→n×m；D:n→n表示中立项；q∈(0,1)。

假设系数f和g可以被分解为以下形式：

f(x,y)=F1(x,y)+F(x,y)

g(x,y)=G1(x,y)+G(x,y)

式中:F,F1:n×n→n,G,G1:n×n→n×m，分别满足以下假设。

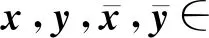
(2)

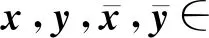
(3)

(4)

当a=1时，以上假设即为Khasminskii条件。

假设1.4(压缩映射条件)存在正常数u∈(0,1)，对所有x,y∈n使得

|D(x)-D(y)|≤u|x-y|且D(0)=0

(5)

由假设1.4推出|D(x)|≤u|x|。

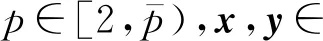
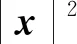
(6)

证明：

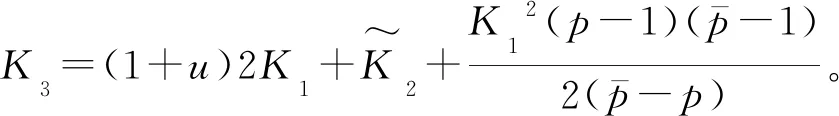
引理1.6[14](存在唯一性)若假设1.1～1.4和引理1.5成立，方程(1)具有唯一解{x(t),t≥0}。

沿用文献[10]提出的部分截断数值解思想，选取一个严格递增的连续函数μ:+→+,使得当r→+∞时有μ(r)→+∞，且

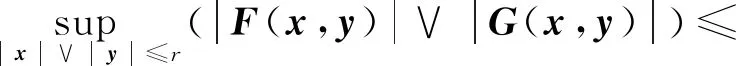
μ(r),∀r≥1

(7)

记μ-1为μ的逆函数，可知μ-1也是严格递增的连续函数，且μ-1:[μ(0)，∞)→+。再选取一个Δ*∈(0,1]，和严格递减函数h:(0,Δ*]→(0,+∞)，使得

(8)

对于给定的步长Δ∈(0,1)，定义一个如式(9)所示的映射πΔ:n→{x∈n:|x|≤μ-1(h(Δ))}。

(9)

当x=0时定义πΔ(x)=0，则定义如下截断函数

(10)

对任意x,y∈n,由式(7)可知

FΔ(x,y)∨GΔ(x,y)≤μ(μ-1(h(Δ)))=h(Δ)

(11)

因此，虽然F,G不满足有界条件，但是FΔ,GΔ一定有界。以下的引理将证明这些截断函数保留了Khasminskii型条件。

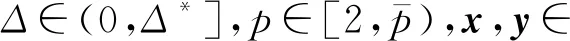
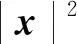
(12)

证明：固定任意的Δ∈(0,Δ*]，由h(Δ*)≥μ(1)可知,μ-1(h(Δ*))≥1，但因为μ-1递增而h递减，所以μ-1(h(Δ))≥1，得到

以下分两种情况证明：

(13)

(1)当x∈n且|x|∨|y|≤μ-1(h(Δ))时，根据假设1.3可知

(2)当x∈n且|x|∨|y|>μ-1(h(Δ))时，对根据假设1.3可知

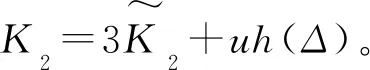
因此

现定义方程(1)的部分截断EM算法如下[10]：

(1)定义：

(14)

其中ΔBk=B((k+1)Δ)-B(kΔ)，而fΔ(Xk,X[qk])=F1(Xk,X[qk])+FΔ(Xk,X[qk])，gΔ(Xk,X[qk])=G1(Xk,X[qk])+GΔ(Xk,X[qk])。

(2)定义离散过程：

(15)

(3)定义连续时间的近似解：

(16)

因此可以看出xΔ(t)在区间[0,+∞)上满足

2 收敛性结果

引理2.1令p>2,记z(t)=x(t)-D(x(qt))，在假设1.1～1.4和引理1.5成立的条件下，对任意T>0，存在C>0(依赖于p,T)，方程(1)的唯一全局解{x(t),t≥0}满足

(17)

如果定义停时τR=inf{t≥0,|x(t)|∨|z(t)|≥R}，则有

(18)

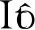
(19)

而

(20)

因此有

(21)

再根据z(t)的定义和不等式(a+b)p≤(1+ξ)p-1(ap+ξ1-pbp),∀a,b≥0,p>1,ξ>0，可得

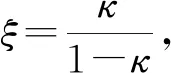
(22)

代入式(21)得到

(23)

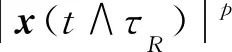
引理2.2若假设1.1～1.4和引理1.7成立，存在C>0(依赖于p,T，但独立于Δ)使得

(24)

且对任意实数R>|x(0)|以及Δ∈(0,Δ*]，定义停时ρΔ,R=inf{t≥0,|xΔ(t)|∨|yΔ(t)|≥R}，成立

(25)

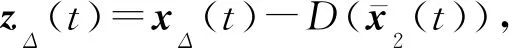
分别对上式右侧3个积分进行分析可得

(26)

(27)

(28)

式(28)中，对任意t∈[0,T]，存在唯一的k使得kΔ≤t<(k+1)Δ，根据假设1.1，可得

(29)

代入式(28)可得

(30)

由式(26)、(27)和(30)可知，对任意t∈[0,T]，

对式(22)中的κ满足κ1-pup<1，有

(31)

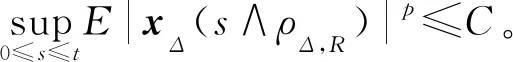
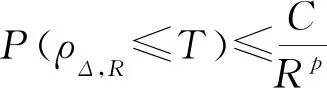
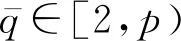
(32)

证明：令θΔ,R=τR∧ρΔ,R，eΔ(t)=x(t)-xΔ(t)，则有

(33)

令δ>0是任意的，利用Young不等式

得到

由引理2.1和2.2可知，

推导得出

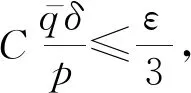
为此，对x,y∈n，定义截断函数

可以看出，当|x|∨|y|≤R时，有f(x,y)=FR(x,y),g(x,y)=GR(x,y),同时由|x|∨|y|≤μ-1(h(Δ))可知

fΔ(x,y)=F1(x,y)+FΔ(x,y)=

f(x,y)=FR(x,y)

gΔ(x,y)=G1(x,y)+GΔ(x,y)=

g(x,y)=GR(x,y)

定义以下中立型随机比例微分方程

d[w(t)-D(w(qt))]=FR(w(t),w(qt))dt+

GR(w(t),w(qt))dB(t),t≥0

(34)

初值w(0)=x(0)，FR,GR满足局部Lipschitz条件，因此方程(34)有局部唯一解w(t)，可知

P{x(t∧τR)=w(t∧τR),∀t∈[0,T]}=1

(35)

另一方面，对每个步长Δ∈(0,Δ*]，利用经典的EM算法得到方程(34)连续时间的连续数值解记为wΔ(t)，且有

P{x(t∧ρΔ,R)=w(t∧ρΔ,R),∀t∈[0,T]}=1

(36)

考虑式(35)和(36)，得到

则有

因此得到

定理证毕。

3 算例分析

考虑以下中立型随机比例微分方程

(37)

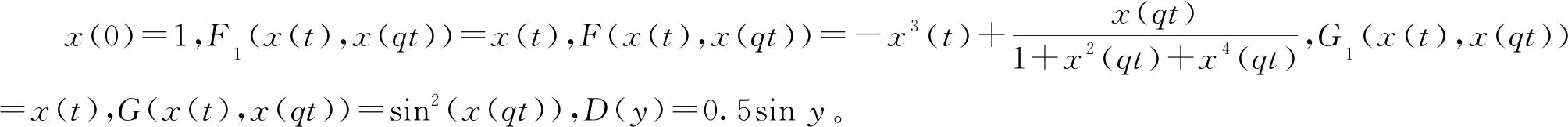
对于假设1.1、1.2和1.4，方程显然成立。下面证明方程满足假设1.3。

接下来选取μ(·),h(·)，已知

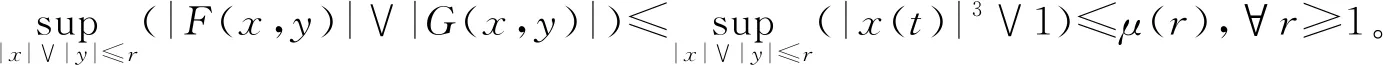
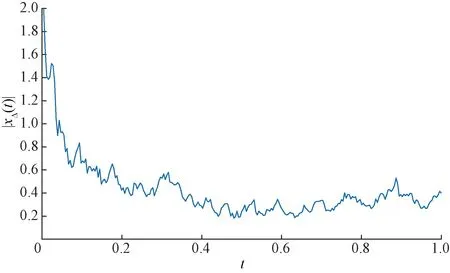
图1 数值解随时间变化图

4 结 语

研究了中立型随机比例微分方程的数值解问题，利用部分截断EM方法建立了连续时间的数值解，通过一系列不等式技巧对中立项和比例时滞项进行处理，得到数值解的Lp有界性，继而证明方程的收敛性。但本研究的研究对象是满足假设1.3的一类具有特殊特征的高度非线性中立型随机比例微分方程，研究结论不能涵盖条件更一般的高度非线性中立型随机比例微分方程，这也将是以后的研究方向。