多维关联规则的分布式能源系统数据挖掘方法研究

2022-11-11宋善坤

能源与环保 2022年10期

宫帅，宋善坤

(1.国网安徽省电力有限公司信息通信分公司，安徽合肥 230041； 2.安徽继远软件有限公司，安徽合肥 230093)

分布式能源系统可以在较少的成本投入下，满足较高的供电需求，还可以将输电损耗量控制在最低。与传统能源系统相比，分布式能源系统克服了损耗高的弱点，能够有效节约能源消耗、降低企业人力物力成本。因此，各国研究人员不断进行了更深层次的研究，通过提升相关配套设备开发速度，以期为新时代下能源产业与电力工业的发展提供重要的保障。

分布式能源系统具有分布存储以及数据量大等特点，工作人员难以全面掌握能源运行规律，无法及时发现数据可能存在的异常点。为确保其稳定运行，需要对其运行数据进行挖掘。国内相关学者对此进行了深入分析，例如文献[1]利用多层次模糊关联规则对高频项目集不断进行自上而下地挖掘，同时引入模糊集合理论和多层分类技术，从事务数据集中找到合适的模糊关联规则进行挖掘。该方法可以在多层次的结构中实现数据精准挖掘，但在算法初期并未对数据进行预处理，可能存在多种类型信息，影响最终的挖掘结果；文献[2]利用E-SLMCM和DE-SLMCM算法，将数据库转换为垂直格式，通过两次遍历数据库，记录下各个事件项的时间戳。利用新的求项集时间戳重复计算更高项集的时间戳，以达到理想的数据挖掘结果。该方法对于小规模数据挖掘效果很理想，但对于规模稍大的数据却无法满足挖掘需求。

为此，本文根据多维关联规则获取系统数据特性，保证在完全未知环境下，从海量数据中迅速找到所需内容，即使存在较大的噪声也不受影响，因此提出了一种多维关联规则的分布式能源系统数据挖掘方法。

1 分布式能源系统数据挖掘

1.1 数据预处理

为了防止采集的数据出现重复和格式不统一的情况，在进行数据挖掘之前将所有数据都进行离散化处理，将具体的数据转换为仅能出现一次的字母或者数字，以此来满足实际的挖掘需求[3]。

1.2 分布式能源数据支持度和置信度计算

关联规则可以准确反映各个事务之间存在的某种关联或者依存关系。通常情况下，关联规则可以描述分布式能源数据库中各个数据属性和变量之间的隐藏关系。

假设I={i1，i2，… ，im}表示项Item的集合，D代表的是事务集合，T是I中的一个子集，T⊆I，其中D={T1，T2，… ，Tn}。任意给定一个X和一个Y，假设二者都是T中的项或集[4]，且满足条件X∩Y=φ，那么关联规则为X⟹Y(S%，C%)。其中S、C含义如下所示：

S代表的是支持度(Support)，计算公式见式(1)：

S%={T：X∪Y⊆T，T∈D}/|D|

(1)

C代表的是置信度(Confidence)，计算公式见式(2)：

C%=C(X⟹Y)

(2)

关联分析的目的是挖掘强关联规则，则需要满足下列3个条件。

X∈I，Y∈I且X∩Y=∅

(3)

S(X⟹Y)≥mins

(4)

C(X⟹Y)≥minc

(5)

通过上述公式说明，当预先设定的阈值大于最小支持度mins和最小置信度minc时，该规则就属于强关联规则[5]。

1.3 数据立方体生成

在数据库内，数据通常以数据立方体的形式组织与存储。维和事实共同构成了数据立方体，维代表的是看数据的角度，维的取值被称为维成员[6]；事实中包含了大量与维相关的关键字和事实度量。

根据每个用户实际的挖掘需求，在数据库内建立相应的数据立方体，然后在这些立方体上进行数据的挖掘。由于数据立方体一开始被全部或部分物化存储[7]，使得在后续的多维关联规则数据挖掘中节省了一部分时间成本，在一定程度上提高了挖掘效率。

在多维关联规则挖掘任务中，内容包含了d1，d2，… ，dn维。首先需要明确维的层次数量，以此生成相应的数据立方体。每个维中包含了|di|+1个数值，|di|代表了第i维中维成员的数量。di中最后一行被称为“SUM”，它记录了其所对应所有维的总值。数据立方体中也包含了所有维成员的频繁度量值[8]，用count来表示。

以分布式能源系统中存储的数据作为立方体的主要生成内容。具体点说，就是将系统中的数据与各相关表进行关联，统计各个维度组合后的总值[9]。将系统中的数据按照维度划分为3类，分别是操作维、运行维和执行维。每个维度又由若干个子维度[10]构成，操作维中包括了时间和操作记录在内，运行维中集合了正常/异常运行状态以及运行时间，执行维中主要是正常/异常执行记录和执行时间。

在实际的应用中，根据上述各个子维度作为数据立方体的维度，生成立方体的过程可以通过SYBASE IQ中的立方体生成功能来实现，以确保高效、灵活地完成生成工作。SYBASE IQ是一种关系型数据库[11]，专门服务于大型数据库，因其具有独特的按列存储机制和多样化的索引机制[12]，即使面对规模庞大的数据，依然可以高效完成数据立方体的生成工作。

2 多维关联规则算法的应用

关联规则分为单维关联规则、维间关联规则和多维关联规则。顾名思义，单维关联规则就是只含有一个关键谓词，而多维关联规则中则包含了如地点、人物、原因等多个谓词[13]，并且谓词与谓词之间可以通过两两组合的形式得到更多谓词的有效规则，维间规则指含有一个关键谓词，但是谓词却具有多种不同的属性。

Apriori算法在挖掘关联规则频繁项集方面具有非常明显的优势，该算法利用逐层搜索的迭代方式，不断探索生成项集。本文根据分布式能源系统的实际需要，对Apriori算法作出部分改进，利用不产生候选项[14]的FP-树(Frequent Pattern-growth，频繁模式树)增长算法实现对分布式能源系统的数据挖掘。多维关联规则算法流程如图1所示。

图1 多维关联规则算法流程Fig.1 Flow chart of multidimensional association rule algorithm

2.1 多维关联规则算法实现过程

(1)生成(1-项集)频繁项集。将挖掘的对象看作是数据库F，对F进行第一次扫描并对所有维生成(1-项集)频繁项集，得到每个维的支持度计数(频繁性)，根据置信度找出全部单个候选项集。此时由于数据维度较高，因此对置信度进行改进，利用全置信度单个候选项集进行查找，全置信度的计算公式如下：

(6)

对式(6)进行简化，结果表示为：

C′(X)=min{P(X|Y)，P(Y|X)}

(7)

通过分析式(2)可知，其与关联规则X⟹Y置信度的表达式是相关的，所以得到了关于规则的全置信度概念，其计算公式如下：

C″(X⟹Y)=min{C(X⟹Y)，C(Y⟹X)}

(8)

根据全置信度以及维数的不同划分频繁项集[15]，并根据每个组中支持度最大的项，对组间按照从大到小的顺序排列，组内同样按照从大到小的顺序对支持度[16]进行排列，以此找出全部单个候选项集。排列结果集可用表格描述。表1展示的是一组多维事务表，假设最小事务的支持度计数为2(即)，得到的结果集为L=[F1：5，F3：4，A2：4，A1：3，A3：3，B1：4，C1：4，]。

结合上述分析，将分布式能源系统的事件集合定义为{E1，E2，E3，E4，E5}，其中，E1代表的是能源存储异常波动情况，E2代表的是温区PID(Packet Identifier，数字控制显示)异常，E3代表的是系统能源传输异常，E4代表的是能源分布调整，E5代表的是能源存储调整。随着分布式能源系统运行，产生了9种状态事务，即|D|=9，具体内容见表2，设定E1⟹E5规则出现了异常。

表2 分布式能源系统中的事务状态Tab.2 Transaction status in distributed energy system

将每一种状态信息用不同的Tid来表示，借助专家系统对运行过程中频繁项的动态数据库的字典序进行存储，以及寻找D中的频繁项集。

(2)FP-树的构建。第2次扫描数据库F，并对事务中的项进行排序操作。挖掘频繁2项集(2-项集)时，如果直接均分数据然后分配到每个候选项集中，虽然操作简单，但是每条事务的个数不同，查找2项集的运算量不同，导致FP-树构建效率与质量下降。所以利用ψi来表示在第i条事务中查找2项集所需要的运算量，其中ti表示第i条事务中的项目个数，则ψi计算公式如下：

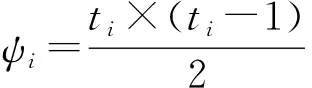
(9)

由于不同的等价类在挖掘频繁项集的运算复杂度不同，将这些任务分配给不同的FP-树节点进行处理会导致负载不均衡，因此采用Wi表示频繁2项集中第i个等价类的权重值，按权重值的降序排列，让每个节点分配尽量相同的权重累加值的等价类，以此保证负载均衡性。Wi的计算公式如下：

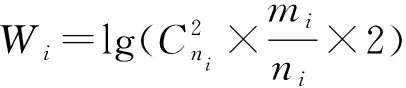
(10)

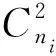
结合上述分析，将候选项集中的非频繁项删除掉，单独建立一个分枝[17]。本文构建的FP-树如图2所示。

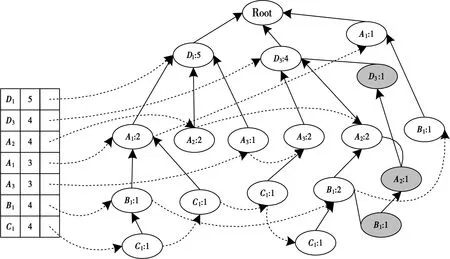
图2 本文构建的FP-树Fig.2 FP-Tree constructed in this paper

(3)对构建的FP-树作出部分修正。计算图2中所有叶子节点的支持度计数[18]，如果存在某个节点所有孩子节点支持度计数总数、小于该节点的支持度计数，那么就需要计算这个节点以及该节点所有双亲节点对应的支持度计数。图2中的灰色B1节点，经过复制后将得到新枝，从FP-树中分离出来，重新构建新的FP+树，原始FP-树节点的支持度计数在不断减少，减少的支持度计数用FP′来表示，经过修正处理后的FP-树节点支持度计数可提高挖掘精度。

(4)剪枝处理。对于频繁FP-树，利用修正算法挖掘频繁模式，并通过剪枝处理去除掉冗余数据，使得最终挖掘结果更加准确。对节点A1剪枝就是删除节点A1，用该节点的所有双亲节点支持度计数与该节点原始支持度计数做减法处理[19]。经过剪枝处理后，剩余的节点[20]信息即为最终的分布式能源系统数据挖掘结果。

2.2 在分布式能源系统数据挖掘中的应用

将最小支持度的计数设置为3，即Smin=3，通过构建FP-树生成候选项集和频繁项集，过程如下。

(1)对分布式能源系统进行第1次扫描，得到D中所有候选项的计数。将频繁l-项集的集合定义为L1，由多个支持度为最小值的候选l-项集组合在一起而形成。

(2)进行第2次扫描，得到频繁2项集的集合为L2，通过L1计算得到候选2项集的集合C2。在剪枝的过程中，如果发现对象子集为频繁子集，则不需要进行删除操作。

(3)在第3次扫描中，计算L2得到候选3项集的集合为C3，直接对其进行剪枝操作。频繁项集下的非空子集同样也是频繁的。举个例子说明，{E1，E3，E5}的2项子集是{E1，E3}、{E1，E5}和{E3，E5}。由于L2中不存在，所以{E3，E5}不是频繁的。在C3中删除{E1，E3，E5}，得到的剪枝结果为C3={E1，E2，E3}，{E1，E2，E5}。

(4)进行最后一次扫描，计算L3得到候选4项集的集合为C4。L3={E1，E2，E3，E5}，根据FP-树的思想，由于它的子集{E2，E3，E5}不是频繁的，所以直接剪枝删除掉，由此可得C4=∅，算法结束。通过上述四个步骤，本文方法将所有频繁项集全部找出，根据最小可信度可得到以下几种关联规则。

E1⟹E2：支持度计数为3，置信度3/6=50%，大数据项集为L[2]；

E1⟹E5：支持度计数为6，置信度6/6=100%，大数据项集为L[2]；

E2⟹E3：支持度计数为2，置信度2/8=25%，大数据项集为L[2]；

E3⟹E5：支持度计数为6，置信度6/8=75%，大数据项集为L[3]；

E1、E2⟹E3：支持度计数为3，置信度3/6=50%，大数据项集为L[3]；

E4、E5⟹E2：支持度计数为4，置信度4/5=80%，大数据项集为L[3]。

通过观察以上几种关联规则，可以发现本文所采用多维关联规则算法能够准确挖掘出E1⟹E5这个规则出现了异常，符合设定值，异常情况为能源存储结构异常波动。工作人员可根据此结果及时进行调整，适当地删减和添加，确保分布式能源系统长期稳定地运行。

选取了5个专门用来测试多维关联规则数据挖掘算法的数据集作为测试数据库，容量大小分别是334 KB(chess)、557 KB(mushroom)、3 970 KB(retail)、8 820 KB(connect)、15 900 KB(pumsb)。将最小支持度的阈值设置为0.2，计算到频繁4项集为止。3种方法在上述环境下进行数据挖掘，结果见表3。