环向裂纹缺陷压力管道塑性极限载荷安全性分析

萨如丽

(青海省化工设计研究院有限公司，青海 西宁 810008)

在工程领域实际生产中的构件都存在结构不规则和受载复杂的问题，应用解析法很难求解，所以人们针对此类问题引用了数值模拟方法[1]。在役管道产生缺陷的原因有很多，并且存在的缺陷种类也有很多。因此，严格保证管道的安全、准确计算管道使用寿命成为研究重点[2]。我国大多数压力管道都由韧性较好的中低强度的钢材料制成，失效模式通常为塑性破坏失效[3]，需要精确地计算不同缺陷压力管道的塑性极限载荷，并制定出一种适合工程上使用的安全评定方法。

1 正交试验计算方案

存在很多因素影响环向裂纹压力管道的塑性极限载荷，包含材料、壁厚和裂纹尺寸。为了研究各因素对裂纹管道承载能力的影响规律，本文采用正交试验方法进行试验，得出各因素对承载能力的影响程度。本文在编制正交表时，选择影响管道极限载荷的4个因素，每个因素取5个水平，确定25个试验方案，得到了正交图[4]。

对不存在缺陷的管段可以用极限载荷计算，见式(1)：

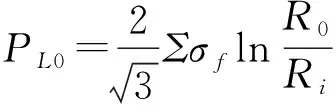
(1)

(2)

式中，PL0为极限内压；MB0为极限弯矩。

对于含有缺陷的管段由于每种管段的壁厚、内外径等都是不一样的，同时裂纹的轴及环向长度、深度都会对裂纹的缺陷有影响。在确定唯一自变量的条件下，如内压、弯矩分别恒定，确定内压和弯矩的关系[5]。

在内压恒定条件下，裂纹缺陷在内压或者拉力条件时，中心轴角和未环向半角，满足公式：

(3)

式中，β=arcsin(Asinθ) ，当r>1.1时，为厚壁管道；当r≤1.1时，为薄壁管道。

(4)

当r≤1.1时，取m=1，A=0.5x，式中：β=arcsin(0.5x)，σm极限弯矩为0时 ，当r>1.1时，其中θ+β<π时，塑性极限弯矩公式为：

(5)

θ+β≥π时， 塑性极限弯矩公式为：

(6)

1.1 裂纹缺陷规则化

根据公式(1)—式(6)进行计算，裂纹缺陷的形貌，测得缺陷沿壁厚方向的深度为B，沿轴向的长度为A，沿环向的裂纹角为2°，进行规则化，将规则化后的缺陷尺寸无量纲化。正交实验如图1所示。

图1 正交实验Fig.1 Orthogonal experiment

如图1所示，根据数据做正交实验图，其中轴向长度、相对环向长度、相对深度、管径比，分为25组，每组因素确定5个相同的数据，如：轴向长度方案1—方案5的数据为0.05，方案6—方案10数据为0.1，方案11—方案15数据为0.15，方案16—方案20数据为0.2；相对环向长度方案1为0.2，方案25为1.0，中间间隔0.2；管径比分别取1.05、1.10、1.15、1.20、1.25。

1.2 极限载荷(无缺陷压力管道)

压力管道无缺陷时，隐藏裂纹会在管道内部，在管道输送介质时，会因为温度压力等影响，使裂纹初始发展[6]。选取20号钢，管道规格分别为φ32 cm×3 mm，φ47 cm×4 mm，φ57 cm×3.5 mm，φ89 cm×4 mm，φ159 cm×4 mm，无缺陷压力管道在不同载荷工作用的塑性极限载荷公式计算极限内压PL0及弯矩ML0。无缺陷压力管道极限载荷理论值与有限元值如图2所示。

2 压力管道塑性极限载荷的确定

含裂纹压力管道在使用过程中，由于内压及外载荷的作用会逐渐产生塑性失效，直至断裂。裂纹及管道本身存在影响裂纹扩展的因素，如裂纹环向长度、径向深度、轴向宽度及管道自身直径，以这4个参量作为影响极限载荷规律的因素[7]。

计算方案分析裂纹管道只受内压载荷作用的极限内压P*；分析裂纹管道只受弯矩载荷作用的极限弯矩M*；计算裂纹管道在受内压、弯矩不同比例组合作用下的塑性极限载荷，施加载荷分别为0.2PL+MB、0.4PL+MB、0.6PL+MB、0.8PL+MB。

根据内压值的变大，管道承载能力变小，塑性区域面积逐渐变大。不同因素水平交互作用和实验误差都会影响正交试验结果，在内压载荷作用下，应用直观分析法，计算影响管道承载能力4个因素的极差，作出趋势图，观察每因素的水平对结果不同影响趋势，找出最优水平组合[8]。根据图2呈现的趋势可知，由于不同因素的影响程度，管道的承载能力有所减弱。深度对管道的承载能力影响最大，当相对深度b>0.5后，管道变形幅度比较明显；其次裂纹的环向长度对管道的承载能力影响也较大，虽然数值减少幅度相对平缓，但最值之差较大；轴向长度和管径比影响管道的极限内压相对很小，无明显数值变化[9]。压力管道极限载荷如图3所示。

图3 压力管道极限载荷Fig.3 Extreme load diagram of the pressure pipe

由图3可知，在纯内压作用下，对管道承载能力影响最大的因素是裂纹缺陷深度，其次是环向长度，而其他2个因素对裂纹的扩展及管道的位移变形影响不大。根据以上结论选取裂纹深度和环向裂纹尺寸影响因素，分析不同的相对深度和相对裂纹长度对管道的极限内压载荷具有不同的影响针对工程问题，应用理论方法得到的缺陷压力管道极限载荷比较繁琐，可以利用有限元法得出的数值对工程问题进行拟合公式，进而估算极限载荷[10]。由于缺陷管道承载能力较无缺陷管道承载能力小，利用修正系数修正无缺陷管道极限载荷公式，得出含环向裂纹缺陷管道的极限内压载荷计算公式。根据以上结论得相对裂纹深度和环向裂纹长度对含环向裂纹管道的承载能力影响较大[11]。

3 纯弯矩作用下有限元结果分析

裂纹管道在单一弯矩分别为6.35、11.02、26.03 kN·m作用下的裂纹管道塑性区的扩展情况及失效模式，具体如图4所示。

图4 纯内压下各因素影响规律Fig.4 Rule of various factors under pure internal pressure

不同因素水平及交互作用和实验误差都会影响正交试验结果，在纯弯矩载荷作用下，应用直观分析法，对影响管道承载能力的4个因素作极差分析分析。作出趋势图，观察不同的趋势图，得出最优水平组合[12]。相对裂纹深度对无量纲内压的影响如图5所示。由图5可知，在纯弯矩作用下管道的承载能力受裂纹相对深度影响最大，其次是裂纹环向长度，轴向长度和管径比影响管道承载能力及位移变形很小，而且相差不大。当环向内表面裂纹缺陷的相对深度b>0.4时，曲线下降幅度明显加大，而相对环向长度下降趋势较相对深度平缓些[13]。因此，相对深度影响纯弯矩下压力管道承载能力程度最大。相反，轴向长度和管径比对纯弯矩下管道的承载能力影响不大，但由于管径比值的逐渐增大，曲线平稳上升，可见在纯弯矩作用下，薄壁管道比厚壁管道的承载能力低，较易发生断裂或泄漏。根据以上结论选取裂纹深度和环向裂纹尺寸影响因素，分析不同的相对深度和相对裂纹长度对管道的无量纲极限弯矩载荷的影响[14]。相对裂纹长度对无量纲内压的影响如图6所示，相对裂纹趋势如图7所示。

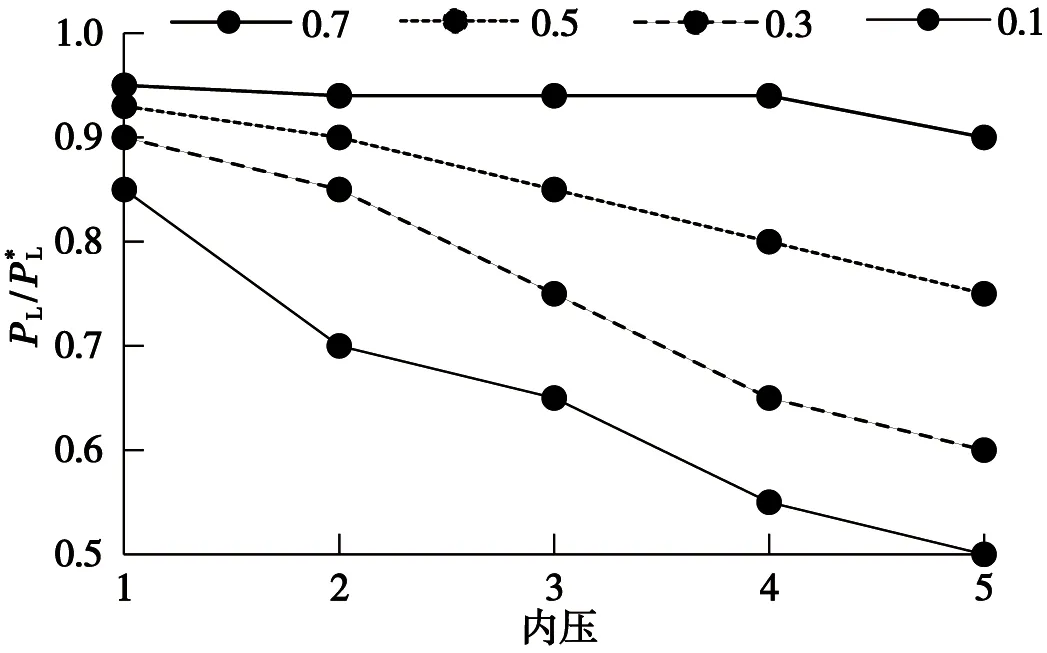
图5 相对裂纹深度对无量纲内压的影响Fig.5 Effect of relative crack depth on dimensionless internal pressure

图6 相对裂纹长度对无量纲内压的影响Fig.6 Effect of relative crack length on dimensionless internal pressure

图7 相对裂纹趋势Fig.7 Relative crack trend chart

相对裂纹深度对无量纲弯矩的影响如图8所示。

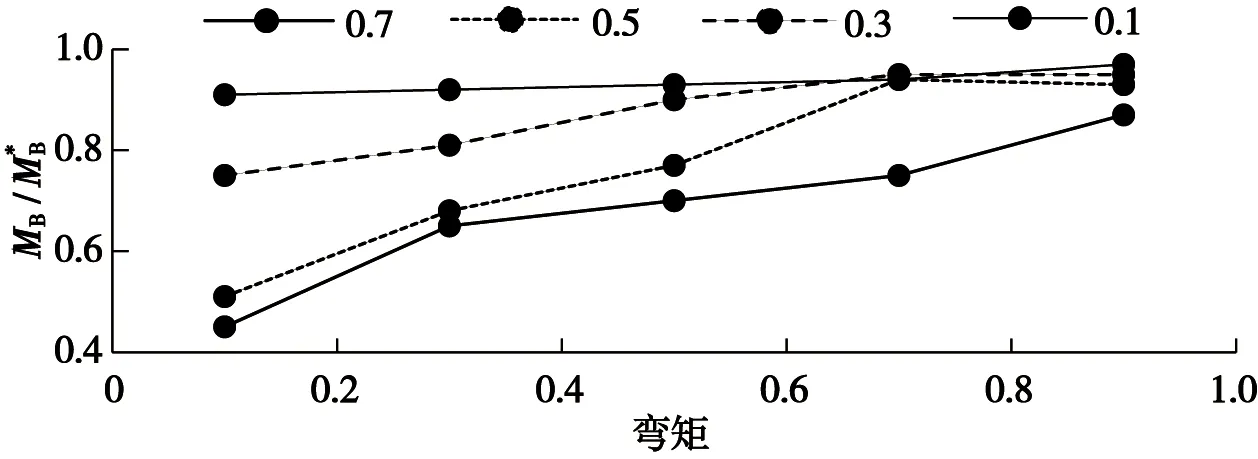
图8 相对裂纹深度对无量纲弯矩的影响Fig.8 Effect of relative crack depth on dimensionless bending moments

当得到的极限内压与极限弯矩载荷值在曲线内部时，说明裂纹管道是安全的。针对本文研究的实验管道，当相对裂纹深度值最大时，即b=0.9时，其中试验号19号和22号对应的无量纲内压和弯矩不符合。因此，这2个裂纹缺陷管道是不安全的[15-16]。

相对裂纹长度对无量纲弯矩的影响如图9所示。

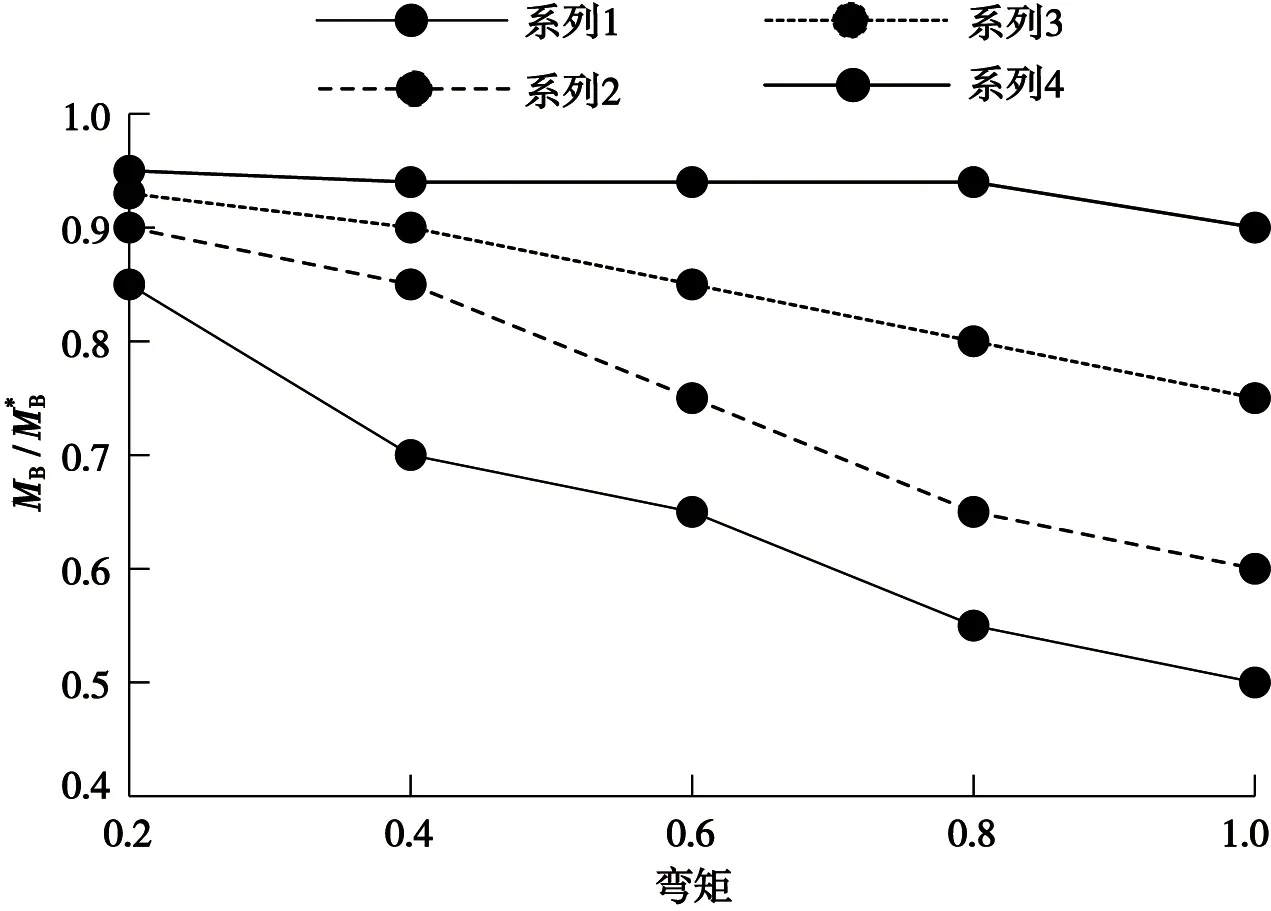
图9 相对裂纹长度对无量纲弯矩的影响Fig.9 Effect of the relative crack length on dimensionless bending moments

4 结语

应用非线性有限元方法计算环向内表面裂纹应力管道的极限载荷，得到相关结论：分别在单一内压、单一弯矩及组合载荷作用下，比较裂纹尺寸和管道尺寸对塑性极限载荷的影响程度，得出4个因素一次影响程度：深度>长度>轴向长度>管径。取影响程度较大的2个因素深度和长度的无量纲进行数据处理，分别在单一内压、单一弯矩载荷工况下，对内压和弯矩无量纲进行拟合修正系数，得到修正后的塑性极限载荷值，得到的曲线对不同环向裂纹缺陷管道进行安全性分析。