4-维幂零李代数的Hom-Lie代数结构
2022-11-11林丽芳曾月迪陈梅香
林丽芳,曾月迪,陈梅香
(莆田学院数学与金融学院,福建 莆田 351100)
0 引言
在研究向量场上Witt代数和Virasoro代数的量子形变时,Hom-Lie代数的结构得到了学者的关注与研究[1].Hom-Lie代数作为李理论的一个重要研究方向,与李代数有着十分密切的关系.近年来一些特殊李代数上的Hom-结构得到了充分研究,比如一个5-维可解李代数[2]、(n-3)-filiform李代数[3]、扭Heisenberg李代数[4]、李代数W(2,2)[5].作为一类重要的李代数,幂零李代数的结构和表示在李理论的研究中占有重要地位.GRAAF[6]通过确定基元的方法给出了低维幂零李代数的分类.本文根据低维幂零李代数在同构意义下的分类,确定了4-维幂零李代数的Hom-李代数结构.
1 预备知识
定义1[1]设L为域上的向量空间,带有线性映射α:L→L,L上定义一个乘法运算[-,-]:L×L→L(称为方括号),如果满足以下条件:
(i)α[x,y]=[α(x),α(y)], ∀x,y∈L;
(ii)[λ1x1+λ2x2,y]=λ1[x1,y]+λ2[x2,y], ∀λ1,λ2∈, ∀x1,x2,y∈L;
(iii)[x,y]=-[y,x],∀x,y∈L;
(iv)Hom-Jacobi等式:
[(α+Id)(x),[y,z]]+[(α+Id)(y),[z,x]]+[(α+Id)(z),[x,y]]=0, ∀x,y,z∈L,
则称(L,[-,-],α)为域上的一个Hom-Lie代数,当α=Id时,Hom-Lie代数就为Lie代数.
GRAAF[6]对低维幂零李代数的结构做出了如下分类:
引理[6]设L是特征为0的代数闭域上维数等于4的幂零李代数,e1,e2,e3,e4是L的一组基,则在同构的意义下,仅有如下三类(其中没有写出来的基元方括号运算为0):
L4,1:[ei,ej]=0;L4,2:[e1,e2]=e3;L4,3:[e1,e2]=e3, [e1,e3]=e4.
下面研究4-维幂零李代数L4,1,L4,2,L4,3上的Hom-Lie代数结构,也就是确定其上的满足Hom-Jacobi等式的自同态.
2 主要结论
定理1 对于任何一个双线性同态映射α,(L4,1,α)均可构成一个Hom-Lie代数.
证明 因为L4,1是可交换李代数,基元上的方括号运算等于0,即[ei,ej]=0,i,j=1,2,3,4,所以对于任何一个双线性同态映射α,α保持基元的方括号运算和Hom-Jacobi恒等式,也即(L4,1,α)构成一个Hom-Lie代数.
定理2 若(L4,2,α)是一个Hom-Lie代数,则Hom-同态α在L4,2的基元上的作用可表示为
其中,a11a24-a21a14=0,a12a24-a22a14=0,a31,a32,a41,a42,a34,a44为任意常数.
证明 假设Hom-同态α在L4,2的基元上的作用为
将α作用在[e1,e2]=e3上,可得[α(e1),α(e2)]=α(e3),即
[a11e1+a21e2+a31e3+a41e4,a12e1+a22e2+a32e3+a42e4]=a13e1+a23e2+a33e3+a43e4.
根据L4,2的基元运算,比较两边系数有
a13=a23=a43=0,a33=a11a22-a21a12.
(1)
将α作用在[e1,e4]=0上,可得[α(e1),α(e4)]=0,比较两边系数有
a11a24-a21a14=0.
(2)
将α作用在[e2,e4]=0上,可得[α(e2),α(e4)]=0,比较两边系数有
a12a24-a22a14=0.
(3)
因为L4,2上的基元运算为[e1,e2]=e3,而e3与其他基元的方括号运算为0,所以α显然满足Hom-Jacobi等式:
[α(ei),[ej,ek]]+[α(ej),[ek,ei]]+[α(ek),[ei,ej]]=0, 1≤i,j,k≤4.
结合(1)(2)(3)式,即得Hom-同态α在L4,2的基元上的作用如定理2.
定理3 若(L4,3,α)是一个Hom-Lie代数,则Hom-同态α在L4,3的基元上的作用可表示为如下四种情况:


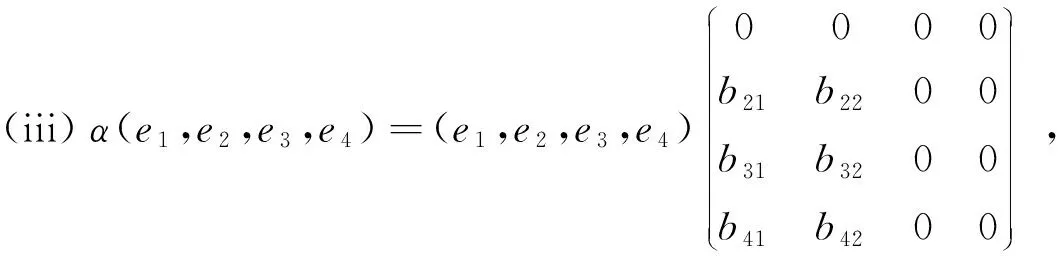
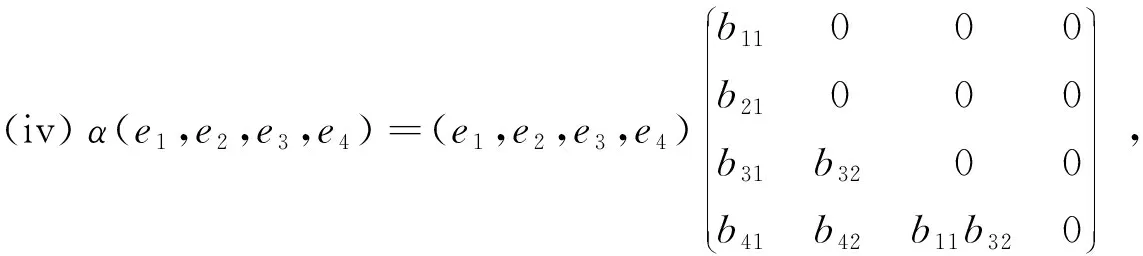
证明 假设Hom-同态α在L4,3的基元上的作用为
由于[e1,e2]=e3,[e1,e3]=e4,即方括号运算结果仅含有e3,e4,而α保持方括号运算,比较运算两边系数可知α(e3),α(e4)中含有e1,e2的系数都为0,即
b13=b23=b14=b24=0.
(4)
将α作用在[e1,e2]=e3上,可得[α(e1),α(e2)]=α(e3),比较两边系数,并结合(4)有
b11b22-b21b12=b33,
(5)
b11b32-b31b12=b43.
(6)
将α作用在[e1,e3]=e4上,可得[α(e1),α(e3)]=α(e4),比较两边系数并结合(4)有
b34=0,
(7)
b44=b11b33.
(8)
将α作用在[e2,e3]=0上,可得[α(e2),α(e3)]=0,比较两边系数并结合(4)有
b12b33=0.
(9)
因为L4,3上的基元运算为[e1,e2]=e3,[e1,e3]=e4,e4与其他基元的方括号运算为0,α(e3),α(e4)中e1的系数为0,所以α显然满足Hom-Jacobi等式:
由(9)可知,b12,b33的取值分为b12=0,b33≠0;b12≠0,b33=0;b12=0,b33=0三种情况.
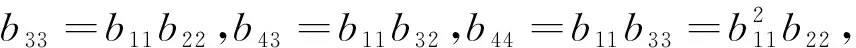

当b12=0,b33=0时,式(5)(6)(8)可化为
b11b22=0,
(10)
b11b32=b43,
(11)
b44=0.
(12)
由(10)可知,b11的取值分为b11=0和b11≠0两种情况.
当b11=0时,由(11)可知,b43=0,结合(4)(7)(12),即得定理3中第三种情况.
当b11≠0时,由(10)可知,b22=0,结合(4)(7)(11)(12),即得定理3中第四种情况.
