超大直径盾构施工引发的上软下硬地层地表沉降规律①
2022-11-10汤新辉首正勇刘建柯
汤新辉,首正勇,刘建柯
(1.长沙市建设工程质量安全监督站,湖南 长沙 410001;2.广东省重工建筑设计院有限公司,广东 广州 510670)
盾构法施工以其安全性、高效性、实用性等优势在城市隧道工程建设中得到广泛使用。由于盾构施工不可避免地破坏土体稳定,引起隧道周围地层变形和地表沉降,影响隧道施工及周边环境安全[1-2]。Peck建立了隧道开挖引起地表沉降的经验公式[3],因不同地层经验参数取值的差异性,经验公式无法保证沉降预测结果准确性,为此国内外许多学者基于隧道施工实测地表沉降数据,引入不同参数对Peck公式进行修正,使其适用于上软下硬、砂岩及富水砂性等不同地层条件下地表沉降预测,取得了良好效果[4-5]。其中以分析数学为基础的理论解析法,如Mindlin法、虚拟镜像法及复变函数法[6-7]等求解不同边界条件下盾构施工的地层变形问题,工程适用性较好,但存在计算过程复杂、参数选取较多、假定条件脱离实际等缺点,难被工程从业人员所接受。有限元法、有限差分法[8-9]等考虑地质条件、施工工艺等因素,但其本构模型参数确定困难,模拟结果一般不能对沉降值进行准确预测;基于大数据的机器学习算法可快速有效处理多参耦合问题,用于盾构施工预测地表沉降[10-12],但缺乏解释自身推理过程能力,监督学习严重依赖外部标签准确性,难于处理噪声样本,并存在对特殊场地适用性差等问题。本文采用线性回归拟合方法,对Peck公式进行了修正,并将修正Peck公式用于某过江隧道北线超大直径盾构施工引发的上软下硬地层地表沉降量预测。
1 监测数据获取
如图1所示,某过江隧道工程北线隧道长3.32 km,南线隧道长3.63 km,盾构段全长约1.4 km。盾构区间段地表平均高程35.32 m,地貌单元为河流侵蚀-堆积地貌,主要为湘江Ⅳ、Ⅲ、Ⅰ级阶地、河漫滩及河床。施工采用外径15.01 m的超大直径泥水盾构机,单洞洞径14.50 m,隧道洞身主要穿越中~微风化板岩,顶板地层为微风化板岩,隧道上覆土层厚度7.30~26.20 m,隧道开挖横断面多为上软下硬土层,典型断面地质横剖面如图2所示。
图1 工程线位示意图
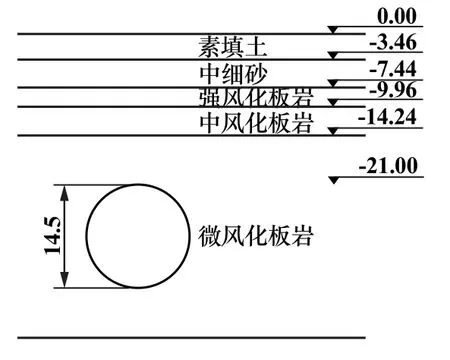
图2 土层地质横剖图(单位:m)
1.1 地表沉降监测
在盾构进出洞50 m范围内,每24 m(12环)布置一个监测剖面,其余位置每40 m(20环)布置一个监测剖面,测点间距及监测点数见图3。测点采用钻孔埋设、天宝dini03电子水准仪观测,监测点与相邻基准点高差中误差小于1.0 mm。
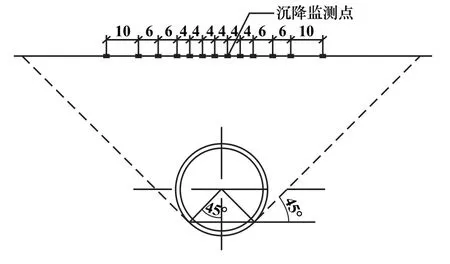
图3 地表沉降监测点布置示意图(单位:m)
1.2 典型断面监测结果分析
监测周期见表1,典型断面横向地面沉降曲线见图4。表明盾构机抵达断面前,地表无明显沉降;盾构机穿越监测断面,地表沉降显著增加;隧道轴心地表沉降值及沉降速率明显大于隧道两侧;随盾构机穿越断面,沉降曲线发展为正态分布曲线,符合沉降槽理论。盾构机穿越监测断面最大地表沉降7.5 mm,盾尾注浆阶段沉降2.74 mm,分别占总沉降量的62.8%及22.9%,盾构机通过后,地表沉降1.51 mm,占总沉降量的12.6%。结合工程地质勘探结果,认为盾构机抵达监测断面前,沉降主要由地下水位下降、上覆软土层发生固结导致;盾构机穿越断面至盾尾注浆完成前,盾身与土体接触,产生剪应力,且盾构机直径略大于隧道管环外径,同步注浆无法瞬间填充管环与土体间隙,周围土层向间隙快速移动,导致地表沉降迅速发生,第3阶段沉降可视为瞬时沉降。注浆完成后,地层缓慢发生固结及流变,最终达到新的应力平衡,地表趋稳。可见,盾构穿越断面以及盾尾注浆完成前,地表沉降显著。
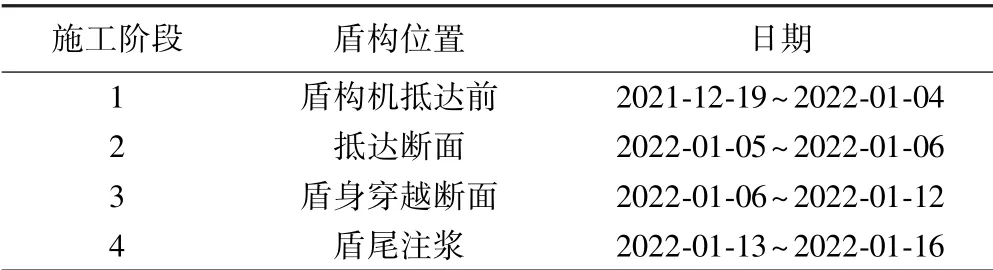
表1 断面1不同施工阶段监测时间
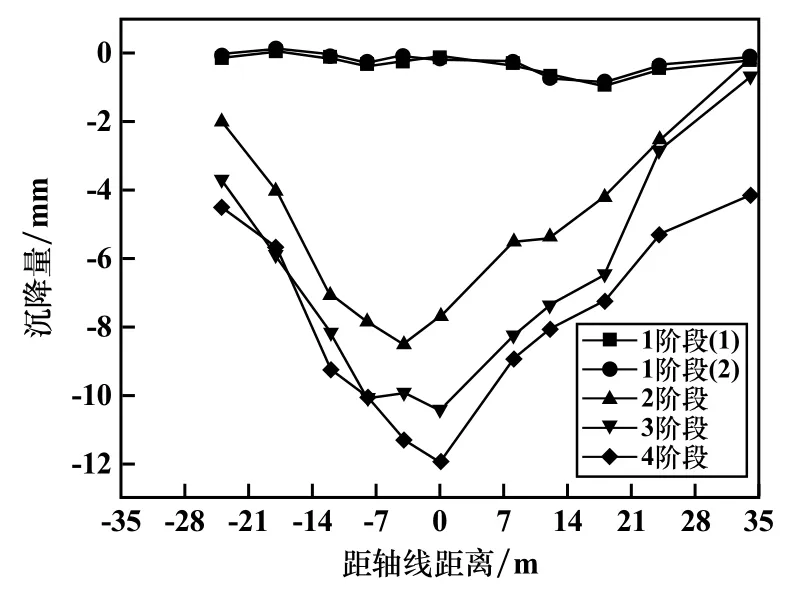
图4 各阶段地表沉降曲线
2 实测数据回归分析
2.1 基于Peck公式的回归分析
如图5所示,Peck公式假设地表沉降槽体积等于不排水条件下的地层体积损失:
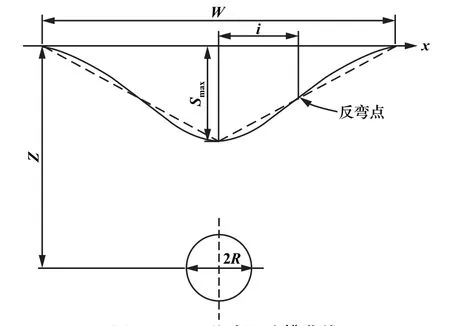
图5 Peck公式沉降槽曲线
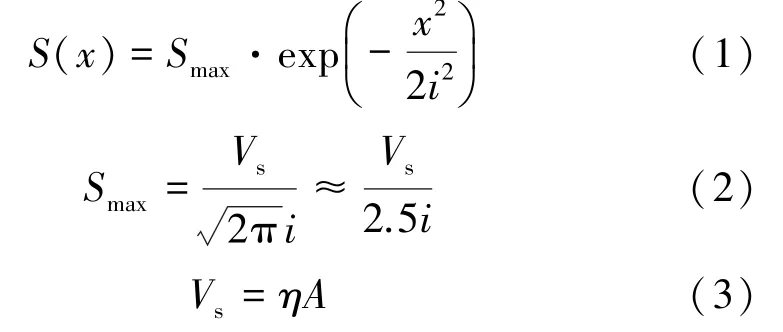
式中x为测点至隧道中轴线的水平距离,m;S(x)为距隧道中轴线距离为x处的地表沉降量,mm;Smax为最大地表沉降量,mm;i为沉降槽宽度,mm;Vs为隧道施工引起的单位长度地层损失量;η为地层体积损失率;A为隧道断面面积,m2。
设K为沉降槽宽度系数,无黏性土K取值0.2~0.3,硬黏土K取值0.4~0.5,软粉质黏土K取值0.7;当地表至隧道中心深度为Z时,i可表示为[13]:

一般中小直径隧道η取值0~2.0%,大直径隧道η取值0~0.5%,随地层条件变好而减小[14]。隧道主要穿越微风化板岩,围岩为Ⅲ级,岩性较好,盾构直径较大,取η=0.3%,K=0.3,R=7.25 m,Z=28.25 m,则:
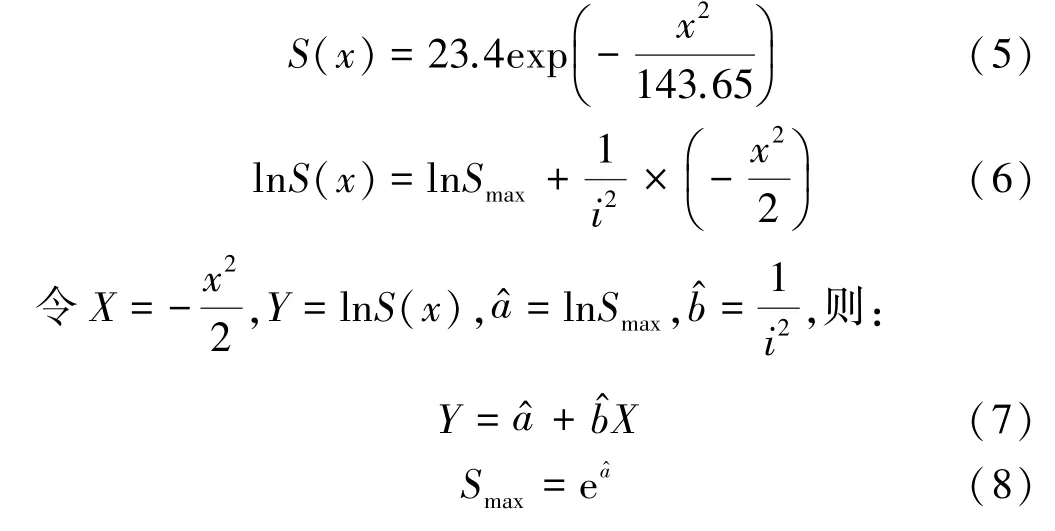
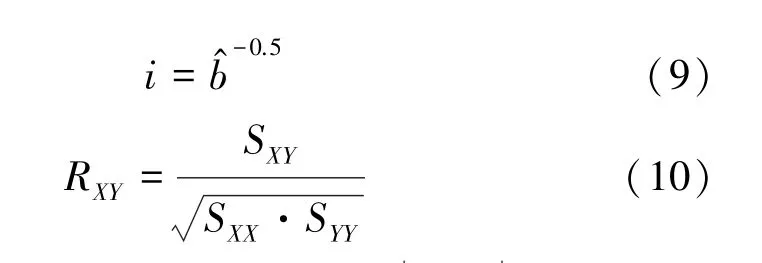
>0.8时,X与Y高相关;时,X与Y显著相关;时,X与Y低相关;时,X与Y不相关。
2.2 实测数据回归分析
随机选取两个断面监测数据对沉降曲线进行拟合,结果见表2~3。
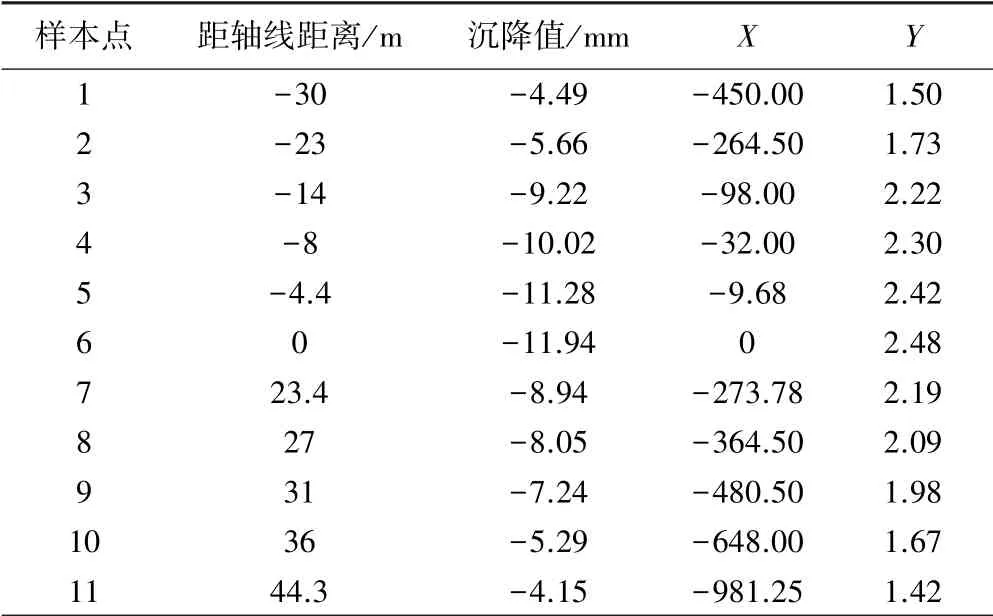
表2 断面1沉降数据回归分析
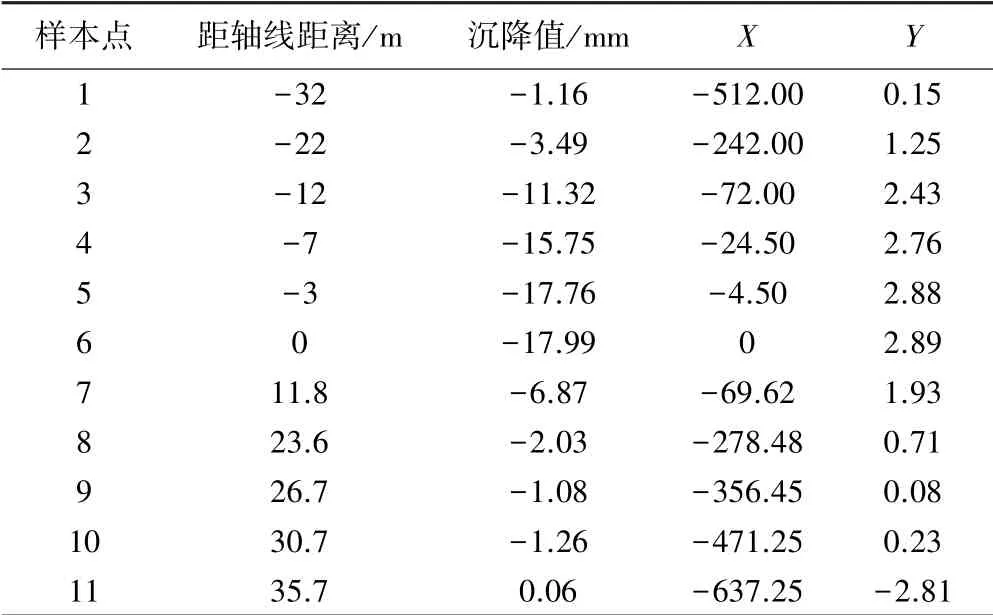
表3 断面2沉降数据回归分析
计算可得:SXX=924 998.16,SXY=970.54,SYY=1.36。得:
断面1:
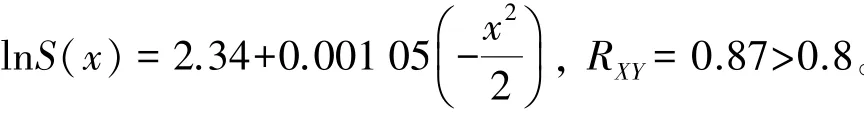
断面2:
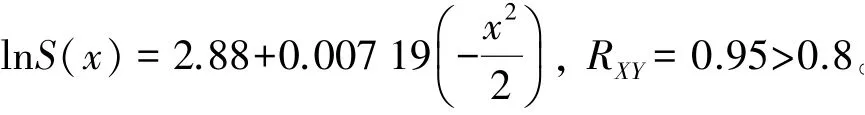
可见2个断面的拟合效果均较好,X与Y为高相关性。
各断面监测数据与回归函数对比见图6。2个断面的拟合曲线、实测沉降曲线与式(5)Peck公式预测结果对比见图7。拟合曲线与实测曲线较为吻合,表明采用线性回归方法,能够对盾构隧道开挖引发的地表沉降进行有效预测。同时,传统Peck公式预测曲线与实际沉降数据曲线偏差较大,不能满足实际工程要求。
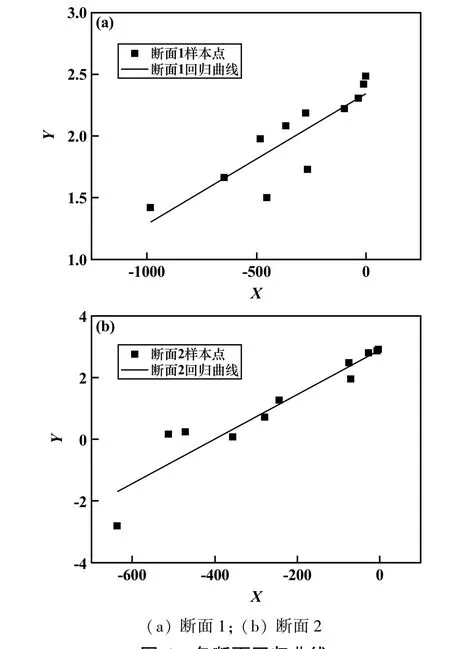
图6 各断面回归曲线
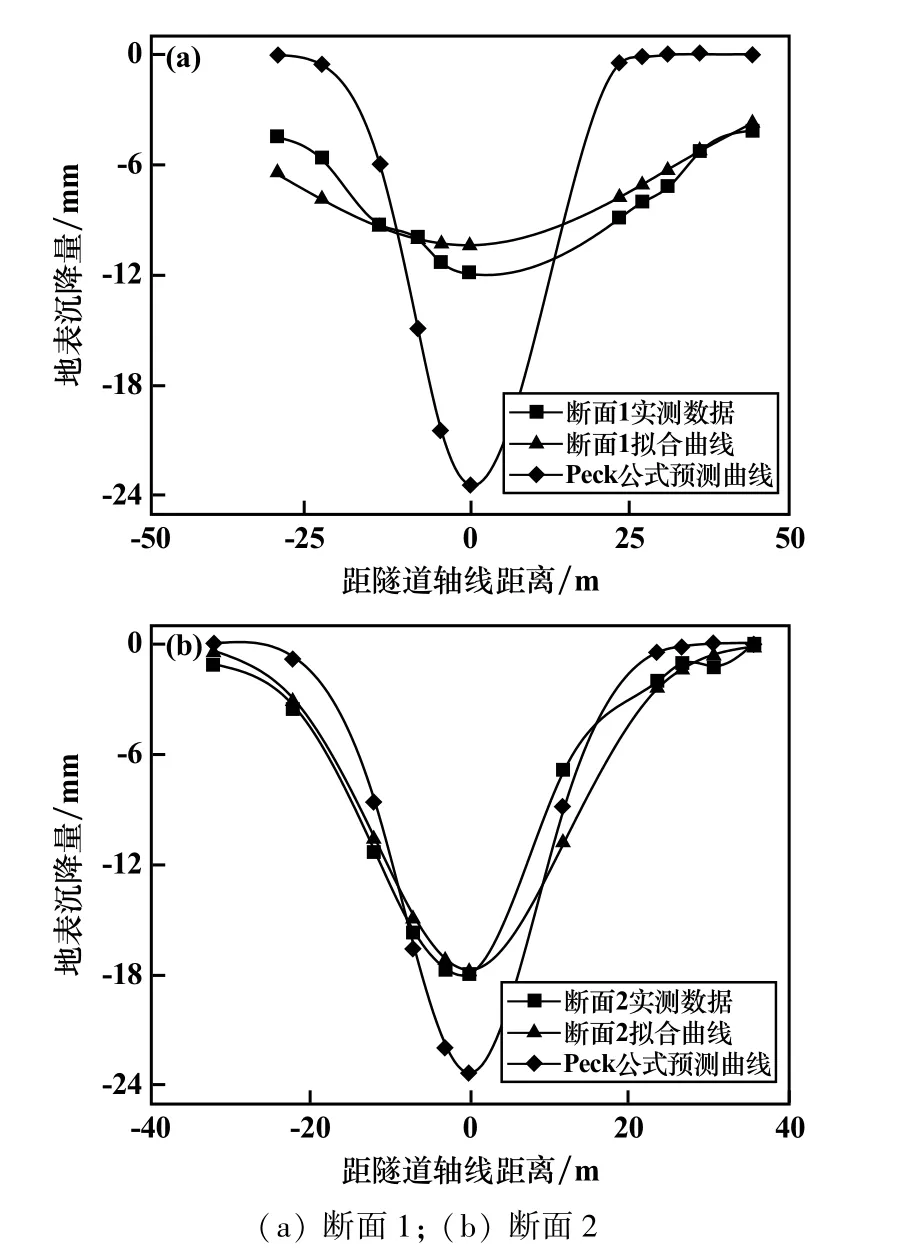
图7 各断面实测曲线、拟合曲线与Peck公式预测曲线对比
3 某过江隧道的Peck公式修正
传统Peck经验公式与线性回归拟合曲线形态分布大体一致,但沉降峰值与沉降槽宽度偏差较大。影响沉降峰值与沉降槽宽度的主要因素为Smax与i,故引入最大地表沉降修正系数修正因子α与沉降槽宽度修正系数β。
3.1 Peck公式修正
引入修正因子α与β,进行回归:
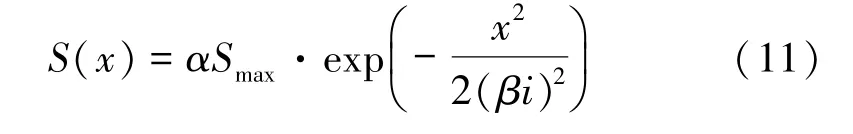
对式(11)进行线性变换,得:
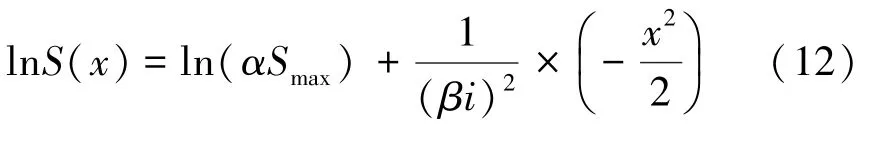
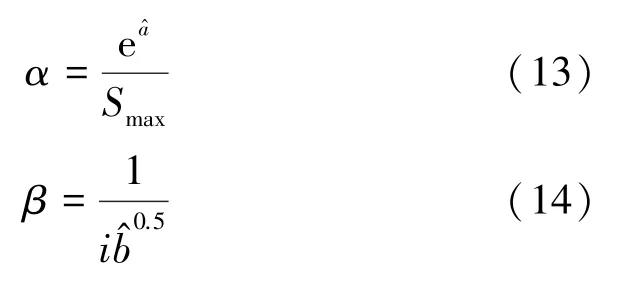
将上述2个断面的计算数据代入式(13)及式(14),可得断面1:α=0.44,β=3.64;断面2:α=0.76,β=1.39。
2断面的修正Peck公式为:
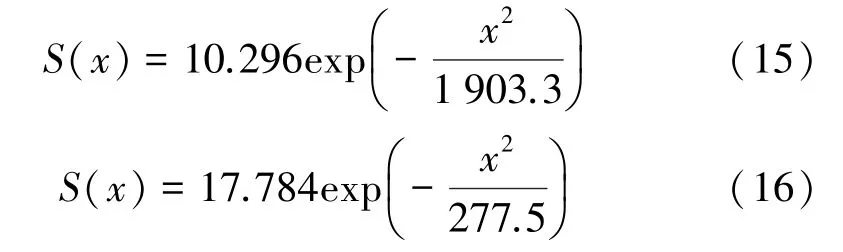
对比Peck修正曲线、拟合曲线、实测沉降数据(见图8),可以看出,修正Peck公式预测曲线与拟合曲线较相符,表明修正后的Peck公式更适用于该地区上软下硬地层大直径盾构施工工况。
根据监测资料选取10个断面沉降数据,分析修正系数α与β,见表4。由表4可知,修正系数α与β分布范围为0.4~0.8及1.2~2.4。通过与工况1中修正系数的分布范围比较,发现相似地层中考虑不同盾构直径时,分布范围存在明显差异。如图9所示,超大直径盾构施工时,α与β的分布范围明显大于常规盾构施工,由此推断,与常规盾构施工相比,超大直径盾构施工产生的最大地表沉降相对较大、沉降槽较宽、影响范围大。
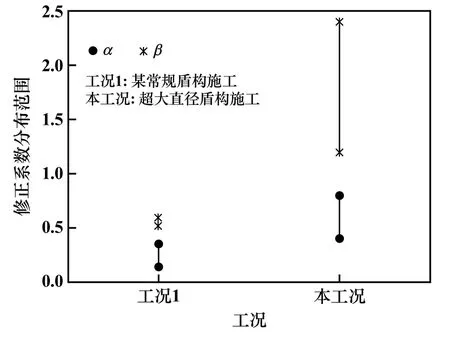
图9 不同工况修正系数范围
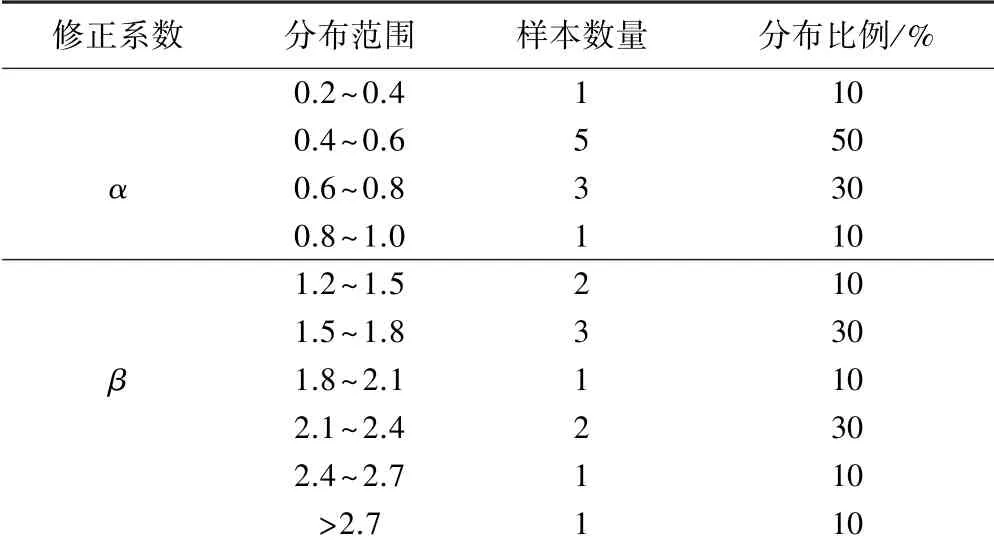
表4 修正系数分布
3.2 修正Peck公式的验证
为检验修正Peck公式能否准确预测上软下硬地层大盾构施工地表沉降,选取α上限值0.4、下限值0.8,β上限值1.2、下限值2.4,检验随机选取的4个断面实测地表沉降数据。图10为修正Peck公式预测曲线与实测地表沉降数据对比。
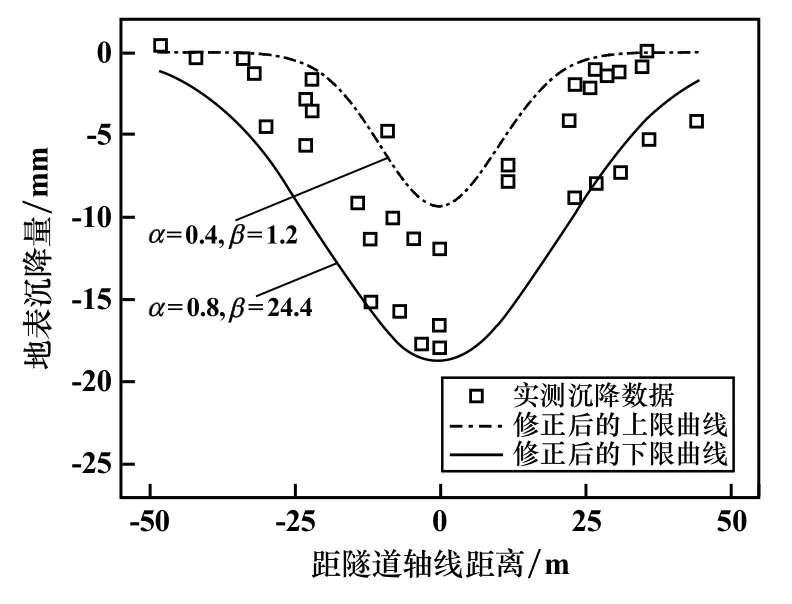
图10 修正Peck公式预测曲线与实测数据对比
可以看出,超过90%的实测数据分布于上限曲线和下限曲线之间,表明α和β取值合理,能得出地表沉降槽和最大沉降量变化范围,证实修正Peck公式适用于上软下硬地层大盾构施工引发的地表沉降预测。
4 结 语
1)上软下硬地层中,盾构施工引起横向地表沉降槽呈近似正态分布,开挖断面中心线处沉降最大,累计沉降量随距隧道中心线距离增加而减小。超大直径盾构在上软下硬地层施工引起地表沉降较大、沉降槽较宽、影响范围大。
2)随着盾构机穿越隧道断面,地表沉降逐渐增加,隧道轴线处的地表沉降速率明显大于两侧。盾构机穿越断面阶段引发的地表沉降占累计沉降量的62.8%。注浆完成后,地表趋于稳定,但沉降仍不可忽略。
3)引入最大地表沉降修正系数α与沉降槽宽度修正系数β修正Peck公式,修正系数α与β取值分别为0.4~0.8以及1.2~2.4时,修正Peck公式预测精度较高,适用于上软下硬地层大直径盾构施工地表沉降预测。
