综合考虑车道划分和流量分布的交叉口相位结构优选方法

荆彬彬 姜致远 夏有萌 沈莉婷 章 强 林 葳

(南通大学交通与土木工程学院 南通 226019)

0 引 言

平面信号交叉口是城市路网通行能力的瓶颈，是交通拥堵的关键节点.科学合理的信号优化控制可以提升交叉口通行能力、缓解交叉口拥堵.根据优化指标的不同，交叉口信号控制研究成果可分为单一性指标优化和多元性指标优化.在单一性指标优化中，主要针对平均延误时间[1-2]、车辆排队长度[3-4]等.在多元性指标优化中，优化指标的类型比较多样，如综合延误时间和停车次数[5-6]，综合延误时间、停车次数，以及排队长度[7-8].除了上述传统优化指标外，车辆尾气排放作为优化指标也纳入交叉口信号配时模型中[9-10].近年来，车联网环境下的单交叉口信号控制问题成为研究的热点，部分学者提出了自动驾驶环境下的交叉口信号控制策略，能够有效提升交叉口通行效率.

现有单交叉口信号配时理论主要聚焦在信号配时参数(如信号周期、绿信比等)与交通运行指标(如延误时间、停车次数、排队长度、车辆排放等)之间定量关系的研究上，其研究思路多是在给定的相位结构(如对称相位、搭接相位或单独相位)下探究配时参数与运行指标之间存在的定量数学关系，对交叉口相位结构优选方面的研究涉及较少，即如何从多个备选相位结构中选取出最佳相位结构.而相位结构的合理选择却是设计交叉口信号方案时所面临的首要任务，这是因为相位结构决定着后续关键车流的判断、总损失时间以及总流量比的计算等.基于此，文中综合考虑交叉口进口道车道功能划分和流量方向分布，给出一套面向关键车流总流量比最小的相位结构优选流程.针对两种典型的车道功能划分情况，给出了相位结构优选流程中关键车流总流量比的计算方法，并以南通市园林路与洪江路交叉口为例验证了所提相位结构优选方法的有效性.

1 相位结构优选方法

在满足通行能力的前提下，交叉口宜采用较短的周期时长，这样整个交叉口的运转效率会显著提升，延误时间、排队长度会相应减小.基于该思路，本研究以关键车流总流量比最小(可等价于周期时长最小)作为相位结构优选目标，优选流程见图1.

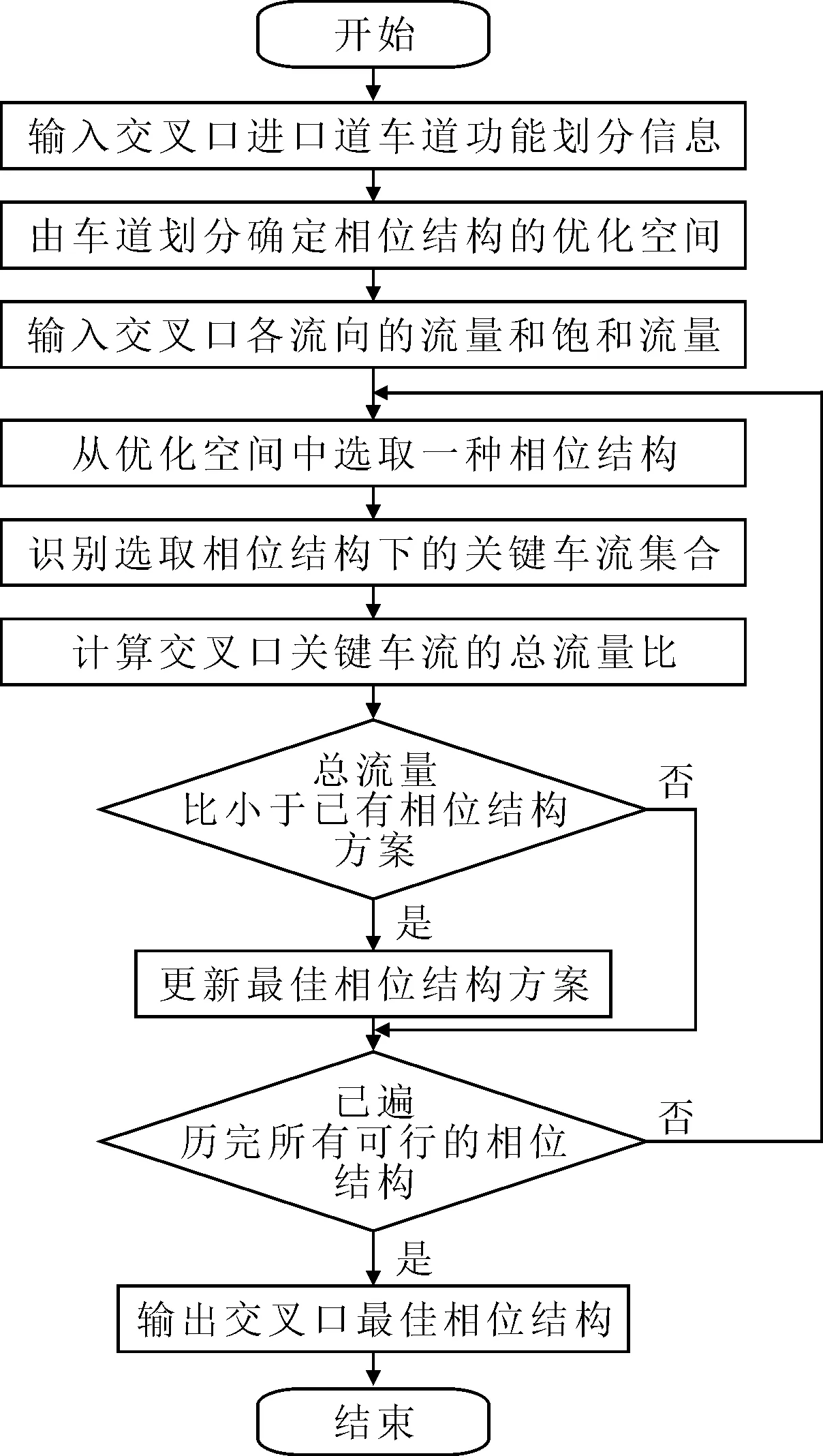
图1 相位结构优选流程

由图1可知：关键车流总流量比的计算是整个优选流程中最为关键的环节.下面结合典型进口道车道功能划分情况，给出关键车流总流量比的计算方法.关键车流流量比等于关键车流的交通量或设计交通量(高峰小时最高15 min的流率×4)与其饱和流量的比值.

当交叉口进口道左转、直行均为专用车道(见图2)时，此时该车道功能划分记为情况I.

图2 车道划分情况I

车道功能划分情况I对相位结构没有特定要求，情况I下相位结构的优化空间为：对称相位、搭接相位、单独相位.

1) 车道划分情况I下相位结构为对称相位时(见图3)，关键车流总流量比Y为

Y=max{y1,y2}+max{y3,y4}+

max{y5,y6}+max{y7,y8}

(1)

式中：y1～y8分别为车流1～8的流量比；max{y1,y2}为从车流1和2中选择流量比最大的车流作为关键车流，其他同理分析.

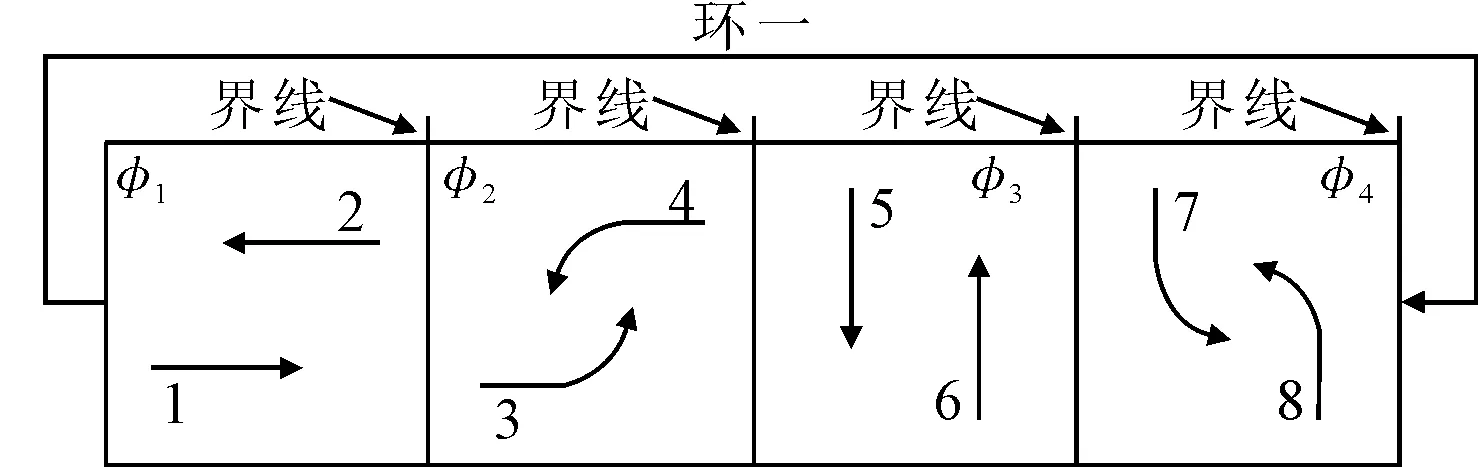
图3 对称相位结构

2) 车道划分情况I下相位结构为搭接相位时(见图4)，关键车流总流量比Y为

Y=max{y1+y4,y2+y3}+

max{y5+y8,y6+y7}

(2)

图4 搭接相位结构

3) 车道划分情况I下相位结构为单独相位时(见图5)，关键车流总流量比Y为

Y=max{y1,y3}+max{y2,y4}+

max{y5,y7}+max{y6,y8}

(3)

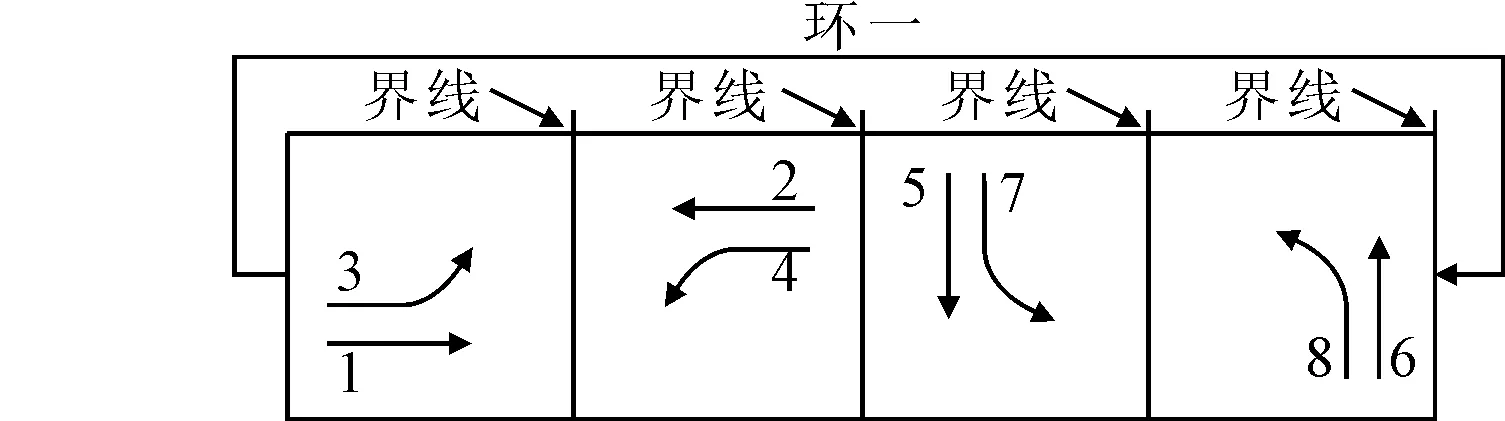
图5 单独相位结构

图3～5中的界线表示当相位运行到该界线时该相位内的车流其通行权必须同时停止，然后切换到下一相位.对于图4的搭接相位中车流1和车流3是可以共用绿灯时间的，同理车流2和4、车流5和7、车流6和8.也就是说，对于南北方向或东西方向而言，图4的搭接相位是各有四种相序模式的，而图1的对称相位是只有一种相序模式.

当交叉口进口道存在左转和直行共用一条车道见图6时，此时车道划分记为情况II.

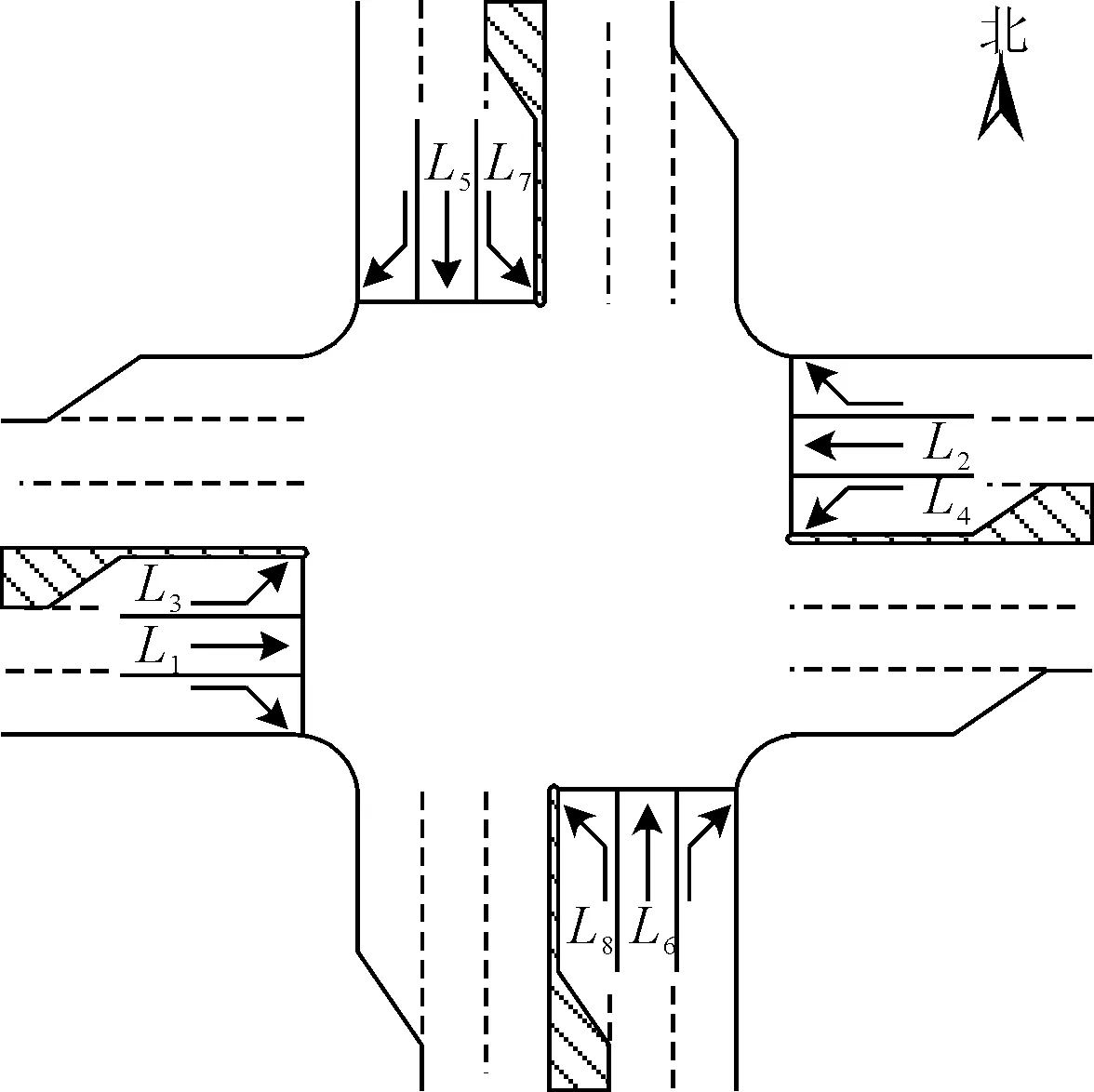
图6 车道划分情况II

车道划分情况II对相位结构有特定要求，仅能选择单独相位.原因在于：由于存在直左共用车道，采用对称相位或搭接相位时会出现直左车道上直行和左转车辆相互阻碍通行的情况.车道划分情况II下关键车流总流量比为

Y=yW+yE+yS+yN

(4)

式中：yW、yE、yS、yN分别为西进口、东进口、南进口、北进口直行车道组的流量比.

当交叉口各进口道车道功能划分为上述两种典型情况的组合或者采用其他特殊布置(如左转车道位于直行车道外侧)时，可根据车流之间是否存在冲突这一原则确定相位结构的优化空间.

2 实例分析

2.1 交叉口基本参数

以南通市园林路与洪江路交叉口为例验证所提相位结构优选方法的有效性与实用性.该交叉口的几何布局见图7.洪江路上方的高架将其地面道路分隔成了两部分(记为主路和辅路，二者之间存在绿化带，进口道处无法进行车道变换).道路中央绿化带处提供安全岛可供行人二次过街.

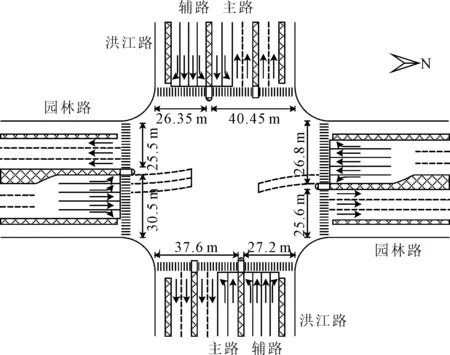
图7 园林路与洪江路交叉口几何布局

选择工作日晚高峰时段(17:30—18:30)调查该交叉口交通流量的方向性分布.各进口道各流向的设计交通量根据该高峰小时中最高15 min的流率进行计算，结果见图8.图8中每股交通流对应两个流量数值，小括号中的数值为该流向车流高峰小时中最高15 min的流量，中括号中的数值表示该流向车流的设计交通量.

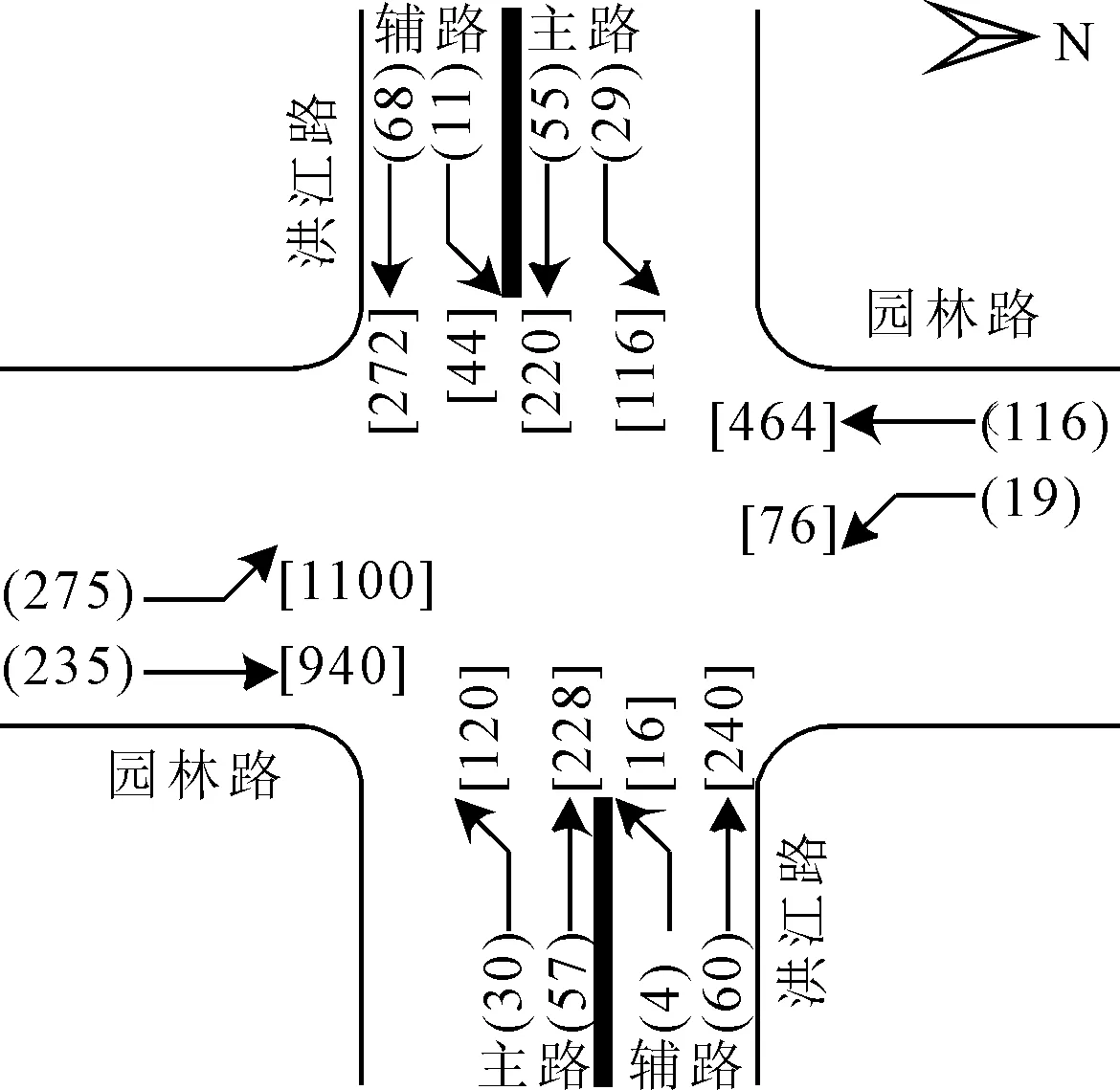
图8 各车流的最高15 min流率和设计交通量

2.2 流量比计算

计算各流向车流的流量比，其数值等于设计交通量与饱和流量的比值.这里直行车道、左转车道的基本饱和流量分别为1 650，1 550 pch/h[11].根据文献[11]，考虑车道宽度的影响对饱和流量进行修正.综上，各流向车流的流量比见图9.

图9 各流向车流的流量比

1～12-车流编号；小数-车流的流量比.

2.3 相位结构优选

1) 东西方向上相位结构优选 根据图1交叉口相位结构优选流程，首先确定园林路与洪江路交叉口东西方向上的相位结构优化空间.根据东西进口道车道功能划分情况，可知东西进口道上存在左转车道位于直行车道外侧的情形.因此，该交叉口东西方向上只能采用对称相位结构.东西直行相位中关键车流为东进口主路直行车流(流量比为0.121 21)，东西左转相位中关键车流为东进口主路左转车流(流量比为0.067 91).因此，东西方向关键车流的总流量比为0.189 12.

2) 南北方向上相位结构优选 根据南北方向进口道车道功能划分情况，可知该车道功能划分属于情况I.因此，该交叉口南北方向上相位结构的优化空间为对称相位、搭接相位、单独相位.根据关键车流总流量比的计算方法，计算对称相位、搭接相位、单独相位下的关键车流总流量比分别为0.639 69、0.448 58、0.448 58.根据关键车流总流量比最小的优化目标，因此该交叉口南北方向上最佳相位结构为搭接相位或单独相位.

2.4 优选相位结构评价

利用经典交叉口信号配时理论即Webster理论，分别计算最佳相位结构(南北方向为搭接相位或单独相位)、非最佳相位结构(南北方向为对称相位)下的信号配时方案.假定每股关键车流的损失时间为3 s，黄灯时间取值3 s，无全红灯时间.Webster信号周期计算见式(5).总绿信比按照等饱和度原则进行分配.

(5)

式中：L为关键车流总损失时间；Y为关键车流总流量比.

下面从仅考虑机动车通行需求、综合考虑机动车和行人过街通行需求两个层面分别设计信号配时方案.同时，机动车最小绿灯时间一般不应小于15 s.行人过街最小绿灯时间的计算见式(6).当绿灯时间不满足上述要求，需要对其进行调整.

(6)

式中：dp为行人过街的长度，m；vp为行人过街的速度，一般取值1.2 m/s；I为绿灯时间间隔(黄灯时间与全红时间之和)，s.

1) 仅考虑机动车通行需求

①南北为搭接相位、东西为对称相位 南北方向最佳相位结构为搭接相位，东西方向为对称相位时，仅考虑机动车通行需求的信号配时方案见图10(记为信号配时方案I).

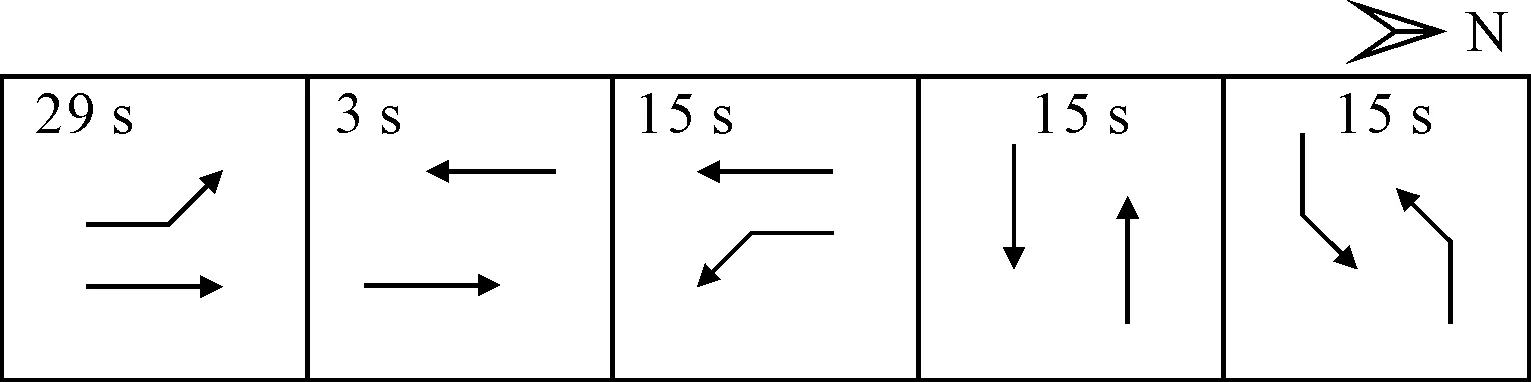
图10 信号配时方案I

②南北为单独相位、东西为对称相位 南北方向最佳相位结构为单独相位，东西方向为对称相位时，仅考虑机动车通行需求的信号配时方案见图11(记为信号配时方案II).

图11 信号配时方案II

③南北为对称相位、东西为对称相位 南北方向为对称相位(非最佳相位结构)，东西方向为对称相位时，仅考虑机动车通行需求的信号配时方案见图12(记为信号配时方案III).

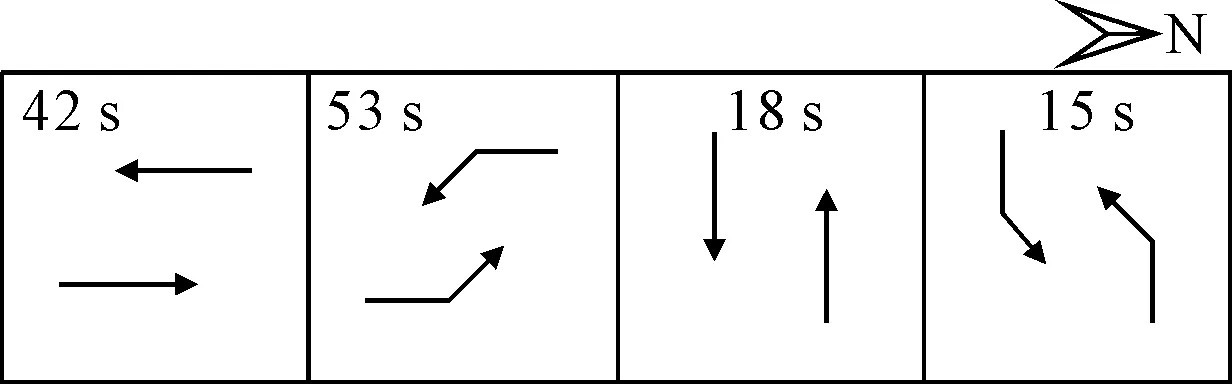
图12 信号配时方案III

2) 综合考虑机动车和行人过街通行需求 根据式(6)以及图7该交叉口几何布局情况，可确定东进口道行人过街最小绿灯时间为36 s，西进口道行人过街最小绿灯时间为38 s，南进口道行人过街最小绿灯时间为30 s，北进口道行人过街最小绿灯时间为27 s.

①南北为搭接相位、东西为对称相位 南北方向最佳相位结构为搭接相位，东西方向为对称相位时，综合考虑机动车和行人过街通行需求的信号配时方案见图13(记为信号配时方案IV).

图13 信号配时方案IV

②南北为单独相位、东西为对称相位 南北方向最佳相位结构为单独相位，东西方向为对称相位时，综合考虑机动车和行人过街通行需求的信号配时方案见图14(记为信号配时方案V).

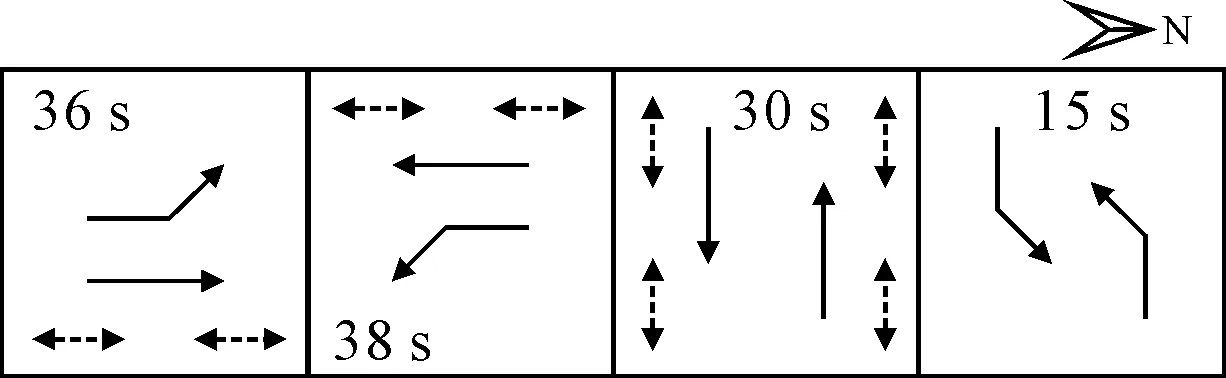
图14 信号配时方案V

③南北为对称相位、东西为对称相位 南北方向为对称相位(非最佳相位结构)，东西方向对称相位时，综合考虑机动车和行人过街通行需求的信号配时方案见图15(记为信号配时方案VI)

图15 信号配时方案VI

可以看出，仅考虑机动车通行需求时，采用最佳相位结构时信号配时方案I和II的周期时长分别为89和86 s；采用非最佳相位结构时信号配时方案Ⅲ的周期时长为140 s.

同样可以看出，综合考虑机动车和行人过街通行需求时，采用最佳相位结构时信号配时方案IV和V的周期时长分别为124和131 s；采用非最佳相位结构时信号配时方案VI的周期时长为152 s.

综上所述，无论是仅考虑机动车通行需求还是综合考虑机动车和行人过街通行需求，采用本文所提方法优选出的最佳相位结构可以获得更小的周期时长，而更小的周期时长可确保交叉口运行效率更快、车辆延误时间和排队长度更小，从而说明本文所提相位结构优选方法是有效的.

从关键车流总流量比最小来说，搭接相位和单独相位均是南北方向上的最佳相位结构，然而南北方向为搭接相位时计算出的周期时长和单独相位时计算出的周期时长是不同的，原因在于考虑到机动车、行人过街最小绿灯时间需求，对绿灯时间进行了调整.

2.5 与现有信号方案对比

该交叉口在调查时段运行的信号配时方案见图16.由图16可知，该交叉口信号方案是基于对称相位结构设计的.图16为各车流的绿灯时间，其黄灯时间均为3 s，该交叉口调查时段实际运行信号周期时长为120 s.

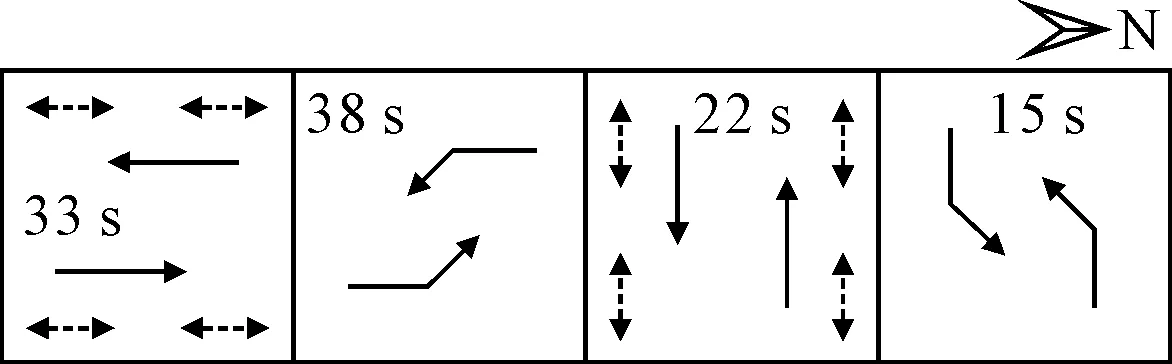
图16 该交叉口实际运行信号方案

1) 从安全的角度对比分析 根据上文行人过街所需要的最小绿灯时间数据可知，该交叉口在调查时段实际运行的信号配时方案是无法满足行人安全过街需求的，这将给行人过街带来极大的安全隐患，极易导致安全事故.利用本文所提的相位结构优选方法设计出的信号配时方案可以满足行人安全过街的需求，降低了安全隐患.因此，从安全的角度来看，本文所提的相位结构优选方法更为有效.

2) 从效率的角度对比分析 根据上文相位结构优选以及信号配时设计结果，仅考虑机动车通行需求时，南北方向最佳相位结构为搭接相位时设计出的信号配时方案中周期时长为89 s；南北方向最佳相位结构为单独相位时设计出的信号配时方案中周期时长为86 s.相比于该交叉口实际运行的120 s周期时长，采用本文所提方法优选出的最佳相位结构可以获得更小的周期时长，能够有效提升交叉口运转效率.

综合考虑机动车和行人过街通行需求时，南北方向最佳相位结构为搭接相位时设计出的信号配时方案中周期时长为124 s；南北方向最佳相位结构为单独相位时设计出的信号配时方案中周期时长为131 s.然而，该交叉口实际运行的信号方案是无法同时满足机动车和行人过街通行需求的，若要满足该要求，基于该交叉口实际运行的相位结构即对称相位，则需要将其信号方案调整至图15的方案，调整后周期时长则变为152 s.可以看出，相比于调整后152 s的周期时长，本文所提方法优选出的最佳相位结构对应的周期时长是更小的(南北方向最佳相位结构为搭接相位和单独相位时，分别对应的周期时长为124和131 s)，因此可以获得更好的运行效率.

因此，综合考虑安全和效率两个因素，本文所提的相位结构优选方法是有效且实用的.

3 结 束 语

针对交叉口相位结构选取问题，本文提出了一种面向关键车流总流量比最小的相位结构优选方法，并以实际交叉口为例验证了所提方法的有效性与实用性，为解决交叉口相位结构优选问题提供了理论依据和实用参考.

然而，本文所提的相位结构优选方法还存在以下问题需要进一步研究：①当优选出的最佳相位结构存在多个时，如何再进一步优选，可结合行人过街时间需求等因素进行系统研究(本文仅在实例中对此进行了简单讨论)；②对关键车流的判断是以流量比大小为依据的，后期可综合考虑车流损失时间、饱和度限值等因素综合判断；③所提方法仅适用于单交叉口，后续可重点关注干道、路网信号协调时的相位结构优选问题即交叉口相位结构与协调控制参数的协同优化.