数据驱动的城市路网短时交通流预测

唐进君 曾 捷 段一鑫

(中南大学交通运输工程学院 长沙 410075)

0 引 言

交通流预测的对象包括流量、速度、占有率，以及行程时间等交通参数.按照数据采样间隔及预测时长来划分，可分为长期预测与短时预测两种类型.其中，短时交通流预测的数据采样及预测步长主要为2，5，10 min等；而长期交通流预测普遍按照h、d、月及更长间隔等作为采样间隔来统计交通流数据，进而预测其未来变化情况.短时交通流预测是ITS中诸多实时应用的基础，能够在缓解交通拥堵、动态路径规划，以及信号配时优化等方面发挥重要作用.

根据所预测的道路类型来进行分类，短时交通流预测可以分为高速公路交通流预测和城市道路交通流预测两种类型.其中，相较于高速公路交通流预测而言，城市道路交通流所服务的出行者范围更广，路网中各路段之间的连通性更强，交通状态检测设备更为丰富，因此在交管部门的实时管理中具有广阔的应用前景.同时，由于城市路网中存在着信号设备的固定控制，会对交通流产生周期性的间断作用，导致其在短时内具有更为强烈的波动性，从而给准确的短时预测带来了极大的挑战.

本文立足于大数据背景下的城市道路交通流预测，根据预测对象的空间维度将现有研究划分为单节点交通流预测及路网级交通流预测，研究范围涵盖统计学模型、机器学习模型、传统深度学习模型及新颖的图神经网络模型.基于现有预测方法及预测模式，总结了现有研究中存在的不足，并指出了未来的研究热点及进展.

1 研究现状

1.1 单节点交通流预测

将路段、检测器等交通流状态采集地点定义为路网中的节点.单节点交通流预测是指基于单个节点(即路段或检测器)或其周围多个节点的历史交通流信息来预测单个节点的未来交通状态.其中，又可以根据所使用到的周围节点的数量来将这种预测模式进一步划分为：考虑交通流时变特征的预测方法与考虑空间相关性的预测方法.前者仅使用到了目标节点的历史交通流数据，而后者则引入了与目标节点具有较强相关性(包括相关性系数以及上下游影响等)的节点的历史交通数据.

1.1.1考虑交通流时变特征的预测方法

交通状态的时间关联性是交通流预测中最为重要的影响因素之一.图1以长沙市某交叉路口2019年7月期间交通流数据为例，进行交通流周期相似性分析.从时间维度来看，交通流的时间关联性包括短时相关性、日相似性、周相似性等.为了充分挖掘交通流的时变特征，学者们广泛应用统计学方法、机器学习方法及部分深度学习方法(主要为循环神经网络及其变体)来探索交通流的时间相关性.

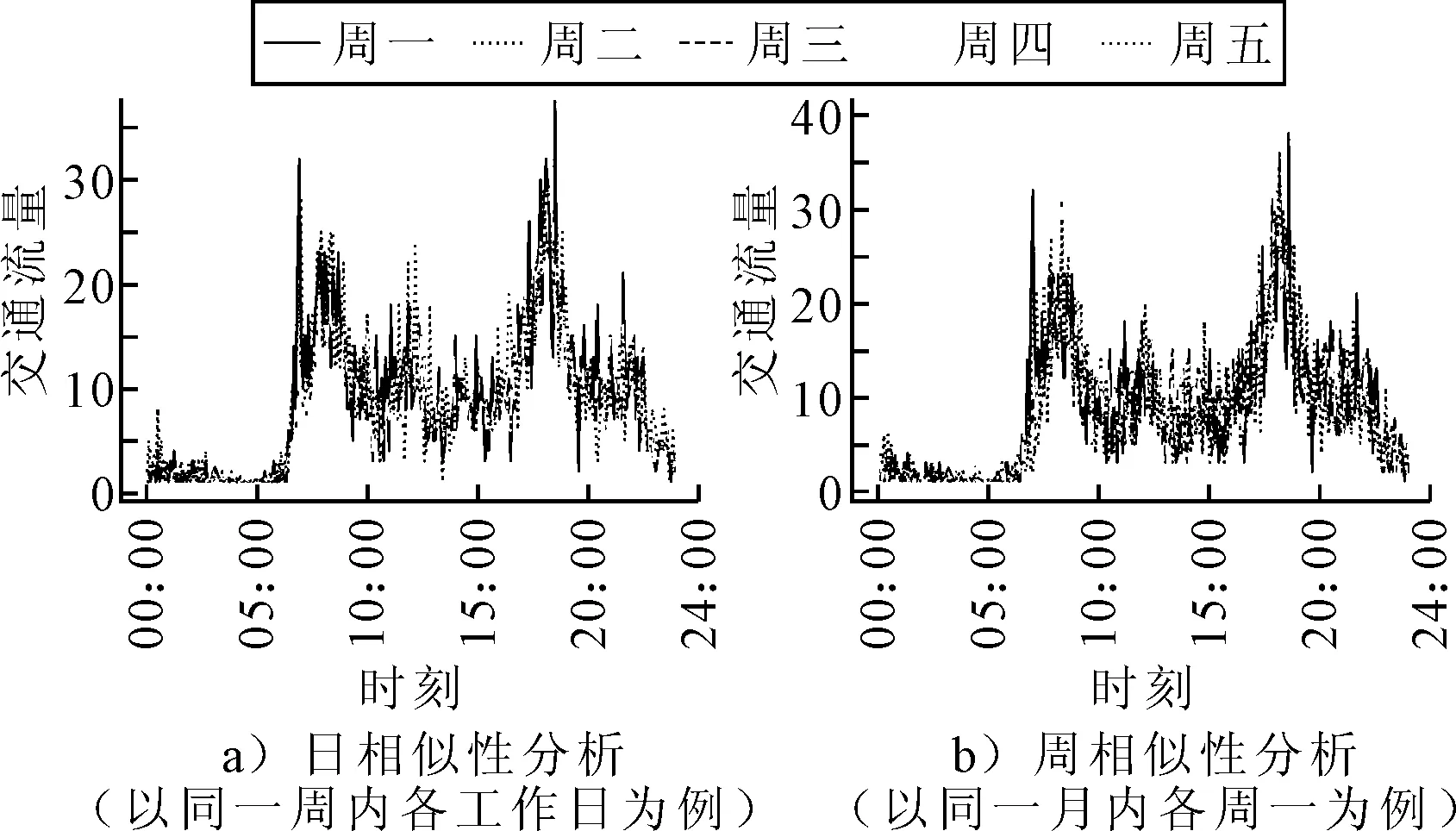
图1 交通流时变特征分析

当仅考虑交通流时变特征时，预测模式可以概括为：假设xt={xt-p+1,xt-p+2,…,xt}为t时刻的输入向量；xt为t时刻的交通流数据，旨在从历史数据库中学习或计算得到一个映射函数F(·)，从而能够预测得到t+q时刻的交通流参数.

(1)

1) 基于统计学的预测方法 统计学方法通常将单个节点的交通流数据视为序列数据，从而使用时间序列分析方法进行预测.在所有的统计学方法，差分整合移动平均自回归模型(autoregressive integrated moving average, ARIMA)及其变体是短时交通流预测领域中应用最为广泛的时间序列分析方法.同时，其他的时间序列分析模型，如卡尔曼滤波(Kalman-filter)、广义自回归条件异方差模型(generalized autoregressive conditional heteroskedasticity model, GRACH)等，也都在这一领域中得到了广泛的应用.韩超等[1]基于ARIMA模型提出了一种自适应预测算法，在仿真数据上的预测结果表明:该模型在不同的交通流状态下均能取得较为准确的预测效果.李文勇等[2]提出了一种结合Box-Cox指数变换与ARIMA的改进模型，能够有效解决由交通流的长期自相关所产生的异方差性.薛洁妮等[3]提出了一种基于混沌时间序列分析方法的短时交通流预测模型，通过相空间重构、局部多项式拟合等操作来实现准确预测.实验结果表明：该方法既能够保证一定的预测准确性，同时还能满足实时应用的需求.Min等[4]将时空ARIMA模型与动态转向率预测模型相结合，设计了一种名为动态时空ARIMA的预测框架，用于提升城市交叉口处交通流预测的准确性与预测效率.Li等[5]提出了一种基于偏最小二乘回归(partial least square, PLS)的预测模型，该模型能够有效兼顾预测准确性与运算效率，并且具有较强的可解释性.

然而，虽然这些基于统计学方法的预测模型能够给短时交通流预测任务带来更强的可解释性，但是往往在探索交通时序数据的复杂非线性关系中具有局限性，并且存在着计算复杂度高的缺点.在如今大数据时代的交通系统中，难以取得较好的预测效果.

2) 基于机器学习的预测方法 为了缓解这些基于统计学模型中所存在的不足，将机器学习模型用于短时交通流预测研究，模型包括人工神经网络(artificial neural networks, ANN)、支持向量机(support vector machines, SVM)、决策树(decision trees)及贝叶斯网络(Bayesian networks)等.Tang等[6]在充分考虑交通流时间序列的周期性特征的基础上，通过将无监督学习与监督学习相结合的方式，提出了一种改进的模糊神经网络(fuzzy neural network, FNN)结构，用于城市道路短时速度预测.此后，考虑到交通流时间序列的波动性，Tang等[7]引入了一种数据降噪方法来缓解交通流的波动性，并将降噪结果输入SVM模型来实现准确预测.同时，为了进一步提升机器学习模型的预测效果，避免模型参数在训练过程中陷入局部最优解，大量的学者引入了启发式算法来优化机器学习模型的有关参数.姚智胜[8]提出了一种基于最小二乘支持向量机回归算法的短时交通流预测模型，并将遗传算法与回溯系数选择过程相结合用于模型最佳参数选择.李松等[9]在BP神经网络的基础上引入了一种改进粒子群算法，从而利用粒子群算法来对于神经网络中的权重进行优化，有助于提升模型的预测准确性.

在传统的机器学习模型中，普遍缺乏能够有效处理时间序列数据的模块，从而导致其对时间序列特征的学习能力存在不足.同时，机器学习模型往往需要在数据预处理阶段人为设定一系列特征工程，而非直接通过模型对于数据特征进行挖掘.因此，当面临体量庞大且多源异构的交通流数据时，传统的机器学习模型难以取得满意的预测效果.

3) 基于深度学习的预测方法 应用于短时交通流时变特征挖掘及预测领域的深度学习模型主要为循环神经网络(recurrent neural network, RNN)及其变体长短时记忆网络(long short-term memory, LSTM)和门控循环单元(gated recurrent unit, GRU).LSTM是目前RNN及其变体中应用最为广泛的模型，其模型结构见图2.该模型的主要组成部分包括：输入门(input gate)、遗忘门(forget gate)、输出门(output gate)及记忆单元(memory cell).在模型的计算过程中，能够利用输入门来获取当前时刻的交通状态，并且通过遗忘门来保留历史交通信息，从而提升了模型处理时间序列的能力.

图2 LSTM模型结构图

Ma等[10]首次将LSTM应用于短时交通流预测领域，实验结果证明了LSTM能够取得明显优于传统的机器学习模型以及统计学模型的预测效果.Ma等[11]提出了一种结合时间序列分析方法与LSTM-双向LSTM的短时交通流预测方法.实验结果表明：相较于基础的LSTM模型及双向LSTM模型而言，该组合模型能够在预测稳定性和准确性上均取得一定的提升.Gu等[12]利用贝叶斯方法设计了一种由GRU、ARIMA，以及径向基网络组成的预测框架，从而能够在面临不同交通状态时使用更为合适的模型进行预测.Peng等[13]构建了一种结合注意力机制与LSTM的ALSTM模型结构，实验结果表明：所使用到的注意力机制能够有效提升LSTM对时间序列特征的学习能力.陆文琦等[14]在利用集成经验模态分解(empirical mode decomposition, EMD)方法处理原始交通速度数据的基础上，设计了一种结合双向LSTM及注意力机制的混合深度学习模型，实现了车道级交通速度的准确预测.张炜健[15]立足于轨迹数据分析，利用EMD算法处理高频噪声数据，并利用GRU模型实现交叉口处转向流量预测.但是，在路网中行驶的车辆总是会在一定时间内连续通过若干个路段，因此会给路网中不同位置的交通状态之间带来空间关联性.然而，在这些基于RNN及其变体的交通流预测模型中，往往忽略了不同空间位置的交通流之间的交互性.因此，其预测效果往往受到限制，并且容易在多步预测任务中产生较大的预测误差.

1.1.2考虑空间相关性的预测方法

(2)

从预测原理上看，开展相关联节点的有效识别是此类预测方法的关键.根据节点相关性度量的原理，可以将现有研究划分为经验定义方法以及数据驱动方法两大类.

经验定义方法可以总结为：根据各节点在路网中的上下游关系，来确定各节点之间的关联性，该方法的示意图见图3.Yao等[16]提出了一种基于时间参数与空间参数的SVM模型，用于城市道路的短时速度预测研究.刘晓玲等[17]的研究表明，SVM模型在同时考虑目标路段及其下游路段的交通状态时，能够在短时交通流预测任务中取得更为准确的预测效果.韩卫国等[18]在利用时空ARIMA模型进行短时交通流预测的过程中发现，当同时引入目标交叉口以及其相邻交叉口的交通流时间序列数据时，模型的预测准确性能够取得大幅提升.王祥雪等[19]通过运用交通流时空关联性开展了交通流时间序列重构，并提出了一种结合LSTM与RNN的深度学习模型，用于城市快速路短时交通流预测.杨春霞等[20]设计了一种融合上下游关系与LSTM的短时交通流预测模型，并提出了一种基于岭回归算法的权重计算方法，从而得到最终的预测值.

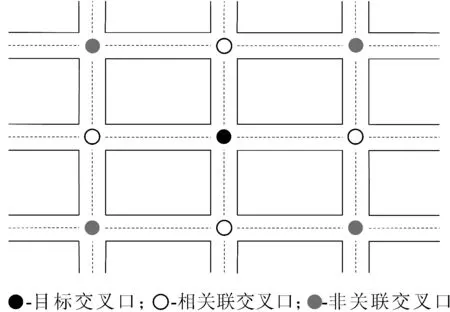
图3 基于上、下游邻接关系的相关联交叉口识别示意图

而数据驱动的方法的原理可以概括为：基于历史交通流数据库，利用相关系数等方法来定量刻画节点之间的关联性，进而为目标节点选取关联性最强的若干个节点.Li等[21]设计了一种基于贝叶斯网络的交通流预测框架，并选取了Graphical Lasso方法、空间邻近准则以及相关系数方法来进行关联路段选取.Gu等[22]在城市道路车道级速度预测中引入了灰色关联分析来识别出与目标车道关联性较强的车道，并设计了一种结合LSTM与GRU的堆叠模型开展短时速度预测.Tang等[23]通过融合交通流时间序列的统计学相关性以及路网交通特征，进行相关联的交叉口进口道识别，并引入了一种结合遗传算法与LSTM的GA-LSTM模型来开展进口道级短时流量预测.

大量研究表明:引入空间关联性的模型能够取得更为准确的预测效果.但是，由于其往往仅用于预测单个节点的未来交通状态，因此难以在短时内为交通网络的实时应用管理提供足够的有效信息.同时，考虑到此类预测模型需要针对于每个节点分别进行模型训练，因此当路网规模扩大时，模型的训练开销与存储开销会呈现线性上升的趋势，导致其实用性大幅下降.

1.2 路网级交通流预测

1.2.1基于卷积神经网络的预测方法

由于卷积神经网络(convolutional neural network, CNN)能够有效挖掘图片中各像素点之间的关联性，因此已有大量学者将其引入路网级交通流预测研究中.同时，一些特殊的CNN结构，如Conv1D、时间卷积网络(temporal convolutional network, TCN)等，也能够被直接用于单点交通流预测中.一般而言，基于CNN的交通流预测方法首先需要构建栅格结构的历史交通流数据，进而利用CNN来挖掘各栅格之间的时空关联性.在现有短时交通流预测研究中，栅格构建方法可以分为三种类型.

1) 将栅格化处理以后的城区视为图片，具体构建方法见图4.蒲悦逸等[24]设计了一种基于端到端(End to End)框架的交通流预测模型，在对城市区域进行栅格化处理的基础上，分别利用ResNet以及LSTM探索交通流的时空关联性，并通过实例分析证明了该模型不仅能够取得更为准确的预测效果，还能够有效减少模型参数.Zheng等[25]将厦门市进行规则网格划分，并提出了一种名为DeepSTD的端到端学习框架来进行全市范围内的交通流预测.Zhang等[26]在将城区进行网格划分的基础上，设计了一种名为ST-ResNet的预测模型，来对于各区域的进、出交通量进行预测.在此基础上，Zhang等[27]进一步考虑了区域内部交通量与区域间OD交通量的协同性，构建了一个多任务深度学习模型来实现二者的协同预测.Liu等[28]基于ConvLSTM模型构建了一种名为Attentive Traffic Flow Machine的交通状态预测模型，其中所使用到的ConvLSTM是一种结合CNN与LSTM运算机制的混合模型，能够有效提取栅格化数据的时变特征.

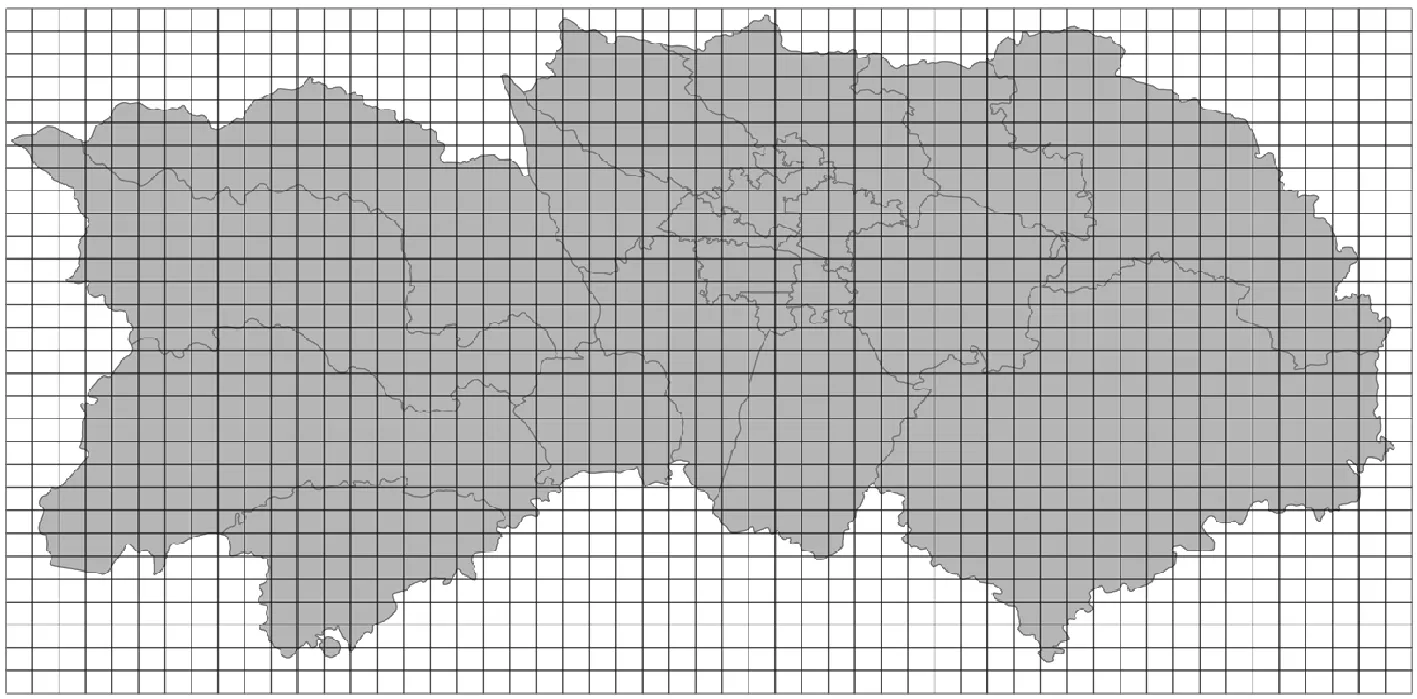
图4 基于栅格化处理的网格数据构建方法

2) 将路网中各节点按照一定的排列规律排列为二维空间矩阵形式，其构建示意图参见图5.Dai等[29]为了使用CNN在高速公路网络上开展短时交通流预测，提出了一种检测器排列算法，从而将高速公路网络中的各检测器按照一定的规律排列为二维矩阵形式，便于使用CNN进行预测.

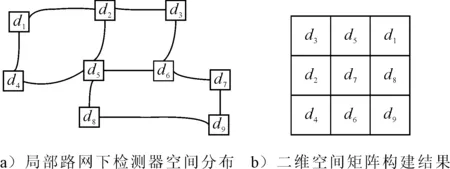
图5 检测器网络的二维空间矩阵转化过程示意图

3) 将由所有节点在同一时刻构成的交通流数据按照一定规则排列为向量，进而将各时刻的向量按照时间先后顺序堆叠为二维矩阵形式.其中，该矩阵的行(或列)表征节点数量，矩阵另一维度表示先前时间步的长度.Ma等[30]构建了一种二维时空速度矩阵，并设计了一种CNN模型用于提取网络级交通流数据中的时空关联性.陈思曲等[31]利用时空关系将交通速度数据转化为二维矩阵形式，并设计了深度CNN模型开展行程速度预测研究.此外，唐克双等[32]在构建二维行程速度矩阵的基础上，设计了一种基于Inception框架的CNN模型，用于城市快速路速度预测.

虽然基于CNN的预测方法已经吸引了大量学者的关注，但是这三种栅格化数据构建方法在实际应用的过程中也面临着一些需要解决的问题.例如，对于第一种构建方法而言，在栅格划分的过程中会面临一大难题，即栅格的大小设置.如果栅格过大，则难以获取得到精细化的城市交通状态；而一旦栅格尺寸过小，则可能产生大量的交通数据缺失的栅格，从而给准确预测带来挑战.而对于第二、三种构建方法而言，则需要设计出一种合适的排列规则，用于将节点排列为合理的一维向量或二维矩阵形式.同时，在这些基于网格划分的预测方法中，所使用到的CNN模型普遍难以处理非欧几里得空间数据，因此路网的拓扑结构往往遭到了忽视，导致难以深入地挖掘路网内部的空间关联性.

1.2.2基于图神经网络的预测方法

由于城市路网具有天然的拓扑结构，因此近几年来大量学者应用了图神经网络(graph neural network, GNN)来实现路网级预测.其中，使用最为广泛的预测模型为图卷积神经网络(graph convolutional network, GCN)，同时图注意力网络(graph attention network, GAT)以及GraphSAGE等模型也都得到了大量应用.基于GNN的预测模式可以概括为：假设Xt∈N×M(其中，N为路网中的节点数量，M为预测所使用到的先前时间步的长度)，在给定拓扑网络G=(V,E)的情况下(V为节点集；E为边集)，旨在从历史数据库中学习得到一个映射函数F(·)，从而能够预测得到t+q时刻的路网中所有节点的交通流参数N.

(3)

Zhao等[33]通过结合GCN与GRU，构建了一种名为T-GCN的图神经网络模型，能够有效处理图结构的时间序列数据.Zhang等[34]为了解决交通流多步预测这一难题，提出了一种名为AGC-Seq2Seq的图神经网络预测模型，通过融合Seq2Seq、GCN以及注意力机制来深入挖掘路网交通流的复杂时空相关性.Liu等[35]提出了一种考虑时空关联性的数据修复算法，用于填补路段上的缺失速度数据，并利用GraphSAGE模型来开展网络级交通速度预测.Tang等[36]设计了一种结合复杂网络理论中的社团检测算法与GCN的MC_STGCN模型，并将其应用于出租车出行需求预测，通过实验证明了引入社团检测算法的有效性.闫旭等[37]为提高城市交通态势的预测精度，将自由流动可达矩阵(free-flow reachable matrix)引入时空图卷积神经网络中，构建了一种改进的网络级交通流量预测模型.魏金泽[38]针对于交通数据样本缺失的问题，设计了一种基于迁移学习机制的时空图网络模型，分别利用GRU以及GCN捕捉交通系统的时空关联性，并利用注意力机制挖掘时空模态特征，实现了小样本条件下短时交通流的准确预测.奚桂锴[39]设计了一种名为时空语义图神经网络的时空预测模型，利用时序建模策略分别提取交通状态的时空依赖性，并通过消融实验证明了各模块的有效性.潘卫鹏等[40]设计了一种图注意力卷积网络，并通过真实数据集上的交通流预测实验证明了该模型能够准确提取路网交通流的时空关联性.陈孟等[41]针对于实时多模态时空数据的变化特征，设计了一种结合时空图卷积网络与卡尔曼滤波的预测模型，并开展了有效性与可信度评估，证明了该模型的准确性与鲁棒性.曾筠程等[42]设计了一种基于有向图卷积神经网络的交通预测模型，并在此基础上提出了拥堵产生点识别方法及管控策略，从而有效阻断交通拥堵在路网中的蔓延，提升道路网络的通行效率.但是，在将图神经网络用于交通流预测的过程中，存在一个关键性的问题，即需要先构建一个或若干个合理的拓扑路网.在图神经网络中所使用到的拓扑网络不仅会对预测结果产生较大的影响，同时其疏密程度还会直接影响深度学习模型的运行效率.在现有的高速公路的短时交通流预测研究中，学者们普遍采取了物理邻接关系或者基于距离的网络构建准则来进行拓扑网络构建.但是，相较于高速公路网络而言，城市路网具有更为稠密的网络密度以及更大的连通性.以图6所示的局部路网内的车道级流量预测为例，该区域共存在四个交叉口，16个进口道，64条车道.如果直接从车道之间的邻接关系来提取得到拓扑网络，则可能致使部分连接边之间的关联性较弱.此外，出于检测设备安装及运维成本的考虑，城市路网内部并非所有交叉口处均安装了检测设备，导致配备有检测设备的交叉口在路网内部的空间分布情况较为稀疏.如何在稀疏条件下利用邻接关系进行拓扑网络构建，同样也是一项艰巨的挑战.而如果直接采取基于距离的网络构建方法，则会面临着难以定义城市路网内部车道与车道之间的距离这一难题.

因此，如何在城市路网内部更加合理、有效地为图神经网络构建拓扑图已成为网络级短时交通流预测研究亟需解决的问题.在现阶段，已有部分学者针对于这一问题展开尝试.文献[43]为了在分布稀疏的车牌识别设备(license plate recognition, LPR)所构成的路网下开展车道级以及进口道级短时交通流预测研究，提出了一种基于数据驱动的路网重构方法.该研究将车道或进口道视为网络中的节点，先从LPR数据中提取得到了各节点之间的平均行程时间以及流量转移关系，在此基础上将各节点之间的平均行程时间视为节点之间的距离，引入了一种复杂网络构建方法将路网转化为有向图，并在此基础上利用流量转移关系计算网络中各条边上的权重，从而将其构建为加权有向图，最终输入图神经网络中进行预测.通过多种图神经网络在路网邻接网络及所构建的加权有向图上的预测结果对比，实验结果表明：所选取的若干种图神经网络模型均能够在所构建的加权有向图上取得更为准确的预测效果.此外，在地铁短时客流预测领域中，Liu等[44]分别利用地铁拓扑网络、站点间客流相似度，以及站间OD矩阵来进行拓扑图构建，并提出了一种适合于多图卷积的图神经网络模型来实现客流预测.这些基于数据驱动以及复杂网络的研究方法为未来此领域的研究提供了一种可行的思路，即可以利用路网交通特征来进行网络重构，而非直接使用路网内部的邻接关系.通过这种方式，不仅能够有效解决检测设备分布稀疏这一问题，同时还能够引入更为丰富的实际交通特征到拓扑网络构建的过程中来，有助于提升模型的预测准确度.

图6 局部路网车道级邻接网络构建

与此同时，有学者开始认为基于先验知识及路网邻接关系所构建得到的拓扑网络可能难以充分体现出影响交通需求的内在属性，例如，用地性质、街区基础设施特征等.因此，基于可学习邻接矩阵的交通流预测研究同样也开始吸引学者们的关注，这种方法通过数据驱动的方式，利用深度学习模型从既有交通数据中学习得到一个邻接矩阵，再将其用于交通流预测.Diao等[45]提出了一种动态拉普拉斯估计器，从而将所得到的动态图结构输入图神经网络中进行预测，并证明了所提出的空间相关性学习过程(即动态拉普拉斯估计器)的有效性.此外，考虑到交通网络的动态变化特征，Li等[46]提出了一种结合图神经网络与循环神经网络的模型结构，使得深度学习模型能够在循环神经网络的每一个步长下生成一个邻接矩阵，从而反映出路网的时变特征.

2 现存挑战及未来研究方向

2.1 融合多维交通特征的预测模型

近些年来，尽管众多新颖的深度学习模型能够在城市道路短时交通流预测任务上取得更为准确的预测效果，但是这些模型往往只关注于从数据驱动的角度来探索城市路网的复杂时空相关性，而忽略了城市路网这一交通系统内在的固有特征.例如，城市路网内部的各路段之间，其道路等级、路段长度，以及道路基础设施等势必存在着一定的差异性，而这些因素均会对交通状态产生影响.对于未来的交通流预测研究而言，值得关注的交通特征包括：

1) 速度、流量等交通参数之间的关联性 现有的研究大多仅关注于单一交通流状态的短时预测，而忽略了多种参数之间的关联性.Zou等[47]基于copula联合分布函数的研究表明，微观交通流参数之间存在依赖性.未来的研究可以在预测模型中深入探索各参数之间的内在关联性，实现各交通参数未来状态的协同预测.

2) 路段之间的异质性 当网络级预测的节点为城市路网中的交叉口或断面时，拓扑网络中的边即代表连接各节点的路段.由于各路段长度、车道数等交通基础设施条件存在差异，则各相邻节点对于中心节点应具有不同的重要性.此外，如果将路网中的各路段视为网络中的节点，网络中的边则表征路段之间的相邻关系.而由于各路段具有不同的长度，不仅会导致各节点在整个拓扑网络中的重要性不同，同时也会导致长路段与短路段上所采集到的交通状态的准确性存在差异性.

3) 信号配时方案 城市道路交通流的一个最主要的特征就在于会在交叉口处受到信号设备的控制，从而给交通流带来间断流特征，并且造成其在短时间间隔下具有较强的波动性.在未来的城市道路交通流预测研究中，可进一步将信号配时方案与交通流时间序列数据有效融合，从而提升预测模型对于强波动性交通流数据的应对能力.

2.2 多源数据时空特征协同预测

现阶段，城市路网内部的交通状态检测设备可以划分为固定检测设备与移动式检测设备两种类型.其中，固定检测设备往往安装在城市道路交叉口处，而移动式检测设备主要为安装在出租车等浮动车上的GPS设备.从二者的安装位置及数据采集特点可以发现，固定检测设备能够准确统计断面交通信息，而移动监测设备能够反映出各路段上的交通状态.因此，可将二者采集得到的交通状态分别视为点数据以及线数据.前者能够反映进出路段的车流状态，而后者能够展现出路段内部的实际交通分布情况，而如果能够将点数据与线数据有效融合，则能够起到互为补充的作用，从而有助于进一步提升预测的准确性.

现阶段的研究往往仅单独考虑单一交通方式自身的出行需求预测，而忽略了各种交通方式之间的客流相似性与协同性.例如，城市公共交通系统大多面临着“最后一公里”难题，而共享单车的出现则为乘客乘坐公共交通出行提供了便利，即乘客能够搭乘共享单车前往就近的公交或地铁站点，从而实现各种交通方式之间的换乘，进而在多种交通方式的客流之间产生了协同性.因此，未来的研究可以考虑将多种交通方式的短时出行需求预测任务相结合，通过多任务、多图卷积等深度学习框架实现城市交通系统中各种交通方式的短时出行需求的协同预测.

但是，由于我国目前各种交通方式的运营数据均掌握在各自运营企业内部，而要达成以上目的，势必会面临数据壁垒的问题.出于数据安全与隐私保护的考虑，各种交通方式的运营数据之间难以实现数据共享.而要有效解决这一问题，未来的研究可以考虑引入联邦学习(federated learning)机制，从而在保障数据安全与用户隐私的前提下，使用机器学习或深度学习模型来进行短时出行需求预测.目前，联邦学习已被Liu等[48]应用高速公路短时交通流预测.但是，该项研究仅考虑了高速公路单一数据集的交通流预测，未来的研究可进一步将联邦学习机制拓展至城市交通系统中，从而深入挖掘各种交通方式客流之间的相似性与协同性.

2.3 基于归纳学习机制的多路网交通流预测方法

现实世界中往往会存在着在城市新区新建路网的情况.当新城区的道路网络投入运营时，由于缺乏历史数据进行模型训练，传统的预测模型难以在此种情形下得到应用.在这种背景下，很容易想到一种解决思路：将在其他路网中完成训练的模型引入此新建路网上进行交通流预测.虽然交通流预测领域已经历了四十余年的发展，大量新颖的预测模型的出现使得预测准确性不断提升，但是对于绝大多数预测方法而言，普遍在泛化能力上有所欠缺，难以满足以上需求.归纳学习是一种从个别现象推广至一般规律的深度学习模式，具有归纳学习能力的模型一般具有较强的泛化能力，能够有效应对未曾在训练集中出现过的实际数据.从交通流预测的角度来看，归纳学习则可以视为将在其他路网上进行训练的模型，在不经再次训练的情况下，直接应用于另一路网进行预测.同时，随着城市路网内部交通检测设备的不断完善，如果能够直接运用既有的图神经网络模型，来实现嵌入新检测器后的路网内部的交通流预测，则能够大幅节省深度学习模型所带来的开销.因此，这种模式除了能够解决上述提到的数据缺乏情况下的预测难题，同时还能够以一种普适性的模型来对多个路网的交通状态进行预测，从而大幅降低深度学习模型的训练开销与存储成本.

在图神经网络领域，具有归纳学习能力的传统图神经网络预测框架主要包括GAT以及GraphSAGE网络等.文献[43]在GAT模型的基础上，融合了GRU、双向LSTM以及残差连接结构，提出了一种名为STGGAT模型的预测框架，实验结果表明STGGAT模型与GAT模型均能在不加再次训练的情况下，直接应用于另一拓扑结构的路网上进行预测，并取得可接受的预测准确率.从现实世界中的交通管理需求来看，具有归纳学习能力的交通流预测模型具有较强的工程应用价值，因此未来的研究可以关注于在训练过程中引入子图切割的训练方式或者设计其他更为新颖的深度学习框架来提升模型在归纳学习任务上的预测效果.

2.4 融合时空复杂网络的路网流量预测

现阶段的路网级交通流预测研究普遍考虑将路网内的路段或检测器所组成的网络视为拓扑网络.除这种空间网络特性以外，已有利用复杂网络理论将交通流时间序列转化为复杂网络，进而对交通流的时变特征展开深入挖掘.Tang等[49]利用时间序列相空间重构方法搭建了交通流量复杂网络模型，并对复杂网络中的关键参数的设定进行了讨论分析.Yan等[50]利用复杂网络理论对交通流多元时间序列数据进行建模，并进一步从复杂网络角度对交通流特征展开分析.从网络构建的对象来看，现有的短时交通流预测中所使用到的拓扑图可以视为空间维度的复杂网络，能够反映出路网中不同位置的交通流状态之间的交互作用；而文献[49]的研究则代表时间维度的复杂网络，能够体现交通流的时间演化特征.从短时交通流预测领域的发展来看，充分探索交通流的空间关联性与非线性时间依赖性始终是研究热点，为了有效解决这一问题，包括LSTM、GRU以及注意力机制等在内的深度学习框架被广泛应用于此领域中.而这些方法往往注重于依靠深度学习的“黑箱”模式来挖掘交通流的时间序列特征，但是却缺乏可解释性.因此，未来的研究可以考虑将交通流时间序列的复杂网络特征与空间复杂网络相结合，引入多元时间序列复杂网络构建方法，来对于短时交通流的时空耦合特征进行建模，并与深度学习模型相结合进行预测，使预测方法更加贴合交通系统的真实演化规律.

2.5 基于时空kriging的交通状态估计及预测

在城市路网内部，出于检测设备安装成本与运营维护开销的考虑，交管部门难以在所有的交叉口处均安装检测设备.如果能够有效感知未覆盖检测设备的交叉口处的交通状态，则能够为城市路网的实时交通管理提供更为丰富的决策依据.同时，当交通状态估计的准确率达到一定可接受范围时，则能够有助于减少城市内部的交通检测器的数量，从而降低交管部门的运营成本.

而要解决以上问题，时空kriging任务便是一种可行的解决方案.交通流预测任务中的时空kriging任务可以概括为：利用路网中既有传感器获取到的交通流数据，来估计同一时段下未覆盖有传感器处的交通流信息.文献[51]提出了一种归纳图神经网络kriging模型，并设计了一种基于子图随机分割的训练策略.在多个高速公路数据集上的实验结果表明，所提出的预测框架能够有效提升模型的归纳学习能力，使其满足时空kriging任务的需求.与高速公路网络相比，城市路网具有更高的网络密度与连通性，如何充分利用城市路网内部的空间关联性以及考虑各路段之间的异质性，是未来城市路网时空kriging研究所不能忽视的问题.此外，未来的研究还可考虑将时空kriging与短时交通流预测任务相结合，既实现未覆盖检测设备处的交通流状态估计，同时还对其未来状态进行预测.

2.6 缓解城市道路交通流的强波动性

由于交叉口处的城市道路交通流会受到信号设备的管控，因此导致交通流受到周期性间断，这种间断现象会对交通流时间序列数据在短时间间隔下造成严重的振荡现象，从而给准确预测带来严峻的挑战.目前，已有学者将小波理论、EMD等数据降噪算法引入短时交通流预测中，并通过实验证明了该类方法的有效性.未来的研究可以考虑结合相位周期、交通事故、恶劣天气等因素，从数据降噪的角度对交通流的短时波动特征进行挖掘，消除高频噪声数据的影响，还原交通流数据真实变化规律，提升模型的预测准确性.

2.7 拓扑网络构建范式设计

近年来图神经网络逐渐成为了城市路网短时交通流预测领域中所使用到的一大重要工具.综合前文中的介绍，现阶段所应用的网络构建方法可以概括为：基于邻接关系的拓扑网络、基于距离阈值的拓扑网络、基于交通特征的拓扑网络以及基于可学习邻接矩阵的拓扑网络.这些方法均在可解释性、实际交通意义等方面具有各自特有的优势，导致现阶段在基于GNN的短时交通流预测种尚且缺乏一种通用的拓扑图构建范式.因此，深入探究哪种拓扑图构建方法更适合于城市路网短时交通流预测任务，也是未来研究中潜在的不可避免的一个问题.

3 结 束 语

本文针对于城市道路短时交通流预测这一热点问题，回顾了近年来的发展历程与主要研究方法.根据预测对象的空间范围，将现有研究按照单节点交通流预测与网络级交通流预测进行分类，分析了现有研究中存在的不足，并指出了融合多维交通特征、开展多源数据时空特征协同预测、提升模型归纳学习能力、有效融合时间维度复杂网络及空间维度复杂网络、开展时空kriging研究、缓解交通流时间序列数据的短时强波动性以及设计GNN拓扑网络构建范式等未来研究方向.