基于EMD-ARIMA组合模型的长江航运干散货运价指数预测

2022-11-10杨银花张矢宇

武汉理工大学学报（交通科学与工程版） 2022年5期

杨银花金雁汪敏* 张矢宇

(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (武汉理工大学交通与物流工程学院2) 武汉 430063)

0 引言

长江航运干散货运价指数(Yangtze River bulk freight index，YBFI)是用来反映我国内河干散货运输市场货运水平变动情况的重要航运经济指标.由于内河干散货市场的动态性和不稳定性都与沿海干散货市场有较大差异，例如，内河运价指数样本数据点少、周期性不明显且比沿海相关指数更容易受到外界因素的干扰等，沿海干散货相关预测分析方法不适用.现阶段对内河航运干散货运输市场波动分析及预测的研究较少，国内外学者主要对中国沿海散货运输市场的CBFI、国际(波罗的海)干散货运输市场的BDI和中国集装箱市场变化趋势的CCFI等进行了研究.主流的研究方法有：GARCH模型、小波分析理论、支持向量机(SVM)等.GARCH模型能够衡量波动的非均衡性，但精度无法保证；小波分析理论缺乏适应性，容易受到基函数选择的约束；SVM等机器学习方法容易出现过拟合导致预测失效[1-2].EMD是一种经验、直观、自适应的数据处理方法，能很好地提取非线性和非平稳性数据的时间尺度特征，结合传统预测方法从而克服单一方法的不足.

文中选取2009年5月—2021年4月YBFI月度数据为样本，结合“分解-预测-重构”分析思路，将EMD分解后的数据作为样本，从而降低数据噪声和网络复杂性，再对分解序列进行预测，综合得出最终预测值，从而提高YBFI预测分析的准确性.

1 模型原理

1.1 YBFI序列预测思路

YBFI时间序列具有含噪声、非线性、非平稳和多尺度性.现今对航运指数研究基本是单一算法预测或针对序列整体进行建模[3]，少有学者对数据的内在波动性出发进行预测研究.预测主要思想为“分解-预测-重构”[4].

采用EMD方法对YBFI序列进行降噪分解，得到不同频率周期相对稳定的YBFI本征模态分量(intrinsic model function，IMF)和趋势项(residual)；运用ARIMA模型或者Holt-Winters模型对子序列和趋势项进行预测，将各个IMF的预测结果进行集成组合即得到最终的YBFI预测结果.YBFI预测模型构建流程见图1.

图1 YBFI预测模型构建流程图

1.2 经验模态分解算法

经验模态分解算法(empirical mode decomposition，EMD)是一种处理非线性、平稳时间序列的前沿时频分析处理方法[5].分解得到不同波动时间尺度的IMF需同时满足2个条件：①各分量的极值点确定的包络线均值为0；②各分量通过极值点的个数与通过零点的个数不多于一个.具体建模步骤见图2.

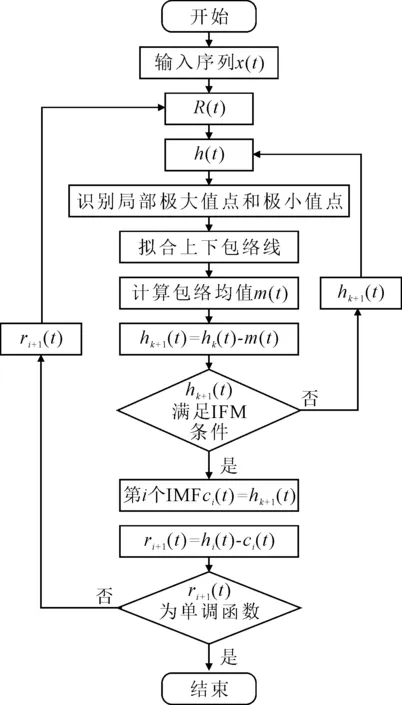
图2 EMD分解过程

1.3 ARIMA模型

ARIMA模型是将自回归过程(AR)与移动平均过程(MA)相结合的时间序列组合模型.其识别流程图见图3.

图3 ARIMA模型识别流程图

该模型的一般表示方式为：ARIMA(p，d，q)×(P，D，Q)S.其中：S为周期步长；d为非季节部分提取趋势信息所用的差分阶数；D为季节部分提取趋势信息所用的差分阶数.乘法模型的实质是通过差分将原始序列化为平稳序列，再对其进行拟合，其模型结构为

式中：{εt}为白噪声序列；Θ(B)为q阶移动平均系数多项式；Φ(B)为p阶自回归系数多项式；▽为差分算子；B为滞后算子.在ARIMA建模过程中，建模的重点在于确定(p，d，q)、(P，D，Q)的值.建模的主要思路[6]为：分析数据特征，对数据进行相应变换，直到通过ADF检验获得平稳时间序列为止，这是ARIMA建模的前提条件；根据ACF/PACF图形的峰值个数确定模型的参数，根据参数建模预测并对预测结果进行评估.

1.4 预测结果误差评估标准

根据统计学误差分析规则，选择下列7个指标作误差评价，见表1.

表1 误差评估指标

2 实证过程

2.1 数据来源及样本

由于2008年1月—2009年4月数据振幅较大，初步预测结果与现实情况不符.为了准确预测长江航运干散货2021—2030年的运价指数数据，选取交通运输部长江航务管理局官网公布的从2009年5月—2021年4月共144个样本数据.对数据进行初步调整并绘制时序图，见图4.

图4 长江航运干散货运价指数(YBFI)时序图

2.2 YBFI序列的非线性、非平稳性检验

由图4可知：数据呈现出较明显的季节性和波动性，具有明显的非线性特征.在Eviews软件中进行ADF非平稳性检验，见表2.t统计量(-2.893 456)大于不同显著水平下的临界值，在10%置信水平下不拒绝存在单位根的假设，P值(0.167 8)大于0.05，故YBFI序列是非平稳序列.

表2 ADF非平稳性检验结果

2.3 EMD分解

EMD方法相比传统的小波分析、傅里叶分解方法存在一定的优势，EMD脱离了预定好的基函数的约束，能够最大程度保留时间序列自身的特性.YBFI序列经EMD分解后得到三个IMF分量和一个趋势项Residual，见图5.

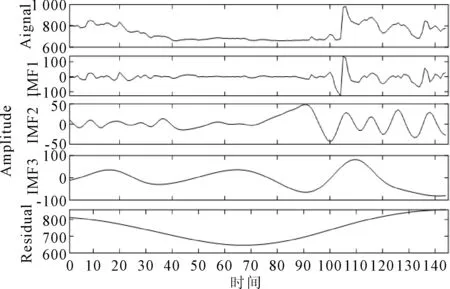
图5 EMD分解结果

由图5可知：IMF1的波动频率最高，并依次递减，平均振幅也从大到小变动，表现出YBFI序列的内在多尺度波动特性.从周期性角度看，IMF1的周期最小，初步分析是市场基础经济要素对YBFI序列的影响；IMF2、IMF3依次变大，初步分析IMF2是政府宏观调控，定期出台的政策规定对YBFI的影响，而IMF3则可能是航运市场重大事件影响，例如2008年金融危机、2020年新冠疫情等.趋势项自2008年(根据官网数据可得)便呈现缓慢下降趋势，到2014年末2015年初达到谷值，之后开始缓慢增长，查阅有关资料，航运市场中周期为10～15年[7]，这与趋势项展示的规律一致.

2.4 预测和重构

通过EMD分解将YBFI序列分解为相对平稳的IMF分量，将三个IMF分量运用ARIMA模型或Holt-Winters指数平滑法进行比较、预测、分析，此类分析主要在SPSS和Eviews软件中实现.趋势项Residual数列采用曲线拟合方法，根据其分布特征和干散货运输市场的周期波动特性，运用MATLAB 2018a实验平台进行拟合研究，通过训练，发现三角函数对Residual数列的拟合效果较好.

1) IMF1拟合模型通过拟合发现ARIMA(2,0,10)×(2,0,0)12能够很好的反映IMF1序列的波动特性.其拟合优度R2为0.483(接近0.5，拟合较好)，均方根误差RMSE仅为21.093；DW统计量为2.032；AIC值为9.034.

2) IMF2拟合模型通过比较ARIMA模型、指数平滑模型以及专家建模结果，发现ARMA(4,7)能对IMF2的周期、波动特性进行很好的预测.其R2达到了一般线性拟合模型R2，为0.996，接近1；均方根误差RMSE仅为1.257；平均绝对误差MAE仅为0.803；DW值为1.672；AIC值为3.102.

3) IMF3拟合模型通过比较拟合发现ARMA(6,1)能对IMF3的特征数列进行较好的拟合.在该模型拟合过程中，R2为0.998，几乎等于1；均方根误差RMSE与平均绝对误差MAE均处于较低区间，DW值为1.912，说明拟合精度较优.

4) Residual拟合模型趋势项主要反映了YBFI序列在发展过程中的整体趋势和变化周期.经过在MATLAB实验平台中反复验算，调参，最终确定该序列的较优拟合、预测模型方程式为

Residual-PREt=778.2+14.49×

cos(t×0.027 86)-95.89×sin(t×0.027 86)+

24.64×cos(2×t×0.027 86)+

22.71×sin(2×t×0.027 86)-3.695×

cos(3×t×0.027 86)+0.497 1×

sin(3×t×0.027 86)

式中：Residual_PREt为第t期趋势项Residual的预测值；t为时间序号，记2009年5月为t=1；依次往后t=2，3，…，n.

图6为Residual的拟合预测模型效果和残差分析图.

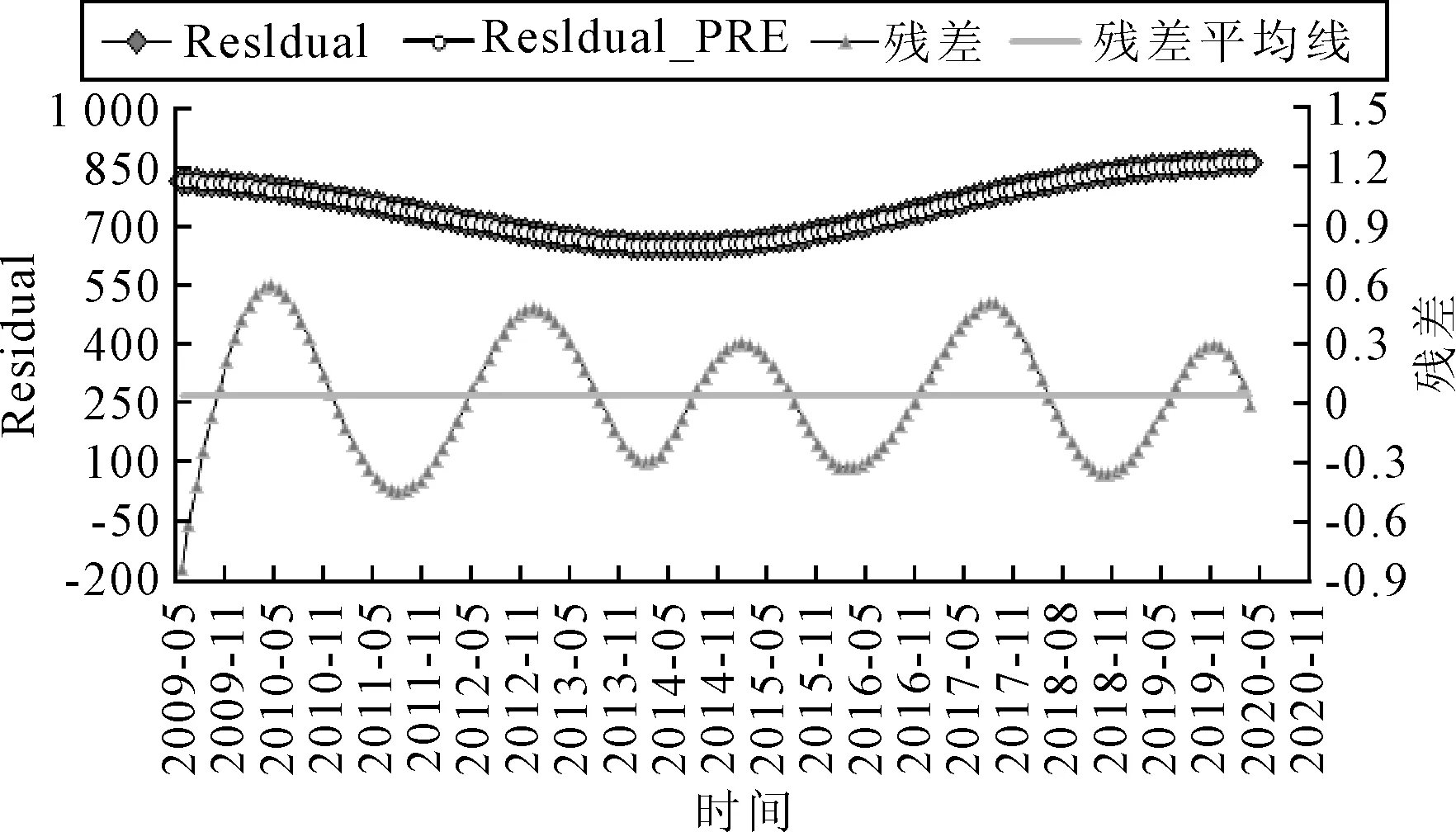
图6 Residual拟合与残差分布

从残差分布曲线，发现拟合效果较好，残差基本在[-0.95，0.60]之间，且平均残差仅为0.036 09，与0无明显差异.

5) YBFI预测结果由式(1)，将上述经验模态分量和趋势项求和即可得到相应年份YBFI预测结果，见图7.

图7 YBFI拟合效果图

预测值略有滞后，但基本能够反映样本波动规律和变化趋势.通过计算，得到残差均值仅为0.312 8(与0无明显差异)，说明总体误差水平较低；均方根误差RMSE为20.317，若以基期1 000点算，均方根误差仅为2%，说明高值部分预测效果较好；平均相对误差绝对值MAPE为1.62%，在10%范围内，表明平稳部分预测效果较好；平均绝对误差MAE=12.184；相对误差RE中仅有五组数据超过5%，2组数据超过10%，占样本总数的比例分别为0.034 7、0.013 9，可忽略不计，故可判断整体误差较低；R2为0.973 5，说明该模型对YBFI序列的预测效果较准确.