基于EEG的船舶驾驶员工作负荷识别研究

2022-11-10万志远陈俊华

武汉理工大学学报（交通科学与工程版） 2022年5期

刘清万志远杨柳* 何萌陈俊华杨锬

(武汉理工大学交通与物流工程学院1) 武汉 430063) (国家水运安全工程技术研究中心2) 武汉 430063)

0 引言

人为因素占水上交通事故的75%～96%[1-4]，且任何海事事故中都包含人为因素[5].研究表明脑电信号与包括航空[6]、公路[7]在内的驾驶行为存在相关性，有研究者将人为因素分为工作负荷、情绪、注意力、压力和疲劳五类[8].其中工作负荷(mental workload)与铁路机车驾驶员的疲劳程度存在正相关关系，与汽车驾驶员在驾驶中的视觉行为也存在强相关性[9].在心理层面，工作负荷会对飞行员的决策产生影响.工作负荷的研究方法可以分为主观研究和客观研究.主观研究方法包括主观打分评价法、心理量表问卷等；客观研究方法包括绩效评价、生理信号研究等.其中生理信号研究包括了脑电波(electroencephalogram, EEG)、眼动、心率变化、皮电、肌电、血压、体温等多种指标.

近年来，脑电分析方法也从早期的时域分析发展到了频域分析、时频域分析、空间域分析方法.频域分析方法多应用于交通安全中的人为因素研究，使用脑电信号研究交通参与者的工作负荷、情绪、注意力、压力和疲劳等.工作负荷可以视作中枢神经系统处理外界任务的脑力负荷，影响与中枢神经相关的功能结构以及其他生理过程，而这些生理过程可以较为方便地去感知与研究.同时，脑电各个频段对于工作负荷的变化敏感，采用模式识别可以正确识别各频段的工作负荷水平，并有较高的识别准确率.

支持向量机(support vector machines, SVM)是模式识别研究中一种常用的模型，它是定义在特征空间上的间隔最大的线性分类器.通过SVM的核函数，在特征空间中投影数据，以此来获取最优超平面，从而建立分类器.这种算法在解决小样本、非线性及高维模式识别问题中具有一定的优势，有良好的通用性和鲁棒性.

尽管基于脑电的工作负荷研究具有生理活动较易检测、针对频段模式识别准确率较高的优点，但目前脑电研究还存在一些局限性，如脑电采集设备体积庞大、被试人员不能移动、脑电信号中干扰信号难以去除等问题.同时，水上交通具有需要多人协同驾驶、驾驶员频繁移动等特点，制约了大型脑电设备在水上交通领域研究的应用.文中使用移动式无线脑电采集设备，在船舶驾驶员的工作环境中正常采集脑电信号，借助脑电数据识别船舶驾驶人员的工作负荷.

1 船舶驾驶员脑电数据采集实验与实施

1.1 实验方案设计

船舶模拟系统基于全任务大型船舶操纵模拟器构建，使用Navi-Trainer Professional 5000型设备.模拟系统具备与真实船舶相同或高度近似的综合船桥驾驶台、船舶控制系统、雷达系统、导航系统、通信系统等.脑电采集仪为Neurosky公司的Mindwave Mobile 2，采集频率512 Hz，FP1单通道，使用耳垂电极作为参考.

被试人员46名，均为男性.其中有8人正在接受船长岗位培训，38人正在接受大副岗位培训.被试人员的年龄为(36.5±6)岁，有(11.4±6.4)年驾龄，具有长期的驾驶经验，在实验过程中能够表现出更为职业化的反应.

1.2 实验实施

被试人员随机分为若干个四人小组，每个小组内四人轮流扮演船长、驾驶员、通信员和舵工四类船员角色.

实验场景由固定事件和随机突发事件组成，实验时长平均45 min.场景流程为：离泊、正常航行、能见度降低及恢复、随机突发事件(包括火灾、溢油、船舶碰撞、人员落水、故障、搁浅、风浪、船舶追越、会遇)，根据突发事件处理结果进行靠泊或终止实验.

完成实验后，实验人员获取了被试人员的全程脑电数据、场景录像和每场实验的事件时间轴作为实验数据.其中脑电数据记录了52人·次，每人·次的数据记录时长为45～60 min不等，每秒记录512条脑电信号，以45 min计算约为130万条未经筛选的脑电信号原始数据，原始数据为脑电采集设备的配套软件直接记录的电位差，保存为单通道时间序列结构.

综合考虑船员在正常航行和突发事件处理场景下不同的船舶驾驶任务、通信时长、舱内沟通频率频次等，将正常航行场景标定为低工作负荷状态，将突发事件处理场景标定为高工作负荷.

2 船舶驾驶员脑电数据特征分析

2.1 脑电数据预处理

1) 由于设备采用干式单电极，稳定性和精度容易受到影响，而且脑电波的信号强度极低，通常以μV为单位波动，需要人工检查脑电信号数据，通过对波形的观察，初步筛选，剔除噪声信号过大的无效数据.

2) 考虑到采集的脑电信号中存在身体活动(移动、眨眼、讲话等)和设备本身电信号的干扰，使用带通滤波和陷波滤波的方式排除部分干扰信号.具体到脑电信号的频段，本文的研究对象为0.5～80 Hz频段的脑电信号，为了保证数据的完整性，有限长单位冲激响应滤波器(finite impulse response, FIR)低通滤波的截止频率为0.5 Hz,高通滤波的截止频率为100 Hz.考虑到脑电采集系统的设备供电，将陷波滤波器的中心频率设置为50 Hz.

图1为预处理前后数据对比.由图1可知：预处理操作经过滤波后，剔除了部分噪声信号(即图中的部分波峰信号)，平滑了原始信号，保留了有效数据.整体波动趋势和原始信号保持一致.

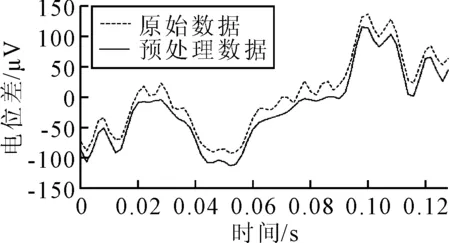
图1 预处理前后数据对比

2.2 脑电特征量提取

脑电信号可以根据频段分为δ波、θ波、α波和β波，不同频段的脑电波是大脑功能区域在生理活动中产生的，例如频率为8～13 Hz的α波通常在安静或清醒状态下最为显著，频率为14～30 Hz的β波通常在紧张或专注状态下较为显著.具体频率划分和对应的功能活动见表1.

表1 脑电波频率及功能划分单位：Hz

功率谱密度(power spectral density, PSD)是脑电信号在单位频带内的功率，表征了脑电信号在不同频率上的功率强度分布.使用周期图法计算PSD，其计算公式为

(1)

脑电信号是一个有限长度的时间序列，因此将式(1)改写为

(2)

在Matlab中使用式(2)，计算出的功率谱密度见图2.其中50 Hz频率上功率的减少是由于陷波滤波器的中心频率设置为了50 Hz，同样地，由于带通滤波器的高通截止频率为100 Hz，功率谱密度的图像并未显示100 Hz以上频率的功率谱密度.在此基础上，分别对0.5～3，4～7，8～13和14～30Hz频段进行积分运算，提取了δ波、θ波、α波、β波的功率，将四种脑电波的功率记做Pα、Pβ、Pθ、Pδ.

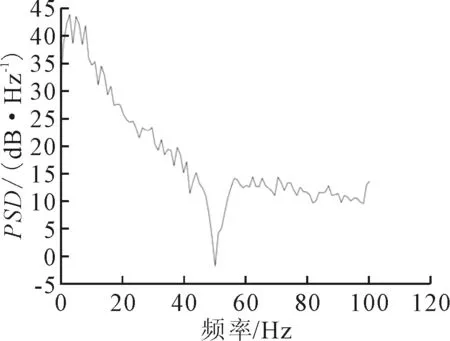
图2 数据经过处理后获得的功率谱密度图

2.3 不同工作负荷下船员脑电数据特征方差分析

由于α波和β波分别对应大脑放松和注意力集中的状态，因此考虑分析Pα和Pβ的比值与工作负荷的相关性.在不同工作负荷水平下进行多次采样，获取样本，根据工作负荷水平分为两组(低工作负荷水平、高工作负荷水平)后进行方差分析.其中P1为正常航行场景，即低工作负荷水平下的数据组，P2为突发事件处理场景，即高工作负荷水平下的数据组.

具体计算中将脑电数据以10 s长度分段，分别计算各数据段脑电特征值.低工作负荷水平下各个分段数据计算得出的α波特征值依次记做

式中：y为在低工作负荷水平下的数据分段数量.

高工作负荷水平下各个分段数据计算得出的α波特征值依次记做

式中：z为在高工作负荷水平下的数据分段数量.

计算后得出，两组数据的在方差齐性检验上的显著性均远大于0.05，证明两组数据具有方差一致性，可以进行单因素方差分析，结果见表2.

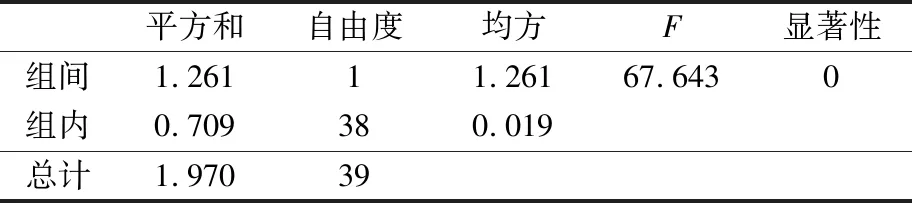
表2 单因素方差分析

由表2可知：单因素方差分析的显著性水平远低于0.05，证明P1和P2两组数据存在显著性差异.因此，Pα/Pβ指标在不同工作负荷水平下的水平存在差异，即Pα/Pβ指标可以满足识别模型对输入参数的要求，以识别低工作负荷水平和高工作负荷水平.

3 基于EEG的船舶驾驶员工作负荷识别模型

3.1 模型构建与训练

核函数及其参数是SVM的一个重要部分，影响SVM的学习能力和泛化能力.径向基函数 (radial basis function, RBF)具有映射维度广、决策边界多样和表现稳定等优点，被广泛应用于基于SVM的分类研究[10].因此，选用RBF核函数开展工作负荷模型研究.

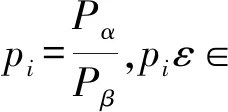
选取适当的核函数K(x,z)罚参数C>0，构造并求解凸二次规划问题.

(3)

(4)

0≤αi≤C,i=1,2,…,N

(5)

在选择RBF作为核函数的情况下，分类决策函数为

(6)

选择网格搜索进行交叉验证，作为惩罚系数C和核函数参数gamma的优化算法，网格搜索法优点是可以得到全局最优解，交叉验证可以提高训练集分类的准确率.

从实验数据中选择了50组低工作负荷状态的脑电信号数据和50组高工作负荷状态的脑电数据，共计100组数据，每组数据均为长度为10 s的原始数据，使用Pα/Pβ作为特征指标，输入本章所述的SVM模型，使用四折交叉验证方法进行训练.完成网格搜索算法后，获得最优惩罚系数C=1.319 5，最优核函数参数gamma=9.181 6.C和gamma是SVM模型的关键参数，可以代表SVM模型的训练结果.

使用随机选取的25组训练集数据输入训练后的SVM模型，得到了每组数据的工作负荷水平识别结果，见图3.该模型正确识别了其中24组数据的工作负荷水平，训练集识别准确率达到了96%.因此在最优惩罚系数C=1.319 5，最优核函数参数gamma=9.181 6时，SVM模型的参数达到了最优.

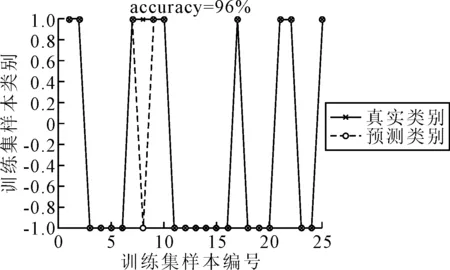
图3 SVM训练集预测准确率

3.2 模型评价

从训练集之外的数据集中，随机选取了25组不同工作负荷水平的数据作为测试集，输入训练好的SVM模型后得到了25组数据的工作负荷水平识别结果，见图4.与测试集的真实工作负荷对比，模型识别出的结果仅有2组数据错误，测试集的识别准确率达到了92%.

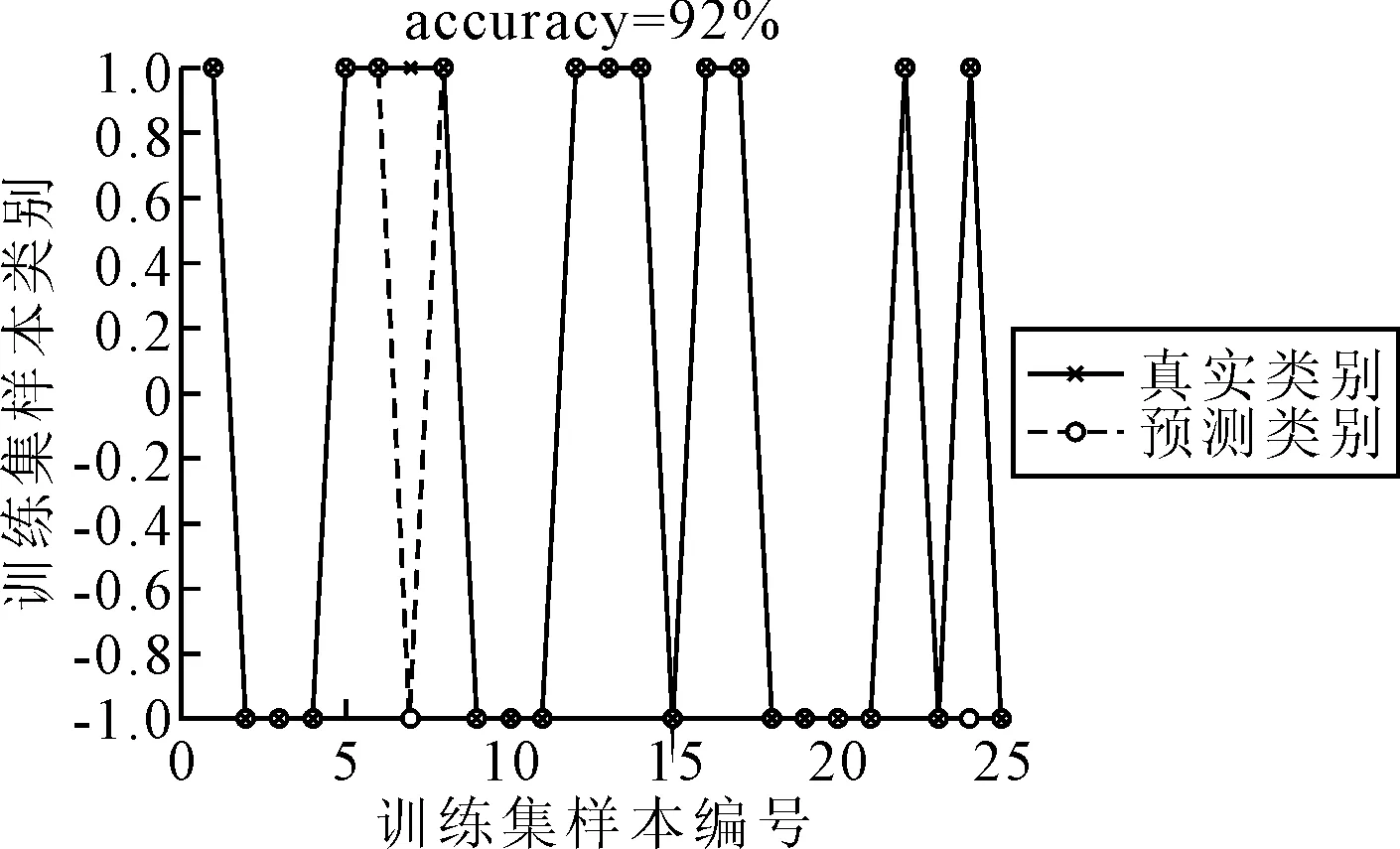
图4 SVM测试集预测准确率

Macro-ROC曲线是以SVM模型分类结果的真阳性率(true positive rate, TPR)为Y轴，以假阳性率(false positive rate, FPR)为X轴绘制的曲线图，能够对多种分类器的性能进行评价.在曲线图中，曲线越趋向图像左上角(0,1)点，表示SVM模型的分类性能越优秀.相反的，曲线越趋向于图像的右下角(1,0)点则表征SVM模型分类器的分类性能越差.通过Macro-ROC曲线图，可以直观地定性评价SVM模型的分类性能.

Macro-AUC值与Macro-ROC曲线相关，通过计算曲线下的面积求得，用于评价多种分类器的性能，在本文中用于评价SVM模型的分类性能.一般条件下，Macro-AUC取值为[0,1]，AUC的值越趋近于1，表示模型的分类性能越好，相反的，越趋近于0，则表示模型的分类性能越差.Macro-AUC的值可以定量地评价SVM模型的分类性能，评价结果见图5.

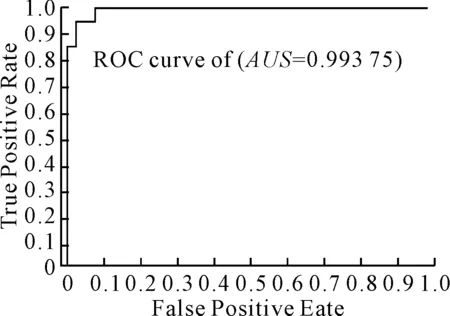
图5 Macro-ROC曲线图

由图5可知：Macro-ROC曲线趋向于左上角(0,1)点，表示训练好的SVM模型分类性能较为优秀，同时Macro-ROC曲线下的面积，即Macro-AUC值为0.993 75，接近1，表示训练好的SVM模型分类性能较为优秀.上述评价指标的评价结果基本相同.

综合上述指标，训练完成后的工作负荷识别模型使用随机选取的包含不同工作负荷水平的新数据作为测试集，可以达到92%的识别准确率，且Macro-AUC值可以达到0.993 75，Macro-ROC曲线贴近左上角.因此基于EEG的船员工作负荷识别模型能够较好地识别船员在不同实验场景下的实时工作负荷水平，取得了较好的分类效果.同时，也证实了船员不同的工作负荷会对船员的脑电活动产生一定影响.