基于M-LSTM的股票指数日内交易量分布预测研究

贺毅岳, 刘 磊, 高 妮

(1.西北大学 经济管理学院,陕西 西安 710127; 2.西安外国语大学 经济金融学院,陕西 西安 710128)

0 引言

随着计算机和通讯技术的飞速发展，算法交易已成为一种基金、券商和投行等机构投资者采用的主流量化交易方式。算法交易一般分为被动型和综合型两类，其中被动型的交易量加权平均价格(VWAP)策略基于日内交易量的预期分布，将大额委托单按照区间交易量占总成交量的比例拆单交易，以期实现最终买入或卖出的成交价接近于市场均价，从而减小大额交易面临的市场冲击成本[1]。VWAP策略的核心是对日内区间成交量分布的预测，预测结果的准确度很大程度上决定了VWAP策略的执行效果[2]。

目前对VWAP策略的研究聚焦于日内区间交易量分布的预测建模问题。Berkowitz[3]首次提出了传统的VWAP交易策略，利用交易价格与VWAP的差额来衡量其对市场的冲击成本。YE等[4]用换手率作为成交量的代理变量，将其分为常规部分和特殊部分，利用主成分分析法结合ARFIMA和ARMA模型，对股票换手率的特殊部分进行建模。夏晖等[2]将日内成交量分解为市场共同部分和个股特殊部分，并对这两部分分别进行建模预测，其改进策略比传统VWAP策略适应性更广、跟踪误差更小。张帅[5]运用随机森林和前馈神经网络方法构建日内成交量比例预测模型，获得了比传统滚动平均方法更高的预测精度。

上述研究在日内交易量分布预测问题上取得了较好的实证效果，但存在一定的理论或实用性缺陷。首先，股市信息的不对称特征使得日内成交量时序反映市场走势的同时包含大量随机噪声，导致现有预测建模方法适用于市场的时效性较弱；其次，日内交易量分布通常具有U型结构特征，这种时变的结构性波动是成交量分布预测的难点[2]，导致现有预测模型对历史样本依赖性较强、泛化能力较弱；最后，浅层机器学习算法应用于高维数据时存在维数灾难与特征表示低效等缺陷[6]，难以实现对日内交易量分布的高效预测。

随着对金融预测研究的不断深入，学者们发现结合深度学习与经验模态分解方法可有效提升金融时序的预测精度。Thomas等[7]发现利用LSTM神经网络预测非线性金融时序的精度显著优于随机森林、Logistic回归等模型。乔若羽[8]通过建立基于注意力机制的LSTM、RNN等神经网络模型对股票进行预测，实证检验了结合注意力机制的神经网络模型在金融时序预测中的优异表现。贺毅岳等[9]将CEEMDAN方法引入到股市指数预测建模中，构建CEEMDAN-LSTM模型，实证表明该模型相较于SVR、MLP和LSTM模型预测误差更小，验证了经验模态分解方法可提升股票指数预测的有效性。李成等[10]提出基于MEMD方法的股市收益与宏观经济活动关系的分析方法，验证了MEMD在多维经济金融时间序列处理方面的优势。

综上所述：相较于传统的计量、统计及浅层机器学习模型，深度学习在非线性、非平稳数据处理以及数据复杂特征提取等方面具有较大优势[11]。股票日内成交量序列呈现非线性、非平稳和高噪声特性，导致现有模型难以充分提取股票日内成交量的波动特征。为更有效地刻画指数日内交易量分布的复杂变化模式、剔除市场噪声，需对指数日内交易量时序进行分解和重组。为此，本文引入MEMD对日内交易量多元序列进行分解、重组，在数据去噪的同时有效保留交易量时序数据的结构波动特征；进而充分考虑基于注意力机制的LSTM网络能高效提取复杂多元序列中长期依赖关系的优势，运用LSTM-Attention对重构的日内交易量序列进行预测建模，提出MEMD分解下基于LSTM-Attention的股票指数日内交易量分布预测模型M-LSTM。

1 预测建模的理论基础

1.1 多元经验模态分解MEMD

MEMD对传统的经验模态分解(EMD)进行改进，将EMD的处理信号从一维拓展到多维，实现了多通道信号的联合处理，有效克服了EMD、小波分解等方法在多维信号处理方面的局限性[12]，并具有自适应性和时频局部化能力。MEMD算法原理如下[13]：

(2)计算v(t)=[v1(t),v2(t),…,vn(t)]T这个n维信号向量组在方向向量集xθk每个方向上的映射pθk(t)，k∈[1,K]。

(6)计算模态函数h(t)=v(t)-m(t)，判定h(t)是否满足多元IMF的判断标准。如果判定符合，则定义h(t)为第一阶IMF分量，并将m(t)作为新的输入信号，重复进行(2)～(6)的迭代过程；反之，若不满足，则将h(t)作为新输入信号，重复进行(2)～(6)的迭代过程，直至满足最终条件。

通过上述步骤，将原始信号v(t)=[v1(t),v2(t),…,vn(t)]T分解为一系列的IMF分量和一个残差项r(t)，且各维度分解所得到的IMF数量相等、频率分布相同。

1.2 LSTM模型概述

循环神经网络(RNN)是一种处理序列数据的神经网络。RNN理论上能很好地处理序列数据，但经典RNN在参数优化时会出现梯度消失和梯度爆炸问题。Hochreiter等[14]提出了图1所示的长短期记忆神经网络(LSTM)模型，有效解决了RNN长期依赖与时滞性问题。LSTM通过引入由输入门、遗忘门和输出门构成的门控单元系统，改进了传统RNN的隐层结构。其中，遗忘门用于控制LSTM模型中哪些信息需要从神经元状态中移除，包含两个输入ht-1和xt,通过sigmoid函数映射后输出值在0～1之间。输入门用来更新单元状态，由两部分构成：it控制什么信息被输入，决定LSTM需要更新什么值；Ct表示创建一个新的候选值向量，用这两个信息对单元状态进行更新。输出门控制输出到下一时刻神经元的信息。LSTM各层计算公式如下：

ft=σ(wf[ht-1,xt]+bf)

(1)

it=σ(wi*(xt,ht-1)+bi)

(2)

Ct=tanh(Wc*(xt,ht-1)+bc)

(3)

Ut=it*Ct+ft*Ct-1

(4)

Ot=σ(Wo*(xt,ht-1)+bo

(5)

ht=Ot*tanh(Ut)

(6)

其中ft、it、Ot分别表示遗忘门、输入门和输出门；Wf、Wi、Wo和bf、bi、bo分别表示每种门的权重矩阵和偏置量；Ut、ht和σ分别表示单元状态、隐藏层输出、Sigmoid函数。

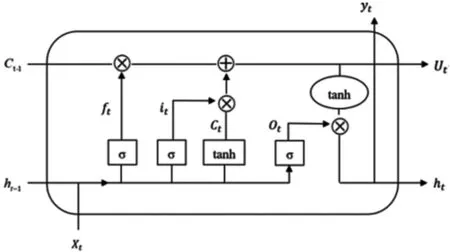
图1 LSTM单元内部结构

1.3 基于注意力机制的LSTM模型结构

注意机制是一种自动加权方法，能有效获取输入神经网络中各维度时序的贡献度。为高效获取交易量时序数据中的重要信息，本文提出一种注意力机制的LSTM模型结构。其中，为防止在LSTM层之后加入注意力机制导致一部分注意力被其他特征分散的问题，本文在LSTM层之前加入Attention机制。

图2 基于注意力机制的LSTM模型结构

图2为本文基于注意力机制的LSTM模型结构，建模采用的数据结构形式为：将第t天的交易时间划分为M个区间，xtm表示第t天的第m个区间交易量占全天总交易量的比例，m=1,2,…,M，第t天的交易量占比表示为向量(xt1,xt2,…,xtm,…,xtM)，则k个连续交易日的交易量占比序列可表示为输入矩阵：

相应地，在图2所示的模型结构中，将多维时间序列X传入全连接层，通过注意力机制计算不同时刻从全连接层中输出特征向量的权重系数α1、α2、…、αM，生成权重矩阵α。然后，将输入矩阵X与权重矩阵α的乘积累加求和，得到最终输出的特征矩阵v。权重矩阵α和特征矩阵v的计算公式为:

ui=tanh(Wsxij+bs)

(7)

(8)

(9)

其中Ws、bs、us分别表示偏置量、权值矩阵、随机初始的时间序列注意力机制矩阵。然后，将筛选后的多维时序作为LSTM单元节点的输入，得到对应LSTM层输出h1、h2,…,hM。最终，时序数据经特征提取和神经网络层映射处理后，获得与原始输入时序测试集对应的模型预测输出向量(y1,y2,…,yM)。

2 预测模型M-LSTM的构建

2.1 M-LSTM建模思路及流程

如图3所示，M-LSTM模型以5分钟日内区间交易量占比多元时序数据为输入，利用MEMD对多元时序进行分解与重构，剔除高频噪声，提取各维度子序列的波动特征，再运用LSTM-Attention对各维度重构后的序列进行预测建模，以获得高精度的指数日内交易量分布预测效果，主要处理过程包括：

图3 M-LSTM模型的主要处理过程

步骤1将原始指数5分钟区间交易量时序进行数据转化为5分钟区间交易量占全天总交易量比例的交易量占比多元时序数据。

步骤2运用MEMD将交易量占比多元序列分别分解为n个本征模函数IMFi(i=1,2,…,n)和一个残差项Rn(t)。

步骤3逐次剔除部分高频IMF、重构交易量占比多元序列，建立相应的日内交易量分布LSTM-Attention预测模型，并从预测有效性角度对高频IMF的组合方式进行优化。

步骤4利用已建立的LSTM-Attention预测模型，对降噪重构后的指数交易量占比多元时序进行滚动预测。

2.2 区间交易量多元序列的MEMD分解

选取2013/1/1至2020/5/1期间上证综指日内5分钟区间交易量时序数据，剔除节假日、缺失值后剩余1779个有效交易日数据，每日包含48个日内交易量区间，共85392个区间交易量数据，作为预测建模的初始数据。计算交易日内48个区间交易量占日内总交易量的比例，形成新的日内区间交易量占比多元时序数据，其逻辑结构为(1779×48)的矩阵。运用MEMD对交易量占比多元时序数据进行分解，结果数据形式为(11×48×1779)。48维日内区间交易量多元序列中的每一序列均被分解为10个模态分量IMF和1个残差项。图4为其中第1维序列分解结果，即1779个交易日内首个5分钟区间交易量序列的分解结果，展示了第1维区间交易量序列在不同时间尺度下的波动模式，图中横轴表示时间序号，纵轴表示IMF的振幅。

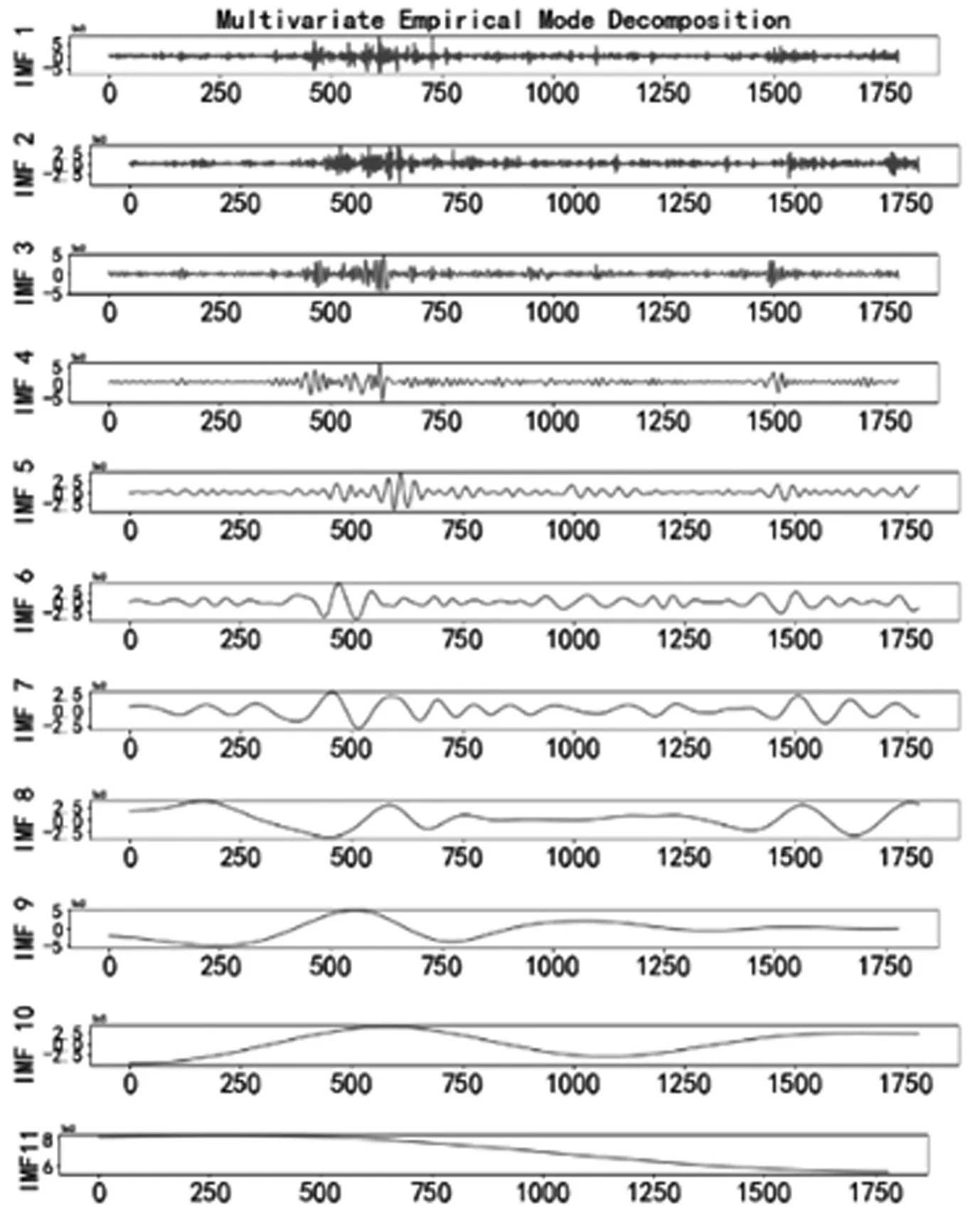
图4 区间交易量序列的MEMD分解结果

2.3 基于LSTM-Attention的交易量预测建模

利用python开源库Keras构建LSTM-Attention神经网络预测模型。采用滚动预测建模的方式，以最近30个交易日的日内区间交易量占比为输入来预测下一交易日的区间交易量占比[15]。初始预测建模时选取2013/1/4至2018/4/12共1279个交易日的日内区间交易量占比多元序列数据构建模型训练集，利用pandas将其表示为(1279×30×48)的DataFrame数据对象。然后，以剩余的500个交易日日内区间交易量占比数据构建维度为(500×30×48)的测试集。模型的输入、输出均为48维的日内区间交易量占比数据。

LSTM-Attention网络的计算结构依次包含输入层、全连接层、注意力机制层、3个LSTM层以及全连接层和输出层。考虑到金融时序非线性和复杂性特征以及模型的运算效率，所建立的LSTM-Attention神经网络模型共设有4个超参数，包括隐藏层个数、学习率、各层神经元数量和输出层维度。选取优化器Adam进行参数优化，使模型的损失函数快速收敛至全局最小值。模型经过多次训练稳定后，获得的最佳参数为：激活函数为linear，动态学习率为0.005；注意力机制内部激活函数为softmax，且含有4个隐藏层。通过实验确定各隐藏层神经元数量，不同神经元个数设置下模型的预测表现如表1所示。综合考虑模型的预测精度和运算效率，将每个LSTM层中神经元的个数设置为26。模型训练过程中每次投入模型的样例数据大小batch_size设置为32，迭代次数设置为100。

表1 不同神经元个数下预测模型的评估结果

2.4 基于IMF重组优化的交易量数据重构

MEMD分解根据含噪信号的固有时频特性，将多元时序数据按频率高低分解为多个IMF，且随着分解层数的增加所得到的IMF频率逐渐降低，信号对IMF的主导性增强而噪声对IMF的影响逐渐减弱[13]。金融市场数据中噪声通常集中在高频段，而信号集中在低频段，故MEMD分解得到的高频IMF通常为噪声[16]。本文通过优化IMF重组方式重构日内交易量占比数据，具体过程如下。

首先，对48维交易量占比时序数据中每一维度的IMF分量分别进行均值为0的t检验。结果显示各维度的IMF1～IMF7均值显著非0，故将IMF1～IMF7作为原数据的高频部分，IMF8～IMF10为低频部分，IMF11为残差项。其次，鉴于高频部分波动剧烈且含有较多噪声，故本文试图通过优化各维度区间交易量占比时序中高频IMF序列的组合方式，以实现去噪的同时保留其中包含的交易量短期波动趋势信息。从图4可知，高频IMF1～IMF7中IMF3～IMF7频率相对更低，包含区间交易量分布的波动信息相对更多，而IMF1、IMF2则含有更多的噪声，故重构的区间交易量占比序列至少应包含IMF3～IMF11。最后，针对不同IMF组合方式构建LSTM-Attention预测模型，进而根据表2所示的预测评估结果确定最优的IMF组合方式，即剔除IMF1后由IMF2～IMF11重构获得的区间交易量占比多元序列预测效果最好。

表2 不同IMF组合方式下预测模型的评估结果

3 对比实验及结果分析

3.1 实验设计及各方法的预测效果对比

以测试集500个交易日内48个区间中各区间内交易量占比的预测值与真实值之间的平均绝对误差，来测度各模型的预测有效性，同时可增强各模型预测结果对比的可视效果。误差计算方式见式(10)。

(10)

其中i为交易日序号，i=1,2,…,N，j为日内区间的序号，j=1,2,…,48；MAEj表示第j区间的平均绝对误差；Yij表示第i日内第j区间交易量占比的预测值；Zij表示第i日内第j区间交易量占比真实值；N为总交易天数，N=500。

以上证指数日内交易量占比的原始时序数据作为输入，分别应用已有研究中预测性能较好的指数预测方法作为M-LSTM的对比方法，包括：SVR、ARIMA、LSTM和动态区间交易量分布预测方法，构建相应的交易量分布预测模型，并进行滚动预测。图5所示为M-LSTM、LSTM、动态因素分解、MEMD-LSTM、SVR以及ARIMA模型在各区间内的平均绝对误差对比效果。相较于LSTM、动态因素分解、SVR和ARIMA模型，M-LSTM在各区间内预测误差更小，且在大多数区间内平均绝对误差保持在0.2%～0.3%，预测表现更好。M-LSTM与MEMD-LSTM、动态因素分解方法对应的平均绝对误差曲线较为接近，各区间内误差相差较小，但在多数区间M-LSTM的预测误差仍然最小。

图5 各模型预测效果对比

另可看出，在市场刚开盘半小时区间、下午开市的前后五分钟区间和收盘前十分钟区间内，各模型的预测误差都比较大，而其他区间内误差较小且平稳，这是由我国股市T+1交易机制所导致的。大部分交易者受学习和工作时间限制，只能在各交易日内开盘、收盘及午间休市阶段，依据股指成交量的多少等市场信息来判断市场走势、决定是否交易，而模型很难捕捉并学习到这种因投资者心理、行为特征引起的即时、大幅度的交易量突变，从而导致相应时间段内模型预测误差较大。

表3进一步给出了上述各模型的多指标预测评估结果。首先，MEMD-LSTM模型的各个预测性能指标均优于LSTM模型，其R2值提升了20.4%，表明MEMD能有效提取多维金融时序数据的特征，进而可提升区间交易量LSTM模型的预测性能。其次，M-LSTM模型的MAE、RMSE和R2优于MEMD-LSTM模型的预测结果，各项预测性能指标分别提升了3.8%、4.2%和3.5%，证实了注意力机制能显著提升和改善MEMD-LSTM模型的有效性和预测精度。此外，对比M-LSTM与动态因素分解预测、SVR和ARIMA三个对照模型的预测指标可知：对整个样本区间内日内交易量占比的预测而言，M-LSTM的预测精度优于上述三个模型。这些结果都表明M-LSTM是更有效的日内交易量分布预测方法。

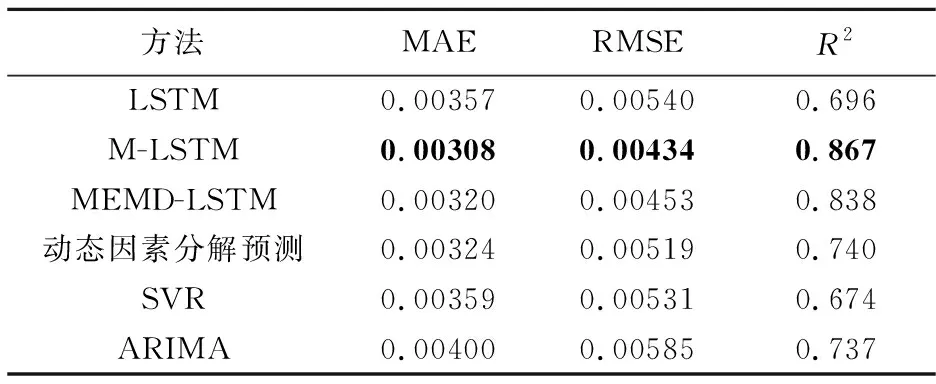
表3 各模型预测性能比较

3.2 不同走势阶段下M-LSTM的预测效果

股票指数在不同走势阶段下其价格、成交量等指标的波动特征存在明显差异，故本文进一步分析在指数不同走势阶段下，M-LSTM是否较现有预测方法更有效。根据上证指数在样本时间区间内所呈现的波动特征，将其划分为上涨、横盘和下跌3个阶段。划分过程中，将股市大幅度变化前后所引起股价“异常”波动的盘整阶段、股价上涨或下降周期过短的时间区间去除，阶段划分结果见表4。

表4 上证指数发展阶段划分

将各阶段数据集的前80%作为训练集，后20%作为测试集。由于各阶段数据量较少，为避免神经网络模型训练欠拟合，对各模型的超参数进行调整。根据不同参数组合设置下模型预测实验的对比结果，将LSTM预测模型的LSTM层设置为2层，上升、横盘、下跌状态下神经网络每层神经元个数分别设置为(10，10)、(10，10)和(20，20)，其余设置均保持不变。图6展示了上涨、横盘和下跌阶段下，模型对日内各区间交易量占比预测的平均绝对误差。在指数不同走势阶段下，M-LSTM的预测误差更小、效果更佳。表5～7中各模型对上证指数不同走势阶段下的日内成交量占比预测结果显示，M-LSTM的各项评估结果均优于5种对比模型，充分证实了在不同走势阶段下，M-LSTM对上证指数日内成交量分布的预测更有效。

图6 不同走势阶段下各模型的预测效果

表5 指数上升阶段各模型预测的评估结果

表6 指数横盘阶段各模型预测的评估结果

表7 指数下降阶段各模型预测的评估结果

3.3 更多典型指数的预测效果对比分析

为进一步验证M-LSTM对股票指数日内交易量占比预测的一般性和有效性，从聚宽量化平台提取2013/1/1至2020/5/1之间深证成指、中证500和沪深300三个典型指数的日内5分钟区间交易量多元时序数据，剔除缺失数据以及节假日因素，深证成指、沪深300指数均含有(1779×48)个数据，中证500指数含有(1778×48)个数据。将各指数交易量数据分别转换为48维的日内区间交易量占比时序数据，作为预测建模的初始输入。

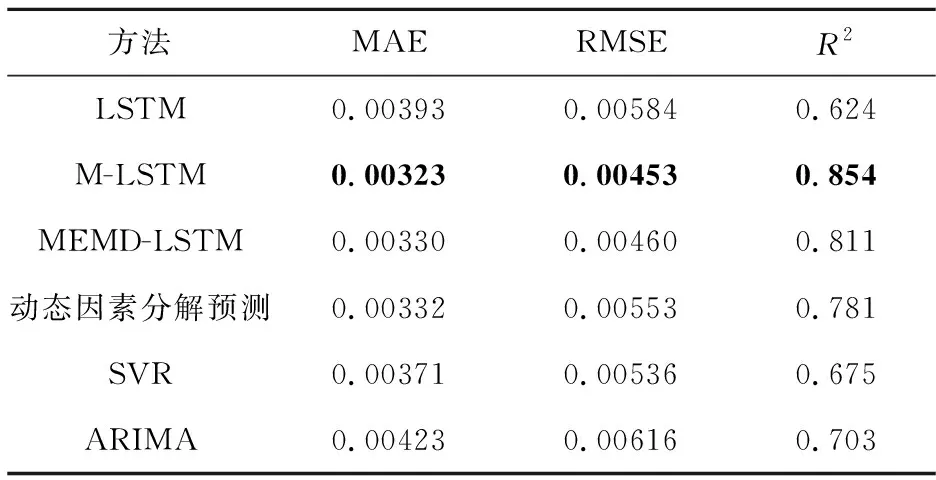
表8 各模型在深证成指上的预测性能比较

表9 各模型在中证500指数上的预测性能比较

表10 各模型在沪深300指数上的预测性能比较

参照上文所述M-LSTM建模思路，依次通过MEMD分解、高频去噪、重构及LSTM-Attention预测建模等过程，构建出上述3种指数对应的M-LSTM预测模型。同样采取滚动预测方式，分别运用ARIMA、SVR、LSTM、MEMD-LSTM和动态因素分解预测建模方法，构建各指数的预测对比模型，并采用MAE、RMSE和R2值作为预测效果的评价指标。表8～10给出了各模型对3种指数的日内交易量分布预测的评估结果，表明：与其余5个对比模型相比，M-LSTM的R2值最大，MAE与RMSE值最小，证实了M-LSTM模型对3种指数日内交易量分布预测的有效性和强适用性，故其能更有效地帮助投资者降低VWAP等相关策略的交易成本。此外，MEMD-LSTM的预测表现优于直接的LSTM预测模型，证实了对多维时序进行MEMD分解与重构可有效提升数据的信噪比，从而能间接提升模型预测性能。再者，M-LSTM的表现明显优于MEMD-LSTM，证实Atention机制能显著提升机器学习模型对多维金融时序的预测精度。因此，结合MEMD自适应分解功能、Attention有效筛选数据关键信息和LSTM提取长期时序依赖关系的优势，来构建日内交易量分布预测模型M-LSTM的思路是合理、有效的。

4 结论

股票指数日内交易量分布的高效预测对减少冲击成本、优化策略执行效果，具有重要的理论意义与实践价值。本文结合MEMD自适应分解多维时序信号的优点以及LSTM-Attention神经网络对多维金融时序数据预测准确度较高的优势，提出了一个面向日内交易量分布的集成预测模型M-LSTM。选取上证指数、深证成指等四个代表性股市指数近7年的交易量占比时序数据作为实验数据，在指数整体样本区间内以及不同走势阶段下，对M-LSTM、ARIMA、动态因素分解预测和SVR、LSTM等典型的交易量分布预测方法，进行系统的对比预测实验及分析。实验结果表明：相较于主流的多元金融时序预测模型，M-LSTM对股票指数日内交易量占比的预测误差更小、精度更高，预测效果明显提升，是一种更有效的股票指数日内交易量分布预测方法。同时证实，引入MEMD和注意力机制可提高多维金融时序预测建模的有效性。