考虑可信度和优先级的对偶犹豫模糊多属性决策在绿色审计中的应用研究

曲国华, 张潇丹, 曲卫华

(1.山西财经大学 管理科学与工程学院,山西 太原 030006; 2.山西财经大学 博雅学院,山西 太原 030012; 3.华北电力大学 经济与管理学院,北京 102206; 4.山西大学 管理与决策研究所,山西 太原 030006; 5.山西大学 经济与管理学院,山西 太原 030006)

0 引言

现如今经济正在飞速发展，城镇化、工业化的进程不断推进，信息技术的完善给我们带来便利，也会带来生态环境恶化等问题。作为环境污染源之一的企业，其排污或资源滥用等行为是使环境遭受破坏的直接诱因。因此，各国政府主管部门和企业管理部门必须制定相关的环境协议或法规加以规范，而提升和强化企业环境行为则是有效解决环境问题的关键途径之一[1]。企业环境行为是指企业对其生产经营过程中对环境产生不利影响的因素进行限制和控制的过程，特别是企业不当的环境行为会对环境造成潜在影响[2]。目前，也有许多关于企业进行环境行为评估及约束等方法提升经济效益的实践研究[3,4]。在企业环境行为分类体系中根据其具体表现，将企业环境行为分为绿色采购、绿色生产、环境技术创新等[5]。由于市场的多变性，许多企业在运行过程中面临着经济压力，绿色采购在企业经济压力中占据着较大的比重，而供应商的选择是物资采购的重要环节，也是采购部门的工作重心。

在选择供应商时，不仅要重视所提供的产品相关的问题，更要对供应商公司进行全面了解，尤其是目前生态环境问题严峻，为促进各国、各行业乃至消费者履行环保责任，企业选择的供应商必须有为保护环境与人类家园所做出贡献的具体行为，然而对供应商为环境做出的贡献进行量化并非易事。绿色环境审计为我们提出了新的思路，该方法能够降低各方的矛盾，促进社会的和谐绿色发展[6]。绿色环境审计是国家环境治理的重要监督机制，其工作包括环境污染防治绩效审计、环境污染防治资金管理和使用审计等[7]。绿色审计理应及时介入和实时跟进推进生态文明建设的全过程、全要素、全方位，对生态文明建设的管理系统、制度体系、项目资金、建设行为和业绩成效，独立、权威和专业地开展审计检查[8]。同时，绿色审计作为重要的环境监管手段，其环境治理作用愈发凸显[9]。可以采用政府环境监管的方式来对供应商的贡献进行审计，一方面可以保证其审计的客观性与公正性，另一方面，也可以为后续的供应商评测提供合理有效的参考依据。

随着经济全球化进程不断加快和社会分工进一步细化，供应链成员企业的数量越来越多，相互依存关系日益紧密，当决策者面对不确定的数据和情况时，迫切需要一个有效的模型来帮助决策过程评估相应的得分和供应商排名，以便采购经理对供应商做出合理的判断和选择。同时，在企业环境行为特点及绿色采购供应商的选择上，专家可信度和属性优先级起着重要作用，将两者结合创新出新的评价及选择方法并非易事，模糊数学的出现为解决此难题提供思路[10,11]。模糊数学随之成为研究热点，越来越多的专家学者发现对偶犹豫模糊集可以通过隶属度和非隶属度为决策者提供更多的信息，综合决策方法能提供很大的帮助。

Zadeh在1965年首先提出模糊集的概念，基于此，Atanassov在1986年提出了直觉模糊集，即增加了一个非隶属度来反映某元素对于某集合的非隶属程度。在此基础上，一些学者进行了扩充及推广[12]。杨洪尚[13]将算子引入对偶犹豫模糊集合中，提出基于对偶犹豫模糊语言变量集结算子的多属性决策方法，为后来的各类算子决策模型奠定理论基础；王金英[14]给出区间值对偶犹豫模糊集的各种距离测度的公式。各类研究均表明，对偶犹豫模糊集更具有研究价值。进一步地，Zadeh在模糊集中提出熵的概念后熵得到了广泛应用。此外，人们对于直觉模糊熵的研究在不断进行中，例如Zhao和Xu[15]研究了对偶模糊信息和直觉模糊信息熵测度的概念，给出相关熵的公式。与此同时，对偶犹豫模糊熵给决策者判断信息又增添了新的依据，目前国内外对于对偶犹豫模糊熵的研究成为热点，其研究成果不断增多[16～18]。Wang[19]提出了对偶犹豫模糊加权平均算子、几何加权平均算子及其在多准则决策中的应用。此后在模糊数学领域，各类算子的研究也更加深入[20,21]。文献[22]根据优先级的特性，首次提出了犹豫模糊集优先级加权平均和几何算子；文献[23]考虑根据可信度的特性，提出了研究可信度诱导犹豫模糊混合集成算子。文献[24]首次将可信度与优先级结合，提出考虑可信度和优先级的犹豫模糊可信度优先级混合平均和几何算子。

近年来，越来越多的专家学者开始考虑将模糊数学领域的专业方法及创新模型运用到实际生活当中，注重理论与实际相结合，提升理论方法的研究贡献[25,26]。例如，曲国华等人[27]以物流运作中供应商与第三方电商平台的双边公平匹配问题为导向，考察了区间对偶犹豫模糊信息双向投影技术下的双边公平匹配方法的有效性与实用性。李晓星等人[28]从企业环境绩效指标体系构建入手，提出了基于PSR框架的企业环境绩效审计指标体系，构建了结构熵权-模糊综合评价模型。在上述文献中，其研究内容的侧重点有所不同，将模糊数学领域的计算模型运用在绿色审计方面的研究较少，且同时考虑专家可信度和属性优先级的对偶犹豫模糊集成算子的相关成果仍不多见。

因此，本文在总结现有研究成果的基础上，将专家可信度和属性优先级融入到模型中，提出一种全新的决策方法。首先，由于决策者知识背景不同，对某些知识领域的熟悉程度也会存在差异，所以本文在对同一属性进行评价时，会分别给出对偶犹豫模糊集合中的隶属度与非隶属度相应的可信度，用来表示专家对属性的熟悉程度。其次，熵可以用来度量模糊信息的不确定程度，所以本文定义了考虑可信度的对偶犹豫模糊值的熵值算法，考虑到对偶犹豫模糊值与对偶犹豫模糊集之间的联系，又可将此公式推广到考虑可信度的对偶犹豫模糊集的熵值算法。再次，本文提出在考虑属性优先级并结合专家可信度的对偶犹豫模糊集合的多属性混合赋权算法，该赋权方法不仅能保证属性优先级恒定，还可以有效区分专家意见的统一程度以及专家对属性的熟悉程度，使评价方案更加合理客观。第四，在该混合赋权方法基础上给出两种犹豫模糊混合集成算子：对偶犹豫模糊可信度优先级混合平均(dual hesitant fuzzy confidence prioritized hybrid average, DHFCPHA)算子和对偶犹豫模糊可信度优先级混合几何(dual hesitant fuzzy confidence prioritized hybrid geometric, DHFCPHG)算子，并利用对偶犹豫模糊信息算子的运算规则研究了其优良特性。在此基础上，结合DHFCPHA算子和DHFCPHG算子构建了一类对偶犹豫模糊多属性决策方法。最后，以企业环境行为中绿色采购的供应商选择为例，融入绿色审计等评价指标进行案例分析及方案比选，验证此模型的可行性和有效性。

2 对偶犹豫模糊集基本知识

定义1[13]令X是一个固定的集合，在X上的对偶犹豫模糊集定义为：D={|x∈X}。式中，h(x)和g(x)是[0,1]中的两个集合，h(x)表示x∈D的可能隶属度，g(x)表示x∈D的可能非隶属度。称D(x)={h(x),g(x)}为对偶犹豫模糊元，简记为D=(h,g)。

性质1[12]∀γ∈h(x),∀η∈g(x)，γ+∈h+(x)=Uγ∈h(x),x∈Xmax{γ}，η+∈g+(x)=Uη∈g(x),x∈Xmax{η}，满足条件：0≤γ,η≤1,0≤γ+,η+≤1。

定义2[12]令D={|x∈X}表示一个对偶犹豫模糊集，h≠Ø,g≠Ø，则D的补集定义为：Dc={|x∈X}。显然(Dc)c=D成立。

定义3[12]设X为一固定集合，d1和d2是X上的两个对偶犹豫模糊集:

d1={|xi∈X,i=1,2,…,n}

d2={|xi∈X,i=1,2,…,n}

d1和d2的运算定义如下:

d1⊕d2={hd1⊕hd2,gd1⊕gd2}

{{γd1+γd2-γd1γd2},{ηd1,ηd2}}

(1)

d1⊗d2={hd1⊗hd2,gd1⊗gd2}

{{γd1γd2},{ηd1+ηd2-ηd1ηd2}}

(2)

(3)

(4)

其中，n≥0运算的结果也是对偶犹豫模糊集。

定义4[12]设对偶犹豫模糊集D={|x∈X}，则得分函数为:

其中，#h和#g分别表示h(x)和g(x)中元素的个数。

定义5[12]设d1和d2是论域X上的两个对偶犹豫模糊元，如果映射F:X→[0,1]满足以下四条准则：

(1)当d1=({0},{1})或d1=({1},{0})时，F(d1)=0；

(2)若hd1=gd1，F(d1)=1;

(3)当hd2(x)≥gd2(x)时，hd1(x)≥hd2(x)，gd2(x)≥gd1(x)，或者当hd2(x)≤gd2(x)时，有hd1(x)≤hd2(x)，gd2(x)≤gd1(x)。则F(d1)≤F(d2)成立；

3 基于对偶犹豫模糊熵值的优先级混合赋权方法

基于上述文章对于熵的基本知识的介绍，人们对于熵的应用也愈加广泛，这证明了熵对于决策事物的重要性和不可替代性，所以在本部分推导出考虑可信度的对偶犹豫模糊值的熵，并扩展推导出考虑可信度的对偶犹豫模糊集的熵。基于熵值公式，本节在考虑属性优先级并结合可信度的基础上提出对偶犹豫模糊集合的多属性综合赋值算法。

3.1 考虑可信度的对偶犹豫模糊熵值算法

对偶犹豫模糊集由隶属度和非隶属度两个部分组成，首先根据其的特性给出考虑可信度的对偶犹豫模糊值的熵值公式，考虑到对偶犹豫模糊值与对偶犹豫模糊集之间的联系，又可将此公式推广到考虑可信度的对偶犹豫模糊集的熵值算法。

3.1.1 考虑可信度的对偶犹豫模糊值的熵

设d={{γ1,γ2,…,γn1},{η1,η2,…,ηn2}}为一个对偶犹豫模糊值，那么其考虑可信度的隶属度，非隶属度和犹豫度指标分别定义为:

π(d)=1-h(d)-g(d)

下面给出对偶犹豫模糊值的熵的公式。

定理1对任意对偶犹豫模糊值d，设

则F(d)是考虑可信度的对偶犹豫模糊值d的熵。

3.1.2 考虑可信度的对偶犹豫模糊集的熵

考虑到对偶犹豫模糊值与对偶犹豫模糊集之间的联系，在定理1的基础上，我们可将此公式推广到考虑可信度的对偶犹豫模糊集的熵值公式。

定义7一个映射F:DHFS(X)→[0,1]称为对偶犹豫模糊集的熵，满足以下四条准则:

(1)F(D)=0当且仅当对∀i={1,2,…,n}，d=({0},{1})或d=({1},{0})；

(2)F(D)=1当且仅当对∀i={1,2,…,n}，hd(xi)=gd(xi)；

(3)对∀i={1,2,…,n}，当hd2(xi)≥gd2(xi)时，有hd1(xi)≥hd2(xi),gd2(xi)≥gd1(xi)；或者当hd2(xi)≤gd2(xi)时，有hd1(xi)≤hd2(xi)，gd2(xi)≤gd1(xi)。则F(D1)≤F(D2)成立；

(4)F(D)=F(Dc)。

定理2设D={|xi∈X}是论域X上的对偶犹豫模糊集

则F(D)是考虑可信度的对偶犹豫模糊集D的熵。

3.2 考虑可信度和优先级的对偶犹豫模糊综合赋权算法

在3.1中给出了考虑可信度和优先级的对偶犹豫模糊熵值算法，本节在考虑属性优先级并结合可信度的基础上提出对偶犹豫模糊集合的多属性综合赋值算法。

步骤1在专家的意见下，给出方案多个属性之间的优先级排序。

步骤2在计算出具有可信度的对偶犹豫模糊熵值f的基础上，根据下列公式判断相邻属性之间的重要性程度ri。

步骤3根据步骤2中计算出的重要性程度，按照下列所给公式确定优先级排在第c位的具体属性权重t0。

4 对偶犹豫模糊可信度优先级混合算子

第四部分中提及的对偶犹豫模糊综合赋权算法仅能对案例进行初步的熵值计算，本部分在上述基础上推导出DHFCPHA算子和DHFCPHG算子，混合平均算子和混合几何算子的引入会使案例计算更加精确直观。

4.1 对偶犹豫模糊可信度优先级混合平均算子

定理3若存在一组对偶犹豫模糊数F=(),∀γ∈h(x),∀η∈g(x),lj∈[0,1]表示与γj相应的可信度，kj∈[0,1]表示与ηj相应的可信度，则下式成立:

DHFCPHA

(1)

式中，tj(j=1,2,…,n)表示第j个属性的优先级混合权重。

定理4设存在一组对偶犹豫模糊数D=(),∀γ∈h(x),∀η∈g(x),若d1=d2=…=dn=d*，则有：

DHFCPHA(d1,d2,…,dn)=d*

d-≤DHFCPHA(d1,d2,…,dn)≤d+

定理6设存在一组对偶犹豫模糊数D=(),∀γ∈h(x)，∀η∈g(x),f=(θ,ρ)为对偶犹豫模糊数，则有:

DHFCPHA(d1⊕f,d2⊕f,…,dn⊕f)

=DHFCPHA(d1,d2,…,dn)⊕f

定理7设存在一组对偶犹豫模糊数D=(),∀γ∈h(x)，∀η∈g(x),若p>0，则有:

DHFCPHA(pd1,pd2,…,pdn)

=pDHFCPHA(d1,d2,…,dn)

定理8设dj(j=1,2,…,n)，fj(j=1,2,…,n)为对偶犹豫模糊数，且dj=(hj,gj),fj=(θj,ρj)，则有：

DHFCPHA(d1⊕f1,d2⊕f2,…,dn⊕fn)

=DHFCPHA(d1,d2,…,dn)⊕DHFCPHA(f1,f2,…,fn)

4.2 对偶犹豫模糊可信度优先级混合几何算子

定理9若存在一组对偶犹豫模糊数D=(),∀γ∈h(x)，∀η∈g(x),lj∈[0,1]表示与γj相应的可信度，kj∈[0,1]表示与ηj相应的可信度，则下式成立:

DHFCPHG(d1,d2,…,n)

(2)

式中，tj(j=1,2,…,n)表示第j个属性的优先级混合权重。

定理10设存在一组对偶犹豫模糊数D=(),∀γ∈h(x)，∀η∈g(x),若d1=d2=…=dn=d*，则有:

DHFCPHG(d1,d2,…,dn)=d*

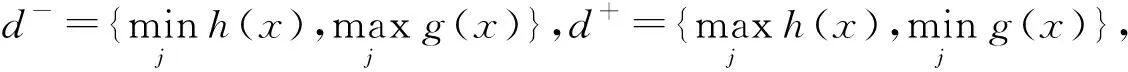
d-≤DHFCPHG(d1,d2,…,dn)≤d*

定理12设存在一组对偶犹豫模糊数D=(),∀γ∈h(x)，∀η∈g(x),f=(θ,ρ)为对偶犹豫模糊数，则有:

DHFCPHG(d1⊕f,d2⊕f,…,dn⊕f)

=DHFCPHG(d1,d2,…,dn)⊕f

定理13设存在一组对偶犹豫模糊数D=(),∀γ∈h(x)，∀η∈g(x),若p>0，则有:

DHFCPHG(pd1,pd2,…,pdn)

=pDHFCPHG(d1,d2,…,dn)

定理14设dj(j=1,2,…,n),fj(j=1,2,…,n)为两组对偶犹豫模糊数，则有:

DHFCPHG(d1⊗f1,d2⊗f2,…,dn⊗fn)

=DHFCPHG(d1,d2,…,dn)⊗DHFCPHG(f1,f2,…,fn)

5 基于DHFCPHA算子和DHFCPHG算子的多属性决策方法

基于本文提出的DHFCPHA算子和DHFCPHG算子，给出一种考虑专家可信度和属性优先级的对偶犹豫模糊多属性决策方法。假设方案集为A={A1,A2,…,Am}，属性集为G={G1,G2,…,Gn}，G1≥G2≥…≥Gn表示重要性程度(即优先级)逐级递减。因各个专家对于方案的熟悉程度不同，以及专家自身对方案属性的研究程度不同，在各专家给出方案属性的对偶犹豫模糊集的隶属度与非隶属度后，可以给出其相应的可信度来解决专家对于方案的熟悉程度及研究深度不同的问题。基于考虑专家可信度和属性优先级的对偶犹豫模糊信息集成算子的决策方法步骤如下。

步骤1利用定理2计算对偶犹豫模糊集熵值Fg(D)(i=1,2,…,m;j=1,2,…,n)。

步骤2计算基于对偶犹豫模糊熵值的优先级混合权重tij(i=1,2,…,m;j=1,2,…,n)。

步骤3采用DHFCPHA算子和DHFCPHG算子集成对偶犹豫模糊矩阵D=(dij)m×n，可得出对于方案Ai的综合表现值di(i=1,2,…,m)：

di=DHFCPHA(d1,d2,…,dn)

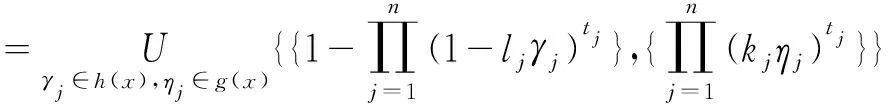
di=DHFCPHG(d1,d2,…,dn)

步骤4利用得分函数计算每个方案的总得分S(di)(i=1,2,…,m)。

6 实例与比较分析

6.1 实例分析

根据文献[5]对于企业环境行为特点的描述，建立绿色采购中供应商比选的评价指标体系需要考虑以下几点。首先，在选择供应商时，最重要的是供应商提供的产品质量。其次，企业要考虑供应商的经营管理能力，这是供应商的硬指标条件。第三，企业在选择供应商时要注意供应商的交货能力。最后，要考虑供应商的绿色环境审计结果，一个合格的供应商应该具备保护生态环境免遭破坏的社会责任。通过以上分析，参照企业环境行为模式分析及模型构建，本文可以建立一个较为全面有效的企业环境行为绿色采购供应商的选择模型，其要素可以分为产品质量指标、供应商运营指标、供应与交货能力指标和绿色审计指标。该案例内容为某公司需从所有供应商中选择四个合适的绿色供应商，经公司商议决定评选指标包括产品质量指标、供应商经营指标、供货能力指标和绿色审计指标。该公司通过专业筛选，找到在企业环境行为及绿色采购供应商选择领域具有公信力的专家评审组，该评审组中包含三位该领域的知名认证专家，来对供应商进行全面评估。经过对所有供应商的全面观察和了解，公司率先筛选出四家供应商来进行评选，三位专家可以根据各方的建议及自身对专业领域的熟悉程度来对四个属性进行评分。方案A代表四个不同的供应商，结合供应商选择的四个属性，将属性集G表示为产品质量指标、供应商经营指标、供货能力指标和绿色审计指标。在匿名评估中，三位专家给出每个方案对每个属性G的评估值A。评价值包括隶属度和非隶属度两部分。同时，专家给出相应的可信度数据，剔除完全重复的数据，形成基于对偶犹豫模糊信息的决策矩阵，如表1所示。以上述步骤为纲，整合数据来评估和选择哪个绿色供应商更适合本公司。

表1 对偶犹豫模糊决策矩阵

据步骤计算出各方案的得分情况为S(d1)=4822,S(d2)=0.4721,S(d3)=0.401,S(d4)=0.3994。则由总得分情况可知，S(d1)≥S(d2)≥S(d3)≥S(d4)，由定义4可知，总得分值越大，则对应的方案越优，故在此次测评方案中，为最佳方案选择。

6.2 对比实例分析

本部分利用文献[24]中的算法进行分析对比，将表1中的对偶犹豫模糊集合中隶属度作为犹豫模糊数，并对应其各集合中隶属度所给的可信度，矩阵如表2所示。

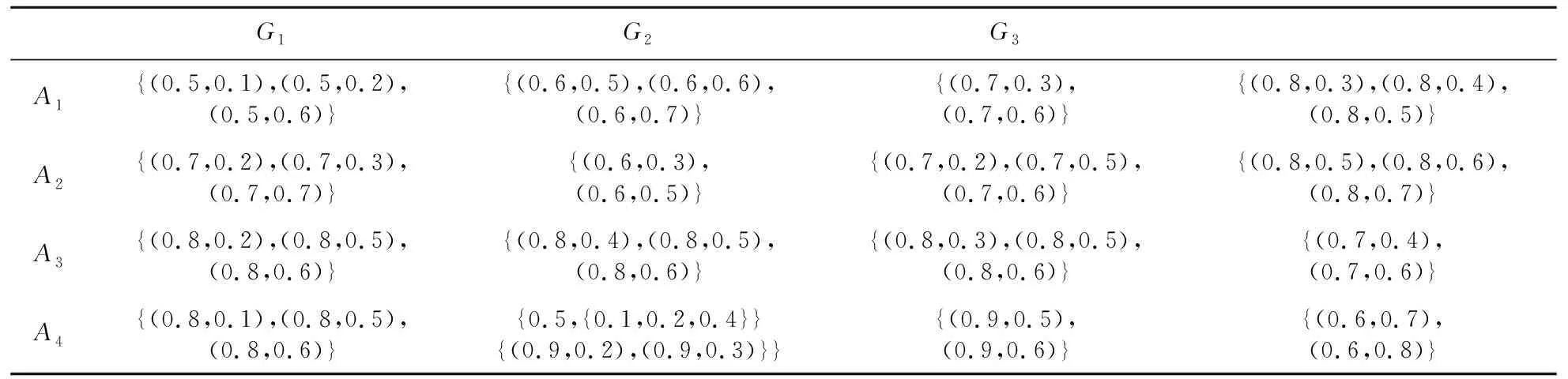
表2 犹豫模糊决策矩阵

采用文献[24]中的HFCPHA算子及HFCPHG算子进行信息集成计算优先级混合权重，并利用总得分函数计算各方案得分情况：S(h1)=0.5162,S(h2)=0.4583,S(h3)=0.4832,S(h4)=0.4224。则由总得分情况可知，S(h1)≥S(h2)≥S(h3)≥S(h4)，根据总得分函数性质，在此次测评方案中为最佳方案选择。

6.3 同已有文献比较分析

文献[24]中所提的HFCPHA算子和HFCPHG算子所得到的排序结果与本文算例得到的结果完全一致，所选择的最优候选方案都是A1，客观上反映了本文方法的一致性和稳定性。其方案的排序却有不同，从方案2和方案3的数据对比可知，方案2中非隶属度值对于熵值的计算结果有一定影响，重要性占比较大，而利用犹豫模糊集的模型默认对于方案及属性仅存在隶属度，故而本文提出了DHFCPHA算子及DHFCPHG算子。

同时，两种在计算过程中均考虑了专家的可信度以及属性的优先级和多属性权重的多方面影响，同时所用到的两种信息集成算子具有较好的区分度和稳定性。本文方法通过专家可信度和属性优先级进行赋值计算，在原有方法基础上增加了属性优先级的影响因素，将传统决策中的属性由主观判断转化为客观数据，优化了对偶犹豫模糊集的熵值计算公式，使熵值考虑范围更加严谨，并在此基础上提升多属性决策方案计算结果的准确程度。

7 结语

本文提出的多属性决策方法中包含对偶犹豫模糊集的隶属度和非隶属度，并在该方法中融入专家的可信度和属性的优先性，考虑了决策者的更多信息可以根据实际情况进行多重评价。同时，将对偶模糊犹豫、熵算法和信息集成算子等概念相结合，将专家可信度和属性优先级作为新的扩展，然后将该方法应用于企业环境行为及供应商选择领域，并在多属性决策模型中加入绿色审计的评价指标。与现有方法相比，本文提出的对偶犹豫模糊信息集成算子不仅考虑了企业环境行为及各属性领域专家的熟悉程度，而且绿色审计指标的运用使得该决策方法适应现如今环境治理和绿色监管方面的政策要求，使供应商等相关企业对于生态环境的重视程度加大。本文多属性决策模型的缺点是只考虑了部分重要属性的优先级，要想将所有影响因素的指标属性全部放入数学模型的方法还有待探索和发现。本文提出的方法可以应用于各个领域，特别是需要考虑专家意见和属性重要性的决策，如宏观经济计划的选择和公司绩效评价。