多拱联合受力结构体系的研究与应用*
2022-11-10苏恒强欧阳秋李雨盈
苏恒强,欧阳秋,李雨盈,何 军,何 岸
(1 广东省建筑设计研究院有限公司, 广州 510010;2 华南理工大学土木与交通学院, 广州 510641)
0 引言
钢拱结构的设计主要包括承载力、稳定性以及刚度三方面[1],由于拱的受力特性是以受压和受弯为主,钢拱结构表现出的稳定问题较为突出和复杂,常常是钢拱结构设计的控制因素[2]。目前,已有众多学者针对拱式结构体系展开相关研究,罗赤宇等[3]提出高层建筑大跨度拱架结构的概念;周桂林等[4]提出一种拱转换结构;王振等[5]通过考虑初始几何缺陷和双重非线性的全过程分析方法对一次张拉V形腹杆内凹式索拱结构进行静力稳定性参数分析;孟永杰等[6]介绍了一种由主拱、后拱及次桁架组成的大跨空间拱结构;纪晗等[7]针对呼和浩特汽车客运东站的建筑造型特点提出了组合拱的结构形式;余洋等[8]分析了一个复杂双曲面落地拱结构体系的静力特性、动力特性以及整体稳定性;董越等[9-10]对高矢跨比索拱结构的力学性能进行了研究,并提出一种柔性撑杆的弦撑式索拱结构。
虽有学者针对实际工程问题提出了不少拱式结构体系,但目前对合理设置结构构件使钢拱结构形成一个在平面内外均能较大程度上实现自平衡的结构体系鲜有研究及应用。本文以新疆哈密市民服务中心项目为研究背景,提出一种多拱联合受力结构体系,如图1所示,并对其进行分析研究。
1 工程概况
新疆哈密市民服务中心项目的抗震设防类别为重点设防类(乙类),抗震设防烈度为7度,设计基本地震加速度值为0.1g,设计地震分组为第二组,建筑场地类别为Ⅱ类,基本风压为0.7kN/m2,基本雪压为0.3kN/m2,屋面附加恒载标准值为1.5kN/m2,活载标准值为0.8kN/m2,结构最大正温差取45℃(升温),最大负温差取40℃(降温),钢结构阻尼比为0.02。
在新疆哈密市民服务中心项目中采用的多拱联合受力结构体系如图2所示,其主要由主拱、次拱、水平卧拱、水平桁架、腰桁架及预应力拉梁组成,主拱长方向跨度约为110m,拱高约为26m,次拱尺寸为φ700×22,水平卧拱尺寸为φ500×30,其他主要构件的尺寸如表1所示。

表1 主要构件尺寸
多拱联合受力结构体系如图2所示。内倾的双主拱通过水平桁架和次拱相连接,水平桁架和次拱为双主拱提供平面外支撑,且内倾的双主拱可抵消次拱产生的部分拱脚推力,水平卧拱则将两侧翼的水平推力传至腰桁架和主拱处,同时腰桁架可抵消部分水平卧拱的拱脚推力,此外,主拱平面内产生的绝大部分拱脚推力由腰桁架和预应力拉梁抵消,从而较大程度上实现结构自平衡、自稳定的目的。
2 各方案主拱稳定性分析对比
在使用MIDAS Gen软件进行屈曲分析时,结构发生屈曲时的临界荷载等于初始荷载乘以屈曲荷载系数,初始荷载不宜设置过大以防结构在初始荷载作用下已发生失稳,因此在稳定性分析对比模型中将1.1kN/m的线荷载作为初始荷载施加于主拱上弦杆上,主拱各弦杆采用铰接支座。模型中杆件截面均与工程实际尺寸相同,材料采用Q345钢材。在非线性屈曲分析中,同时考虑初始几何缺陷、几何非线性及材料非线性,采用Mises屈服准则,屈服强度为3.45×105kPa,不考虑硬化。初始几何缺陷根据结构第一模态以及结构最大节点位移为主拱跨度的1/300确定。进行非线性屈曲分析前,先进行弹性受力分析,确定在荷载作用下位移最大的节点,在非线性屈曲分析中,以控制该节点位移的方式进行加载,最后,通过荷载-位移曲线的下降点来确定结构的极限承载力。
各方案的第一阶弹性屈曲模态如图3~6所示,前几阶弹性屈曲模态的失稳形式如表2所示。在单主拱的情况下,由于平面外缺少约束,平面外刚度较弱,故第一、二阶弹性屈曲模态均为平面外失稳,第三阶才出现平面内失稳。带腰桁架的单主拱的前三阶弹性屈曲模态均为平面外失稳,平面内弹性屈曲模态出现较晚,第四阶才出现平面内失稳,由此可见,腰桁架增加了主拱平面内的刚度,但此时仍缺少平面外约束,导致主拱平面内外的刚度相差较大。带次拱的双主拱和带次拱及腰桁架的双主拱的第一、二阶弹性屈曲模态为平面外失稳,第三阶弹性屈曲模态为平面内失稳,说明两主拱间水平桁架和次拱的设置为主拱提供了平面外约束,增加了主拱平面外的刚度,缩小了主拱平面内外的刚度差距。
各方案前几阶弹性屈曲模态的荷载系数及失稳形式如表2所示。由表2可见,各方案第一阶平面内失稳的弹性屈曲荷载系数均大于第一阶平面外失稳的弹性屈曲荷载系数。带腰桁架的单主拱的前几阶弹性屈曲荷载系数均大于单主拱,且平面内失稳的弹性屈曲荷载系数增加较多,说明腰桁架的设置使主拱平面内外的稳定性均得到提高,且平面内的稳定性提高程度大于平面外。与单主拱和带腰桁架的单主拱相比,带次拱的双主拱的前三阶弹性屈曲荷载系数均有所增加,分别为单主拱的2.83、2.07和1.26倍,平面外失稳的荷载系数增加较多,说明在两主拱之间布置连接桁架及次拱后,主拱平面外稳定性显著增强。带次拱及腰桁架的双主拱的前三阶弹性屈曲荷载系数分别为带次拱的双主拱的1.07、1.19和1.16倍,说明腰桁架的设置使双主拱平面内外的稳定性均得到了提高。由此可见,在弹性屈曲分析中带次拱及腰桁架的双主拱的稳定性最好,腰桁架、次拱、水平桁架等结构构件的设置可提高主拱平面内外失稳的弹性屈曲荷载系数,且对平面外失稳的弹性屈曲荷载系数的提高程度更多,同时还能使平面内失稳和平面外失稳的弹性屈曲荷载系数趋向接近,即使主拱平面内外刚度趋向接近。

表2 各方案的弹性屈曲荷载系数及失稳形式
各方案的非线性屈曲变形如图7~10所示,主拱的最大位移均发生在斜率较小处,其中单主拱和带腰桁架单主拱的非线性屈曲为平面外失稳,与弹性屈曲第一阶模态相同,带次拱的双主拱和带次拱及腰桁架的双主拱则与弹性屈曲第一阶模态不同,为平面内失稳。由图11可见,在非线性屈曲分析中,单主拱的位移为-0.845m时,荷载系数达到最大值65.4,为弹性屈曲荷载系数的17.5%;带腰桁架的单主拱的位移为-0.792m时,荷载系数达到最大值69.4,为弹性屈曲荷载系数的16.7%,为单主拱非线性屈曲荷载系数的1.06倍;带次拱的双主拱的位移为-0.5m时,荷载系数达到最大值181.5,为弹性屈曲荷载系数的12.7%,为单主拱非线性屈曲荷载系数的2.78倍;带次拱及腰桁架的双主拱的位移为-0.45m时,荷载系数达到最大值193,为弹性屈曲荷载系数的11.5%,为带次拱的双主拱的非线性屈曲荷载系数的1.06倍。由此可见,考虑初始几何缺陷、几何非线性及材料非线性后四种方案的结构极限承载力均有较大下降,其中带次拱及腰桁架的双主拱的极限承载力最大,带次拱的双主拱次之,单主拱最小。
综上所述,通过设置腰桁架、次拱、水平桁架等结构构件能提高结构的极限承载力,其中设置水平桁架和次拱将两主拱联系在一起对提高主拱极限承载力影响最大,设置腰桁架可有效提高主拱的平面内刚度。
3 钢桁架非对称拱内力分析及措施
由于主拱外形的不对称,在竖向荷载作用下,构件内力亦不对称,因此,根据拱轴线上轴力、弯矩的分布,主拱采用变截面桁架。在实际工程中,主拱在恒载+活载作用下的轴力如图12所示,拱脚轴力相差较大,A端杆件最大轴力约为9 200kN,B端杆件最大轴力约为16 000kN,约为A端最大轴力的1.74倍。针对这种情况,在设计中A、B两端的桁架弦杆采用不同的截面:A端弦杆的最大截面为φ1 000×30,B端弦杆的最大截面为φ1 250×32。考虑到经济性,防止B端弦杆截面过大,在B端靠近拱脚的弦杆内灌注C40混凝土,形成钢管混凝土弦杆,大大提高了弦杆的抗压承载力及稳定性,在满足结构安全性的前提下,减小了杆件的尺寸,取得了良好的经济效益。
4 侧翼抗侧力方案对比
由于结构两侧翼纵向(X向)的跨度大并存在斜率约为0.16的坡度,侧翼上的恒载和活载会引起较大的水平推力。此外,由于实际工程处于新疆哈密地区,风荷载、昼夜温差大,四季气温变化剧烈,在温度变化和风荷载作用下沿侧翼纵向(X向)的水平推力也较大。因此,如何抵抗水平推力,使得结构杆件的内力和变形均处于满足规范要求的合理范围内并具有清晰的传力途径和经济效益成为结构设计的一个关键点。
采用三种侧翼抗侧力方案进行对比,方案一为无卧拱及侧翼水平桁架方案(图13),方案二为在两侧翼端部增设侧翼水平桁架方案(图14),方案三为在两侧翼端部增设卧拱方案(图2),其中方案二的侧翼水平桁架腹杆截面采用HW350×350×12×19,方案三的腰拱采用截面φ500×30的圆钢管。为直观反映结构侧向刚度与卧拱和腰桁架构件之间的关系,在侧翼末端作用一列大小为1 000kN的模拟节点水平荷载,验算其在水平荷载作用下的结构内力和位移。
表3为各抗侧力方案的力学性能及经济性对比。由表3可见,方案一的腰桁架跨中杆件轴力最大值最大,方案三比方案二增加了4.6%,说明方案三与方案二在此方面相差不大,均可作为备选方案。方案一两翼端部跨中的侧向位移(主拱下腰桁架的跨中侧向位移)和腰桁架端部弦杆内力最大,方案二次之,方案三最小,其中方案二和方案三的两翼端部跨中侧向位移分别为方案一的64%和58%,方案二的腰桁架端部弦杆内力远大于方案三,约为方案三的2.1倍,说明在控制两翼端部跨中的侧向位移和腰桁架端部弦杆内力中方案三的效果最好。

表3 各抗侧力方案的力学性能及经济性对比
方案三在水平荷载作用下的杆件轴力如图15所示,方案三中卧拱拱顶处的轴力为1 628kN,两翼主梁的轴力约为550kN,卧拱的轴力远大于两翼主梁的轴力,且方案三中两翼主梁的轴力比方案一减少约373kN,表明卧拱的设置可有效抵抗水平推力。由表3可知,方案二和方案三中腰桁架端部杆件与跨中杆件的轴力最大值比值分别为3.85和1.75,可见方案三的腰桁架内力分布更为均匀,因此方案三的抗水平力性能优于方案一和方案二。
同时,在两翼端部跨中侧向位移基本相同的前提下,方案三比方案二的用钢量少(表3)。并且,方案三中的卧拱有效地使水平力“跨越”水平桁架,直接作用到作为支座的主拱上,避免了水平桁架在作为主拱拉杆的同时,还要抵抗很大的侧翼传来的水平力,造成双向受力的不利情况,这是同样具有可观的抗侧刚度的水平桁架方案所不具备的优越性。此外,卧拱杆件数量少、截面轻盈,可减轻结构自重,同时卧拱方案的节点数量少,结构形式简洁,降低了节点施工量,建筑使用阶段的观感也比较良好,具有可靠的结构安全性和较高的经济性。
综上所述,侧翼水平桁架和卧拱的设置均能显著增加结构的侧向刚度,而方案三较为经济且受力更均匀、传力途径更简洁清晰,因此两侧翼的抗侧力方案宜选择方案三。
5 卧拱刚度与结构侧向刚度的关系研究
综上可知,在两侧翼端部设置卧拱具有良好的抗水平力性能和较高的经济性,对卧拱刚度和结构侧向刚度的关系进行研究有助于确定在哪些具体条件下,增大卧拱刚度可显著减小两侧翼端部跨中侧向位移(腰桁架跨中侧向位移),从而以优化后的结构布置得到较好的效果。
卧拱按照受压杆件设计,可认为杆件刚度K=EA/L,由于弹性模量E与杆件长度L为定值,可通过改变杆件截面面积A来改变卧拱的刚度。选取以下六种卧拱截面进行研究:φ450×15(A=0.020 5m2)、φ500×30(A=0.044m2)、φ800×30(A=0.072 6m2)、φ1 000×30(A=0.091 4m2)、φ1 300×40(A=0.015 83m2)、φ1 500×40(A=0.183 5m2)。
卧拱截面面积与两侧翼端部跨中侧向位移的关系曲线如图16所示。当卧拱截面面积A小于0.091 4m2时,两侧翼端部跨中侧向位移随卧拱刚度的增大而减小较快,而当A大于0.091 4m2时,关系曲线的走势逐渐趋于平缓,其原因是结构的抗侧刚度由卧拱和两翼框架共同决定,卧拱与两翼框架相互支承,若仅提高卧拱的刚度,而两翼框架的刚度保持不变,则卧拱刚度的提高对总体结构侧向刚度的提高的效率会逐渐降低。因此,采用卧拱体系来提升结构侧向刚度时,需要注意卧拱与两翼框架的刚度协调才能取得良好效果。
6 吊杆作用分析
由于主拱下方的腰桁架跨度长达78.8m,在两侧翼的竖向荷载作用下,如何控制腰桁架跨中杆件的内力和挠度亦是设计的一个关键点。
通过在主拱和腰桁架之间是否设置吊杆,对比主拱与腰桁架的内力和变形,以研究在竖向荷载作用下吊杆对减少结构变形和增加结构冗余度的贡献,吊杆的设置情况如图2所示。
以1.35恒载+1.4×0.7活载作为竖向荷载代表值,吊杆采用13组2φ245×12钢管,忽略两翼混凝土结构对钢结构的支承作用进行分析。
两种情况的结构变形如图17所示,可见增加吊杆可有效减小腰桁架的变形。表4为设置吊杆前、后腰桁架的力学性能对比。由表4可知,腰桁架的下弦杆轴力和挠度在设置吊杆后均大幅下降,其中下弦杆轴力最大值减小了4 200kN,挠度减小了285mm,即由跨度的1/192减少到1/630,已满足规范[11]变形容许值(跨度的1/400)的要求,说明吊杆的作用是在腰桁架跨内增加了支点,减少了腰桁架计算跨度,从而减小腰桁架的变形及杆件内力。

表4 设置吊杆前、后腰桁架的力学性能对比
7 整体分析
结构在各种工况下的竖向位移最大值如表5所示。竖向位移包络最大值为199.62mm,满足规范[11]跨度的1/400的要求。在升、降温工况下的最大竖向位移分别为63.25mm和63.32mm,可见温度作用对结构的影响不可忽略,在设计中应考虑。此外,结构杆件的应力比最大值为0.96,小于1.0,满足承载力要求。
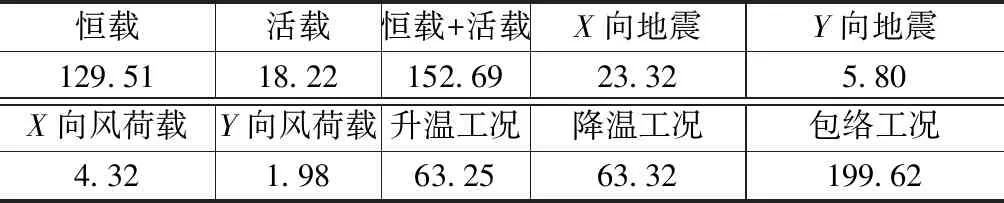
表5 各种工况下竖向位移最大值/mm
8 结论
(1)多拱联合受力结构体系采用多个钢拱结构与桁架相结合,在两榀相互内倾的钢主拱之间设置水平桁架、次拱、腰桁架等结构,使两主拱的极限承载力及平面内外稳定性得到了较大提高,一定程度上实现了结构自平衡、自稳定的目的,且受力状态更加合理。
(2)由于主拱外形的不对称,其构件内力亦不对称,通过在主拱左右两侧采用不同截面的桁架杆件及在轴力较大的拱脚处设置钢管混凝土弦杆的措施可有效提高主拱的安全性和经济性。
(3)在两侧翼抗侧力方案中创新性地采用水平卧拱抵抗大跨度斜面结构的水平推力,结果表明效果显著,且需要注意卧拱与两侧翼框架的刚度协调才能有效发挥水平卧拱的抗侧力性能。
(4)在主拱与腰桁架之间设置吊杆可减小腰桁架的计算跨度,对减小腰桁架的竖向位移和杆件内力有显著作用,且可为腰桁架提供杆件截面优化的空间。
(5)该结构体系在各工况下的位移满足规范要求,杆件应力比满足承载力要求,且温度作用对结构有较大影响,在设计中应考虑温度因素的影响。
