迁移算理 沟通算法
——以“多位数乘一位数口算乘法”教学为例
2022-11-10浙江余姚市更大小学315400童奎魁
浙江余姚市更大小学(315400)童奎魁
数学课程标准关于运算能力的解释为“能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题”。可见,学生不仅要会算,还要懂得为什么这样算,也就是计算教学目标中常说的掌握算法和理解算理。那么,如何让学生掌握算法的同时理解算理?如何在一堂课中处理好算法和算理的关系与教学比重,使二者达到一个平衡?面对这样的要求和问题,笔者以三年级上册“多位数乘一位数口算乘法”的教学为例,谈谈对计算教学的一些想法。
【教学片段1】
出示例1:坐碰碰车每人20元,3人需要多少钱?
师:你从题目中知道了哪些数学信息?需要解决什么问题?
生1:每人20元。3人需要多少钱?
师:能列出式子吗?
生2:20×3。
师:计算结果是多少?
生3:60。
师:是怎么算出来的?
生4:20+20+20=60。
师:理由是什么?
生5:根据乘法的意义,20×3就是3个20相加。
师:还有其他办法吗?
生6:先算2乘3等于6,再在6的末尾添0。
师:其中的2是什么意思?为什么还要在末尾添0?
师(出示小棒):1捆小棒有10根,可以看成1个十,20根就需要2捆小棒表示,也就是2个十。现在这样的小棒有3份,有6个十,就是60。原来这里的2就是2个十,2个十乘3就等于6个十,就是60。
师:200×3呢?该如何计算?
生7:2个百乘3等于6个百,就是600。
师:2000×3呢?
生8:2个千乘3等于6个千,就是6000。
【评析:对于“20×3”,学生知道怎么算,但不知道为什么这样算。教师利用小棒进行梳理,根据小棒列出算式,总结出简单的说理句式“2个十乘3等于6个十,就是60”,让学生在模仿中理解算理。接着,教师给出几个十、几个百再到几个千乘一位数,引导学生迁移算理去掌握新知。】
【教学片段2】
出示例2:坐过山车每人12元,3人需要多少钱?
师:如何列式?
生1:12×3。
师:结果是多少?
生2:36。
师:试着用学具摆一摆,在草稿纸上画一画、写一写。
生3(方法1):12+12+12=36。根据乘法的意义,将乘法算式12×3转换成12+12+12,得到36。
生4(方法2):10×3=30,2×3=6,30+6=36。通过摆小棒,用1捆小棒与2根小棒表示12,这样的有3份,3捆小棒就是10×3=30,有30根。同样的道理,2根小棒也有3份,2×3=6,有6根。最后把它们合起来是30+6=36,有36根。
生5(方法3):(10+2)×3=36。
生6(方法4):
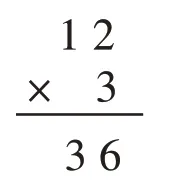
师:请将这四位同学的方法分分类,并说出理由。
生7:方法1是一类,方法2、3、4是一类。方法1是利用加法运算,其他都是把12拆成10和2后分别乘3,然后相加。
【评析:皮亚杰曾说:“儿童的思维是从动作开始的,如果切断动作与思维的联系,思维就得不到发展。”可见动手操作对学生学习知识的重要性。在“12×3”的教学中,教师提供小棒和计数器供学生操作,在学生充分体验和感知的基础上,再让学生在纸上画一画图、列一列式子。由动作表征到图像表征,再到符号表征,学生有充足的交流空间,他们的思维在碰撞中产生智慧的火花——知道算法虽然多样,但本质是相同的。】
【教学片段3】
练习1:神秘的宝塔
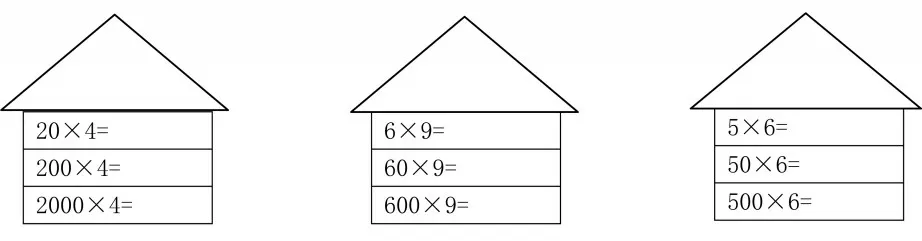
练习2:口算

练习3:小卖部里每瓶矿泉水2元,买24瓶矿泉水需要多少钱?
【评析:这里给出了三个层次的练习。第一个层次:既有两个数相乘不进位的,也有两个数相乘进位的;学生在完成练习的过程中总结出“去0→相乘→添0”的算法;两个数相乘,且进位后末尾有0的练习,是为了让学生发现相乘后的0和添上去的0是不同的。第二个层次:通过比较200×7与700×2发现“算式不同,但结果相同”,究其原因是在算2个百乘7和7个百乘2时都是用“二七十四”这一句口诀。第三个层次:解决生活中的实际问题,让学生感受到数学与生活的紧密联系。】
【教学感悟】
本教学紧紧围绕“学生是学习的主体,教师是学习的组织者、引导者与合作者”的教学理念,较好地实现了课前的预想。学生始终能保持一种积极进取的良好状态参与到学习中并学有所成。见微知著,通过“多位数乘一位数口算乘法”这课的教学,笔者对计算教学有了更深的认识。
一、创设情境,激发兴趣
数学源于生活,生活是数学生长的土壤。教师要将教学内容与学生熟悉的生活场景联系起来,以提升学生的学习兴趣和利用计算解决问题的欲望,拉近学生与数学知识之间的距离,增强学生数学学习的主动性。如本课创设的游乐园的情境,符合学生爱玩的年龄特点;练习3中贴近生活的小卖部买水的情境,容易使学生共情。情境是佐料,可以让学生学习计算更有“味”,但计算终归要回到实际应用中,不然就成了无水之源、无本之木。
二、纵向迁移,清晰算理
算理是计算过程中的道理,是指计算过程中的思维方式,是用来解决为什么这样算的问题。而迁移在心理学中指的是一种学习对另一种学习的影响,指在一种情境中获得的知识、技能或态度,对另一种情境中知识、技能的获得和态度形成的影响。迁移算理,要求学生能举一反三、触类旁通,将之前所学的计算过程中的思维方式用到将要解决的问题中,并能把问题解决。
学生在学习本课之前已经知道2×3=6,计算20×3时,学生能直接写出60,没有思考过程,完全靠直觉,谈不上什么迁移:先算2×3=6,接着在6的末尾添上0就是60。虽然计算结果是正确的,但没有理解计算过程。在本课中,笔者没有过早地让学生寻找规律“计算出积,再看因数末尾有几个0,就在积的末尾添上几个0”,而是引导学生想得更清晰、更全面、更合理:用小棒来表示20×3,通过小棒让学生理解是2个十乘3等于6个十,就是60,所 以 要 在6的 末 尾 添 上0;通 过200×3以 及2000×3,让学生将刚掌握的几十乘一位数的算理迁移到几百、几千乘一位数的算法上。12×3的教学是20×3算理的深度迁移,学生通过操作小棒和计数器,知道12可以分成1个十和2个一,先算3个十,10×3=30,再算3个2,2×3=6,最后算30+6=36。不会迁移算理就谈不上理解算理,虽然不可能让所有学生在一节课内理解算理,但可以让学生在理解算理的路上走得更长久一点,让学生的思维发展得更多一点。
三、横向沟通,理法相融
算法是在理解算理的基础上概括出的普遍计算法则。解决问题的算法是多样的,学生提出的算法往往有异曲同工之妙,教师要沟通联系这些算法,给学生呈现最本质的东西。通过算法之间横向的沟通联系,让学生透过现象看本质,掌握解题策略。
计算练习往往给人以枯燥乏味的印象,对此,教师设计练习要有针对性、有层次性,更要有趣味性。可以借用多媒体或者学具、教具让学生进行试算、口算和抢答,也可以由教师出题或者学生出题后进行计算竞赛。练习1中的“5×6,50×6,500×6”这一组题就凸显了学生的计算易错点——容易把算出来的0和添上的0搞错。练习2中的“200×7,700×2”这一组题的算理细看还是有不同的。算理是算法的理论依据,算法是算理的凝练概括。只有通过练习,使算理与算法互相交融,达到一个平衡,学生才能对二者有一个深度的把握。
综上,教师在教学时不能靠生搬硬套,而应该以学生的理解为前提,算理与算法的教学齐头并进,促使学生拥有完整的计算能力。
