培育符号意识需重视数学化中的意识进程

四川成都市龙泉驿区教育科学研究院（610000）郑大明

一、符号意识在数学化中的心理和行为进程

从数学教育的角度来看，数学学习的过程就是人脑对客观现实进行数学化的过程。荷兰数学家弗赖登塔尔指出，数学化是一个过程，只要现实世界在一系列因素的影响下进行着变化、延拓和深化，这个过程就在持续，这也包括数学。特莱弗斯在教育脉络内明确了两个形态的数学化观点——水平和垂直的数学化。因此，可以说“水平数学化涉及从真实世界走入符号世界，而垂直数学化则是在符号世界内前进”。

感知是人的感觉器官接受信息的过程，而意识是人脑对感官获得的信息进行处理的结果。因此，意识既是大脑处理信息的行为，也是大脑处理信息所获得的结果。可以认为，符号意识是伴随着人的心理发展和信息处理行为而生长变化的（如表1）。

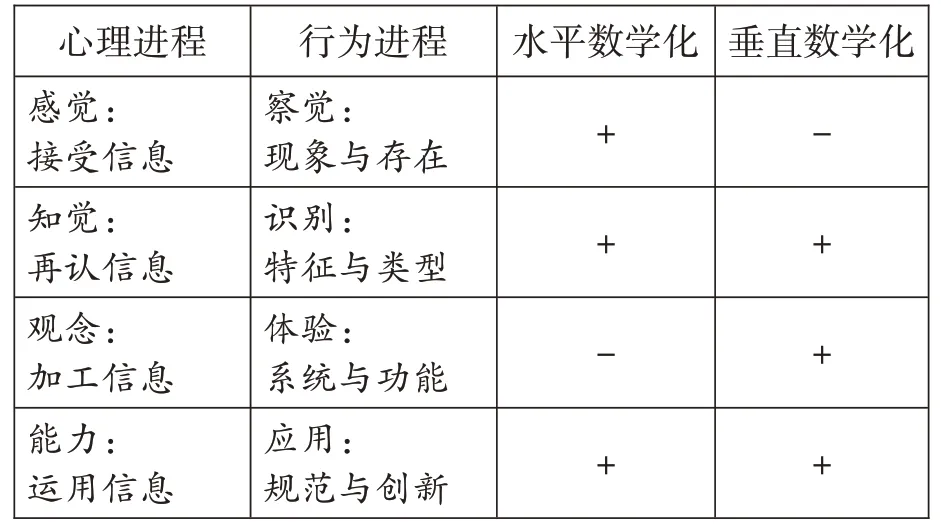
表1 符号意识与心理、行为进程的关系

科学家认为，意识有先天进化的基因意识和后天习得的素养意识之分。有些意识是显露出来的可以传播和交流的意识流，有些意识是隐藏在灵魂深处的无法传播和交流的，即潜意识。于是有人把这些意识分为本我意识——进化而来的本能性意识，自我意识——掺入主观认知的素养性意识，超我意识——融入群体交流和大众传播以后的社会性意识。

鉴于意识本身的综合性与复杂性，可以把数学素养中的符号意识看作是基于自我意识和超我意识的特殊形态。因为数学符号是记录、交流、传播数学知识的工具，是数学认知、表达和应用的语言系统（如表2）。

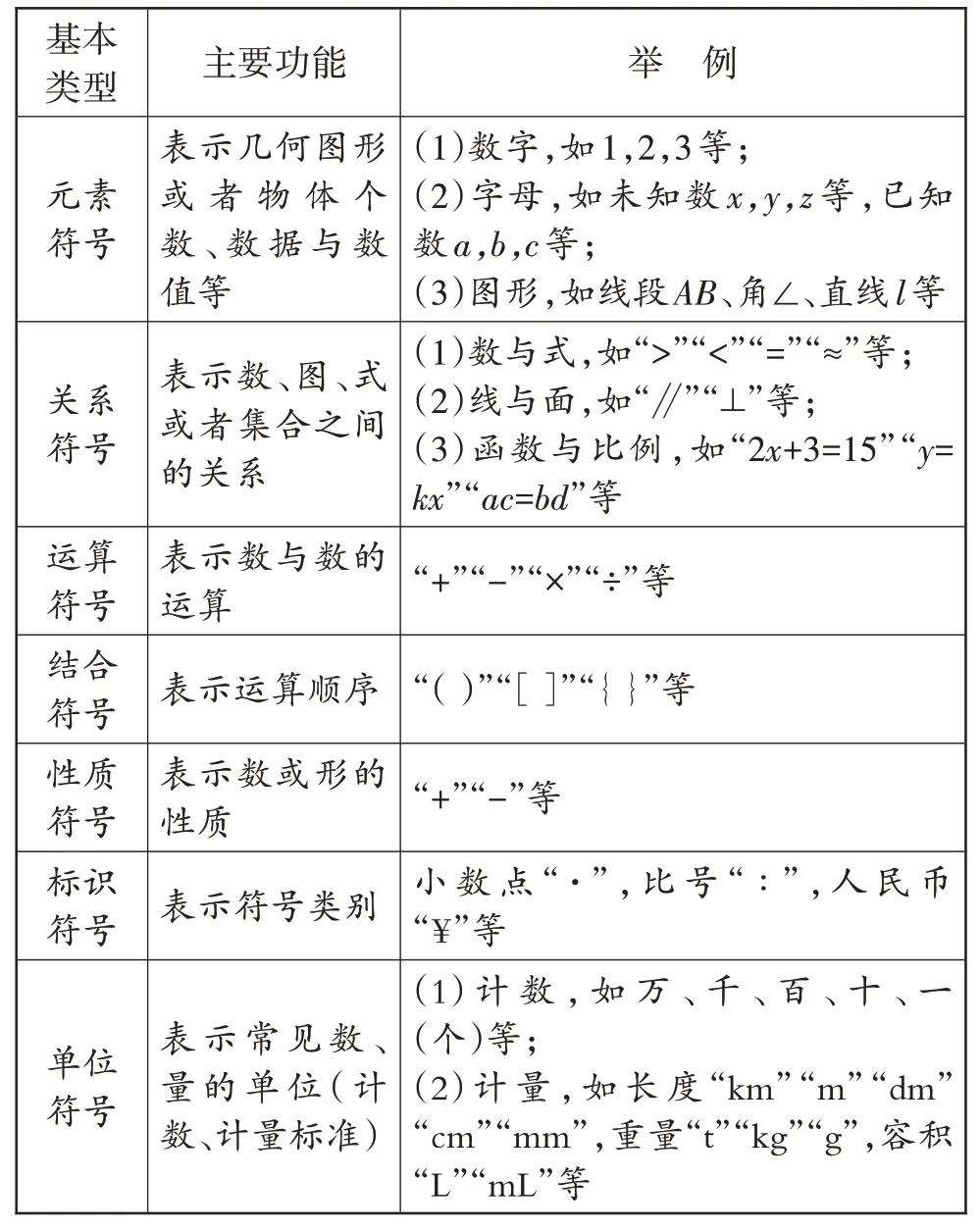
表2 数学符号的基本类型和主要功能

续表

二、在水平数学化中完成符号的感觉与知觉过程

水平数学化，是通过信息互动实现数学现实和数学符号相互连接的关键环节。

1.感觉情境中的符号，是意识符号现象与存在的前哨

感觉，是人体的感觉器官接受外界刺激的心理行为。这种心理行为使得我们认识现实世界和接受外界信息成为可能。因此，行为心理学家的“刺激—反应”学习论，就在符号学习中发挥着前哨性作用。

（1）交流中感觉符号。在交流中，让学生讲述生活的经历或者有趣的故事，就会涉及元素、单位等符号。比如家里有“5个人”，吃了“3顿饭”，吃了“8颗糖”，见到“2只小猫”等，这些都有数学符号的影子。因此，数和量的讲述很容易让学生意识到数学符号的存在。

（2）观察中感觉符号。在生活中，无论是无意识还是有意识的观察，都能看到许多图形、文字、标识等与数学相关的符号。比如碗筷、桌凳、毛巾、广告牌等。“圆形的碗”“方形的桌子”“1双筷子”等符号信息，都能刺激学生的视觉、听觉和触觉。因此，在教学一些基本的数学符号之初，教师就要有目的地组织学生进行观察。

（3）交易中感觉符号。购物就是货币与实物之间的符号联系的过程。比如一个物品的单价、几个物品的总价、付钱与找钱等，即使是数字化支付，也是学生感觉符号的数学功能的重要情境。又如买2块橡皮、3张卡纸、4盒牛奶、2米长的皮筋等，学生从中还能感觉到整数、小数等不同的数学符号，感觉到大小、多少、同样多等抽象的词语符号。

（4）阅读中感觉符号。要认识标准的、规范的数学符号，数学阅读是最佳途径。尽管数学符号简约抽象且难认难读，但在阅读中查阅资料和请教老师、同学，就能丰富自己的数学符号信息库。特别是中高年级的学生，要认识代数式、运算公式、关系式、统计表图等数学符号，系统的阅读是必不可少的。因此，教师从低年级起就要培养学生的阅读习惯，让他们在自觉和不自觉中感受数学符号。

（5）综合实践中感觉符号。在家庭、社会以及学校组织的相关活动中，要让学生意识到数学符号的作用和价值，并能体会和理解数学符号的重要性。比如节日购物活动、春游活动、校园模型制作、太空旅行畅想、垃圾处理调查等，学生都能接触到大量的数、量、形的符号，以及表示运算、关系的符号。教师要认真研究这些活动于如何让学生意识到数学符号的作用和价值，给出合适的学习任务和评价方式。

2.知觉情境中的符号，是意识符号特征与类型的中枢

知觉，是大脑指挥感觉器官主动感知外界刺激的心理行为。当感觉器官接受了外界刺激后，大脑就会对外界事物进行反向知觉。因此，认知心理学家的信息“识别—加工—控制”学习论，就在符号学习中发挥着中枢性作用。

（1）知觉交流中的符号。在交流活动中，先安排学生聆听他人言语中有关数学符号的内容；接着让学生进行信息的识别、加工和记忆；最后要求学生复述，其他学生可以补充和解释。比如讲“给家人摆碗筷”时，可以让学生“从1到几”一个一个地复述怎么摆；讲“来了几位客人”时，可要求学生说出“几位男客人、几位女客人”“是男客人多，还是女客人多”等，促使学生体会这些符号的特征。

（2）知觉参观中的符号。在参观活动中，要求学生画一画、写一写、说一说，不但在看到的符号上留下印迹，汇报时还要采用多种形式展示。比如方形的广告牌、圆形的摩天轮、球形的气球等，要求学生把“分别有多少”“谁多谁少”等讲清楚，这样有利于他们在了解符号特征的基础上能够区别类型。

（3）知觉交易中的符号。要求学生在交易活动中记住交易中的钱币、货物的数量等，主动观察或索取小票、账单、菜单、收据、货单等；汇报时分别说明钱币符号、数量符号、日期符号等。学生对不同类型的事物和现象需要不同的符号表达，从而对符号有一个初步的认识。

（4）知觉阅读中的符号。数学阅读是识别、加工、掌握数学符号的关键途径。因此，应让学生阅读后，通过填表、填图等方式主动分类记录和抄写看到的数据、图形、单位等符号，并能区分运算、结合、关系等不同类型的符号。特别是像“∠”“⊥”“○”等简约符号以及括号、小数点、循环点、进退位点、分数线、比号、正负号等应用广泛而又容易混淆的符号，更要加以重视。

（5）知觉综合实践中的符号。在综合实践活动中，学生只有沉浸于现实情境，才能真正理解数学符号与数学现实的真正联系。教师必须仔细研究每一次活动所涉及的符号的特征、类型、作用等，提供给学生最佳的探究的内容、时机、方式等。比如“校园模型”制作项目活动，涉及数、量、形符号的特征、类型、用途、价值等，教师要重视活动方案的细节设计，这样才能促使学生完成识别、加工、掌握数学符号的知觉任务，获得好的学习效果。

三、在垂直数学化中完成符号的体验与应用过程

在意识进程中，水平数学化只让学生认识了现实世界与符号世界的关联事实。而数学的语言体系是一个不断向纵深发展的符号系统，教师只有清楚整个数学化过程才能完成教学（如图1）。

图1 数学现实与数学符号的数学化过程

数学的语言体系与数学的思维方法、应用功能有着同等的地位。新修订的《义务教育数学课程标准（2022年版）》一再强调教材的“整体性、层次性、结构性、一致性”，就是要求教师关注数学语言系统的垂直数学化问题，即在水平数学化沟通了数学与生活的联系以后，学生必须利用已有的数学知识基础进行深度学习，形成系统化、结构化的认知。

1.在抽象与推理中获得体验，是意识符号系统与功能的关键

（1）在现实情境中获得符号体验。数学的现实情境包括生活与学习现实。如“数人数”时，很多学生会把自己漏掉，原因是他们看到什么数什么，没有“从自己起”和“从零起”的“位置数”概念。因此，他们容易理解“1，2，3，4……”，而对“0，1，2，3……”的数法较难理解。因此，很多教材让学生认识“0”的时候，不是用“数数法”而是用“减数法”，例如“3条鱼，小猫吃完了就是0”。这样一来，遇到“余数为0”和“-1，0，+1”的“0”时，学生就搞不清楚了。对此，教师要让学生先记住自己的位置是“0”，再数“1，2，3，4……”。对于“小明左边有3名同学，右边有4名同学”这一情境，学生在计算时就会加上“小明的位置”而得到“3+1+4”的结果了。

（2）在模拟情境中获得符号体验。许多抽象的关系符号，比如“大于、小于、等于”“倍、分、比、等式、比例”等，需要学生在模拟情境中获得认知体验。通过“真人表演”“学具拼摆”“图画记录”“举例子类比”等方式，学生对数据及其相互关系等进行对比、归纳，得出“a＞b，a=b，a＜b，an=b，b÷n=a，a∶b=n”等符号系列和“当c不为0时，有‘a+c＞b+c，ac=bc，a-c＜b-c，（a÷c）n=b÷c，（bc）÷（nc）=a，（ac）∶（bc）=n’”等情况。

（3）在虚拟情境中获得符号体验。在中高年级的数学中，大数、小数和分数以及相应的长度、面积、体积等都会进入“再认识”阶段，“千以内的数”“厘米、毫米、分米”“小数和分数的初步认识”等，都无法直观地靠数、量、画的办法体会，很难靠思维、想象与推理得出其数学意义。但是，计算机模拟系统就可以轻而易举地通过数字编程实现“叠加”和“细分”，直观地展示虚拟情境。

2.在迁移与应用中进行实践，是意识符号规范与创新的高地

（1）在后续学习中使用符号。很多数学符号的功能，都是学生在后续学习中慢慢体会出来的。比如“0占位”和“小数点位移”，都是在计算“2×3，20×3，20×30……”“0.2×3，0.2×0.3，0.02×0.3……”等的过程中，学生才真正体会到“0”和“.”的作用。学生在低年级认识m、dm、cm、mm时全靠记忆，在中年级使用km、hm以后，才慢慢地发现“m”前面的“d”表示“1个单位的十分之一”，“k”表示“1个单位的1000倍”等。于是，学生就在课外阅读中明白了“30 mg”“5 kg”“100 MB”“256 GB”的真实意义，从而意识到每一个数学符号的规范性和严谨性。

（2）在问题解决中使用符号。数学符号是根据人们的需要不断升级、不断系列化的。在解决问题的过程中，比如遇到“数大数和分小数”“量大物和量小物”等问题时，学生会发现之前学习的计数和计量单位不够用，必须要启用或者创造新的数学符号。比如，教了1平方厘米和1平方分米以后，要求学生测量操场的面积，学生就觉得无奈：这么大的操场，怎么测量呀？他们就会想到要用上更大的测量单位，也就会根据已掌握的1厘米、1分米、1米，得出1平方米、1平方十米、1平方百米、1平方千米的想法。

（3）在实践创作中使用符号。当前非常提倡以“项目式学习”为代表的跨学科综合实践活动。因此，教师可以设计一些简单的创作项目，以帮助学生使用和创造数学符号。比如，前面提到的“校园模型”制作活动就可以打造为项目式学习活动。学生可以先拍照、画画、测量、估测等，也许还要计算和设计图纸，或是购买纸板、胶泥等材料。他们除了用到已有的知识，还会创造出一些自己不曾学过的东西。不管是设计测量、计算，还是购物中的哪个方案，都会涉及数学符号的功能、作用、价值等，也许还有我们意想不到的“可遇而不可求”的新东西出现！