直管在横向流体冲刷下的流固耦合分析
2022-11-10梁铁波王昌朔廖成宇
姜 超 梁铁波 王昌朔 廖成宇 艾 阳
(中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610213)
0 引言
流致振动广泛存在于管壳式热交换设备中,流体冲刷传热管所造成的流致振动会对直管结构造成等幅循环载荷,且振动次数较大。当振动累积的疲劳损伤值达到传热管材料的临界疲劳损伤值时,传热管就会发生破损。因此传热管的流致振动特性分析可为其使用寿命的预测提供参考。
近年来,随着计算流体力学(CFD)技术的发展,国内外许多学者针对流体冲刷直管引发的流致振动现象做了很多研究。Williamson等人通过圆柱的涡激振动实验,发现了2S、2P、2C之后第四种引起涡激振动的周期性漩涡尾流模式2T,这种模式是在每半个周期内形成三个漩涡,并且所有这些尾流模式都是反向对称的。K.Lam等人基于表面涡模型和流固耦合方法,研究了低雷诺数横流作用下的管束振动特性。陈德奇等人基于欧拉-伯努利梁理论,采用动网格技术,通过Fluent和Transient Structural实现带格架5×5燃料棒束的双向流固耦合计算,对其振动特性进行模拟研究。冯志鹏等人采用双向流固耦合方法,并结合动网格技术对直管在内流、外流和内外流共同作用下冲刷直管的瞬态模拟计算,得到单向耦合与双向耦合下直管的振动轨迹。乔永亮等人针对三维圆柱绕流问题,研究不同的湍流模型对计算精度的影响。赵颖杰等人在Workbench中用CFX和Transient Structural计算模块对蒸汽发生器传热管的直管段进行了汽液两相双向热流固耦合数值分析。徐枫等人采用数值方法,分别模拟了圆柱体和多种棱柱体在横向流动中的流致振动现象,得到横向和流向位移随时间的变化曲线,研究发现圆柱中心的振动位移路迹大致为“8”字型。但目前针对不同的湍流模型对流致振动特性分析的研究还较少。
因此本文基于双向流固耦合方法,针对不同的湍流模型,对直管在横向流体冲刷作用下的流致振动特性进行了研究。结合不同流速工况下管中心位置的振动幅值及振动频率,确定一种精度较高的流固耦合计算方法。
1 数值模型
对横流冲刷直管的流致振动模拟,是建立在双向流固耦合的基础上,本研究采用Transition SST模型、Realizable k-e模型、低雷诺数k-e模型和LES模型分别对流体流动进行描述。
1.1 Transition SST模型
Transition SST四方程转捩模型,是将SST kω两方程湍流模型与另外两个转捩模型方程进行耦合,其中一个输运方程描述转捩流动的间歇因子γ,另一个方程描述从层流过渡到湍流的起始条件。
其中,SST k-ω关于湍流动能k和耗散率ω的输运方程式为:
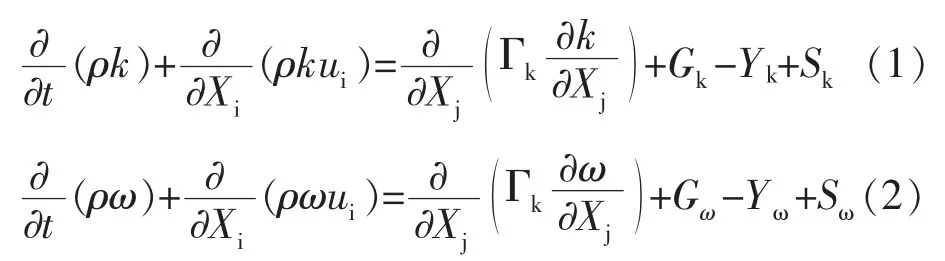
式中,G和G分别为k和ω的增量;分别为Γ和Γ的扩散系数;Y和Y分别为湍流引起的k和ω的耗散;S和S分别为k和ω的自定义源项。
其中,描述转捩流动间歇因子γ的输运方程式为:
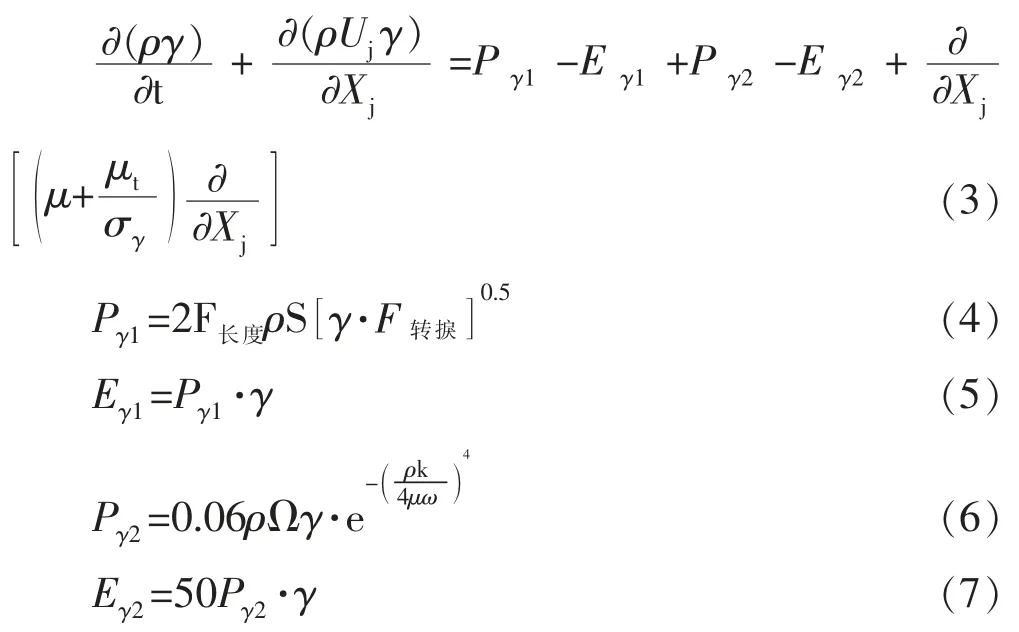
式中,S为应变速率的大小;Ω为漩涡强度;F为涡量雷诺数Re和动量厚度雷诺数Re的函数。
其中,描述转捩开始位置的动量厚度雷诺数Re的输运方程式为:

式中,y为沿法线方向到壁面的垂直距离。
1.2 Realizable k-e模型
Realizable k-e模型中,湍流动能k和耗散率ω的输运方程为:
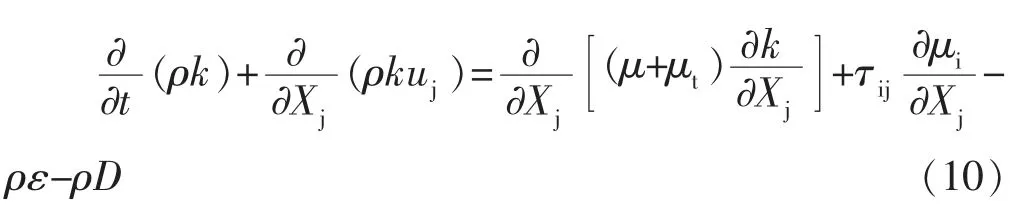
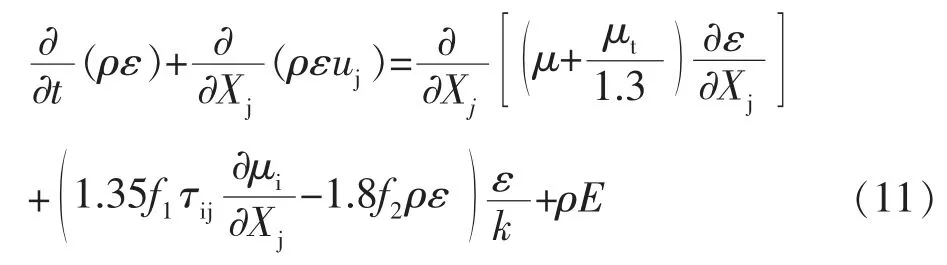
式中,μ为涡流粘度;f和f为阻尼系数;D和E分别为湍流动能k和耗散率ω的源项。
1.3 低雷诺数k-e模型
低雷诺数k-e模型的湍流动能k和耗散率ω的输运方程与Realizable k-e模型形式相似,不同的是低雷诺数k-e模型中涡流粘度不是常数:

式中,C为常数;f为阻尼函数。
1.4 LES模型
LES模型是利用滤波的方法,对于大尺度的涡采用直接数值模拟求解,而对于其余各向同性的小尺度涡流则可用亚网格尺度模型采用雷诺平均方法进行求解。
动量方程形式如下:
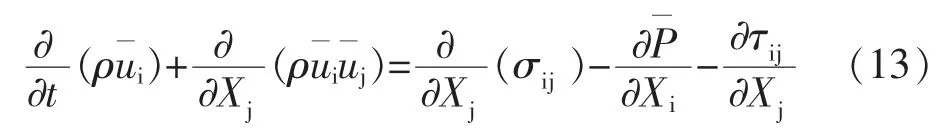
湍流应力张量表示亚网格尺度的应力:
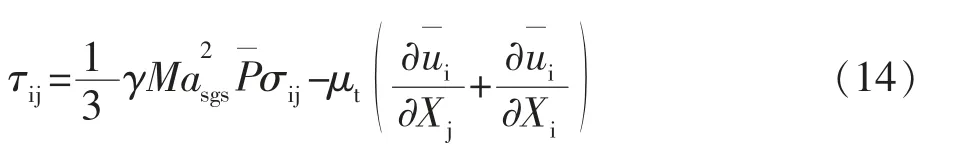
式中,μ为亚网格尺度下的湍流粘度;σ表示两个正交单位向量的点积;Ma为亚网格尺度下的马赫数。
2 物理模型及边界条件
2.1 物理模型
数值计算的模型参数与David Schowalter的试验参数保持一致,直管与流场的尺寸参数详见表1。直管轴向与流场的长和高垂直,直管圆心到流体进口的距离为50mm,高度也是50mm,几何模型如图1所示。
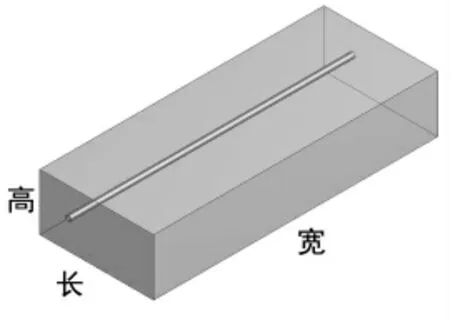
图1 几何模型示意图
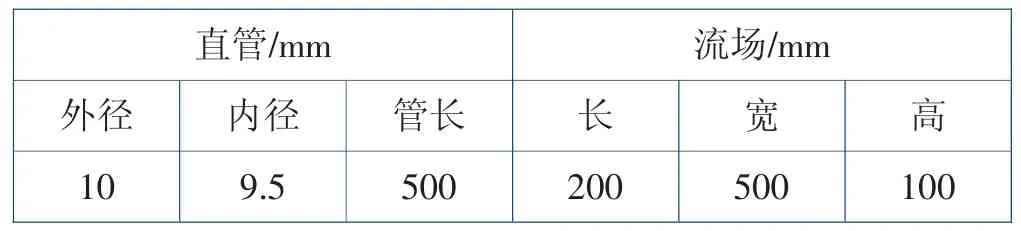
表1 直管与流场的尺寸参数
2.2 边界条件
对于直管流致振动问题的数值求解,流场的入口类型为“速度入口”,出口类型为“压力出口”。David试验中所采用的无量纲流速u:

式中,无量纲流速u的取值范围为1~6;u为来流速度;f为直管的一阶固有频s率;d为直管的外径。
在稳态流场计算的基础上进行结构的静力学分析,然后再进行模态分析,得到直管固有频率。直管的一阶固有频率f为173.6Hz。根据公式(15)可得试验中来流速度u的范围为1.74~10.42m/s,因此本文将入口流速范围取为3~7m/s。
3 数值模型计算
3.1 流致振动特性计算
基于ANSYS Workbench平台,采用动网格技术和双向流固耦合计算方法,研究直管在3~7m/s流速范围内的横向冲刷下的流致振动特性,得到直管中心点沿来流方向(x方向)和垂直来流方向(y方向)上的振幅以及振动频率。
以3m/s工况为例,进行网格无关性验证计算。采用不同湍流模型,经流固耦合计算得到的直管中心点振幅及振动频率。由网格无关性验证计算可知,当网格数量增加至8.6万时,Realizable k-e模型得到数值解不再随网格数量变化;当网格数量增加至17.5万时,低雷诺数k-e模型得到数值解不再随网格数量变化;当网格数量增加至26万时,Transition SST和LES模型得到数值解不再随网格数量变化。
经过数值计算,得到不同湍流模型在3m/s来流速度下直管中心点的位移轨迹,并得到直管中心点在x和y方向上的振动幅值及振动频率。位移轨迹如图2所示。
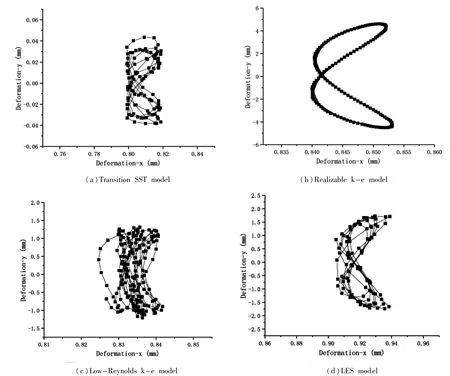
图2 直管中心点的位移轨迹
综合以上四种湍流模型在3m/s流速工况下流致振动的计算结果,发现采用Realizable k-e模型和LES模型计算振动更易达到收敛,得到的振动幅值也更加稳定。在3m/s流速工况下,直管的振动特性参数与David试验值的对比详见表2。

表2 直管振动特性参数
3.2 湍流模型适用性分析
此外,本文还选取4m/s、5m/s、6m/s和7m/s的入口流速,分别进行了流固耦合计算,得到不同工况下的直管流致振动特性。直管中心点在x、y方向上的振幅以及振动频率见图3~图5。
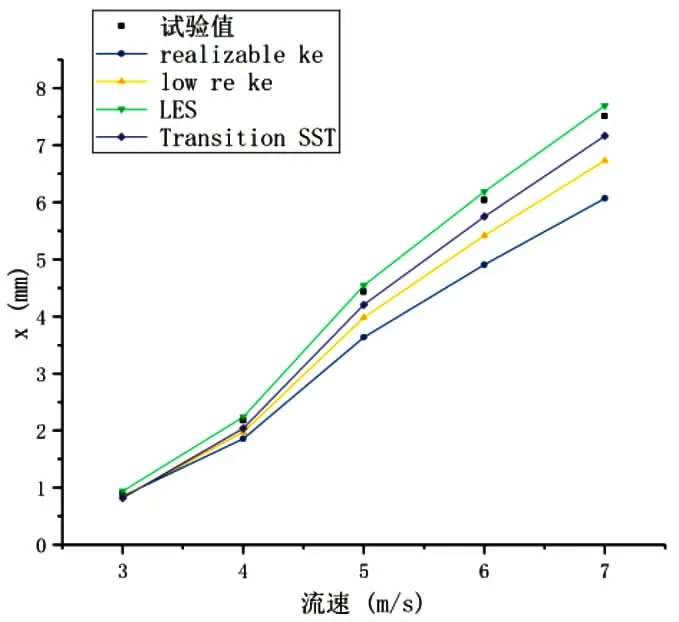
图3 直管在x方向上的振幅
由图3和图4可知,在3~7m/s的流速范围内,采用LES和Transition SST模型计算得到的直管中心点在x方向的振幅与试验值最为接近,与试验值之间的偏差分别为3.08%和10.11%;采用LES模型计算得到的直管中心点在y方向的振幅与试验值之间的偏差最小,与试验值之间的偏差为4.19%,而其他三种湍流模型显然无法准确模拟出直管在y方向的振幅。
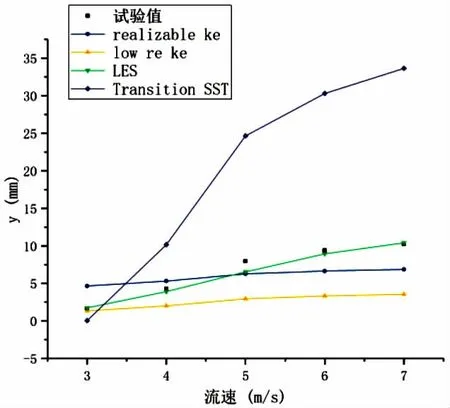
图4 直管在y方向上的振幅
由图5可知,在3~7m/s的流速范围内,采用LES模型模拟得到的流致振动频率最接近试验值,与试验值之间的偏差在1.51%以内。
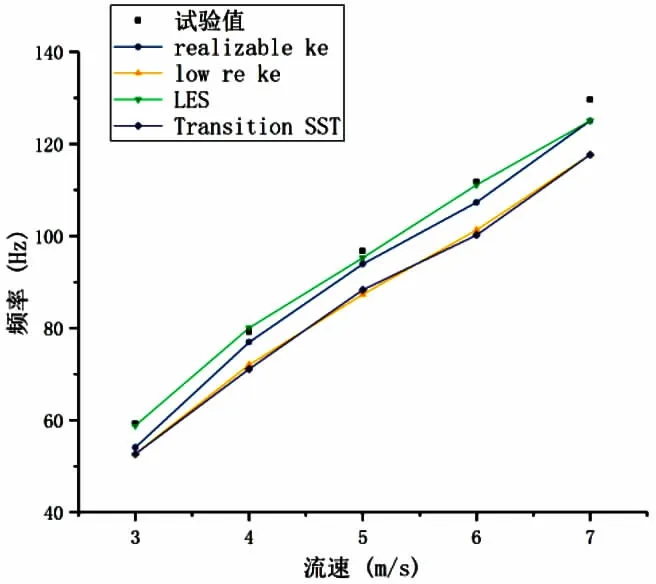
图5 直管的流致振动频率
4 结语
本研究采用四种不同的湍流模型,在3~7m/s流速范围内,分别进行流体横向冲刷直管的流固耦合计算,得到直管的流致振动特性。通过与试验值对比分析,得出结论如下:
(1)在3~7m/s流速范围内,在流固耦合计算中,流场的湍流模型选择LES模型能更好地模拟直管在横流冲刷下的流致振动,得到的x、y方向上的振幅最接近试验值,且偏差在5%以内;
(2)在3~7m/s流速范围内,LES模型对流致振动频率的模拟最准确,其次为Realizable k-e模型。
本研究认为,在3~7m/s流速范围内,LES模型能更好地模拟直管在横流冲刷下的流致振动问题,耦合计算得到的振动幅值与试验值之间的偏差小于5%,振动频率与试验值之间的偏差小于2%,但更广范围内的适用性,仍需进一步的验证。
d:直管的外径
f:直管的一阶固有频率
