近视患者SMILE术后人工晶状体度数计算公式精确性比较
2022-11-09徐欢欢马飞
徐欢欢 马飞
从2011年近视小切口基质透镜取出术(small-incision lenticule extraction,SMILE)开始上市到现在,全球已经有150万近视患者接受了SMILE手术[1],而且随着全球近视患者的增长,SMILE手术量也在不断地增加。这部分SMILE术后的患者不久的将来就到了需要行白内障手术的年龄。往往这些患者对白内障手术效果的期望较高,希望能够获得更加完美的术后视觉效果。目前对于SMILE术后白内障人工晶状体计算公式的研究还比较少。本研究就目前应用于准分子激光原位角膜磨镶术(laser in situ keratomileusis,LASIK)和屈光性角膜切削术(photorefractive keratectomy,PRK)术后人工晶状体计算公式中较为精确的3个公式进行研究,比较该公式在SMILE术后人工晶状体度数计算的精确性。
资料与方法
一、对象
前瞻性病例对照研究。选取2020年1~6月在我院行近视SMILE手术的患者60例(60只眼),选取患者右眼为研究对象,其中男性30例,女性30例,年龄(21.6±1.7)岁(19~25岁)。入选标准:(1)矫正视力≧1.0;(2)球镜度数<-8.00 D;(3)柱镜度数<-3.0 D;(4)术前2年内屈光度数稳定;(5)SMILE手术顺利。排除标准:(1)矫正视力<1.0;(2)眼部病变、泪膜异常、眼位异常、眼球震颤、黄斑偏中心注视;(3)斜视、弱视、圆锥角膜、其他感染性角膜疾病及眼部手术史。
本研究遵循《赫尔辛基宣言》的要求,受试者均签署知情同意书并经东部战区总医院伦理委员会批准。
二、方法
所有患者均进行SMILE术前常规检查,包括:裸眼视力、主觉验光、角膜地形图检查、角膜检查。显然验光分别测量SMILE术前、术后的等效球镜,等效球镜的差值为SMILE手术引起的屈光误差(SMILE-dif)。假设所有患者均植入爱尔康SN60WF单焦点人工晶状体。用于人工晶状体度数计算的A、A0、 A1和 A2 常数,分别为118.9、1.839、0.400和0.100。
采用IOL Master 500 (Carl Zeiss Meditec AG)中的Haigis公式,设定目标屈光度为0计算SMILE术前人工晶状体度数。Pentacam HR(OCULUS Optikgerate GmbH)分别测量术后3个月的角膜曲率、眼轴长度、前房深度、晶状体厚度、HWTW长度。SMILE术后人工晶状体度数计算使用美国白内障与视光手术协会(American Society of Cataract and Refractive Surgeons,ASCRS)网站(https://ascrs.org/tools/post-refractive-iol-calculator) 上的屈光术后人工晶状体在线计算中的Shammas、Haigis-L,Barrett True K公式。计算与SMILE术前相同度数人工晶状体的目标屈光度,该目标屈光度为人工晶状体引起的屈光误差(IOL-dif)。IOL-dif与SMILE-dif的差值为预测误差(prediction error,PE)。按照术前等效球镜度数将研究对象分为A组(≤-3 D)27只眼,B组(>-3 D)33只眼,分别比较A、B两组PE结果。
三、统计学分析方法

结 果
SMILE术前的等效球镜平均为(-5.68±0.34)D,术后等效球镜平均为(-0.23±0.18)D,SMILE-dif平均为(-5.48±0.28)D。Shammas、Haigis-L和Barrett True K公式计算的PE分别为(0.43±0.11)D、(0.51±0.28)D和(0.99±0.10)D(见图1)。在PE≤ 0.5D区间内Shammas、Haigis-L,Barrett True K公式分别占81%、79%、68%。
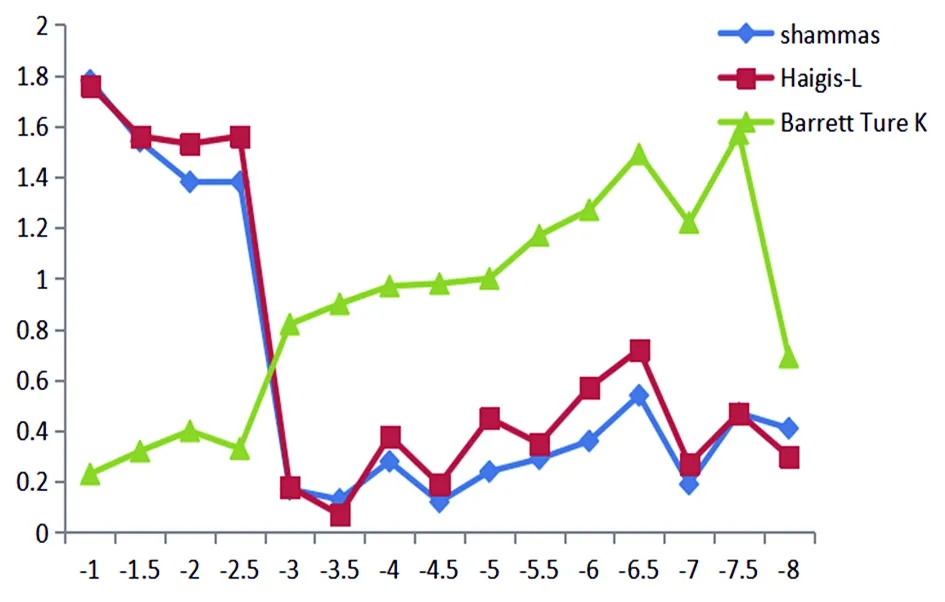
图1 不同SMILE术前等效球镜下,Shammas、Haigis-L和Barrett True K公式计算的PE值的变化规律
A组内Shammas、Haigis-L和Barrett True K公式计算的PE分别为(1.38±0.24)D、(1.55±0.02)D和(0.37±0.05)D,3组数据差异具有统计学意义(F=67.24,P< 0.05),说明在SMILE术前等效球镜在-3D以内Barrett True K公式较Shammas、Haigis-L更加精确。
B组内Shammas、Haigis-L和Barrett True K公式计算的PE分别为(0.27±0.15)D、(0.33±0.20)D和(1.09±0.26)D,3组数据差异具有统计学意义(F=57.09,P≤ 0.05)。其中Shammas和Haigis-L公式计算的PE没有统计学差异(P=0.46,>0.05),说明在SMILE术前等效球镜大于-3D时,Shammas和Haigis-L公式较Barrett True K公式准确。
讨 论
近视激光术后白内障人工晶状体度数计算是目前白内障手术医生面临的一个重要的困难[2,3]。研究发现近视激光术后白内障手术屈光误差向正的方向漂移,术后呈远视结果[4,5]。 近视激光术后人工晶体度数的计算误差主要有两方面的原因:角膜屈光力的测量误差与有效人工晶状体位置(effective lens position,ELP)计算误差(使用激光术后角膜参数引起的)[6]。几年来大约有20多种公式被用来计算近视激光术后人工晶状体度数[7]。其中主要分为两类:一类是需要近视激光手术术前资料的公式,另一类是不需要近视激光手术术前资料的公式。 本研究利用一个假想的白内障人工晶状体植入模型,假设给SMILE术后患者植入一个与SMILE术前相同度数的人工晶状体。认为SMILE手术引起的等效球镜变化应该与植入相同度数人工晶体引起的等效球镜的变化是相同的[8]。
本研究计算公式选用ARCS人工晶状体在线计算公式[9,10]中的Shammas、Haigis-L和Barrett True K对近视SMILE术后人工晶状体度数进行计算。这3个公式都是不需要术前资料的计算公式。Shammas、Haigis-L和Barrett True K公式研究证实在LASIK术后人工晶状体计算中较为精确[11,12]Barrett True-K公式是基于回归的公式,在有效晶状体位置的计算上采用了Barrett Universal II 和 Double-K 的计算方法[13]。Haigis-L公式通过在模型中加入一个矫正因子来优化ELP,该公式具有源于多元回归3个(a0、a1、a2)常数,即ELP=a0+a1×AC+a2×AL,AC为前房深度,AL为眼轴长度,a0、a1、a2由人工晶状体厂家提供[14]。Shammas 公式应用回归分析,通过优化LASIK术后的测量角膜K值来进行人工晶状体度数计算,即优化的角膜K值=1.14×术后LASIK K值[15]。
Wang等[10]研究认为ARCS屈光术后人工晶状体在线计算公式公式具有较小的IOL预测屈光误差,预测误差在0.5D范围内的患者占大多数。本研究结果跟Wang等[10]研究结果相似,其中Shammas、Haigis-L和Barrett True K公式计算的PE分别为(0.43±0.11)D、(0.51±0.28)D和(0.99±0.10)D。在PE≤ 0.5 D区间内Shammas、Haigis-L,Barrett True K公式分别占81%、79%、68%。3个公式在SMILE术后和LASIK术后人工晶状体度数计算中都能取得较好的结果。
在SMILE术前等效球镜度数小于-3 D时,Shammas、Haigis-L和Barrett True K公式计算的PE分别为(1.38±0.24)D、(1.55±0.02)D和(0.37±0.05)D,3组数据差异具有统计学意义,说明在SMILE术前等效球镜在-3 D以内Barrett True K公式较Shammas、Haigis-L更加精确。
在SMILE术前等效球镜度数大于-3 D时Shammas、Haigis-L和Barrett True K公式计算的PE分别为(0.27±0.15)D、(0.33±0.20)D和(1.09±0.26)D,3组数据差异具有统计学意义。其中Shammas和Haigis-L公式计算的PE没有统计学差异,说明在SMILE术前等效球镜大于-3 D时,Shammas和Haigis-L公式较Barrett True K公式准确。
总之,本研究认为在SMILE术前等效球镜度数小于-3 D时选用Barrett True K公式,在SMILE术前等效球镜大于-3 D时选用Shammas和Haigis-L公式较为准确。
