M型袋口折边复原机构设计与运动学分析

陶 闱，陆佳平，王婧月

（江南大学 机械工程学院，江苏无锡 214122）

0 引言

M型折边包装袋是目前市面上使用最为广泛的包装形式之一，具有袋式新颖、节约空间和尺寸规格灵活等优点[1]。其在充填完成后呈现自由开放袋口，需对折边进行复原后再封口。目前折边复原大多采用人工，劳动强度大，工作效率低；少部分采用机械结构，即通过单一侧边插片或击打杆辅助袋口按预折线进行折叠，结构简单，但对包装袋本身的挺度要求较高，且包装袋封口处有较多留边，材料浪费严重[2-4]。因此设计一款新型的M型袋口折边复原机构，具有十分重要的现实意义。

本文设计一款组合连杆式M型袋口折边复原机构，在折边的同时，利用撑袋装置确保包装袋袋口不变形，以提高折边机的包装适应性及折边成功率。但由于连杆自身特性及惯性力等原因，运动过程中，易产生较大的机械振动和冲击[5]。因此，有必要对机构的结构参数进行优化。本文以M型袋口折边复原机构为研究对象，首先基于闭环矢量方程构建机构的运动学模型[6-7]，分析摆杆末端的运动表达式，并分别运用MATLAB和SolidWorks对机构进行数值计算和虚拟仿真[8-9]，以验证运动学模型的正确性及机构设计的合理性；然后，以旋转点角加速度最小为目标构建优化函数，并利用MATLAB优化工具箱进行求解[10-12]，以提高机构运动的稳定性，为后续动力学分析提供理论依据。

1 折边复原机构技术方案

1.1 机构工艺方法

根据研究分析，M型袋折边复原机构需满足以下设计要求：

（1）适应不同材料的包装袋的折边需求，且结构简单，动作灵活。

（2）机构与包装袋之间是柔性接触，不能有尖端存在而戳破包装袋。

（3）确保包装袋沿预折线完成折边，且折边过程中不会发生变形而导致折边错位、皱折等现象。

（4）机构生产效率与整个包装生产线的生产能力配合，且在生产线中的布局不影响后序工位的运作。

鉴于上述设计要求，确定M型袋折边复原机构动作过程：（1）机构插入袋口，准备折边；（2）折边装置摆动使包装袋按预折线折叠，同时撑袋装置固定包装袋四角，确保包装袋在折边过程中不会发生变形。图1为折边动作示意图。

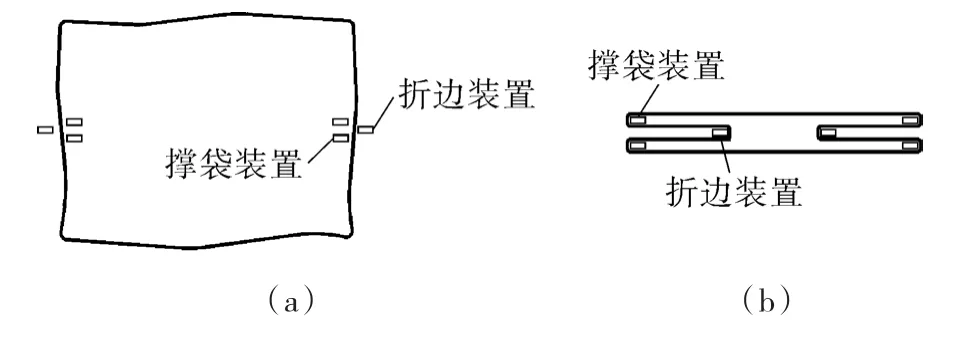
图1 折边动作过程示意图Fig.1 Schematic diagram of folding action process

1.2 机构工作原理

M型袋口折边复原机构主要由撑袋装置和折边装置2部分组成，两者通过工字杆联动，并通过气缸驱动完成折边复原动作。其动作的完成率直接关系包装袋的封口质量及整个包装机的工作效率。图2为M型袋口折边复原机构的虚拟模型，其中A、B、C、D为固定铰链。

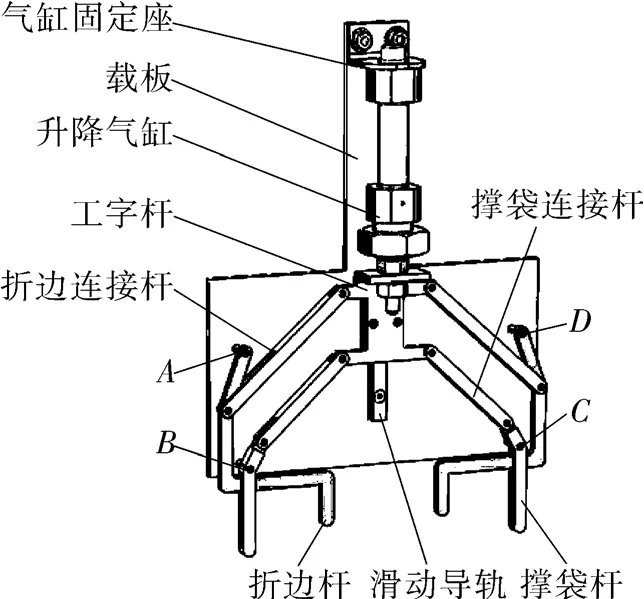
图2 折边复原机构模型Fig.2 Model of M-shaped bag mouth folding restoring mechanism

初始时，折边杆和撑袋杆均处于打开状态，当包装袋完成充填，由升降气缸带动工字杆沿着滑动导轨做直线运动，同时通过折边连接杆和撑袋连接杆带动折边杆、撑袋杆闭合，完成折边复原。其中撑袋杆上设置有U形长槽，当折边杆闭合时，插入U形长槽中，以确保最佳的折边复原效果。

2 机构运动学仿真分析

为验证机构设计的合理性，分别对撑袋装置和折边装置进行运动学分析。

2.1 撑袋装置

为便于分析计算将撑袋装置简化成如图3所示。以机架G点为原点建立相应的直角坐标系。其中，Ly表示A点到G点的垂直距离；Lx表示A点到G点的水平距离。

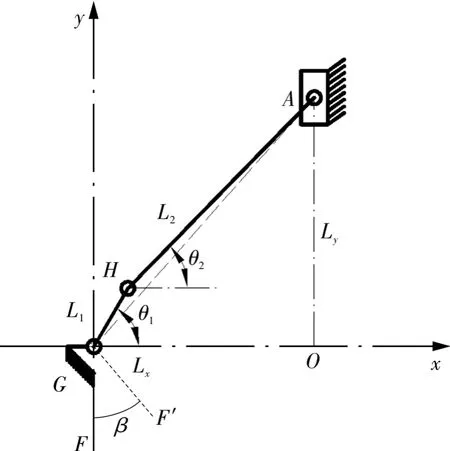
图3 撑袋装置运动简图Fig.3 Schematic motion diagram of bag stretching device

杆L1-L2-Ly-Lx构成矢量多边形，矢量之和等于 0，即：

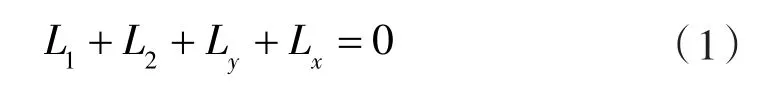
矢量多边形L1-L2-Ly-Lx在x轴、y轴上的投影满足方程：

由装配关系可知：

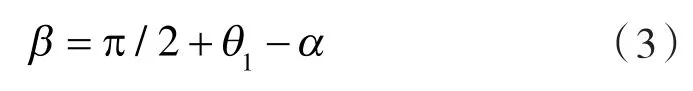
其中，α为∠FGH。

分析摆杆GF末端F点位移、速度及加速度的变化规律。

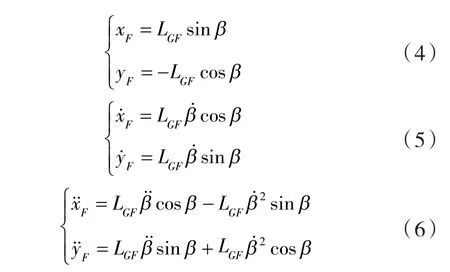
在保证机构满足正常运作的条件下，取撑袋装置的设计参数：L1=16 mm，L2=40 mm，Lx=32.5 mm，Ly=37 mm，α=150°。整个运动循环时间为3 s，其运动流程：工字杆在气缸驱动下向上运动16 mm，使撑袋杆闭合，运动时间为0.5 s，为便于折边袋塑性形成弹性记忆，此过程持续1.5 s；然后工字杆复原，至此完成1个循环。

分别利用MATLAB和SolidWorks进行数值计算和虚拟仿真，得到摆杆末端F点位移、速度和加速度曲线，如图4所示。两者曲线基本吻合，数值大小相近，误差较小，运动学模型正确，机构设计合理。

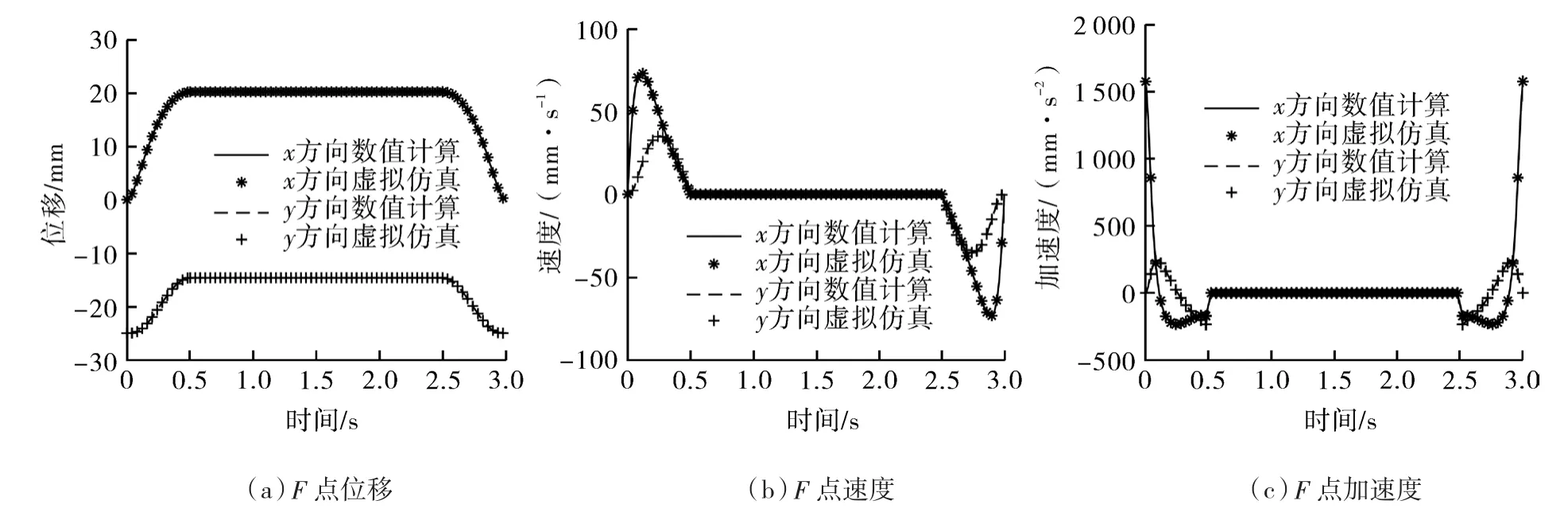
图4 F点对比曲线Fig.4 F correlation curve

2.2 折边装置

将折边装置结构进行简化，如图5所示。以机架A点为原点建立对应的直角坐标系。其中，Ly表示B点到A点的垂直距离，Lx表示B点到A点的水平距离。

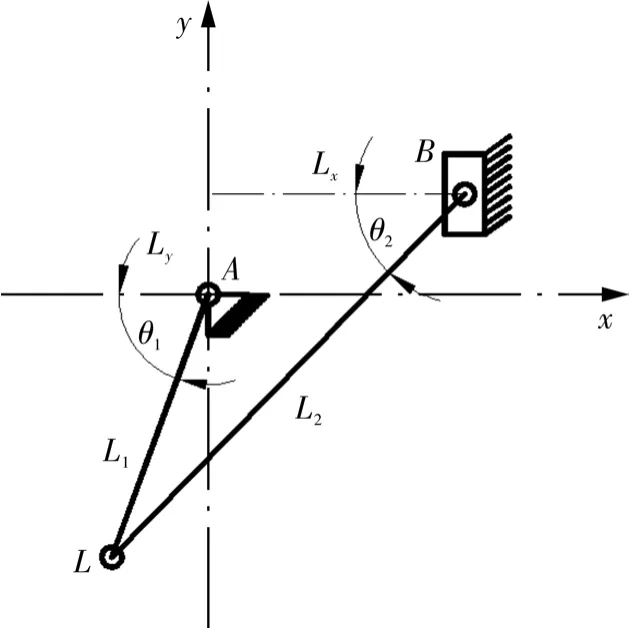
图5 折边装置运动简图Fig.5 Schematic motion diagram of folding device

杆L1-L2-Ly-Lx构成矢量多边形，矢量之和等于 0，即：

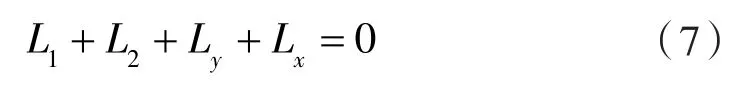
矢量多边形L1-L2-Ly-Lx在x轴、y轴上的投影满足方程：

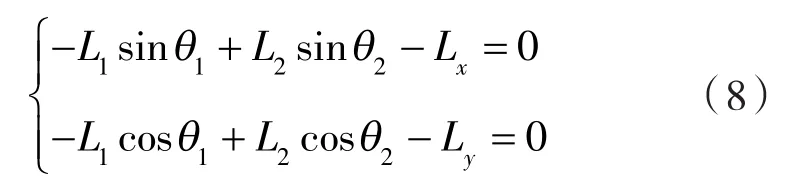
已知折边杆为异型杆，其末端的运动规律随着L点的变化而变化，故对摆杆AL末端L点位移、速度及加速度进行分析：

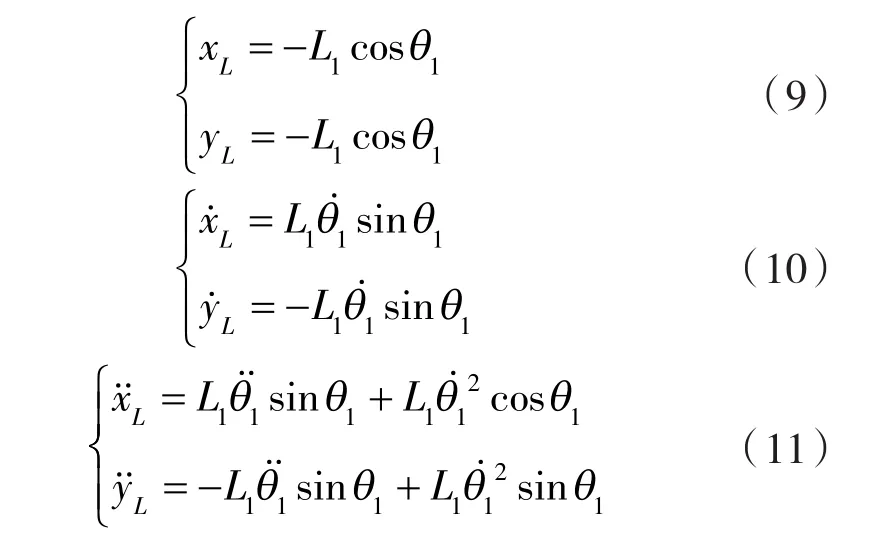
设置折边装置的设计参数：L1=28 mm，L2=50 mm，Lx=25 mm，Ly=10 mm。

同上，运用MATLAB和SolidWorks对装置分别进行数值计算和虚拟仿真分析，得到图6。分析可知，曲线基本吻合，误差较小，运动学模型的正确性和机构的合理性得以验证。

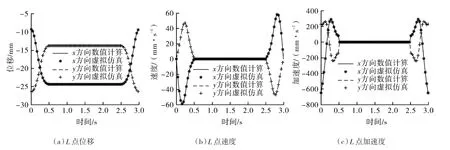
图6 L点对比曲线Fig.6 L correlation curve

3 运动学优化设计

为减少装置机械振动及杆末端与包装袋接触时的冲击力，分别对撑袋装置及折边装置结构参数进行优化。

3.1 撑袋装置

3.2 折边装置

折边杆由4段固定构成，除L1外其他部分的尺寸与折边袋的尺寸和实际工况有关，不随L1的变化而变化，且与L点固定连接。为减少末端加速度，即可认为减小A点角加速度，故取A点角加速度最小为目标函数，即：

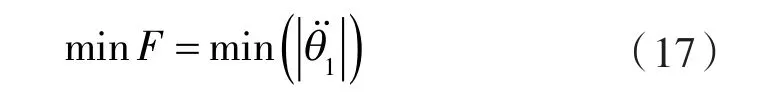
minF 是 L1、L2、Lx、Ly的函数，则将设计变量表示：

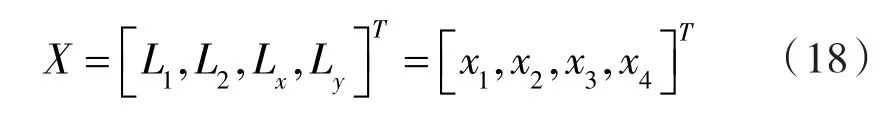
受滑块行程的限制，此机构无需考虑死点位置的存在。

综合考虑运动规律及机构布局要求，对机构尺寸做如下式所示限定：

3.3 优化求解

对于多维约束非线性优化问题，可采用MATLAB非线性约束优化函数fmincon求解。函数的数学模型：

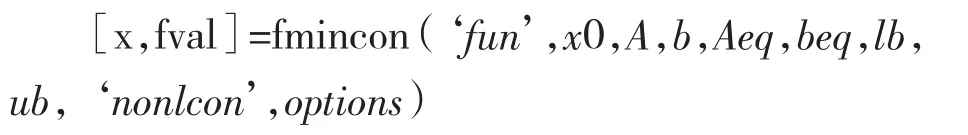
式中：

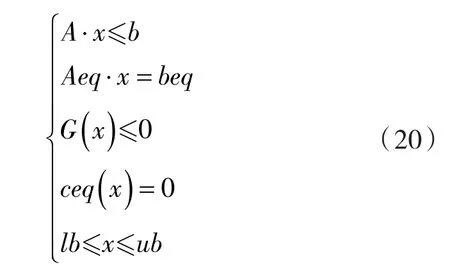
经计算优化后的撑袋装置各杆长：L1=12 mm，L2=45.49 mm，Lx=38 mm，Ly=37 mm。折边装置各杆长：L1=26.58 mm，L2=49.56 mm，Lx=27.34 mm，Ly=10.17 mm。

4 优化结果分析

4.1 撑袋装置

图7（a）、（b）、（c）分别为撑袋装置在G 点角加速度、F点x方向加速度和F点y方向加速度优化曲线。分析可知，优化后撑袋装置加速度较优化前有较大的减少。优化前G点初始角速度为62.96 rad/s2，优化后为21.05 rad/s2，减少了41.91 rad/s2。优化前F点x方向初始加速度为1 545.86 mm/s2，优化后为526.12 mm/s2，减少了1 019.74 mm/s2。优化前F点y方向初始加速度为241.23 mm/s2，优 化后为 80.05 mm/s2，减少了 161.18 mm/s2。

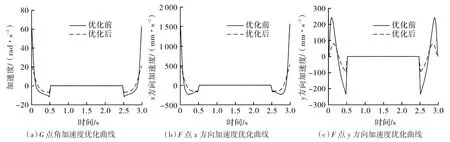
图7 撑袋装置优化前后对比Fig.7 Comparison before and after optimization of bag stretching device

4.2 折边装置

图8（a）、（b）、（c）分别为A点角加速度、L点x方向加速度和L点y方向加速度对比曲线。从图中可看出，优化前A点初始角加速度为24.62 rad/s2，优化后为 21.78 rad/s2，减少了 2.84 rad/s2。优化前L点x方向初始加速度为650.61 mm/s2，优化后为589.1 mm/s2，减少了61.51 mm/s2。优化前L点y方向初始加速度为227.68 mm/s2，优化后为158.05 mm/s2，减少了 69.63 mm/s2。

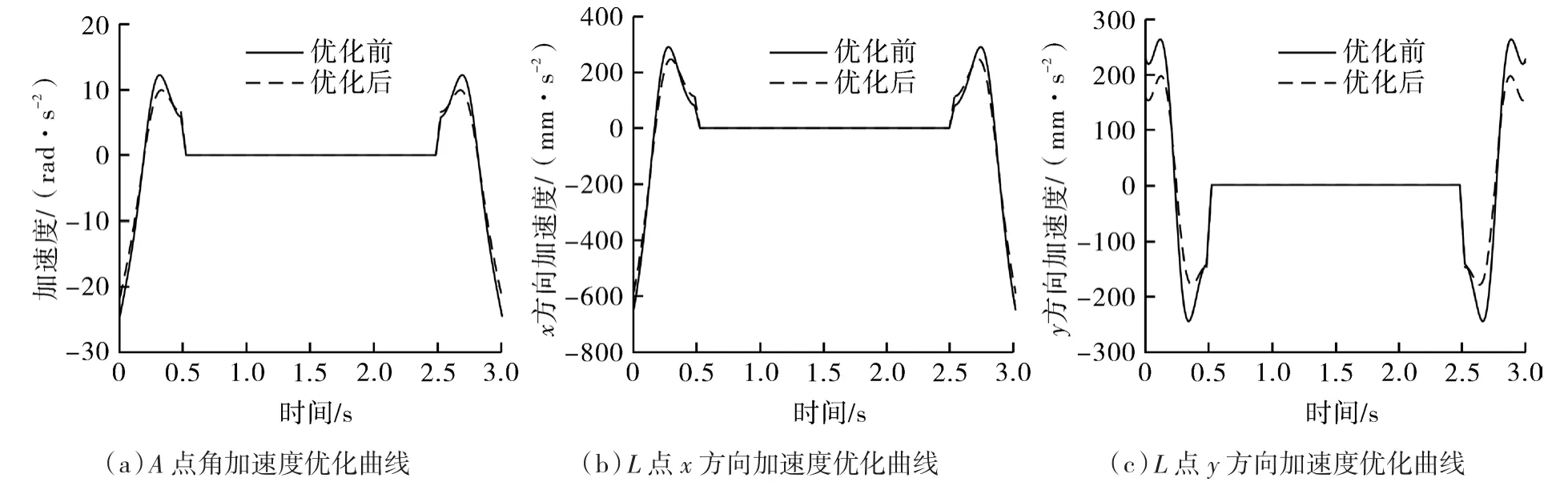
图8 折边优化前后对比Fig.8 Comparison before and after edge folding optimization

5 结语

（1）以M型袋口折边复原机构为研究对象，根据机构运动特点，将2个主要机构简化为2个偏置曲柄滑块机构；利用闭环矢量方程法构建相应的数学模型，并得到摆杆末端的位移、速度和加速度的解析式。建立机构虚拟样机，对比数值计算和仿真分析结果，验证数学模型和机构运动的合理性。

（2）为减少机构运动过程中的机械振动和末端冲击力，以摆杆旋转点角加速度为目标函数，综合机构整体布局、结构形状和机构联动等因素合理限定约束条件，对机构进行运动学优化设计，对比优化前后的旋转点角加速度和摆杆末端加速度。优化后的撑袋装置G点角加速度降低了66.57%，折边装置A点角加速度降低了11.54%，优化效果显著，减少对整机的冲击振动及磨损，延长气缸和折边装置的寿命。相关研究数据为后续动力学分析与研究提供理论依据。