三维均匀磁场主动补偿系统及其特性研究

金 铭,刘金生,Akiti Kenneth Tetteh, Nwodom Tochukwu Eric-Theophilus,李曙光

(浙江科技学院 自动化与电气工程学院,杭州 310023)

零磁空间就是理论上磁场为绝对零值的磁场环境。受技术条件限制,目前采用人工手段尚难以实现绝对的零磁空间,只能实现极弱的近零磁场环境[1]。在基础物理领域,在零磁空间内能对常用铁磁零部件进行缺陷检测[2]。在生物物理领域,零磁空间可用于探讨外界所加磁场对生物体的基因表达、生长发育、行为习惯等造成不同程度的干预[3]。在医学领域,零磁空间能屏蔽生物体外磁场,从而检测出生物体内微弱的磁场信号[4]。在地球物理领域,通常利用零磁空间确定岩石剩余磁场以此判断岩石磁化历史,为古磁场特征的描述作铺垫[5]。因此,零磁空间是磁领域科学研究发展的重要基础[6]。

磁场屏蔽通常采用被动屏蔽和主动补偿2种方法[7]。被动屏蔽即钢板屏蔽[8],例如德国国家物理技术研究院(Physikalisch-Technische Bundesanstalt,PTB)的零磁实验室[9]、日本超导实验室的“大波斯菊(COSMOS)”等将坡莫合金磁性层作为外壳从而屏蔽地磁场的方式即为被动屏蔽[10]。但相对于主动补偿而言,被动屏蔽需要对母体建筑空间、承重、周边环境等进行详细的评估和测试,需进行周密的设计和繁复的施工,因此该方法不仅工程量大,而且消耗成本高[11]。

相比被动屏蔽,主动补偿具有性能稳定、效果良好、造价低廉、安装方便,不需要进行大量设计工作且适用性强,使用灵活等优点[7]。郭勇志等研究发明了一种保证磁场传感器位于稳定磁场环境中并实现快速测量的三轴双向补偿式磁场测量装置[12];金贵等[13]在磁感应相位移技术检测脑出血的试验研究中提出一种对侧半球抵消(contralateral hemisphere cancellation,CHC)线圈,能够抵消主磁场及脑左右半球正常脑组织产生的感应磁场。何哲玺等[14]发明了用于微型核磁共振陀螺仪的磁补偿线圈结构件。Matti等[15]为实现在不受约束的对象上进行可穿戴式脑磁图记录,设计了一种三维方形线圈补偿屏蔽室内空间中不均匀的剩余磁场。以上研究虽均能达到补偿地磁场的目的,但环境扰动、传感器扫描速度对所研究系统的影响尚缺乏足够的研究。因此,我们设计并搭建了一个三维均匀磁场主动补偿系统,使其中心区域能够产生均匀磁场,本系统装置简单并能有效补偿地磁场。

1 试验原理与方法

磁补偿线圈常用骨架为圆柱形,圆柱形具有空间利用率高,使用灵活等优点。本研究采用2种圆柱形线圈来补偿地磁场,Lee-Whiting线圈[16]和cosθ线圈[17],它们分别能在轴向和径向上产生范围较大的均匀磁场。其中,Lee-Whiting线圈用来补偿Z轴方向磁场[18],cosθ线圈用来补偿XY轴方向磁场[19]。

1.1 Lee-Whiting线圈原理

Lee-Whiting线圈由4个相同、平行且共轴的圆线圈构成,通电后会在其Z轴周围一定区域内产生均匀的磁场。

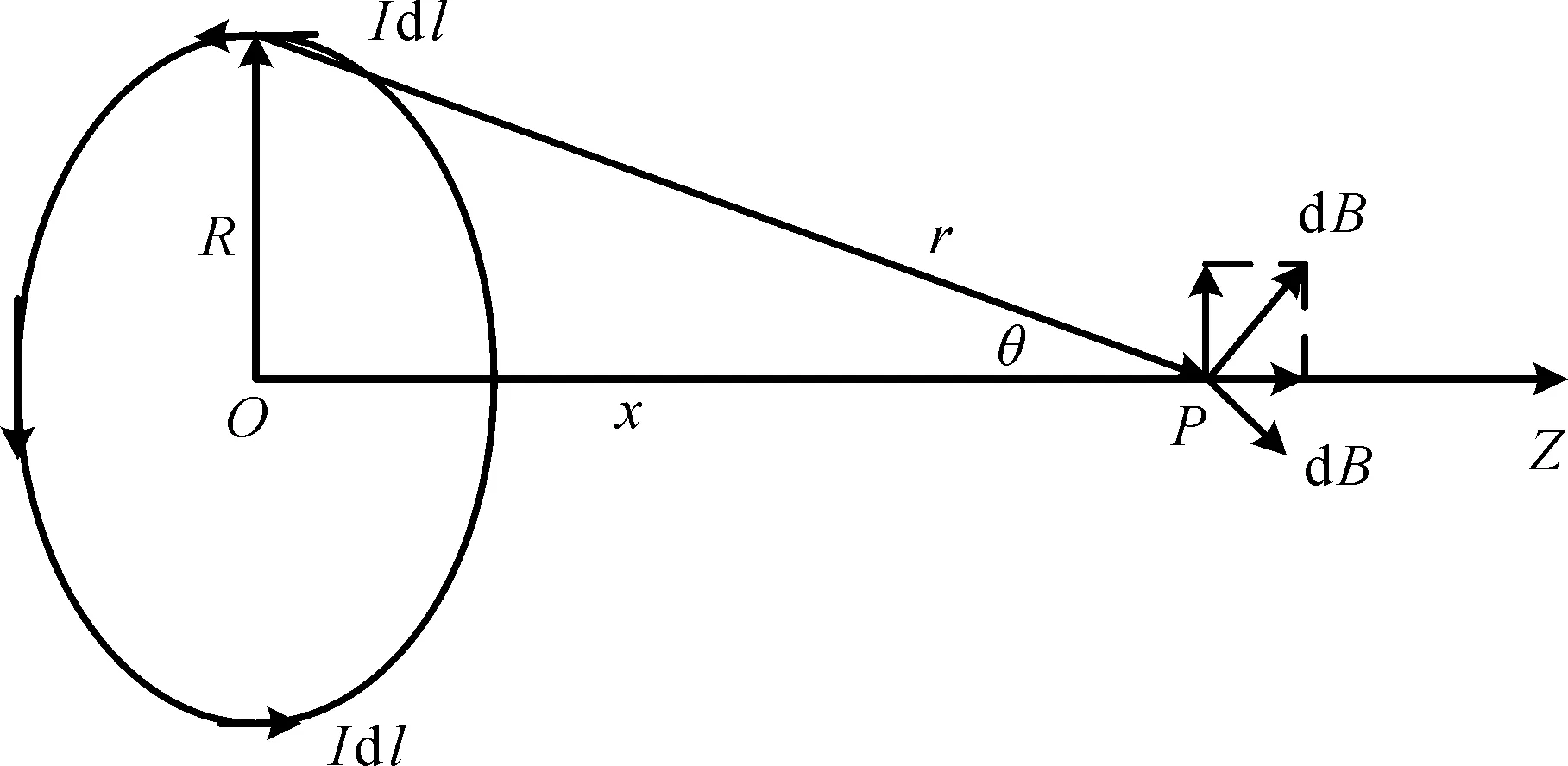
图1 通电圆线圈轴线上任一点的磁场作用示意图Fig.1 Schematic diagram of magnetic field action at any point on the axis of energized circular coil

图1为通电圆线圈轴线上任意一点的磁场作用示意图。根据毕奥萨伐尔定律(Bio-Savart Law),可推出通电圆环中心轴线上任一点磁场的大小为

(1)

式(1)中:B为轴线上任意一点P在圆线圈作用下受到的磁场;μ0为真空导磁率;N0为线圈匝数;I为圆线圈电流;R为圆环半径;x为中心轴线上一点到圆心的距离。

图2 Lee-Whiting线圈示意图Fig.2 Schematic diagram of Lee-Whiting coil

图2为Lee-Whiting线圈示意图。如图2所示,以轴线中心为原点,4个圆线圈互相串接。当电流为I时,若点P位于轴线上,则4个圆线圈产生的磁场方向一致,根据式(1),可得到每个圆线圈作用于点P的磁场大小,如式(2)所示,利用磁场叠加定理,可计算出轴线上任一点磁场强度。

(2)

式(2)中:BA、BB、BC、BD分别为4个通电圆线圈作用于点P的磁场大小;d1、d2分别为OA、OB及OC、OD与点O间的距离。

当点P为轴外一点时,需建立圆柱坐标系计算磁感应强度。以圆柱坐标系空间中任意一点P(r1,θ1,z1)为例,在r-θ平面上有一个半径为a的圆形通电线圈,其中心位于原点处,可计算得到点P处由电流I产生的磁场矢势A。通过计算旋度(A)可以得到磁场径向分量和轴向分量,其计算公式[16]为

(3)

(4)

式(3)～(4)中:Br为径向磁场大小;Bz为Z轴方向磁场大小;r1为待求点距离中心轴线的距离;z1为Z轴坐标;K为第一类完全椭圆积分;E为第二类完全椭圆积分。

由于圆柱坐标的对称性,第三分量Bθ被抵消后为零,且径向与轴向磁场分量互相垂直,因此最终轴外一点的磁场

(5)

利用式(1)～(5),可计算出Lee-Whiting线圈空间内任意一点的磁场大小,并由此得到线圈空间中任意一点磁场大小相对于线圈中心点磁场大小的误差公式为

(6)

式(6)中:e为磁补偿系统空间中任意一点磁场大小相对于其中心点磁场大小的相对误差;B0为装置中心点磁场大小;BP为空间中任意一点的磁场大小。

1.2 cosθ线圈原理

图3 cosθ线圈模型Fig.3 Model of cosθ coil

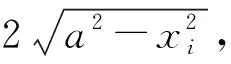
图3中P为空间任意一点,L1、L2、L3、L4分别为4根对称载流导线,以这4根载流导线为一组,其他几组以此类推,依据载流导线外一点的磁场公式[20]可计算出每根载流导线对空间中任意一点P的总磁场B。每根载流导线对该点产生的总磁场可分解到垂直和水平方向。载流导线L1、L2、L3、L4在水平方向的磁场分量如下:

(7)

式(7)中:B1、B2、B3、B4分别为载流导线L1、L2、L3、L4在水平方向的磁场分量;θh1～θh4为每根载流导线对点P产生的总磁场方向与X轴的夹角;x、y分别为空间中任意一点P的X、Y轴坐标。

载流导线L1、L2、L3、L4在垂直方向的磁场分量如下:

(8)

式(8)中:B5、B6、B7、B8分别为载流导线L1、L2、L3、L4在垂直方向的磁场分量;θv1～θv4为每根载流导线对点P产生的总磁场方向与Y轴的夹角。

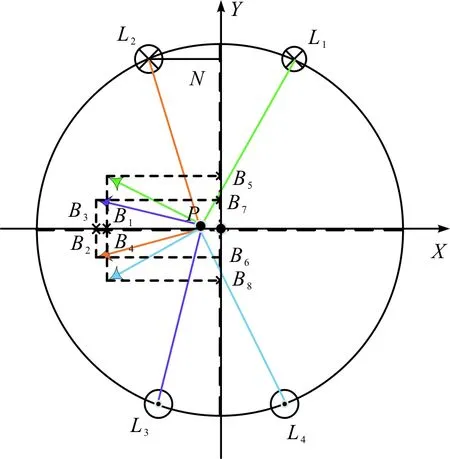
图4 载流导线L1、L2、L3、L4作用于 点P时的磁场分解图Fig.4 Decomposition diagram of magnetic field when current-carrying wires L1、L2、L3、L4 act on point P

图4为载流导线L1、L2、L3、L4作用于点P时的磁场分解图。将每根载流导线在点P产生的总磁场分解到垂直与水平方向,再根据水平和垂直方向上的磁场分量求出作用于点P的磁场大小,其计算过程如下:

(9)

式(9)中:Bh为总磁场的水平分量;Bv为总磁场的垂直分量;B为cosθ线圈空间中任一点受到所有载流导线的总磁场大小。

1.3 三轴磁场传感器特性曲线

试验采用HMC5883L三轴磁场传感器来测量磁补偿系统的磁场,以100 Hz频率对数据进行采样。为提高测量数据结果的可靠性,通常利用亥姆霍兹线圈来绘制三轴磁场传感器特性曲线。制作一个直径为7.5 cm,每个绕组匝数为10的亥姆霍兹线圈,计算不同电流下亥姆霍兹线圈中心点理论磁场值,其中心点磁场理论曲线方程为B=238I。其中,B为中心点理论磁场;I为电流,电流范围为0～1.8 A,步长为0.05 A。

为排除地磁场干扰,将亥姆霍兹线圈置于一个剩余磁场小于1 nT的磁屏蔽筒内,并将磁场传感器置于亥姆霍兹线圈中心位置,分别测试磁场传感器在X、Y、Z轴3个方向上随电流增加而变化的磁场。为提高特性曲线在较大磁场范围内的通用性,测试范围应尽可能广。电流以0.05 A为步长从0 A增加到1.8 A,记录不同电流下产生的磁场数据并绘图。图5为三轴磁场传感器的特性曲线,其中图5(a)为X方向,图5(b)为Y方向,图5(c)为Z方向。由图5可知,在3个方向上测试得到的3条特性曲线趋势相同,均随电流的增加,磁场增加趋势变缓。

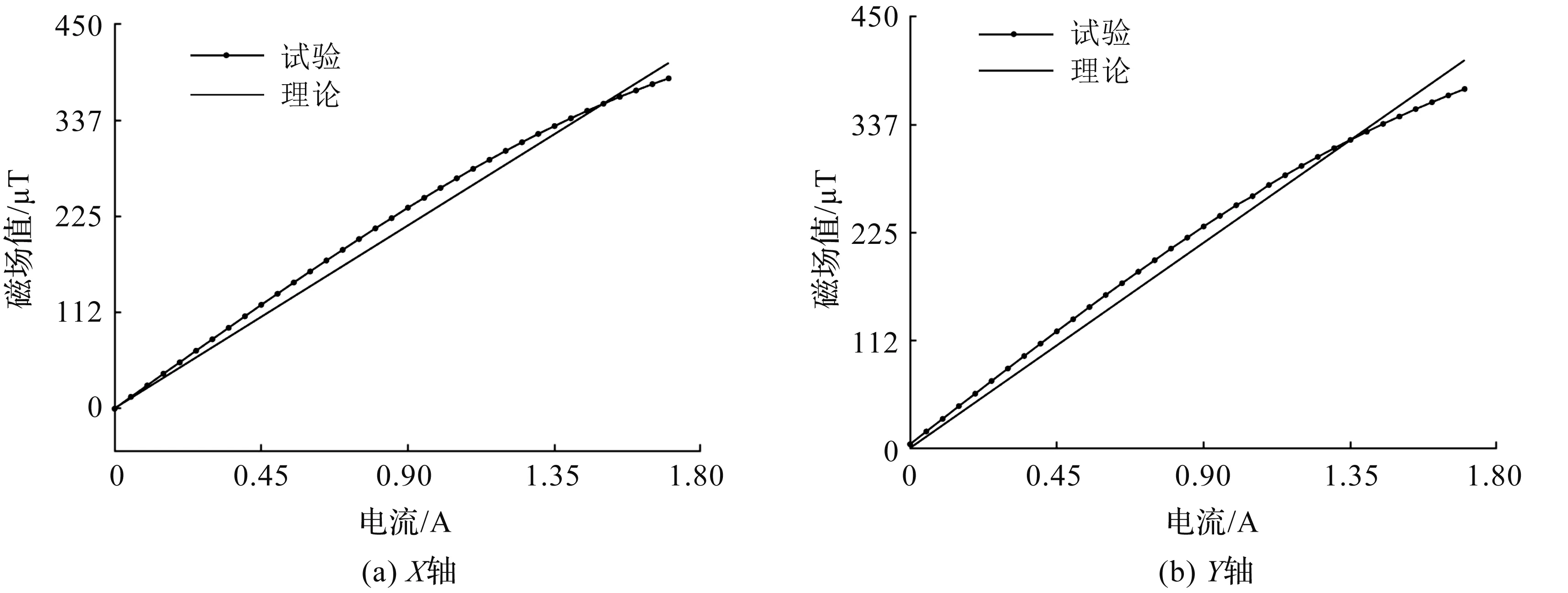
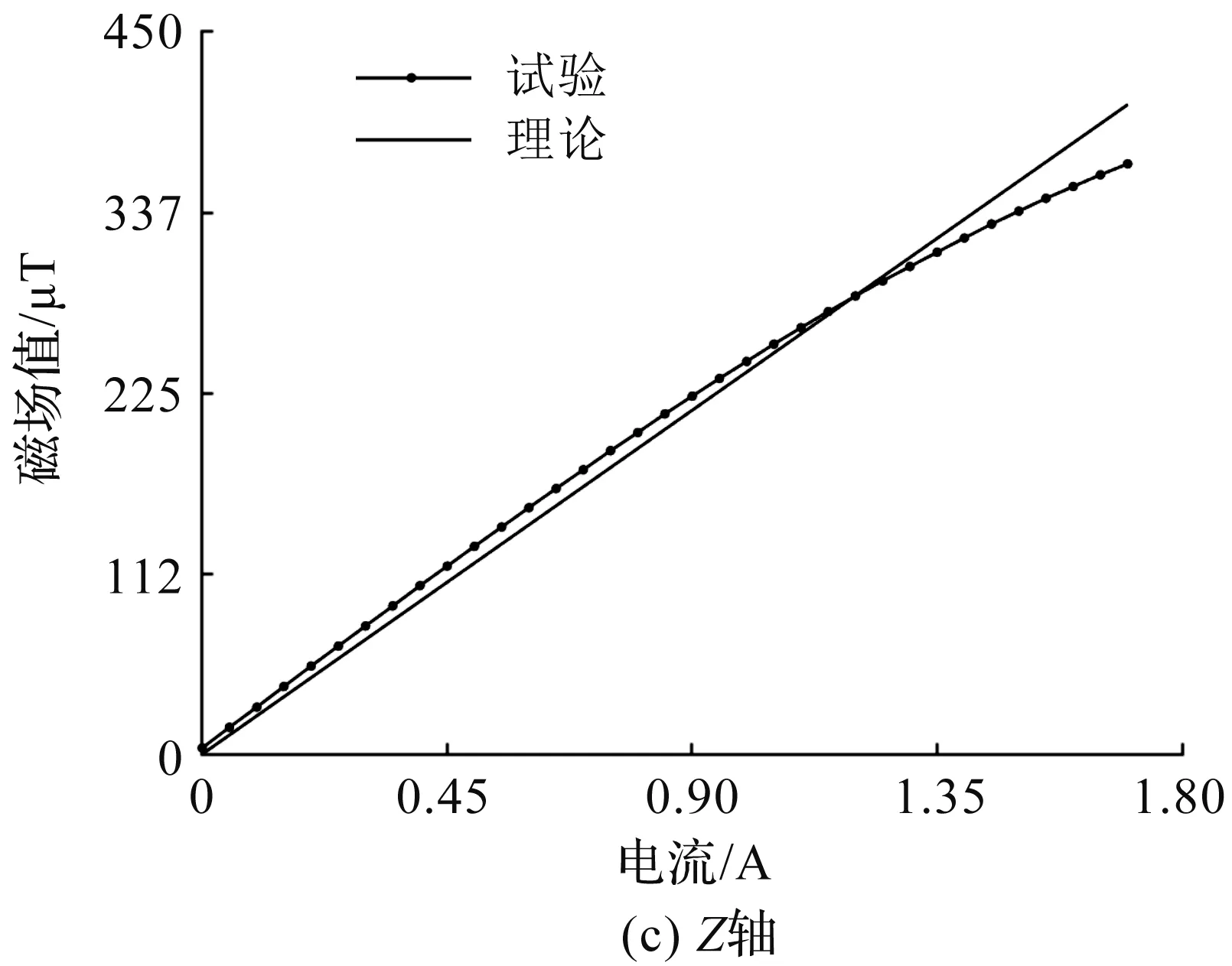
图5 三轴磁场传感器的特性曲线Fig.5 Characteristic curve of triaxial magnetic field sensor

2 试验装置参数及制作

三维均匀磁场主动补偿系统的硬件部分由三维补偿线圈、多路直流恒流可调电源、HMC5883L磁场传感器和运动控制平台组成。

三维补偿线圈由1个Lee-Whiting线圈、2个cosθ线圈组成,均采用无磁材料制作。Lee-Whiting线圈由4个相同的平行且共轴的圆形线圈串接而成,直径均为d=18 cm,用0.55 mm的漆包线进行绕制,其匝数从左到右分别为81、36、36、81,其圆心与轴线中心点的距离从左到右依次为0.470 4d、0.121 6d、0.121 6d、0.470 4d,并用M4的螺杆将其固定。2个cosθ线圈的圆柱骨架分别为长25 cm、直径11 cm和长30 cm、直径7.5 cm。用0.55 mm的漆包线分别在2个骨架上串接矩形回路构成cosθ线圈,其中直径较大的线圈矩形回路数为16,每个矩形回路匝数为11,整个线圈匝数为176;直径较小的线圈矩形回路数为6,每个矩形回路匝数为7,整个线圈匝数为84。

运动控制平台由3个型号为57HB56L4的步进电机组成,能够实现磁场传感器在X、Y、Z轴3个方向上的运动。采用型号为3DM2250M的三相步进电机控制器,其输出电压为48 V,最高分辨率可达每转60 000个脉冲,最高响应频率为200 kHz,内部采用伺服控制原理电路,使得电机能够稳定运行。利用实验室虚拟仪器工程平台(Laboratory Virtual Instrument Engineering Workbench,LabVIEW)开发程序,通过美国国家仪器有限公司(National Instruments,NI)的USB-6009多功能卡产生精确控制的数字脉冲信号,然后通过控制器使磁场传感器按程序设定好的路线扫描空间内的磁场。

将绕制好的3个线圈进行嵌合,使3个线圈中心点重合且轴线方向两两正交。图6为三维均匀磁场主动补偿系统。因地磁场属于直流磁场,比较稳定,因此将Lee-Whiting线圈和cosθ线圈通以一定的直流电流,使其分别在Z轴和X、Y轴方向上的中心区域产生均匀的恒定磁场来补偿地磁场。

图6 三维均匀磁场主动补偿系统Fig.6 An active compensation system for three-dimensional uniform magnetic field

3 分析与讨论

3.1 环境扰动对磁场波动与测试准确性的影响

本试验主要研究由环境噪声引起的环境扰动对磁补偿系统内部磁场波动及测试结果准确性的影响,因此,测试中将环境噪声设置为唯一变量,第一次试验在环境噪声约为46 dB条件下进行。利用磁场传感器测试磁补偿系统中心点位置磁场,共获得400组数据,并观察磁场波动情况及测试准确性。图7是噪声约为46 dB时系统中心点磁场数据直方图统计及其高斯拟合结果。在统计学中,通常用标准差σ作为统计分布的测量依据,它能反映数据离散程度。而高斯拟合中半高宽(full width at half maximum,FHWM)约为2.355σ,因此FWHM也能反映数据离散程度;峰位表示出现频率最高的数值,能反映测量数据的准确性。根据图7中的高斯拟合结果绘制表格,见表1。

图7 噪声约为46 dB时系统中心点磁场数据直方图统计及其高斯拟合结果Fig.7 Histogram statistics of magnetic field data at center of the system and their Gaussian fitting results with noise being about 46 dB

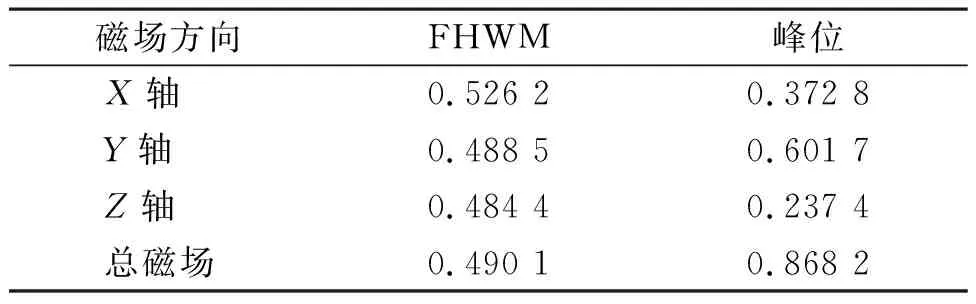
表1 噪声约为46 dB时X、Y、Z轴3个方向磁场及 总磁场数据的高斯拟合结果Table 1 Gaussian fitting results of magnetic field data in X, Y and Z directions and total magnetic field data with noise being about 46 dB μT

第二次试验在环境噪声约为17 dB的条件下进行,其中,传感器及磁补偿系统中心点位置与第一次试验中的一致。图8是噪声约为17 dB时系统中心点磁场数据直方图统计及其高斯拟合结果。根据图8中的高斯拟合结果绘制表格(表2),由表可知,环境噪声为17 dB时参数FHWM与峰位均比环境噪声为46 dB时的更低,说明对于测量空间中同一点的磁场值,当环境噪声为17 dB时测量结果更加稳定且被补偿后的地磁场更接近“零”磁。可见,由噪声引起的环境扰动对磁场数据的影响较大,在相对安静的环境中装置内磁场数据平稳,更利于补偿地磁场。这说明环境噪声是影响装置内磁场波动及试验测量结果准确性的一个重要因素,故后续试验将在环境噪声约为17 dB的环境中进行。

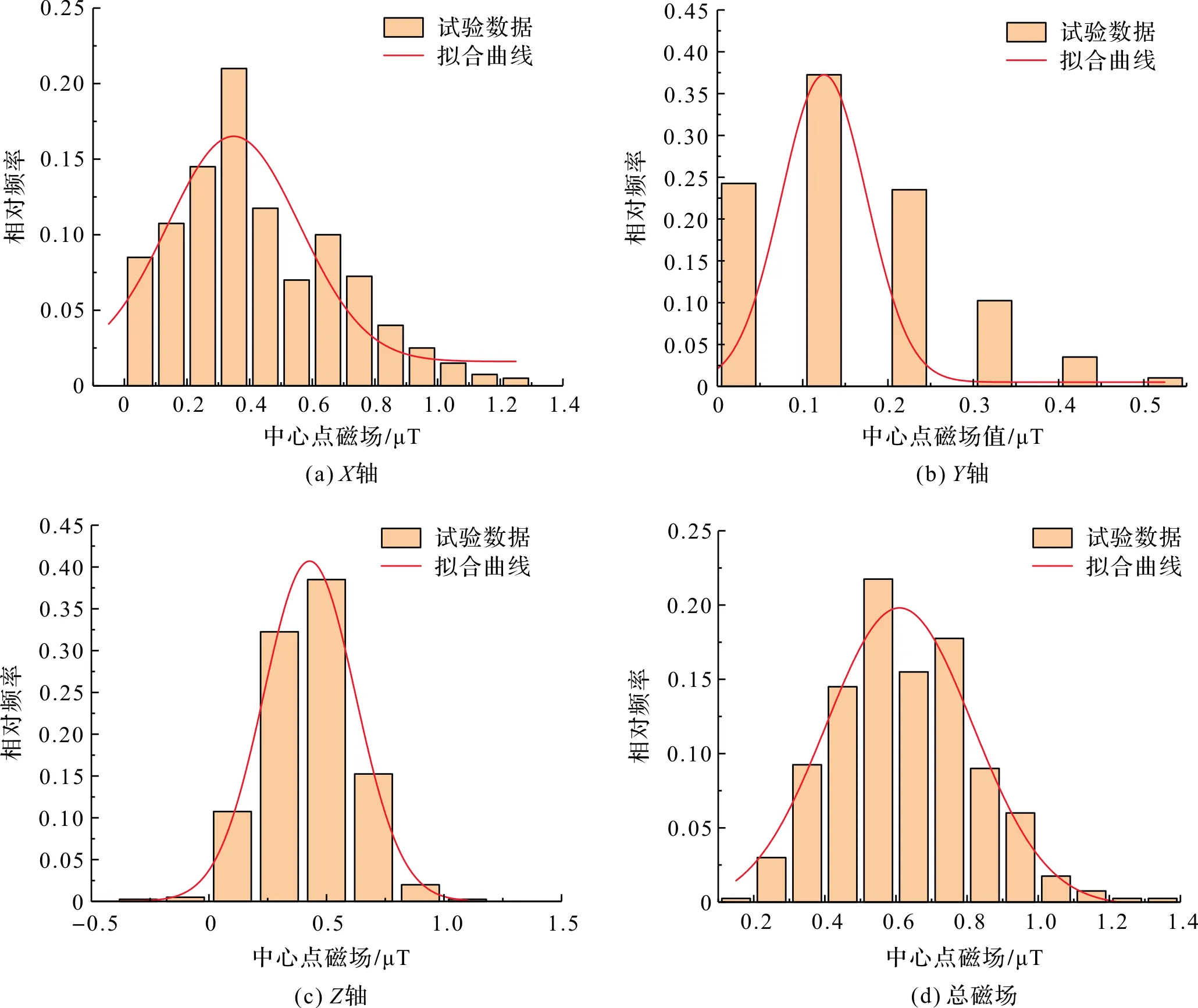
图8 噪声约为17 dB时系统中心点磁场数据直方图统计及其高斯拟合结果Fig.8 Histogram statistics of magnetic field data at center of the system and their Gaussian fitting results with noise being about 17 dB

表2 噪声约为17 dB时X,Y,Z三个方向磁场及总磁场数据的高斯拟合结果Table 2 Gaussian fitting results of magnetic field data in X, Y and Z directions and total magnetic field data with noise being about 17 dB μT

3.2 传感器扫描速度对磁场的影响

为减少环境噪声对磁场测试的干扰,本试验将在环境噪声约为17 dB的环境中进行。通过调节3个方向的电流,将本磁补偿系统中心所加磁场设置为63.27 μT,而后在其他试验条件不变的情况下,改变磁场传感器的扫描速度,使其分别为4.5、9.0、13.5 mm/s。图9为不同扫描速度下磁补偿系统中心轴线上的磁场测试结果。

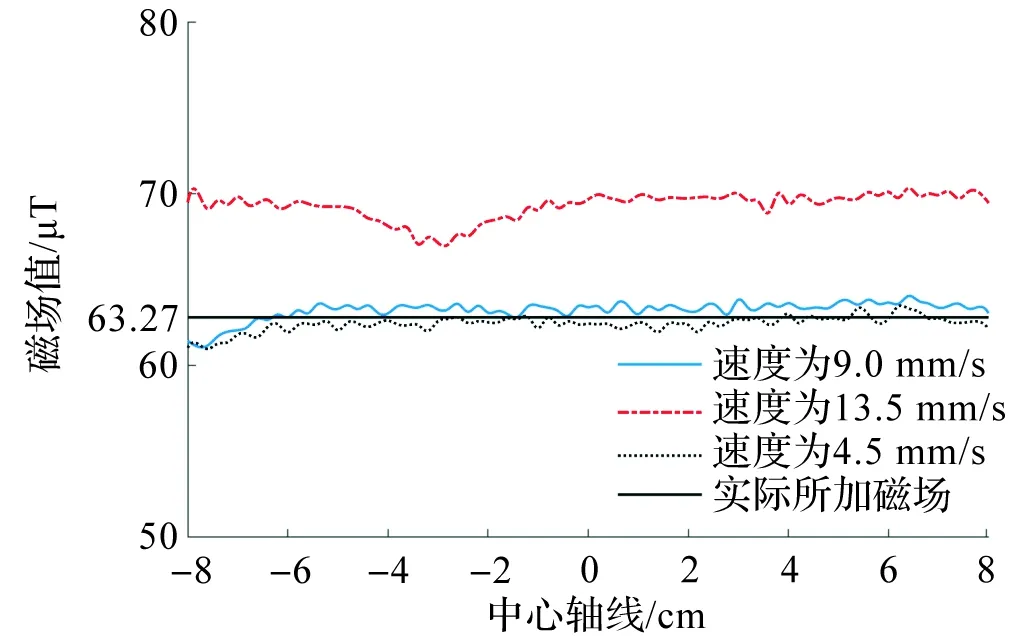
图9 不同扫描速度下磁补偿系统中心轴线上的磁场测试结果Fig.9 Magnetic field test results on the central axis of the magnetic compensation system at different scanning speeds

由图9可知,当扫描速度为13.5 mm/s时,磁场数据明显偏离实际所加磁场,且当扫描位置处于中心轴线-3 cm左右处时磁场数据最小,对比扫描速度为9.0 mm/s与4.5 mm/s时,磁场数据在中心轴线上-8 cm处时已经处于最小值,而后逐渐增加并趋于稳定。由此说明当磁场传感器扫描速度过快时,会影响磁场传感器的读取数据速度,使其无法及时追随其扫描速度,由此产生数据滞后现象,导致试验产生系统误差,影响试验结果;当磁场传感器扫描速度为4.5 mm/s或9.0 mm/s时二者的试验测试曲线总体趋势相近,且均接近实际所加磁场,但当扫描速度为4.5 mm/s时,在进行较大空间的磁场测试时会因为扫描速度过慢,降低测试效率。因此,为了减小对测量结果影响的同时提高测量效率,后续测量中将采用9.0 mm/s的扫描速度进行测试。

3.3 磁场均匀性为1%区域的理论与试验对比

在测量磁场均匀性试验中,环境噪声约为17 dB,磁场传感器扫描速度为9 mm/s。

为达补偿地磁场的目的,通过调节X、Y、Z轴3个方向线圈的电流,使得磁场传感器每个方向的磁场与将其置于磁屏蔽筒中的磁场基本上一致,经调节后X、Y、Z轴3个线圈电流分别为0.085、0.039、0.002 A。利用式(1)～(9),计算空间磁场分布并绘图。图10为理论计算结果示意图。图11为试验测试结果示意图。

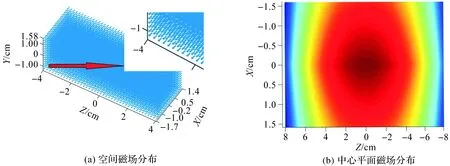
图10 理论计算结果示意图Fig.10 Schematic diagram of theoretical calculation results

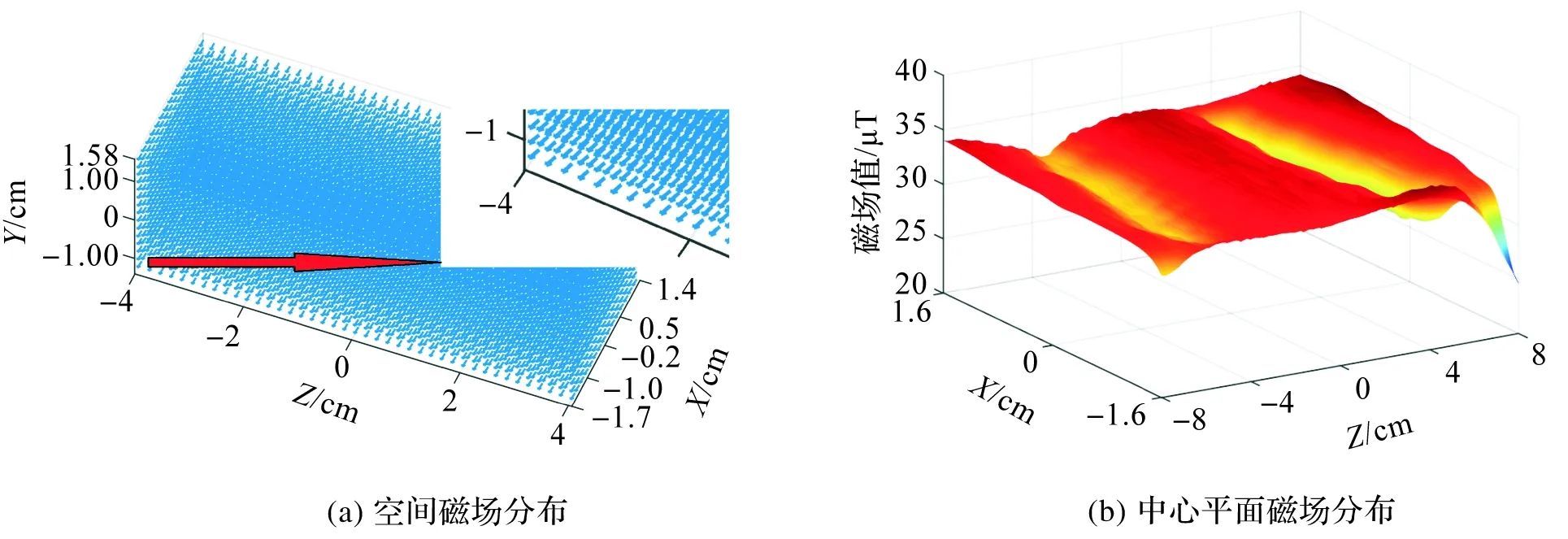
图11 试验测试结果示意图Fig.11 Schematic diagram of experimental test results

对比图10(a)与图11(a),在直径为3 cm、长度为16 cm的圆柱形测试空间中,图10(a)和图11(a)均展示其中8 cm×2.8 cm×2.8 cm的长方体区域内磁场分布。将3个方向电流代入式(1)～(9)中计算,可得磁补偿系统空间中心点理论磁场为32.97 μT,试验测试得到的磁场为32.80 μT,理论值与试验值间误差为0.21%,说明磁补偿系统空间内理论磁场与试验测试磁场基本上一致。

由图10(b)与图11(b)可知,磁补偿系统中心区域存在一个磁场均匀区。利用式(6)可计算出空间磁场均匀性在1%内的区域。在直径为3 cm、长度为16 cm的测试空间中,利用网格法经理论计算得到磁补偿系统中心磁场为零,且均匀性在1%内的区域达到该空间的49.32%;在试验测试中,磁补偿系统中心能实现0.079 μT的近零磁场,而地磁场强度约为30 μT～70 μT,经计算该装置补偿精度大于99.74%。通过分析试验数据得到主动补偿后零磁空间范围为直径为2.92 cm、长度为7.6 cm的圆柱空间,该区域内磁场均匀性小于1%并达到了整个测试空间的44.84%。由试验测得的空间中1%磁场均匀区范围与理论值49.32%相比误差为4.48%,出现该误差的部分原因可能是制作工艺与试验条件的限制。

综上所述,所研究的三维均匀磁场主动补偿系统,其中心区域能够实现产生均匀磁场且补偿包括地磁场在内的环境磁场的功能。

4 结 语

环境扰动是影响磁补偿系统内部磁场波动及测量结果准确性的一个重要因素;同时,在进行测量时需要选择合适的磁场传感器扫描速度,当环境噪声低于17 dB且磁场传感器扫描速度不高于9 mm/s时,对测量结果影响较小且能保证测量效率。经理论计算,在直径为3 cm、长度为16 cm的圆柱测试空间中,系统中心磁场为零,且磁场均匀性在1%内的区域达到该空间的49.32%;经试验测量,系统中心能够实现0.079 μT的近零磁场,且磁场均匀性在1%内的区域达到测试空间的44.84%,试验结果与理论值相比误差为4.48%。因此,本磁场补偿系统能够产生均匀磁场且实现补偿地磁场的目标,从而为基于零磁空间的相关研究,例如心磁、脑磁测量、材料缺陷检测、生物行为变化等应用提供了理论基础和实践参考。