基于土-桩动力相互作用的大跨度钢管混凝土拱桥地震响应分析

周忠浩

(西南交通大学土木工程学院，四川成都610031)

随着我国川藏铁路、西部陆海新通道等的规划和建设，川藏地区的铁路公路交通路网将得到飞速发展，由于川藏地区多大河深谷，建设规划的桥梁数量将急剧增加，与此同时据统计2008年1月—2021年2月期间，我国共发生6.0级以上地震107次，其中25次发生在川藏地区，可见川藏地区地震断裂带十分活跃，地震频发[1]，因此在进行相关桥梁设计时应高度重视桥梁抗震性能。另一方面土-桩动力相互作用对桥梁等结构动力响应影响巨大[2-3]，因此分析地震动输入方式和土-桩动力相互作用对大跨度钢管混凝土拱桥梁结构的地震响应影响意义深远。本文以川藏地区某大跨度钢管混凝土拱桥为研究对象，分别建立了桩土模型和固结模型，研究不同地震波输入下土-桩动力相互作用对大跨度中承式CFST拱桥的地震响应规律，为同类桥型的抗震设计提供参考。

1 工程概况

该桥为中承式钢管混凝土拱桥，桥跨布置为80 m+368 m+80 m，中跨计算跨径356 m，矢跨比1∶5，拱轴系数1.543，计算矢高71.2 m。边拱采用混凝土箱型拱肋，拱轴系数1.543，计算矢高17.412 m，矢跨比1∶8.5。该桥的主拱肋为8根φ1 000 mm,壁厚30～18 mm的钢管，钢管内灌注C50高强混凝土，上、下弦杆间设置钢管作腹杆，并设置水平向连接的平联杆组成桁式拱肋；立柱采用内灌注C50混凝土的圆截面钢管，主桥桥面采用6根工字型钢纵梁连接钢横梁，桥面板采用预制钢筋混凝土π型梁，通过横梁、纵梁、吊杆和立柱，与拱肋连成一体[4]。全桥共有桩基80根，①、②号主墩均采用26根φ2.5 m长度为70 m的钻孔灌注桩，余下桩基的桩径是φ1.5 m和φ2.2 m，承台为工字形，长30.1 m宽29.5 m高5 m，封底混凝土2 m。全桥桥型立面如图1所示。

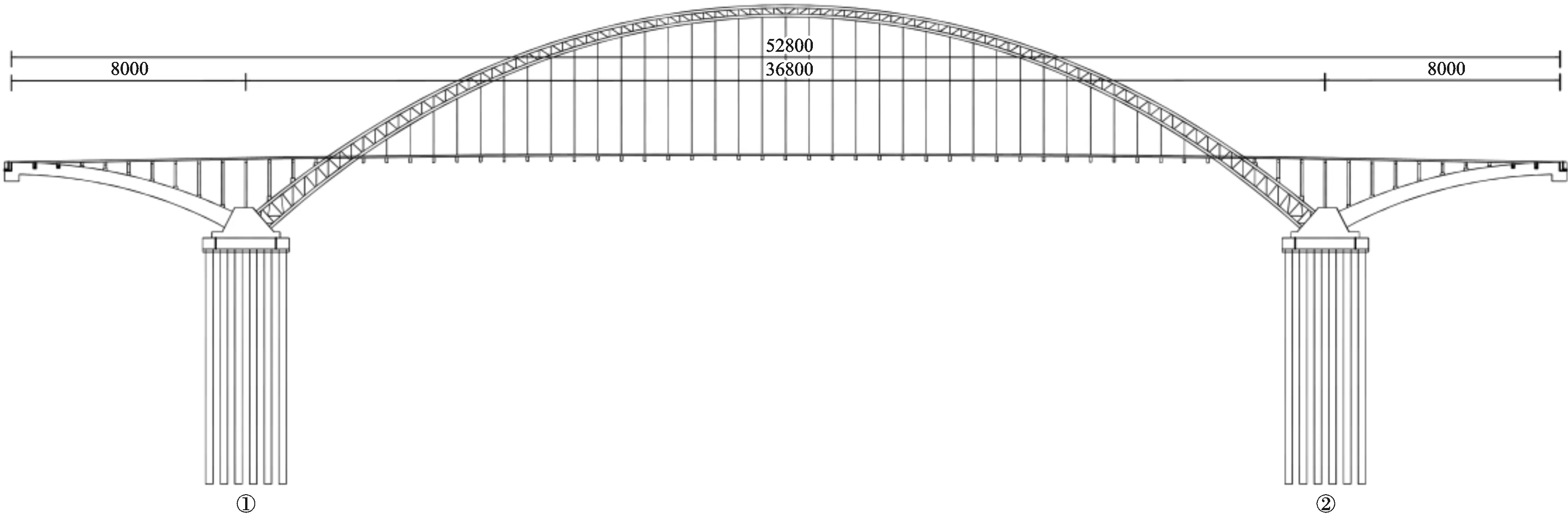
图1 桥梁立面(单位:cm)

2 空间有限元模型及参数确定

在大型有限元软件ANSYS中建立拱桥动力分析模型，对主梁的离散采用三主梁体系。在图2(a)固结模型中，上部结构弹性杆件(主拱肋、横向系杆等)采用空间线性有限应变梁单元BEA M188模拟，采用空间杆单元link10模拟吊杆和系杆并考虑其张拉效应，横梁和立柱模拟为铰接状态，采用ANSYS中的CP耦合功能模拟成主从关系。边拱处约束其绕横桥向的转动自由度，拱座边墩墩底固结，即约束其平动及转动自由度。

在图2(b)模型中，由于承台刚度较大，将承台近似处理为刚性区域，桩基础并为一根处理，与承台之间采用刚性连接，边墩处理同固结模型。在考虑土-桩动力相互作用时，假定土层为弹性介质，采用并联弹簧-阻尼单元CO MBIN14模拟，土弹簧在每根单桩上按2.0 m等间距布置。土弹簧刚度按JTG/T2231-01-2020《公路桥梁抗震设计规范》中的“m”法取值[5]。表达为式(1)：

KZ=mzb1

(1)

式中：KZ为弹簧的水平计算刚度；m为非岩石地基水平抗力系数的比例系数；z为桩节点深度；b1为桩的计算宽度。

本文采用Berger等提出的公式计算动力作用下单位桩长的辐射阻尼系数[6]，如式(2)：

c=AρVs

(2)

式中：A为桩节点之间的从属面积；ρ为土体密度；Vs为土体剪切波速。

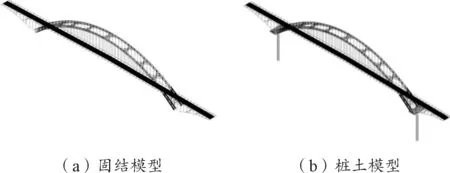
图2 2种有限元模型

3 自振特性分析

本文采用Lanczos法得到2种动力计算模型的动力特性。表1列出了该结构2种模型的前十阶自振频率与振型特征。由表1可知2种模型的基频分为0.271 4 Hz和0.251 4 Hz，小于一般的刚性拱桥，表明该桥属于中等柔性结构；该桥前二阶振动均为拱平面外的侧向振动，侧向振动影响要强于面内竖向振动，表明该桥竖向抗弯刚度大于侧向抗弯刚度，即该桥横向刚度相对较小，抗震设计时应该予以重视。考虑土-桩动力相互作用后，结构前十阶振型的频率均比固结模型的自振频率小，这说明考虑土-桩动力相互作用后，结构变柔，刚度下降，动力特性发生了一定程度的改变；2种模式下该桥前10阶振型特征并无变化，说明本桥桩基的刚度很大。

4 地震响应分析

4.1 地震动选择

根据JTG/T 2231-01-2020《公路桥梁抗震设计规范》和目前提倡的水平和竖直2个方向的抗震设计方法，应使用50年10%(50年超越概率水平10%，即E1概率)和50年2%(50年超越概率水平2%，即E2概率)2个概率水准进行计算。本文主要研究结构地震响应规律，不进行内力和位移验算，采用50年超越概率2%(E2概率)的地震参数进行抗震设计。该桥梁为A类桥梁，抗震重要性系数1.7，按Ⅶ度进行抗震设防，拟合而成的人工地震加速度时程如图3所示。

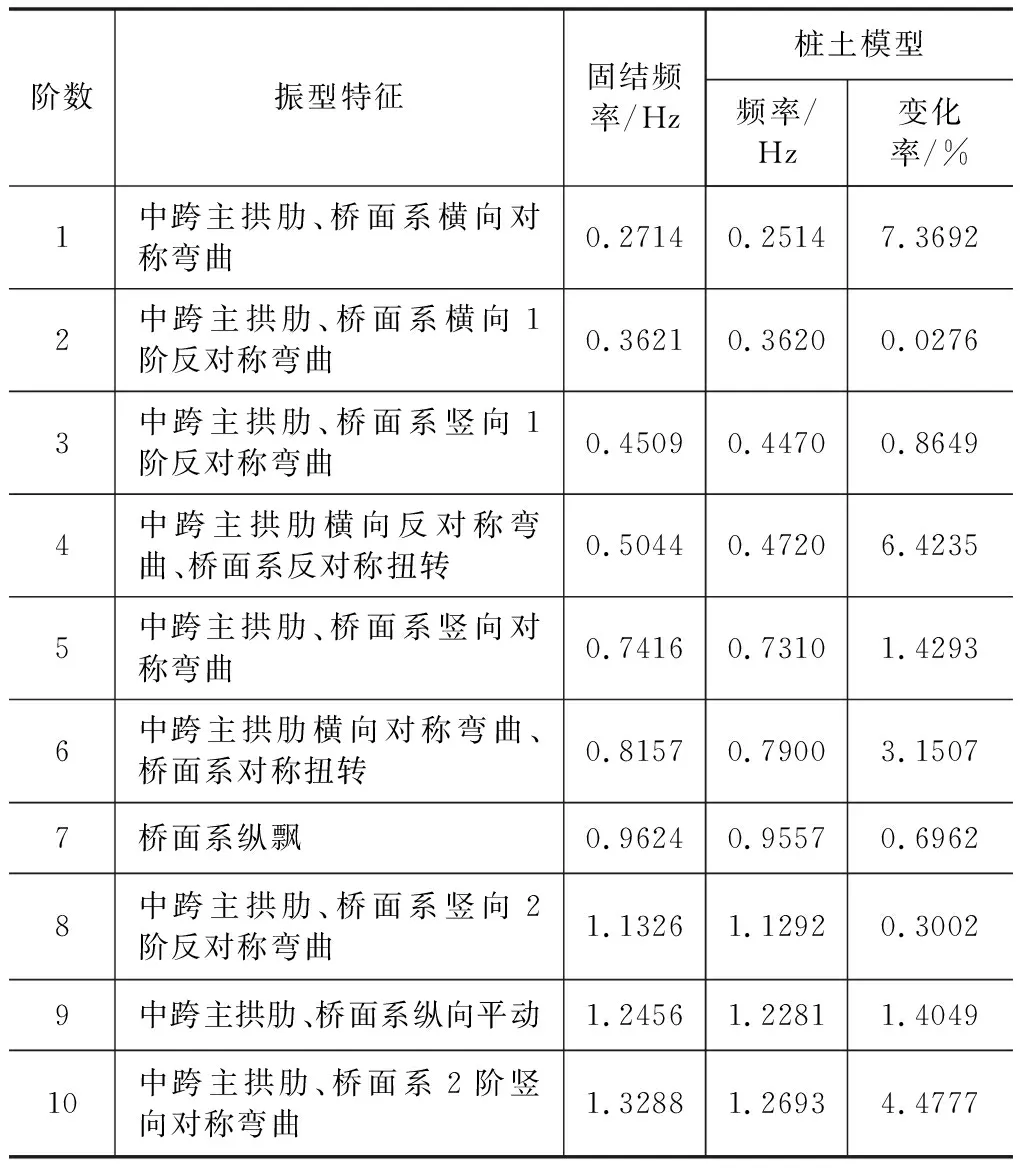
表1 2种模型前十阶频率与振型

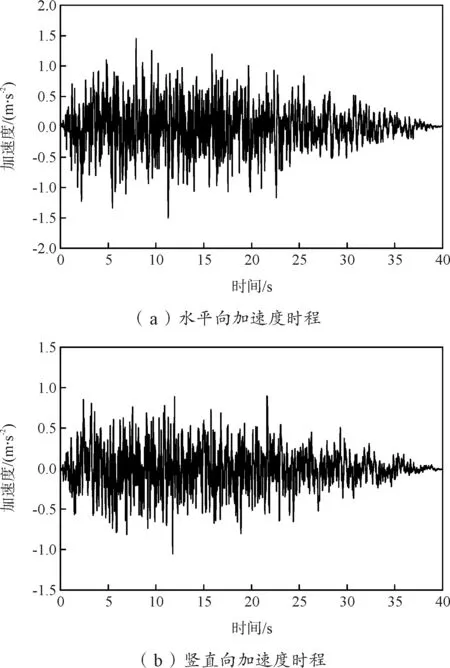
图3 人工加速度时程

4.2 地震响应分析

本文采用一致激励，共设置2种工况：①纵向输入+竖向输入；②横向输入+竖向输入。分析过程中采用ANSYS应力刚化选项考虑结构在重力荷载作用下的初始刚度，阻尼取为0.05，采用Rayleigh阻尼理论确定结构阻尼特性，地震输入时间为40 s，时间间隔0.02 s，计算结果如图4～图7所示。

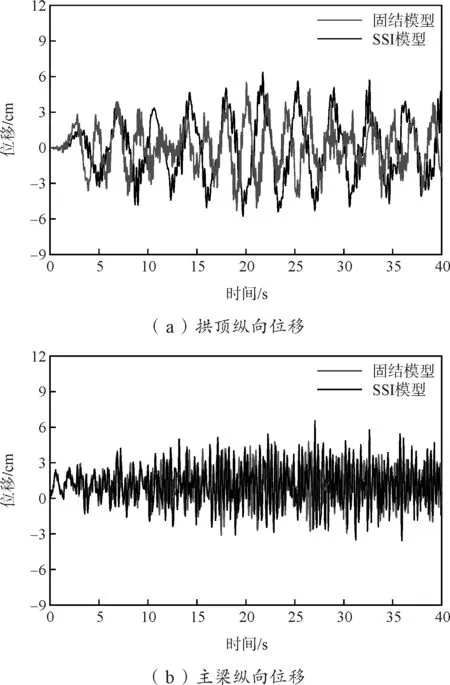
图4 位移反应时程曲线(工况1)

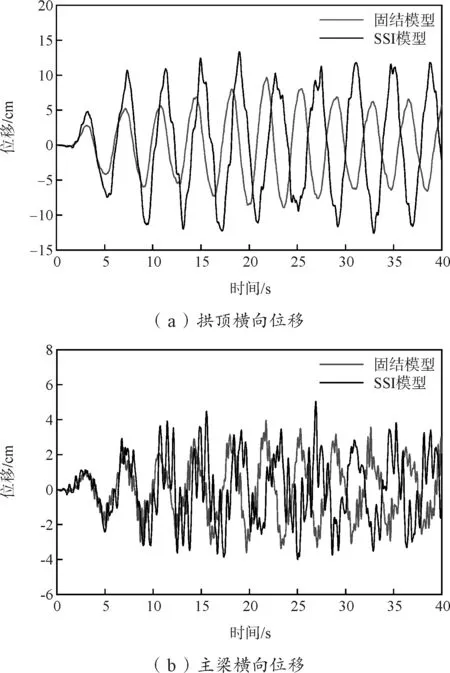
图5 位移反应时程曲线(工况2)

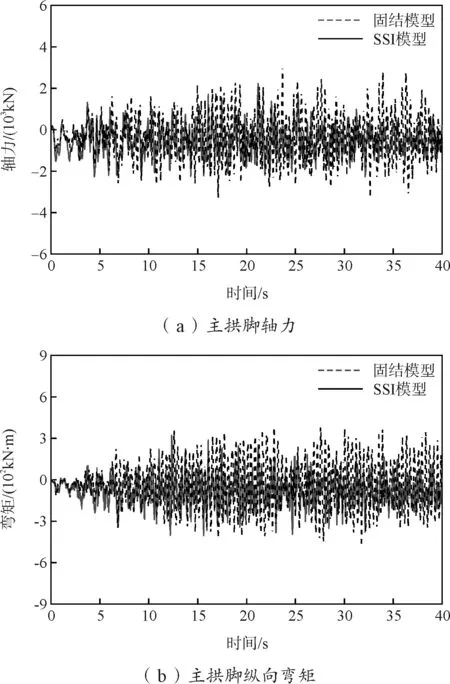
图6 内力反应时程曲线(工况1)

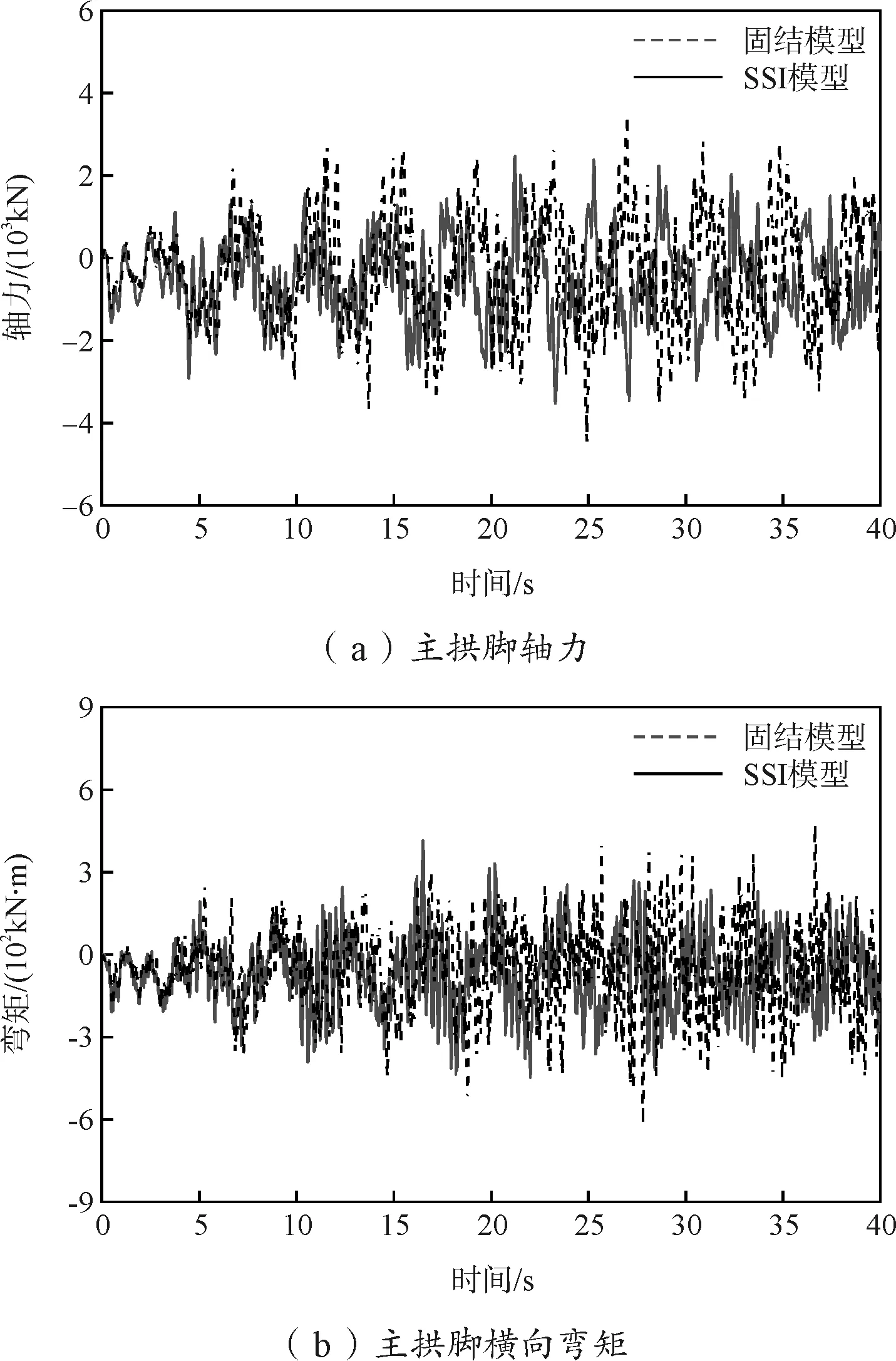
图7 内力反应时程曲线(工况2)

从图4、图5可看出：在工况1地震波激励下，固结模型与桩土模型的拱顶纵向位移分别为5.51 cm和6.35 cm，而工况2地震波激励下的2种模型的拱顶横向位移分别为9.67 cm和13.34 cm，由此说明该桥梁横向刚度较小，符合该桥梁以侧弯为主的振型特征。桩土模型与固结模型相比，考虑土-桩动力相互作用后最大拱顶纵向水平位移增加约15.2%，而最大拱顶横向水平位移增幅达到37.9%，主梁的纵向与横向位移也均有不同程度的增加，变化幅度分别为26.8%和26.7%。因此，土-桩动力相互作用对该桥梁结构的位移响应有不同程度的影响，其中对横向位移影响程度较大，即在实际工程设计时不应该将基础作为固结简单处理。

从图6、图7可看出：拱脚在横向地震作用下(工况2)内力响应更大，与自振特性分析中结构一阶振型为主拱横向对称弯曲相对应，说明该类型桥梁抗震设计中应该着重考虑其横向刚度。2种工况作用下，考虑土-桩动力相互作用的模型拱脚内力较固结模型均有减小，这是由于考虑土-桩动力相互作用后结构刚度减小，自振周期增加，土体的辐射阻尼特性增加了结构能量耗散，减小了上部结构的地震反应，因此对于该类型桥梁抗震分析，土-桩动力相互作用不可忽略。综合以上分析结果可知，2种分析模型的地震响应存在一定差异，考虑土-桩动力相互作用会使桥梁上部结构的位移响应普遍增大，也即说明如果不考虑土-桩动力相互作用将会使以结构位移为控制目标的该类型桥梁偏于不安全。

5 结论

本文以一座大跨度中承式CFST拱桥为工程背景，通过建立其固结模型与桩土模型，计算分析了2种模型的动力特性，并进行了不同地震组合工况下的时程分析，得出结论。

(1)大跨度中承式CFST拱桥是典型的中等柔性结构，与基础固结模型相比，土-桩动力相互作用使结构的自振频率变小，实际振动阻尼增加，通过影响各关键构件相对刚度，从而影响结果地震响应分配，因此考虑土-桩动力相互作用后更能准确反映出结构的动力特性。2种模型均以低频横向振动为主，可知该桥横向刚度相对较小，抗震设计时应该予以重视。

(2)在不同地震动输入下，桥梁动力响应受土-桩动力相互作用的影响各有不同，拱顶横向位移增大明显，拱脚弯矩和轴力有较大幅度较小，土-桩动力相互作用对大跨度中承式CFST拱桥地震反应的影响复杂，因此，进行该类型桥梁抗震设计应选择合理的分析模型。