公路大跨度斜拉桥独柱钢塔整体稳定性分析
2022-11-09左志超郑凯锋陈婧雯
左志超, 郑凯锋, 陈婧雯
(西南交通大学土木工程学院,四川成都 610031)
稳定问题是力学中的一个重要分支,在桥梁工程中与强度问题有同等重要的意义[1]。桥塔作为斜拉桥和悬索桥的主要受力构件,除承受由上部结构带来的巨大轴向压力外,还需承受由缆索系统带来的偏心弯矩,这一受力特征决定了桥塔是以偏心受压为主的压弯构件,其力学稳定性问题需重点关注[2]。随着桥梁跨度的不断增大,主梁和桥塔结构形式的日益多样化,以及高强度材料的应用,都会使得桥梁结构的整体刚度有所降低[3]。因此,为了确保结构安全,研究桥塔在运营阶段的整体稳定性十分必要。
近年来,大量学者对斜拉桥的稳定性问题做了一系列的研究。卜一之等[4]通过建立全桥空间有限元模型对苏通长江大桥施工全过程中结构的非线性稳定安全系数及其失稳模态进行了计算分析,研究发现结构的非线性稳定性随着施工过程呈平稳下降的趋势,主要失稳模态为索塔的纵桥向失稳及主梁的空间失稳形成的组合失稳;杨兴旺等[5]对某双塔斜拉桥进行非线性稳定性分析,并考虑了施工过程的变形和应力的叠加效应,研究发现满载布置时,结构的非线性稳定性并非最差,需合理的确定活载的布置形式以准确考虑结构的非线性安全系数;李传习等[6]对九江大桥的施工阶段和成桥阶段进行线性、几何非线性和双重非线性的稳定性分析,结果表明双重非线性稳定安全系数远低于线性、几何非线性稳定安全系数。赵雷等[7]采用LSB和ANSYS有限元软件对鄂东长江大桥施工过程进行非线性稳定性分析,研究发现施工临时荷载对大跨桥梁施工过程中的稳定性影响较小;王茜等[8]通过对钢塔节段模型进行轴心受压试验,并结合有限元程序ANSYS对钢塔进行一类和二类稳定性分析,结果表明宽厚比小的构件抵抗局部失稳的能力强于宽厚比大的构件。上述研究对大跨度斜拉桥的稳定性分析具有重要意义,但对于独柱形钢桥塔在运营阶段的整体稳定性研究分析较少。
本文以某公路大跨斜拉桥的桥塔为研究对象,桥塔为全钢结构,采用Q345qD钢,单箱多室布置,塔底到塔顶为曲线形过渡。通过MidasCivil2019建立全桥空间有限元模型,详细分析桥塔在运营阶段最不利工况下的整体第一类和第二类稳定性,为今后钢塔的设计和施工提供参考和借鉴。
1 稳定性分析理论和方法
1.1 第一类稳定
第一类稳定分析的基本方程为式(1):
([KD]+[KG]){δ}={F}
(1)
式中:[KD]为结构弹性刚度矩阵;[KG]为几何刚度矩阵;{δ}为位移;{F}为荷载。
因为[KG]和荷载的大小有关,所以随着荷载的不断增大,结构的荷载与位移不再是线性关系,当{F}达到λcr{F}时,结构呈现随遇平衡状态,这就是所要求的临界荷载。
通过推导可得第一类稳定的控制方程为式(2):
|[KD]+λ[KG]|=0
(2)
λ[KG]为临界荷载λcr{F}作用时结构的几何刚度矩阵。如果计算稳定的特征方程有n阶,则理论上存在n个特征值λ1,λ2,……,λn和对应的特征向量,但实际工程一般取最小的特征值作为第一类稳定的安全系数。
1.2 第二类稳定
第一类稳定是线性分析,发生在无初始缺陷的理想状态下,但实际结构中的初始变形,残余应力等都不在其考虑范围内,因此实际工程中一般不会用第一类稳定的安全系数来对结构进行评估。第二类稳定需要在第一类的基础上考虑几何和材料的双重非线性影响,其基本方程为式(3):
(K0+Kσ+KL)δ=P
(3)
式中:K0为弹塑性刚度矩阵;Kδ为几何刚度矩阵;KL为弹塑性刚度矩阵;δ为位移;P为荷载。
式(3)为非线性方程组,可以通过增量法、迭代法或者增量迭代混合法进行求解,当结构的整体刚度矩阵的行列式为0时,表明结构已经失稳,此时对应的荷载即为结构失稳的临界荷载。
1.3 钢桥塔整体失稳判据
JTG/T3365-01—2020《公路斜拉桥设计细则》规定斜拉桥的第一类稳定的安全系数不应小于4;对于第二类稳定则要求混凝土主梁的安全系数应不小于2.50,钢主梁的安全系数应不小于1.75。但对于斜拉桥中的桥塔,规范并未给出明确数值规定,鉴于国内已建成的大跨度桥梁的整体稳定性评估经验[3],本文最终确定将桥塔的非线性稳定安全系数定为不小于2.0。
由于桥塔的受力效应主要是由不可变荷载W和可变荷载P组成,其中W主要由恒载、索力、温度荷载、风荷载所组成,P主要是车辆活载。为准确模拟实际结构的受力状况,本文定义结构的安全系数λ为式(4):
(4)
式中:Pcr为结构的极限承载力(即临界荷载),因此本文计算所得失稳临界荷载为1倍不变荷载与λ倍可变荷载之和。
2 计算模型
2.1 工程背景
本文以一座主桥跨径布置为(50+180+500+180+50)m的双塔斜拉桥为工程背景,主桥全长960m,边跨设置一个辅助墩,上部结构采用漂浮体系。主梁采用分离式流线型钢箱梁,斜拉索采用扇形平行双索面布置的锌铝合金镀层平行钢丝。桥塔为曲线独柱形钢塔,主塔结构采用Q345qD钢,塔自塔座以上高度166m,主梁以上桥塔高度为130.693m,桥塔采用切角矩形断面,单箱多室布置,由四周壁板和三道腹板(一道横腹板和两道纵腹板)构成,桥塔截面如图1所示。塔底部断面16.0m(横桥向)×9.5m(顺桥向),塔顶截面尺寸为6.0m(横桥向)×6.5m(顺桥向),横桥侧塔柱竖向外轮廓斜率为10.87∶100,塔身通过圆弧段从塔底过渡到塔顶。
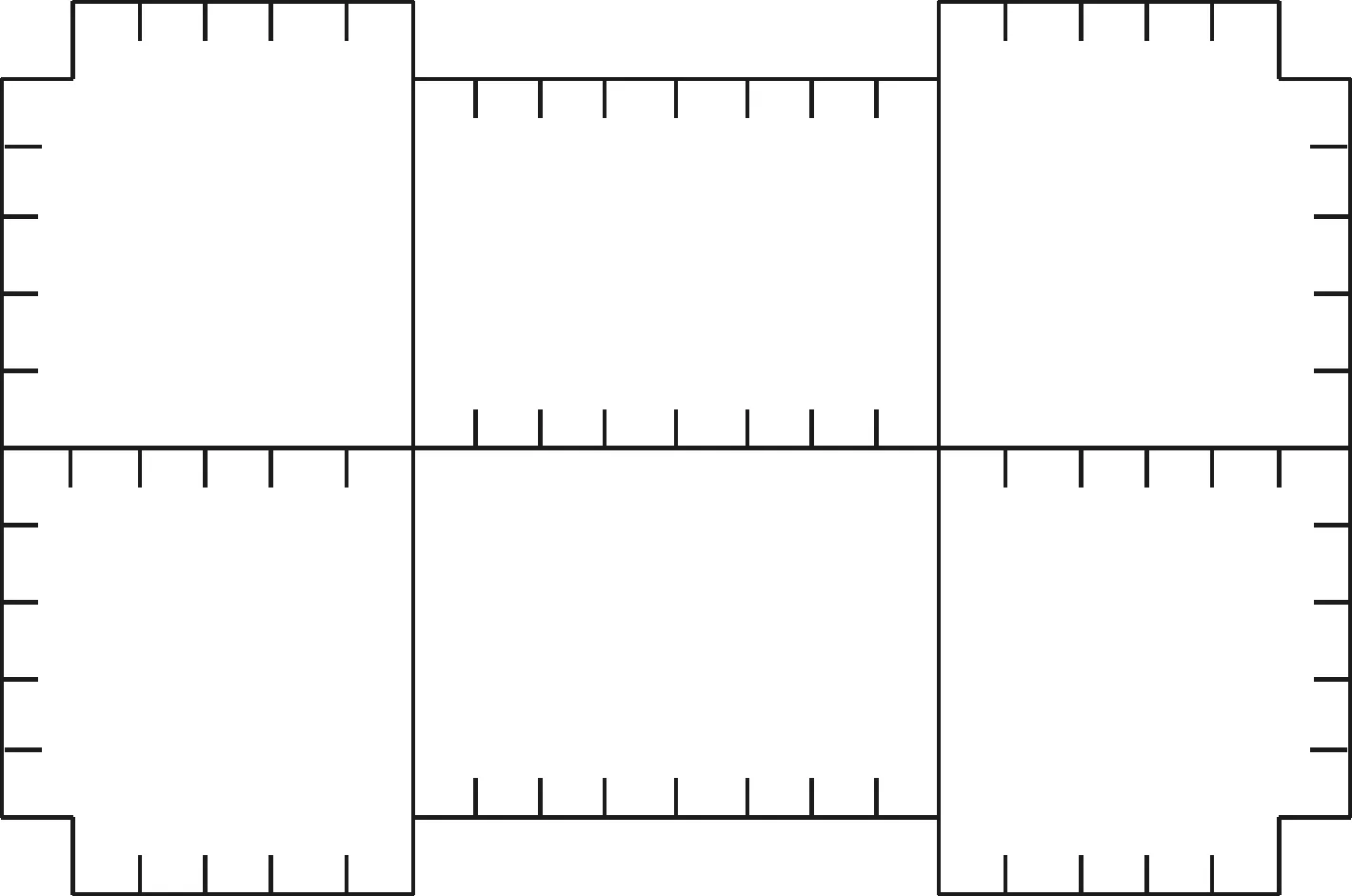
图1 桥塔截面
2.2 有限元模型
采用MidasCivil2019建立全桥空间有限元模型,主梁、索塔、桥墩、横隔板、钢横梁都采用空间梁单元,吊杆采用桁架单元,全桥共计采用了4 353个节点和4 030个单元,有限元计算模型如图2所示(简称杆系模型)。杆系模型以土弹簧单元模拟桩周围土抗力的影响,以等效弹性模量的方式考虑单向支座的影响。
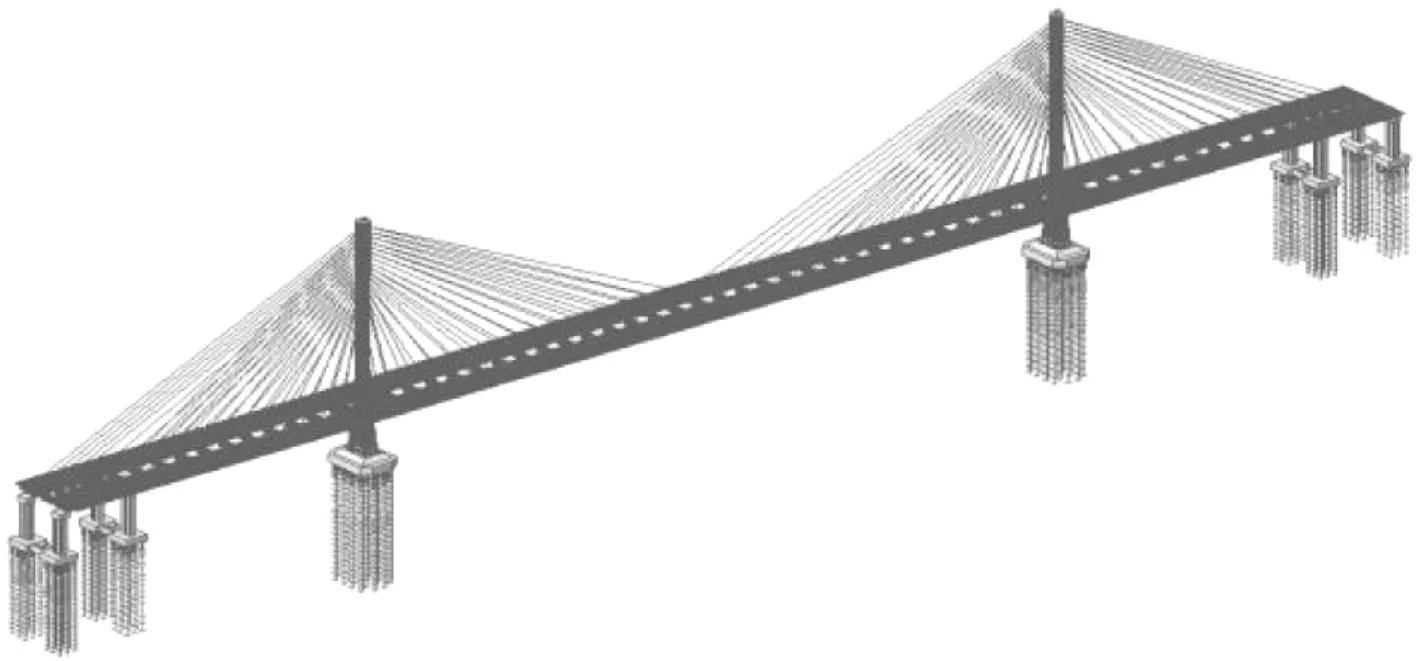
图2 全桥有限元模型
2.3 荷载工况
针对该桥在运营阶段的整体稳定性分析,本文共分4个荷载工况,如表1所示(单幅满布为近风侧箱梁单幅沿纵桥向满布活载,边跨满布为箱梁双幅沿纵桥向桥塔外侧满布活载,中跨满布为箱梁双幅沿纵桥向桥塔内侧满布活载)。荷载包括恒载,风荷载和汽车荷载,其中恒载包括自重、二期、压重和索力,汽车车道荷载JTGD60-2015《公路桥涵设计通用规范》的规定取值,集中力施加于主跨跨中。风荷载依据JTG/T3360-01-2018《公路桥梁抗风设计规范》的规定取值,主梁横向运营风取3.65kN/m,桥塔横向运营风取8.54kN/m。
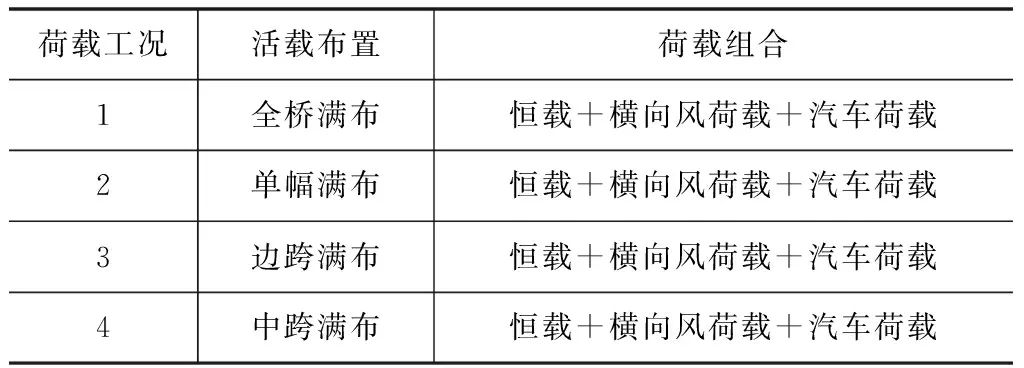
表1 荷载工况
3 弹性稳定计算分析
基于所建立的空间杆系模型对全桥进行第一类稳定分析,得到各荷载工况下的屈曲模态以及对应的稳定性安全系数。由于实际工程中,结构失稳一般表现为第一阶失稳,高阶失稳对结构的稳定性评判意义不大,因此本文只列出各工况下的全桥的第一阶失稳模态以及对应的稳定性安全系数,见表2。由于各荷载工况的第一阶失稳模态相同,因此本文只给出工况1的失稳模态,见图3。同时为分析影响结构整体失稳的主要控制因素,本文分别计算全桥在恒载、横向风荷载、车道荷载单独作用下的失稳模态及稳定性系数,见图4和表3。
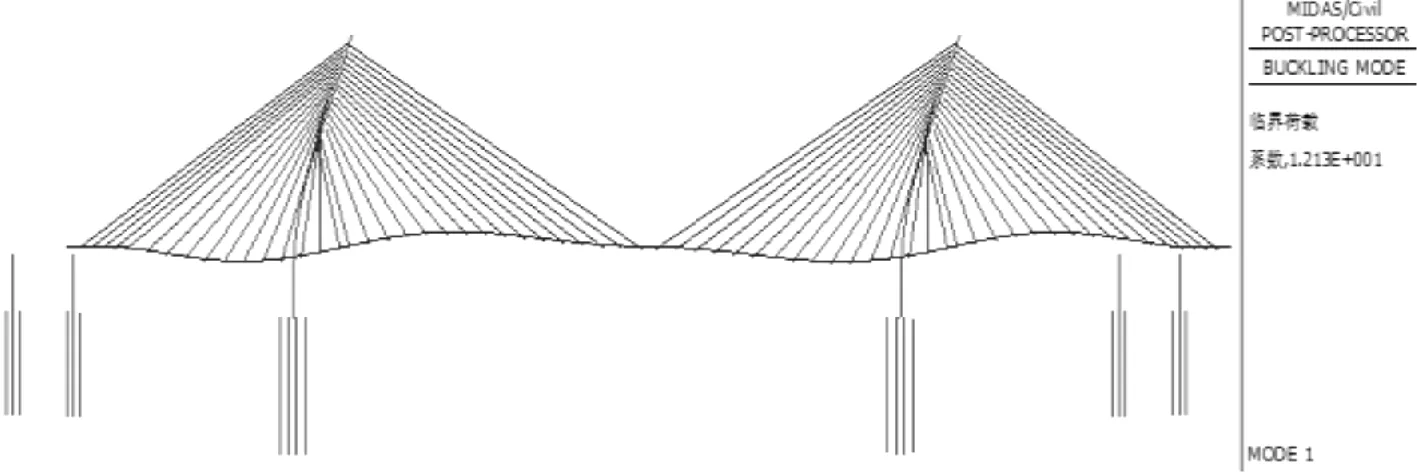
图3 工况1失稳模态
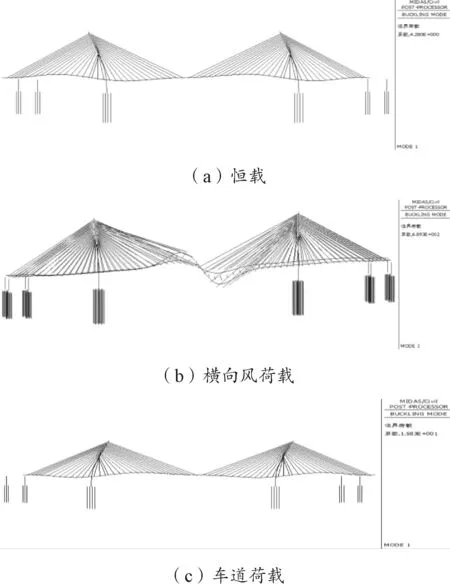
图4 各荷载单独作用全桥失稳模态
由表2可知,各荷载工况下结构的一阶失稳均表现为主梁和桥塔纵飘,与大跨度斜拉桥稳定性分析的一般结论相同[9];由图3、表3可知,恒载单独作用下结构的失稳模态为主梁和桥塔纵飘,稳定安全系数为4.3;横向风荷载单独作用下结构的失稳模态为主梁反对称扭转,稳定安全系数为689.3;车道荷载单独作用下结构的失稳模态为主梁和桥塔纵飘,稳定安全系数为15.8;由此可知,对于该桥的一类稳定而言,横风并不起控制作用,主要控制因素为恒载,失稳模态为主梁和桥塔纵飘。工况1和4的稳定安全系数较低,说明桥塔在全桥满布和中跨满布车辆荷载时易发生整体失稳,全桥的第一类稳定安全系数最小为12.21,即失稳临界荷载Pcr为1倍的恒载、风荷载与12.21倍的车辆荷载之和,满足JTG/T3365-01—2020《公路斜拉桥设计细则》规定,且具有一定的安全度。

表2 第一类稳定分析结果

表3 各荷载单独作用全桥稳定分析结果
4 几何非线性稳定计算分析
由于该桥主梁和桥塔为全钢结构,桥塔采用独柱塔形式,塔身较高,因此可能存在几何非线性效应。为明确结构在几何非线性效应下的破坏历程及最不利工况,本文针对表1的各荷载工况对桥塔进行分析,所取的几何初始缺陷乘子为1/300[10]。对于桥塔而言,由于塔顶位移最大,因此分析中主要考虑塔顶的纵向和横向位移,限于篇幅,本文只给出塔顶节点在各荷载工况下的荷载—纵向位移曲线,初始活载为各荷载工况一类稳定的临界值,计算结果见图5和表4。
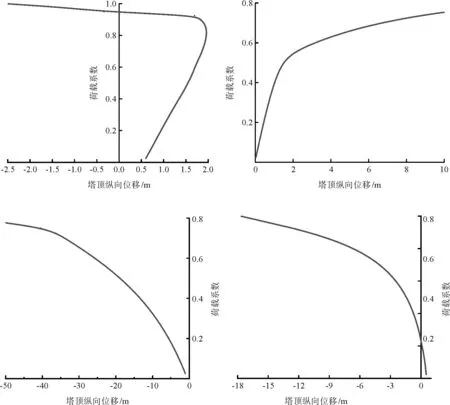
图5 工况1~4荷载位移曲线

表4 各荷载工况几何非线性稳定安全系数
由计算结果可知,全桥满布活载时最不利稳定安全系数为10.38,半桥满布活载时最不利稳定安全系数为12.08,边满布活载时最不利稳定安全系数为54,18,中跨满布活载时最不利稳定安全系数为8.77,说明在活载的布置方式中,中跨满布活载为最不利状态,其偏心效应对桥塔的非线性影响最大。
5 基于分层梁单元逐层失效模型的桥塔弹塑性极限承载力计算分析
通过引入几何非线性,计算求得桥塔的非线性稳定安全系数最小为8.77,但由于并未考虑材料的非线性的影响,因此结构可能在未达到几何非线性稳定临界值时已发生材料破坏。由于钢桥塔采用Q345qD钢,计算时采用理想弹塑性材料模型,其屈服强度为345MPa。通过考虑几何初始缺陷的影响,计算求得在最不利荷载工况4作用下右侧钢塔塔梁交界处出现最大压应力。为准确评估桥塔局部区域从加载直至屈服所承受的荷载系数,本文采用分层梁单元逐层失效的方法[11-16],引入几何初始缺陷的影响,针对桥塔在荷载工况4作用下的最不利截面所在的梁单元进行分层处理,分层梁单元的截面特性与实际梁单元的截面特性保持一致,分层梁单元模型如图6所示。
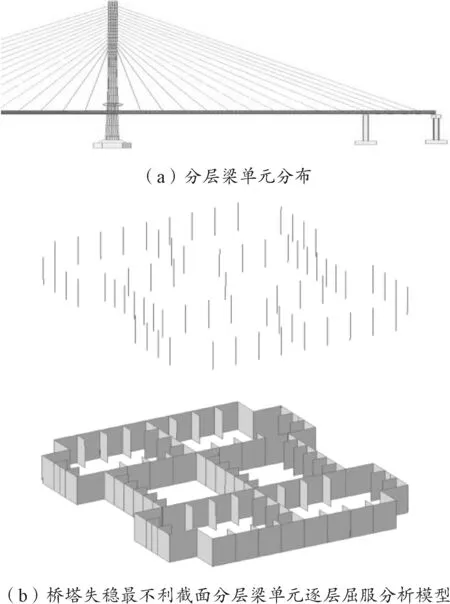
图6 分层梁单元有限元模型
采用逐步逼近的方法,保持恒载和风荷载不变,逐步增大活载系数。当荷载系数达到5.52时,最不利截面最外层梁单元开始屈服,此时分层梁单元应力状态如图7所示,最大压应力为345.05MPa,由此可确定钢桥塔的弹塑性稳定系数为5.52。
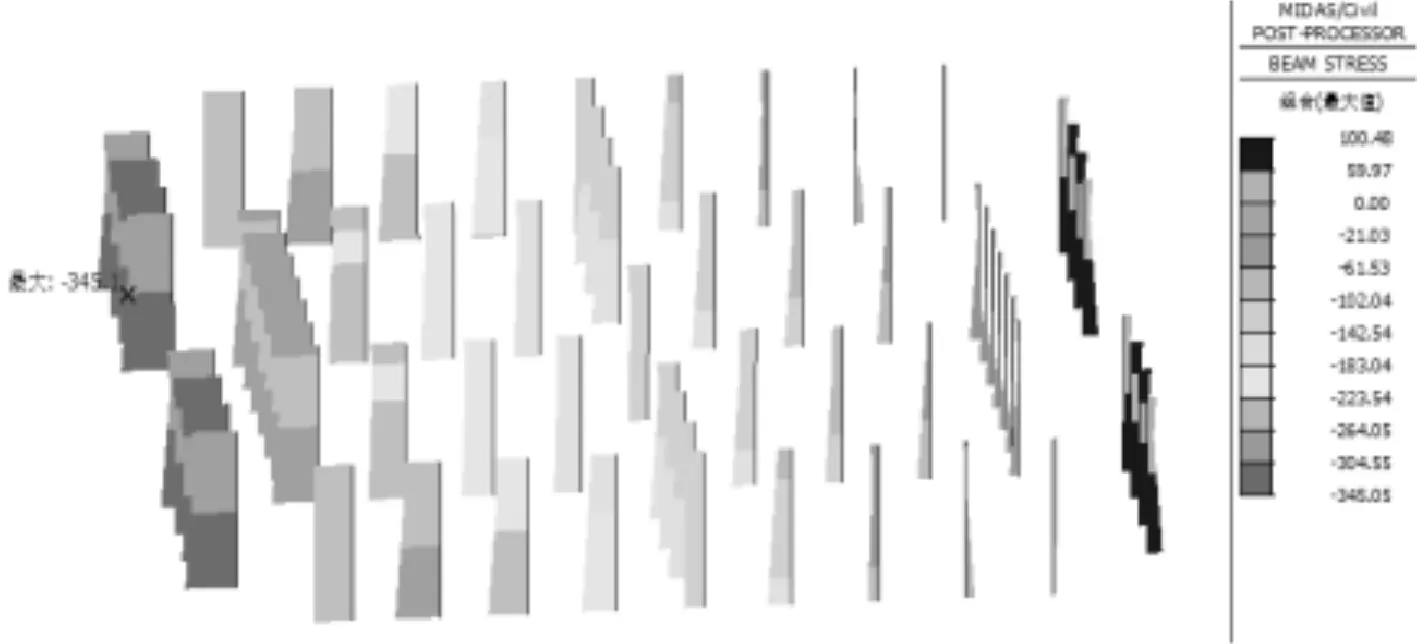
图7 桥塔最不利截面第1层梁单元达到屈服应力(单位:MPa)
当最外层梁单元率先屈服时,其余分层梁单元尚未达到屈服强度,结构仍能承载,为了进一步理解结构从加载直至达到其极限承载力这一过程,本文对荷载系数继续调整加大,直至最外侧分层梁单元全部屈服。经过逐步试算分析,当荷载系数为5.95时,钢桥塔最不利截面最外层梁单元全部进入屈服状态,如图8所示。随着荷载系数的不断增大,主梁和斜拉索的应力也在持续增加,计算结果表明当荷载系数为5.95时,主梁最大应力为213.71MPa,斜拉索最大应力为956.19MPa,均未达到其极限承载力,应力分布如图9所示。

图8 桥塔最不利截面最外侧梁单元达到屈服应力(单位:MPa)
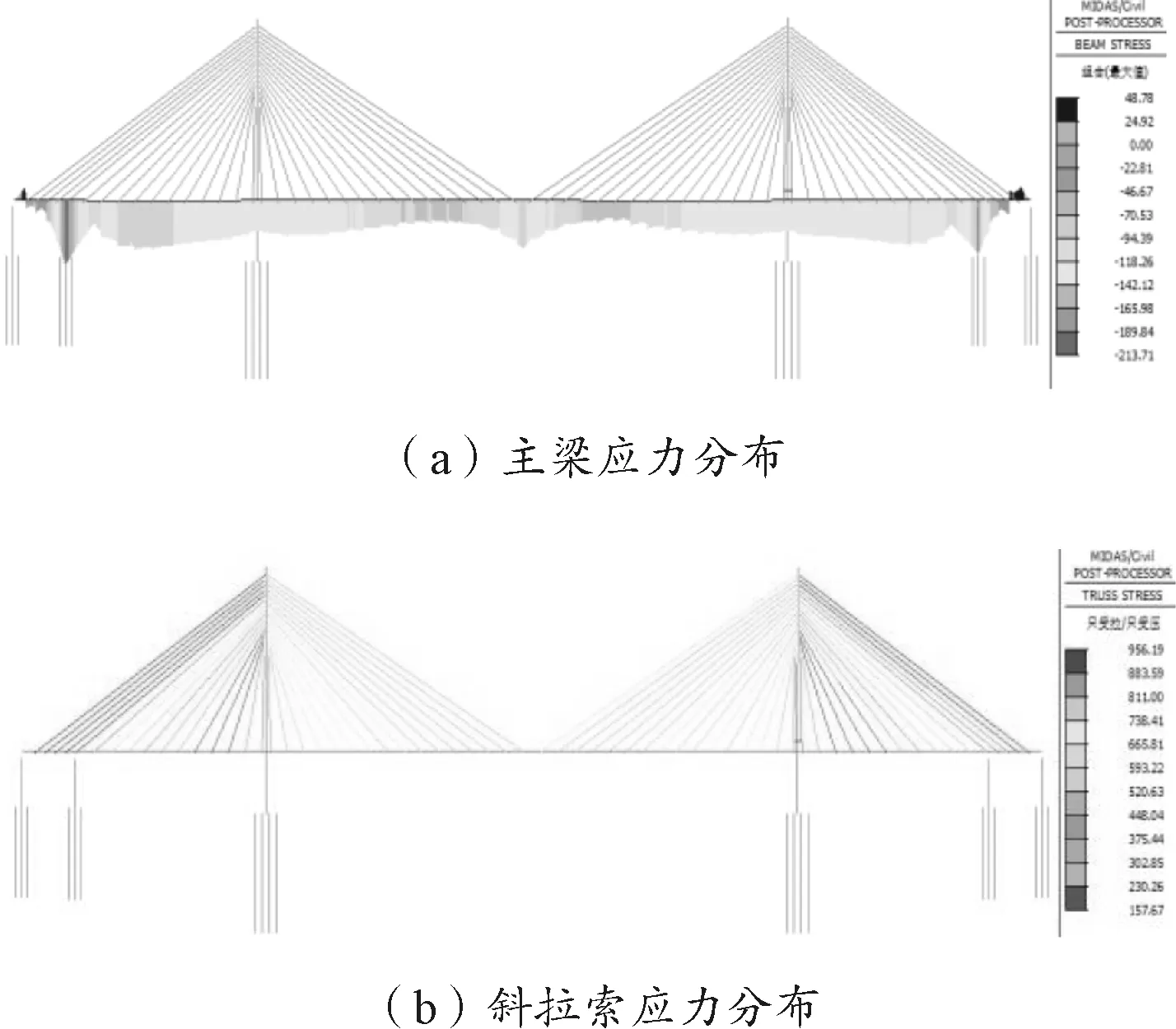
图9 主梁和斜拉索应力分布(单位:MPa)
6 小结
通过对比模型各荷载工况下结构的线性和几何非线性稳定系数(表5)可知,几何非线性对该桥整体稳定性有显著影响,考虑几何非线性后稳定安全系数都呈现出折减的趋势,最大折减50.00%。采用分层梁单元逐层失效的方法,计入几何初始缺陷的影响,分析钢桥塔最不利截面在最不利荷载工况下的弹性极限承载力,结果表明活载系数为5.52(大于设计的规定值2)时,最外层梁单元开始进入塑性阶段,活载系数小于最不利几何非线性稳定安全系数8.77,说明结构变形仍满足几何线性效应。因此该桥塔满足成桥运营阶段的整体稳定性要求。
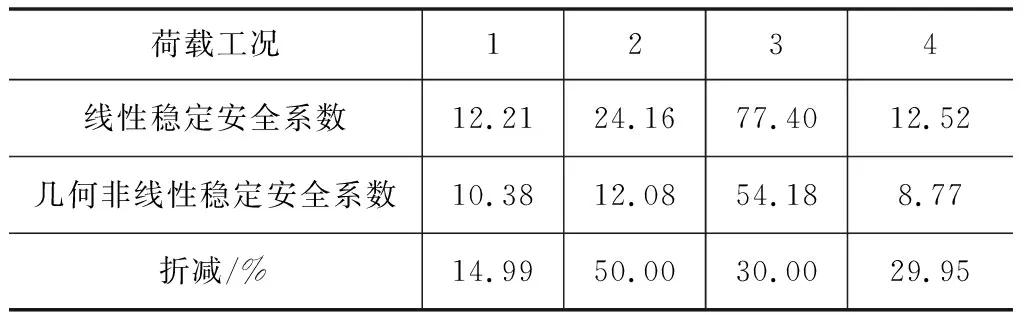
表5 稳定安全系数对比
(1)该桥一类整体稳定第一阶失稳模态为主梁和桥塔纵飘,与大跨度斜拉桥稳定性分析的一般结论相同;风荷载对一类稳定并不起控制作用,主要控制因素为恒载;线性稳定安全系数最小为12.21,满足公路桥梁规范要求,且具有一定的安全度。
(2)考虑几何非线性后,桥塔的整体稳定安全系数最小为8.77;几何非线性对桥塔的整体稳定性有显著的影响,引入几何非线性后,稳定安全系数最大折减50.00%;计入几何初始缺陷的影响,采用分层梁单元逐层失效的方法,结果表明在活载系数为5.52时,桥塔局部(右侧钢塔塔梁交接处)受力已达到屈服强度,但结构变形仍满足几何线性效应,因此该桥塔满足整体稳定性要求;随着荷载系数的不断加大,结构的应力持续增加,当桥塔最不利截面最外层梁单元全部进入屈服状态时,斜拉索和主梁应力尚未达到其极限承载力。
(3)在第二类稳定性分析中仅考虑了几何非线性的影响,对于材料特性也仅仅是在几何初始缺陷的基础上计算分析了其弹塑性极限承载力,并未同时引入材料非线性的影响,所得结果与钢桥塔在几何、材料双重非线性影响下的稳定安全系数有所偏差。
