基于多孔介质模型的养殖装备网衣水动力特性研究

陈 诚，宋炜，谢正丽,王磊，刘永利

(1 中国水产科学研究院东海水产研究所，上海 200090；2 上海交通大学海洋工程国家重点实验室，上海 200240；3 中国水产科学研究院渔业机械仪器研究所，上海 200090)

近年来，海上养殖业逐渐由近海向深远海发展，但深远海海域的海况复杂恶劣且难以预测，在极端条件下会对结构物产生巨大的载荷作用。网衣作为养殖装备的重要组成部分，对其水动力特性的研究对于了解养殖装备的水动力响应具有重要意义。

研究人员对网衣的水动力特性进行了大量的实验探究，如Zhan等[1]，李玉成等[2]，Lader等[3-4]，宋伟华等[5]，Patursson等[6]，这些研究主要聚焦于雷诺数、密实度、来流攻角等参数对于网衣阻力和升力的影响，并根据实验结果拟合出一系列网衣阻力和升力的经验公式。此外，Kristiansen等[7]〗开展了风浪下网箱系泊特性的研究，Bi等[8]，曾启东等[9]从波浪和网衣参数的角度对网箱的阻尼特性开展了研究。

随着CFD的发展，多种数值模型逐渐发展并被应用于网衣水动力的研究上。Van等[10]最早发展了基于Navier-Stokes方程的多孔介质模型，并将其应用于近岸多孔结构的研究上，此后，多孔介质模型在其他学者如Nakayama等[11]、赵云鹏等[12-13]、Jensen等[14]、Bi等[15]的研究中不断完善与扩展。与此同时，Morison模型和Screen模型被应用于网衣水动力模型的构建，Tsukrov等[16]构建了基于修正Morison方程的网衣水动力的有限元模型，Chen等[17]提出了一种基于Morison载荷模型的多孔介质阻力系数计算方法，Kristiansen等[18]提出并讨论了粘性水动力的Screen模型。此外，集中质量法(Huang等[19]，Martin等[20])、有限体积法(Zhao等[21-22])、流体体积法(Jafari等[23])、有限元法(崔勇等[24])等也被广泛应用于网衣水动力研究中。在数值计算的载体上，由Jensen等[14]，Feichtner等[25]在OpenFOAM软件中开发了基于多孔介质模型的计算框架，以此为基础开展数值研究。

然而，在现有的网衣水动力研究中，绝大多数以规则波作为输入，无法体现出深远海中所可能面对的极端海况。为此，需要采用一些有代表性的不规则波来模拟极端海况。Xu等[26]在波浪水槽中进行了一系列极端波的实验，得出密实度和KC数是影响网板作用力的主要参数。俞嘉臻等[27]将聚焦波与网衣相互作用，分析了不同网衣参数对升阻力特性的影响及对波浪场的扰动规律。新波理论(NewWave)从概率统计的意义上代表了波峰附近最可能发生的波浪时历，既包含了波浪谱的特征信息，又能有效减少数值模拟的时间[28]。

针对波浪与网衣结构的相互作用展开研究，将多孔介质模型引入网衣系统，使用Morison模型对网衣进行力学分析，并通过等效分析得到了多孔介质阻力系数的直接估计方法。数值模拟过程在开源CFD软件OpenFOAM中进行，并使用造波工具箱waves2Foam实现规则波和聚焦波的模拟。基于数值模拟的结果，通过参数化分析研究了影响网衣所受阻力的因素以及网衣对波浪场的影响。最后，为寻求一种对极端波浪下网衣多孔介质阻力的有效预报，根据已有的数据总结给出了网衣水动力载荷的预测模型。基于本文的研究可以对网衣的设计与装配提供理论参考。

1 网衣水动力模型

1.1 多孔介质模型

本数值模拟研究在开源CFD软件OpenFOAM中展开，采用了有限体积离散化的方法，求解了体积平均、雷诺平均的N-S方程(即VARANS方程)。Jensen等[14]给出了详细的推导过程，其最终的连续性方程和动量方程如下：

(1)

(2)

(3)

式中：cij为非线性阻力系数矩阵。

流体对网衣的作用力即为(3)式所表征流体所受阻力的反作用力，其合力可由每个微元的受力的积分得到：

(4)

式中：PV为多孔介质区域的体积，cij是未知的，将在1.2节中使用Morison载荷模型进行等效得到。

1.2 Morison模型

在Morison模型中，将每一根网线视为一个独立的圆柱体进行分析，不考虑结节的影响，并利用Morison方程来计算其上所受的作用力。由于网衣的孔隙率较高，在研究中忽略了网线间的水动力影响。因而，作用在整个网面上的合力可由每根网线上的力叠加得到。

如图1所示，假设网衣在y-z平面内，网面的法线沿x方向，网目的基本单元由横向的网线1及垂向的网线2组成。

注：U∞为来流速度，Uxy为来流速度在xoy平面内的分量，Uz为来流速度在z方向上的分量

来流速度为U∞，其分量Uxy=U∞cosβ，Uz=U∞sinβ。x-y平面内的来流与网衣相对方位图如图2所示。

注：Uxy为来流速度在xoy平面内的分量，Fxy为波浪对网线的作用力

对于网线1，流速Uxy可分解为切向分量和法向分量，其中切线分量引起的摩擦力是一个小量，可忽略不计，流速Uz引起一个z方向的力，因此网线1主要受法向力作用，则其所受力大小为：

(5)

Fy,1=0

(6)

(7)

对于网线2，流速Uxy沿网线的法向，流速Uz与网线平行，则其所受力大小为：

(8)

(9)

Fz,2=0

(10)

式中：Cd为网线的阻力系数，A1,A2等于网线1在y-z平面内的总投影面积。

则作用在网衣上的合力就是每根网线受力的叠加

(11)

(12)

(13)

式中：M,N分别为平行于网线1、2的网线根数。

又由1.1节得，作用在多孔介质结构上的力为：

(14)

(15)

(16)

式中：c1,c2,c3分别为x,y,z方向上的阻力系数，V为网衣的体积，网衣是一种高孔隙率的多孔结构，波浪流经网衣前后，流速的降低并不明显，因此可以认为网衣附近的流速Uxy等于远处的来流速度U∞。

由于作用在网衣上的力F等于每根网线受力Q的叠加，将二者列为等式，即可得到阻力系数C1,C2,C3的表达式：

(17)

(18)

(19)

则基于多孔介质模型的网衣受力如下：

(20)

(21)

(22)

Chen等[17]通过对前人实验结果的总结，给出了在一定密实度范围内，系数a和b的参考值如下：

(23)

(24)

在本研究中，波浪沿x轴正方向垂直于网衣入射，即攻角θ=90°，则网衣受到沿x方向的阻力Qx以及z方向的升力Qz，y方向受力为0。

1.3 阻力系数等效选取

Lader等[3]通过多组网衣实验得到了不同波浪与网衣相互作用后网衣阻力数据。Chen等[17]对其进行了整理，得到了对应的网线阻力系数cd的数据。圆柱形网线的阻力系数受波浪的流态影响，可以认为主要与雷诺数Re和KC数有关，二者的表达式如下：

(25)

(26)

式中：U为波浪的特征速度U=Aω，即波幅A与圆频率ω之积，v为运动粘度，T为波浪周期。

为此，可将网线的阻力系数视为Re和KC的函数，用多参数拟合的方法拟合数据，并用于内插法取值，拟合结果如图3所示。

注：cd为网线阻力系数，Re为雷诺数，KC为KC数

2 数值模拟方案

2.1 数值水池

二维数值水池的参数根据波浪和网衣的参数来决定。如图4所示，其中水池总长为5.5λ，水深1λ，满足深水条件，其中λ为波长。左侧边界为造波板，所产生的波浪向x轴正方向传播，在4～5.5λ的范围内设置了消波区，用于吸收波浪，减少波浪反射的影响。

图4 数值水池示意图

网衣高1 m，厚0.05 m，被竖直放置在距造波板2λ的位置，一半被浸没在水中，在数值模拟中测量网衣前后1λ范围内的波浪时历以及网衣处的多孔介质阻力及升力。

1.5 模型有效性验证

为验证所建立模型的有效性，在OpenFOAM中建立与Lader等[3]所做试验相同的水池模型，使用相同的波浪、网衣参数进行数值模拟，对比分析波浪时历η、网衣处的阻力Qx、升力Qz等数据，结果如下。

由图5可知，数值模拟的结果与试验结果比较接近，阻力误差的主要来源可能在于试验中网衣的变形等不确定性在数值模拟中并未被考虑，但由结果来看模型的准确性已基本满足要求。

注：周期T=0.70 s，波幅A=0.022 m

3 数值模拟研究

3.1 规则波数值模拟

3.1.1 密实度的影响

密实度Sn描述着网线投影面积占网衣总面积的比值，在海洋环境中，随着时间的推移，各种藻类、砂砾等会附着在网衣上，这将改变网衣原有的密实度，对网衣的水动力特性产生影响，因而研究密实度对网衣载荷的影响有重要意义。密实度主要从两个方面来影响波浪的传播。一方面，随着密实度的增加，渔网在波浪方向上的有效面积增大，从而增加了对波浪传播的阻碍作用；另一方面，随着密实度的增加，波浪与网衣的相互作用面积增大，因此，摩擦所引起的波浪能量耗散也越大。

采用同一波浪与四种不同密实度的网衣相互作用，数值模拟参数和结果见下。

表1 网衣参数

注：周期T=0.80 s，波幅A=0.02 m

由图7可知，在一定的密实度范围内，网衣所受的阻力随着密实度的增大而增大，二者近似呈线性关系。当密实度大到一定程度，网衣阻力与密实度之间显示出非线性关系。

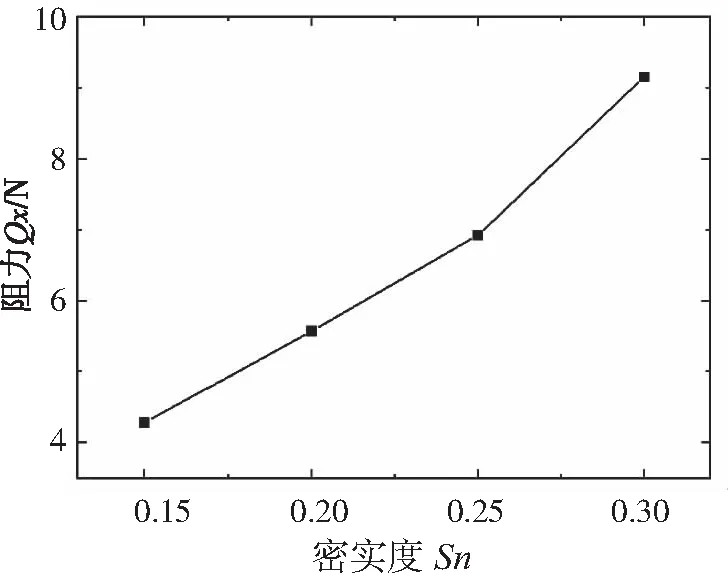
图7 阻力Qx与密实度Sn关系图

3.1.2 特征速度的影响

流速是影响网衣阻力的重要参数，然而，在实际情况下网衣各处的流速存在差异且难以捕捉，为此，需要找出一个具有代表性的速度来进行网衣的阻尼特性研究。

流体力学中的很多无量纲常数计算中都包含着特征速度U=Aω，即波幅A与波浪圆频率ω的积，它能够从幅值和频域两个角度来表示流场的信息，并且不受结构物的影响，容易得到。为研究特征速度对阻力的影响，使用相同圆频率、不同波高的规则波与网衣相互作用，数值模拟的参数如表2所示，测得不同特征速度下的阻力时历如图8所示。

注：网目尺寸D=0.016 m，网线直径dω=0.001 8 m，密实度Sn=0.225

表2 波浪参数

由图9可知，随着特征速度的增大，网衣的阻力逐渐增大。当波长一定时，随着波高的增加，水粒子的速度增大，从而导致了粘性阻力的增大，波浪力的增加表明了波浪与网衣的相互作用更为剧烈，能量耗散得越快，在3.1.3节中将会对波浪透射系数的影响因子做进一步探究；此外，随着波高的增加，网面对波浪的有效面积增大，也会使网衣对波浪的阻尼作用增强。

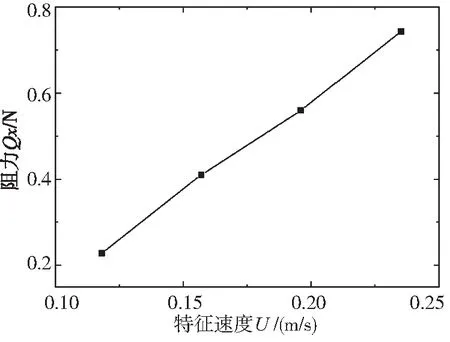
图9 阻力Qx与特征速度U关系图

3.1.3 网后波浪透射系数

网衣对波浪的阻尼作用会导致波能的部分消耗，由水波理论可知，谐波的能量正比于波幅的平方，波幅的大小体现了能量的大小。定义了一个波浪透射系数β[29]，其数值等于规则波与网衣作用稳定后网衣后1λ处与无网衣时同一位置处的平均幅值之比。在流体与结构物的相互作用中，波长与结构物特征长度的比值具有重要影响，当波长与特征长度差不多时，波浪流经物体主要体现为绕射；当特征长度远小于波长时，结构物的存在对波浪的影响很小。对于网衣来说，网线的直径dW为特征长度，现对波浪透射系数同网绳直径与波长的比值dW/λ的关系进行研究，数值模拟的参数如表3所示，测得不同dW/λ下的波浪时历如图10所示。

注：网目尺寸D=0.016 m，网线直径dω=0.002 m，密实度Sn=0.25

表3 波浪参数

由图11可知，随着网线直径相对值的增大，透射系数有下降的趋势，表明结构物尺度与波长越接近，对波浪的阻尼作用越强，这也与特征长度与波浪作用之间的关系相吻合。在本研究中，网线直径与波长的比值均为小量，因而结果呈现出一定的线性。

图11 透射系数β与网线直径与波长比值dW/λ的关系

3.2 聚焦波数值模拟

3.2.1 能量谱特性研究

在自然情况下，波浪总是由多种频率成分组成的，聚焦波就可看作是一系列不同频率和波幅的正弦波相叠加而成，即：

(27)

式中：N为所取正弦波的个数，kj为波数，ωj为圆频率，φj为相位角，x0为聚焦位置，t0为聚焦时刻，Aj为波幅，其表达式为：

(28)

式中：Ac为谱峰波幅，δω为所取的频率间隔，S(ωj)为海浪谱，本研究中采用的是Jonswap谱，其表达式为:

(29)

式中：H1/3为有义波高，γ取3.3。

为研究网衣与波浪作用后波浪的频域变化情况，使用聚焦波为输入，令其在网衣处发生聚焦，分别测量在无网衣和有网衣情况下聚焦位置后1λ处的波浪时历，数值模拟的参数及在有无网衣条件下测得的波浪时历如图12所示。

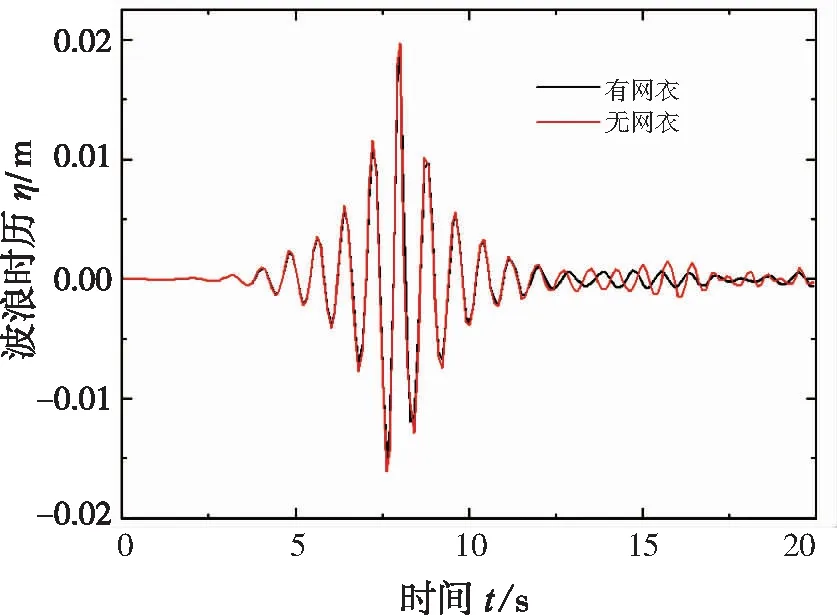
注：谱峰波幅Ac=0.02，谱峰波长λp=1 m，网目尺寸D=0.01 m，网线直径dω=0.001 5 m，密实度Sn=0.30

由图12的结果可以发现，二者在有网衣和无网衣时在聚焦位置后1λ处的波浪时历几乎相同，但在有网衣情况下的幅值小幅降低了3.4%左右，原因是波浪与网衣作用后的能量损耗，此外，在作用后的尾流也有所变化。使用FFT对两个时历做频域分析，得到二者的频域谱如图13所示。由图13可知，在小密实度条件下，波浪在与网衣作用后，波浪整体的频域分布变化不大，但有部分能量向高频发生了转移。

图13 有网衣和无网衣情况下网后1m处波浪时历的FFT分析结果

3.2.2D/λp的影响

在3.1.3节中，研究了特征长度与网线直径的比值对网后波浪透射系数的影响，但对于海洋养殖网来说，网目尺寸是一个更重要的参数，既要满足一定的间距，保证充分的水交换，还要避免所养殖鱼类的逃逸，并在此基础上，满足基本的安全性能。

为研究网目尺寸D对网衣阻力的影响，以聚焦波为输入，作用在四种网目尺寸不同的网衣上，测量网衣处的阻力，数值模拟的参数如表4所示，测得不同D/λp下的阻力时历如图14所示。

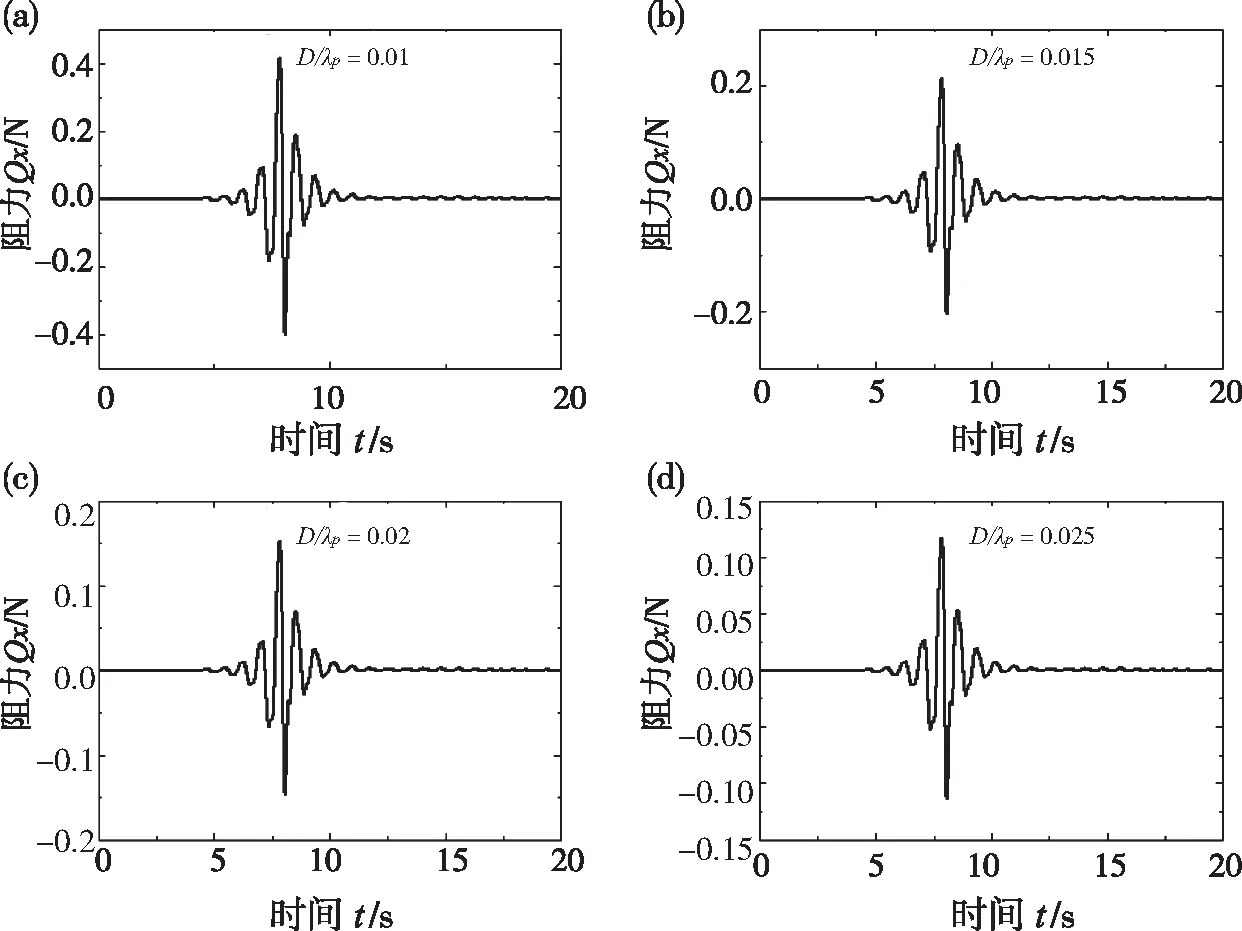
注：谱峰波幅Ac=0.02 m，谱峰波长λp=1 m

表4 网衣参数

由图15可知，在波长相等的情况下，随着网目尺寸的增大，网衣的阻力逐渐减小。这意味着从网衣出发有两种角度来降低载荷，一是增大网目尺寸，即在网衣大小不变的条件下减少网线的根数，二是在网线直径不变的情况下降低网线直径，但同时需要保证网孔的尺度不至于让养殖的鱼类通过，并且保证一定的直径来保证安全强度。

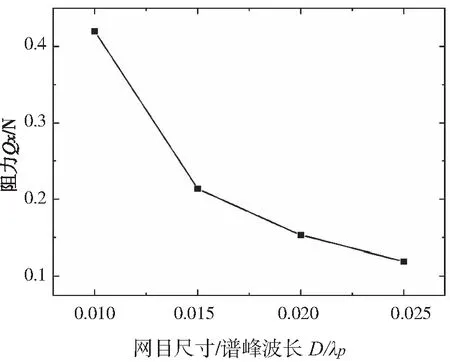
图15 阻力Qx与网目尺寸与谱峰波长比值D/λp关系图

3.3 阻力预报

在现实海况下，想要实时获取或预测网衣上所受的载荷是十分困难的，如果能够通过一些容易得到的数据，来对网衣载荷进行及时的预报，或者在预设的海况下能够事先了解网衣上的载荷分布情况，并为网衣的设计提供一定的参考，这是研究网衣水动力特性的主要目的。

通常计算网衣所受的阻力的方法是采用前人总结得到的经验阻力系数，改方法对于均匀稳定的流场比较有效，但目前针对极端波浪的网衣阻力计算和预测方法还很少。从作用的效果上看，阻力是网衣上的主要载荷，会引起网衣的形变，也是过往研究中的重点，根据之前的研究可以知道，阻力的大小与波浪特性与网衣特性均有紧密的关系。考虑来流攻角为90°的危险情况时，根据Morison模型推出的多孔介质阻力的表达式为:

(30)

从表达式看，当来流攻角不变时，对网衣阻力起关键作用的变量有多孔阻力系数、流速、网线总面积，其中密度ρ、系数a和网线总面积S是一个定值，则只需要知道多孔阻力系数Cd和流速Uxy平方的积分。

(31)

其中U为3.1.2节中定义的特征速度U=Aω，由对应海域的波浪谱计算得到，如对于本研究中的聚焦波可选取谱峰波长所对应的流速，则简化后的新多孔介质阻力公式为

(32)

在2.3节的分析中，将网线的阻力系数cd看作Re和KC的函数。

由于U即为Re和KC表达式中的U，因此同样可以将参数C看作是Re和KC的函数，通过之前的规则波和聚焦波的数值模拟，已经得到了一系列参数及其对应的阻力模拟结果，由此可以计算出相应的阻力系数C，对Re和KC，同样采用多参数拟合的方法，得到的拟合模型如图16所示。

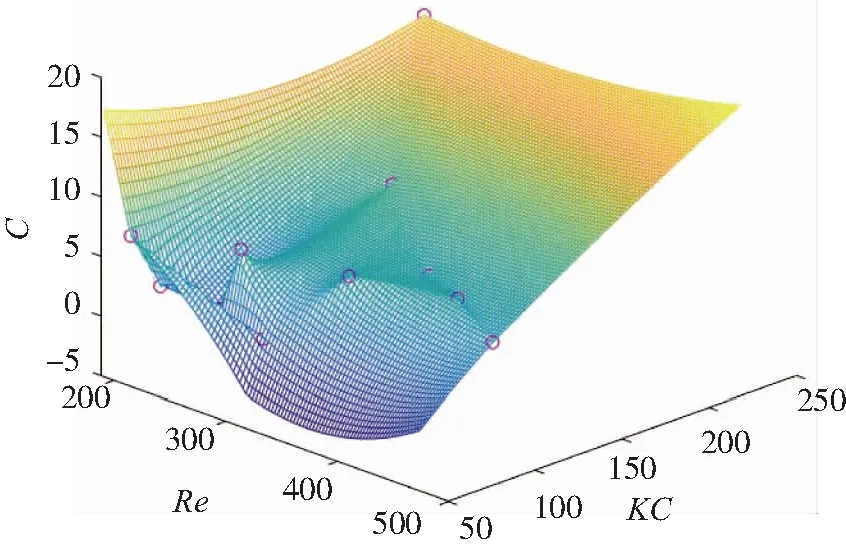
注：C为新阻力系数，Qx为阻力，ρ为密度，a为无因次参数，S为网线总面积，U为特征速度，V为多孔介质区域体积，Re为雷诺数，KC为KC数

4 结论

本研究基于多孔介质模型和Morison模型建立了网衣模型，使用OpenFOAM对网衣的水动力性能开展数值模拟研究。研究中发现，对同一规则波，随着密实度的增加，网衣对波浪的阻尼作用逐渐增强，在一定范围内两者近似呈线性关系；对不同的规则波，随着特征速度的增大，网衣的多孔介质阻力逐渐增大；随着特征长度的增大，网后的波浪透射系数逐渐增大。在以聚焦波为输入的研究中发现，在与网衣作用后，波浪的频域分布没有明显的变化，但有部分能量向高频区域发生了转移；谱峰波长一定时，随着网目尺寸的增大，网衣所受的多孔介质阻力逐渐降低。

最后，提出了一种针对极端波浪的网衣多孔介质阻力预报方法，对多孔介质阻力公式进行了简化，引入了波浪谱的特征参数作为输入，并定义了新的阻力系数，将其表示为Re数和KC数的函数，结果显示，拟合结果在取值范围内收敛，进而可以计算得到阻力，为网衣阻力的预测分析、网衣参数的设计提供一定的参考。

然而，在当前的研究中，网衣密实度的研究范围普遍在0.1～0.3的范围内，对大密实度网衣的研究还存在着很多空白；此外，对于一个典型的水产养殖网来说，Re数的范围通常在100～10 000[30]，而本研究仅限于188～471，因此还需要有更多的实验来得到更广泛的多孔介质阻力数据以完善拟合模型，得到更多定量的结论；本研究中始终保持波浪传播方向沿网衣的法向，在后续的研究中还可以将攻角的影响引入模型中。