基于Sin混沌空翻反向学习鼠群算法的路径规划

林 伟，朱豪洋

(陕西铁路工程职业技术学院工程管理与物流学院，渭南 714000)

0 引言

近年来，元启发式算法被广泛应用于求解移动机器人路径规划。研究者提出了各种各样的元启发式算法：遗传算法(GA)[1]，粒子群算法(PSO)[2]，正余弦算法(SCA)[3]，灰狼优化算法(GWO)[4]，飞蛾火焰优化算法(MFO)[5]等，虽然这些已有的群体智能算法可求解复杂的约束优化问题，但是存在求解效率较慢，优化结果精度低、易陷入局部最优等缺陷。为改善群智能算法存在的不足，研究学者们关注于如何提高算法求解实际问题的寻优性能。比如为提高求解移动机器人路径规划问题的寻优精度，引入高斯分布提出了改进的蚁群算法[6]，利用适当的"变异"操作提出了改进蚁群算法[7]，引入非线性收敛因子和结合粒子群算法的改进灰狼优化算法[8]，融合了GA和BFO变异算子提出改进的粒子群算法[10]等。相比原有的算法，改进后的算法都能够提高了算法在路径规划中的全局与局部搜索能力，可快速且稳定的获取最短路径，寻优精度和鲁棒性得到改善。

鼠群优化算法(rat swarm optimizer，RSO)[9]是一种新颖的群体智能算法，受启发于鼠群的追逐和搏斗行为，具有算法结构简单，控制参数少等优势，在求解实际优化问题时具有较高的效率。然而，RSO与其他算法相似，在求解复杂的高维实际约束性优化问题时，存在全局寻优精度低，早熟和搜索效率低等不足。

鉴于此，为提升RSO算法的性能，提出一种Sin混沌空翻反向学习鼠群优化(SSRSO)算法，用于求解复杂的约束优化问题。本文首先介绍了RSO算法；其次，在分析RSO算法的不足基础上，介绍了SSRSO算法，该算法在搏斗行为中引入空翻反向学习策略对种群进行反向学习，提高算法的全局寻优能力；采用Sin混沌映射与空翻反向学习初始化策略对算法初始种群初始化，保证算法的初始寻优性能；并引入非线性跳跃波动衰减因子A和C，协调算法的全局与局部搜索能力。最后，通过不同的测试函数和复杂环境下的移动机器人路径规划仿真实验验证了所提出SSRSO算法的寻优能力与实际应用有效性。

1 鼠群优化算法(RSO)

RSO算法主要通过模拟老鼠群体为获取丰富的猎物，与猎物之间进行追逐和搏斗的行为。为更好地模拟这两种行为，可建立如下的数学模型：

(1)追逐行为。当老鼠群体中最佳老鼠发现猎物时，其他的老鼠会根据当前的猎物位置，沿着最佳老鼠的位置不断地追逐猎物，从而实现不断地向猎物靠近，改变自身的位置。这种追逐猎物行为可简化为式(1)～式(3)来描述。

P=A×Pi(k)+C×(Pb(k)-Pi(k))

(1)

(2)

C=2×rand()

(3)

式中，Pb(k)为老鼠群体的当前最优位置；Pi(k)为老鼠群体的当前位置；a为[1,5]内的随机数；rand为[0,1]内的随机数；k为当前迭代次数；kmax为最大迭代次数。

(2)搏斗行为。当老鼠群体靠近猎物附近时，通过不断地移动自身位置，与猎物发生激烈的搏斗，从而实现围捕猎物的目的。这种老鼠群与猎物之间的搏斗行为可以简化为式(4)来描述。

Pi(k+1)=|Pb(k)-P|

(4)

式中，Pi(k+1)为第k+1次的老鼠群体的位置。

2 Sin混沌空翻反向学习鼠群优化算法(SSRSO)

2.1 空翻反向学习(SOBL)策略

标准的反向学习策略(opposition-based learning，OBL)[11]利用当前解的反向解择优选择替代当前解进行迭代寻优，这种机制可以增强算法种群的质量和多元性，在算法迭代初期搜索效果较好，但是，随着迭代次数的增加，产生的反向解可能会陷入局部极值附近，使得算法容易陷入局部最优，降低算法的收敛性能。针对反向学习机制存在的不足，受“空翻”竞技动作的启发，提出一种空翻反向学习策略(somersault opposition-based learning，SOBL)。

如图1所示，空翻是竞技运动(武术比赛、体操比赛等)中常见的动作之一[12]，运动员通过控制腾起角度β2(0<β2<π/2)可以获得不同的腾起高度H，然后可以不同的落入角度β1(0<β1<π/2)，落地到不同的位置，这样就可以实现位置的变化。在一维空间内，假设以运动员的腾起最高点的投影为基点O，x轴上解的搜索范围为[a,b]，y轴表示运动员腾起的最高高度位置，假设有一个运动员在x轴上的投影为x，通过空翻后的位置在x轴上的投影为x*。因此，运动员个体x产生的反向运动员个体为x*。在图1中，以O点为基准点，运动员个体x产生的相应的反向点x*，在三角形中可知：

(5)

(6)

由式(5)、式(6)可知：

(7)

x*=a+b-x

(8)

由此可知，式(8)为标准的反向学习策略。显然，标准反向学习策略为空翻反向学习策略的一种特例。采用空翻反向学习可通过改变落入角度β1和落入角度β2，可实现反向解的动态调整，进一步增强算法寻优精度。

将式(7)扩展到D维优化问题中，得到基于空翻反向学习策略的式(9)。

(9)

图1 空翻反向学习策略

在RSO中，随着迭代次数的增加，搜索空间中的种群的多样性不断地降低，容易使算法陷入局部最优。在搏斗行为中引入空翻反向学习策略，利用空翻反向学习策略产生当前的反向新解，如图2所示，通过“空翻”鼠群个体可以不断地产生新的解，这样就保证了在搜索空间内鼠群个体的多样性和质量，有利于提高算法的收敛效率和全局收敛精度。

图2 空翻反向搏斗学习策略

2.2 Sin混沌空翻反向学习初始化策略

Sin混沌映射[13]经常用于对算法的初始种群进行初始化，来增强种群的初始均匀分布性，保证算法初始寻优精度与效率。因此，将Sin混沌映射与空翻反向学习结合，对种群进行初始化，有利于算法找到最优初始解。Sin混沌映射如式(10)所示。

(10)

式中，xn为[-1,1]内的初始序列值，且不为0。由Sin混沌映射产生的种群x={xi,i=1,2,…,N}，xj={xj,j=1,2,…,D}，种群个体可以由式(11)表示。

xi+1,j=sin(2/xi,j)

(11)

式中，xi+1,j为第i+1个种群在j维上的值。

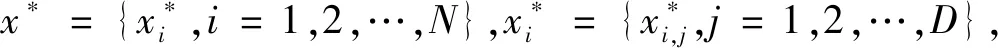
(12)

式中，[xmin,xmax]为搜索空间的动态边界，将种群x和x*进行合并，对新种群进行适应度大小排序，选择前N个最优的种群个体作为算法的初始种群。

2.3 非线性跳跃衰减波动因子

在RSO中，参数A与C共同控制着算法的全局搜索与局部开发的能力。但是，参数A呈现线性递减变化，自身缺乏动态波动可调性，同时参数C是一个[0,2]内的随机数，随机性与盲目性较大。参数A和C原有的控制方式，一方面不利于，算法的局部搜索开发的多元性，增加陷入局部极值的可能性，另一方面，对于全局搜索空间的扩大波动性较弱，造成全局勘探能力低下，易降低算法的搜索精度。为改善这个问题，引入“跳跃机制”对参数A和C采用具有非线性跳跃衰减波动因子如图3和图4所示。也就是分别将式(2)、式(3)修改为式(13)、式(14)。

(13)

式中，b=5；d=3；f=2。

(14)

式中，c=2。

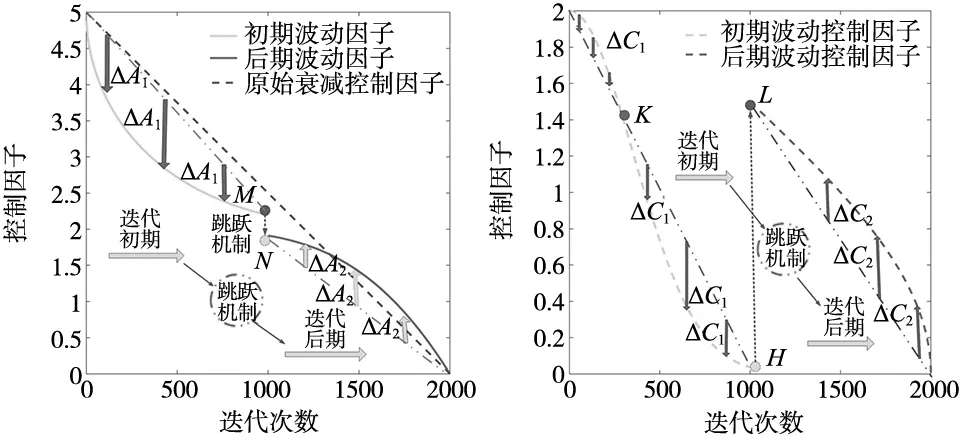
图3 非线性跳跃衰减波动因子A 图4 非线性跳跃衰减波动因子C

由图3可知，在迭代初期，参数A呈现出非线性递减，且波动幅度ΔA1先增大后减小，通过“跳跃机制”，在迭代中期，参数A由点M突然跳跃下降至点N转入迭代后期，在迭代后期，参数A仍呈现出非线性递减，且波动幅度ΔA2<ΔA1且先增后减。

由图4可知，在迭代初期，参数C呈现非线性递减，波动幅度ΔC1先增后减，在K点之前，波动幅度ΔC1较小，K点之后，波动幅度ΔC1较大。在迭代中期，参数C由点H突然跳跃增至点L，且跳跃幅度ΔHL大于参数A的跳跃幅度ΔMN，在迭代后期，参数C仍呈现出非线性递减，且波动幅度ΔC2>ΔC1且先增后减。通过采用这种非线性跳跃衰减波动因子策略，利用非线性衰减特性，可以增加算法搜索效率，加快算法的收敛速度；波动的变化方式有利于扩大算法搜索空间，增强算法的全局搜索能力，同时利用“跳跃机制”的升降突变特性，进一步有利于增强算法的局部搜索能力，平衡算法的全局搜索和局部搜索，提高算法的寻优性能。

2.4 SSRSO算法流程及步骤

Sin混沌空翻反向学习鼠群优化算法(SSRSO)流程如图5所示，步骤如下：

步骤1：设置算法参数即种群数量N，问题维度D和最大迭代次数kmax；

步骤2：对SSRSO算法的初始种群采用Sin混沌空翻反向学习初始化，如式(10)～式(12)所示；

步骤3：评估适应度值确定初始最优种群和最优适应度值；

步骤4：更新非线性跳跃波动因子A和C；

步骤5：根据式(1)进行鼠群追逐行为更新鼠群位置；

步骤6：根据式(4)进行鼠群搏斗行为更新鼠群位置，并按照式(9)对当前鼠群位置进行空翻反向学习；

步骤7：重新评估适应度值并更新最优鼠群位置；

步骤8：判断是否满足最大迭代次数，若是，则输出全局最佳鼠群位置和最优适应度值，反之，返回步骤4继续寻优；

步骤9：算法寻优结束，输出最优结果。

图5 SSRSO算法流程图

3 实验仿真与分析

3.1 SSRSO算法寻优性能评估

为更好地验证SSRSO的寻优性能，选取RSO[9]，MFO[5]，GWO[4]，SCA[3]和SSRSO算法，同时选择不同的类型的6个测试函数如表1所示。

表1 测试函数

设置所有算法的运行计算次数为30次，最大迭代次数为500，种群数量大小为30。以平均值，标准差和收敛曲线来评价各算法的寻优能力。测试函数实验结果和收敛曲线分别如表2和图6所示。

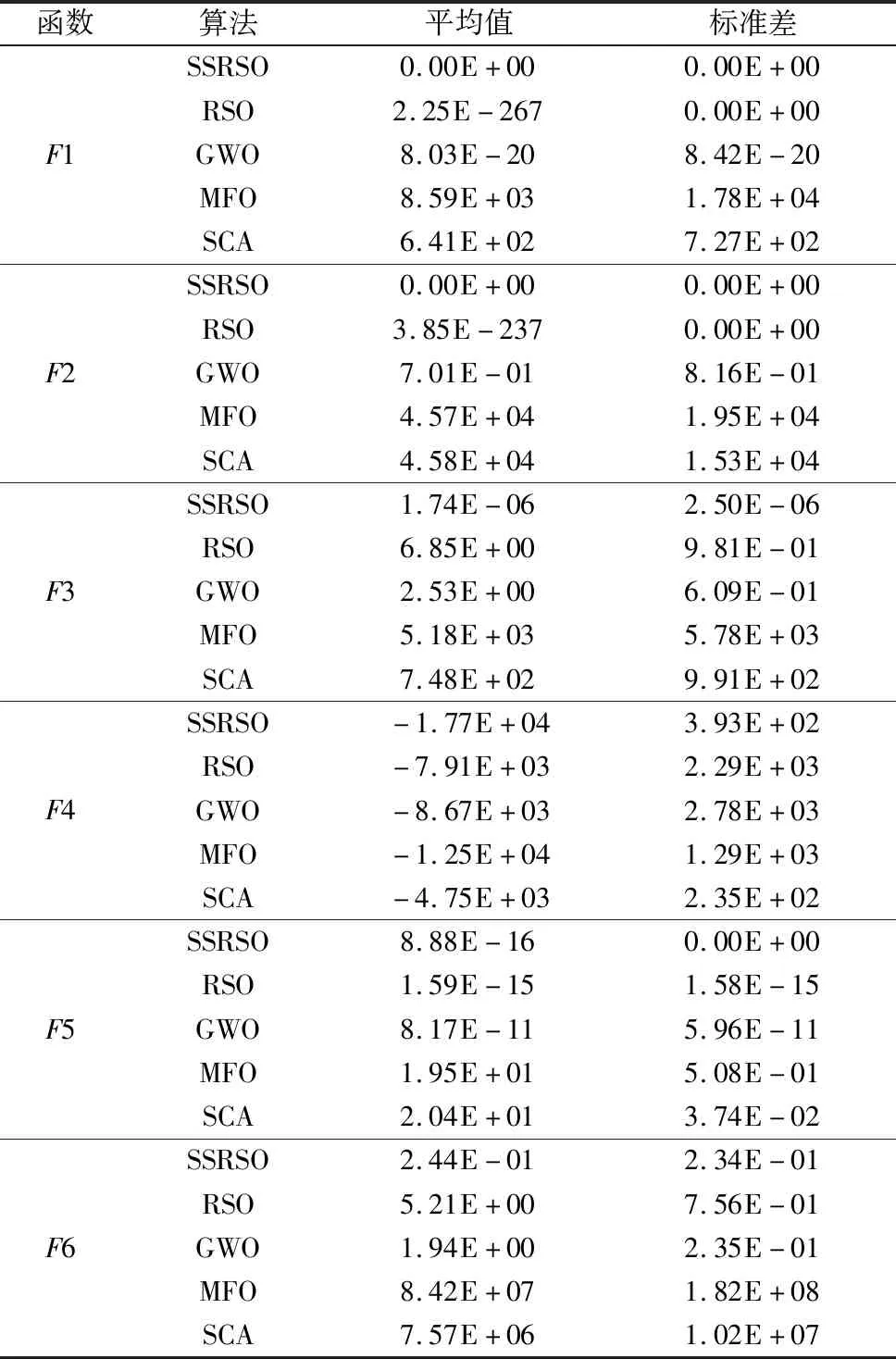
表2 测试函数实验结果

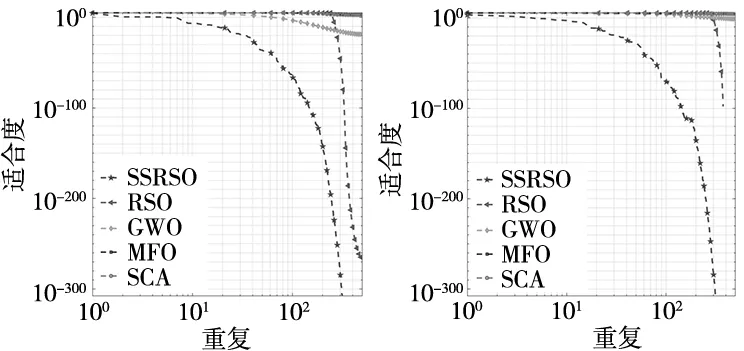
(a) F1 (b) F2

由表2中的平均值结果可知，相比RSO，GWO，MFO和SCA算法，对于所有测试函数，SSRSO算法可获得最小的平均值且优于其他算法。对于函数F1和F2，SSRSO算法均获得了全局最优解0。相比其他算法，对于单峰测试函数，SSRSO算法获得平均值精度至少提升了1E+06数量级。而对于多峰测试函数，SSRSO算法的平均值收敛精度至少提升了1E+01数量级。由此可见，SSRSO算法的寻优能力更优。由表2中的标准差结果可知，对函数F1，F2和F5，SSRSO算法的标准差为0优于RSO，GWO，MFO和SCA。对函数F4，SSRSO算法的标准差优于RSO，GWO和SCA，次于SCA算法，但其平均值优于SCA算法。对函数F3和F6，SSRSO算法可获得较小的标准差优于其他算法。因此，SSRSO算法的稳定性和局部探索能力优于其他算法。综上可知，SSRSO算法的寻优性能得到了较大的改善。这是由于控制参数具有“跳跃”和波动特性，平衡了全局与局部之间的转换能力，进一步采用新颖的空翻反向学习机制和Sin混沌映射增强了算法的种群多样性和质量，算法的收敛效率和精度得以进一步提升。

由图6可知，相比RSO，GWO，MFO和SCA算法，SSRSO算法的收敛效率和精度明显优于其他算法。从收敛曲线来看，RSO算法在迭代初期收敛速度缓慢，局部寻优能力较弱。但SSRSO算法在迭代初期可以快速的下降，收敛速度明显提升，这是采用Sin混沌空翻反向学习策略，保证了算法初期种群的多元性与质量，提升算法迭代初期的收敛效率与精度。从迭代过程中，SSRSO算法收敛曲线具有突降趋势(如图6d和图6e所示)，这是采用“跳跃机制”波动非线性因子，增强了算法的全局勘探与局部探索之间的平衡能力。因此，相比其他算法，融了多种策略的SSRSO算法寻优能力更加优越，具有较好的稳定性与鲁棒性。

3.2 移动机器人路径规划实验

将SSRSO算法应用于求解移动机器人路径规划问题来验证其实际应用的有效性。采用栅格法建立两种不同的规格地图环境(15 m×15 m和45 m×45 m)分别如图7、图8所示。该问题可以简化为躲避障碍物(黑色方块)条件下，由开始位置通过可移动的区域(白色方块)移动到结束位置时，移动机器人走过的最短路径长度。在相同环境下，设置种群数量为100，最短迭代次数为500。选用RSO，GWO，SCA，MFO和SSRSO分别求解20次，路径规划结果如表3所示。

图7 15 m×15 m地图 图8 45 m×45 m地图

表3 不同规格地图机器人路径规划对比结果

由表3结果可知，对15 m×15 m和45 m×45 m地图，SSRSO算法的最小路径长度分别为22.206 m和65.263 m。SSRSO算法所获得的平均路径长度分别为22.247 m和67.344 m。对不同的地图规格，SSRSO算法的最小路径长度和平均路径长度均短于RSO，GWO，MFO和SCA算法。同时，SSRSO算法拥有最小的标准差。由表3成功率和平均耗时可知，RSO和GWO算法成功率均未到达100%，而SSRSO，SCA和MFO算法均可以100%的成功率求解移动机器人的路径规划问题。这也说明了SSRSO算法的稳定性和鲁棒性更好。SSRSO的平均耗时均长于其他算法，RSO算法耗时最短，GWO，MFO和SCA算法耗时居中。地图环境越复杂，SSRSO，GWO，RSO，SCA和MFO算法的耗时均增加，但增幅不大。

对于15 m×15 m和45 m×45 m地图环境，与RSO，GWO，MFO和SCA算法相比，由图9、图10可看出，SSRSO算法路径规划更合理，最短路径规划线路折弯次数较少和平滑度较好，最短路径长度短于其他方法。

图9 15 m×15 m最小路径规划 图10 15 m×15 m最小路径收敛曲线

由图11、图12的迭代收敛曲线可知，SSRSO算法最短路径收敛曲线均位于RSO，GWO，MFO和SCA算法的下方，SSRSO算法的收敛下降更快，可快速的寻得最短路径长度。在迭代初期阶段，RSO算法收敛曲线较平直，说明难以跳出局部极值，然而，SSRSO算法可以改善这种现象。

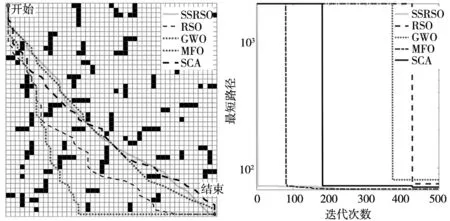
图11 45 m×45 m最小路径规划 图12 45 m×45 m最小路径收敛曲线

由以上结果可知，针对复杂的移动机器人路径规划问题，与其他算法相比，SSRSO算法均可提供有竞争的路径规划结果，一方面表明了它具有很强的实际应用性，另一方面，融合了空翻反向学习，“跳跃”非线性波动机制和Sin混沌映射机制增强了SSRSO算法求解实际问题的稳定性与鲁棒性。

4 结论

为提高RSO算法求解移动机器人路径规划问题的求解精度与效率，提出一种Sin混沌空翻反向学习鼠群优化(SSRSO)算法，结论如下：

(1)受“空翻”动作的启发，提出一种新颖的空翻反向学习策略，可明显地改善算法陷入局部停滞的现象，增强算法的寻优能力。

(2)引入“跳跃”非线性波动机制，在SSRSO算法追逐行为中嵌入非线性跳跃波动因子，增强了算法全局与局部之间的动态转换能力；种群采用Sin混沌空翻反向学习初始化，增强了算法的初期收敛效率和精度；同时对种群进行空翻反向学习，提高算法全局寻优能力。

(3)测试函数与移动机器人路径规划实验结果表明：与RSO，GWO，MFO和SCA算法相比，SSRSO算法的寻优性能优于其他算法，能够有效的躲避障碍物，路径规划结果优于其他算法，求解精度更高和稳定性更强，具有较好的实际应用性。