基于双谱分析的高原灌木回波信号分类
2022-11-09李立元栗苹李国林张广为
李立元 栗苹 李国林 张广为
(北京理工大学 机电动态控制重点实验室, 北京 100081)
近年来,在各代干扰机、微波武器、大功率信号等一系列的干扰下,无线电引信极有可能因此出现早炸或失效的情况。 太赫兹波的工作频率避开了高功率微波武器、雷达、干扰机等常用的工作频段,再加上太赫兹波在大气中的衰减较大[1-2],主要适用于近程探测,因此太赫兹波应用于引信之上具有天然的优势[3]。
对地的无线电引信获得的回波能量取决于地面散射系数,而地面散射系数又取决于地面类型、落角等一系列因素[4-5]。 面对不同类型的地面,回波能量具有极大的差异。 而在很长一部分中国边境线的高原上,由于空气的稀薄,同样对回波能量的大小造成了影响。 综上所述,获取太赫兹信号在高原不同地貌下的回波特性,并实现对回波数据快速分类从而确定炸高,对于保证引信的毁伤效能显得尤为重要。
因此,实地采集了高原各种地貌下的回波数据,本文仅仅对灌木地形下的回波双谱用4 种积分双谱进行降维与分类,从而在占用很少资源的情况下实现对引信炸高的识别。
1 双谱的基本理论
1.1 双谱的定义
高阶谱是通过累积量函数(cum)来定义的,因此也被称作累积量谱。 假如是一个零均值的k阶平稳过程,则将该过程的k阶累积量定义为

式中:ω为傅里叶变换到频域得到的频率分量;功率谱、双谱(三阶谱)、三谱(四阶谱)分别为k=2,3,4 时的特殊情况。
本文所用双谱(三阶累积量谱)为
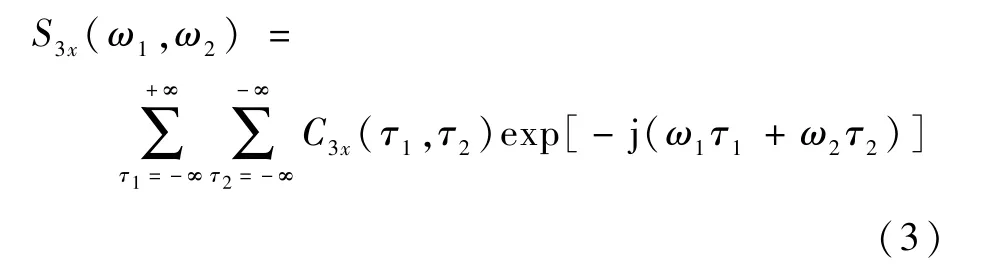
1.2 积分双谱
双谱是二维函数,可以直接通过卷积神经网络(CNN)等方式直接进行分类,但由于数据计算量过于庞大,严重限制了双谱在引信上的应用。因此,可以按照一定的规则对双谱值进行积分,将二维函数转化为一维函数[6],从而大大减少分类时的难度及计算量,通过双谱的对称性,计算量则会进一步减少。 根据选定的积分路径,将积分双谱分为以下4 种[7]。
1.2.1 径向积分双谱
如图1 所示,在双谱平面上,积分路径取过原点的直线,得到的积分值即为径向积分双谱(radially integrated bispectrum, RIB)。
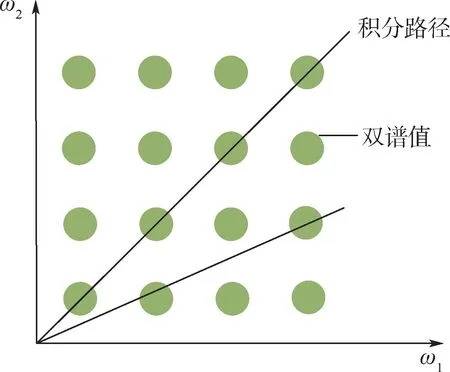
图1 径向积分双谱Fig.1 Radially integrated bispectrum
RIB 具有一个明显的缺陷:如果斜率的步长选择过大,那即使积分路径上的所有ω2均取整,仍然会有点被遗漏,而这些点可能包含重要的信息。 如果斜率的步长选择过小,路径上取整后的ω2必然还会有所重复,从而造成一些双谱值被重复积分,从而导致双谱积分值特征不明显。
1.2.2 轴向积分双谱
如图2 所示,在双谱平面上,积分路径取平行于ω1轴或平行于ω2轴的直线,得到的积分值即为轴向积分双谱(axially integrated bispectrum,AIB)。AIB 使用了每一个双谱值并确保双谱值不会被重复使用,但其丢失了绝大部分相位信息。
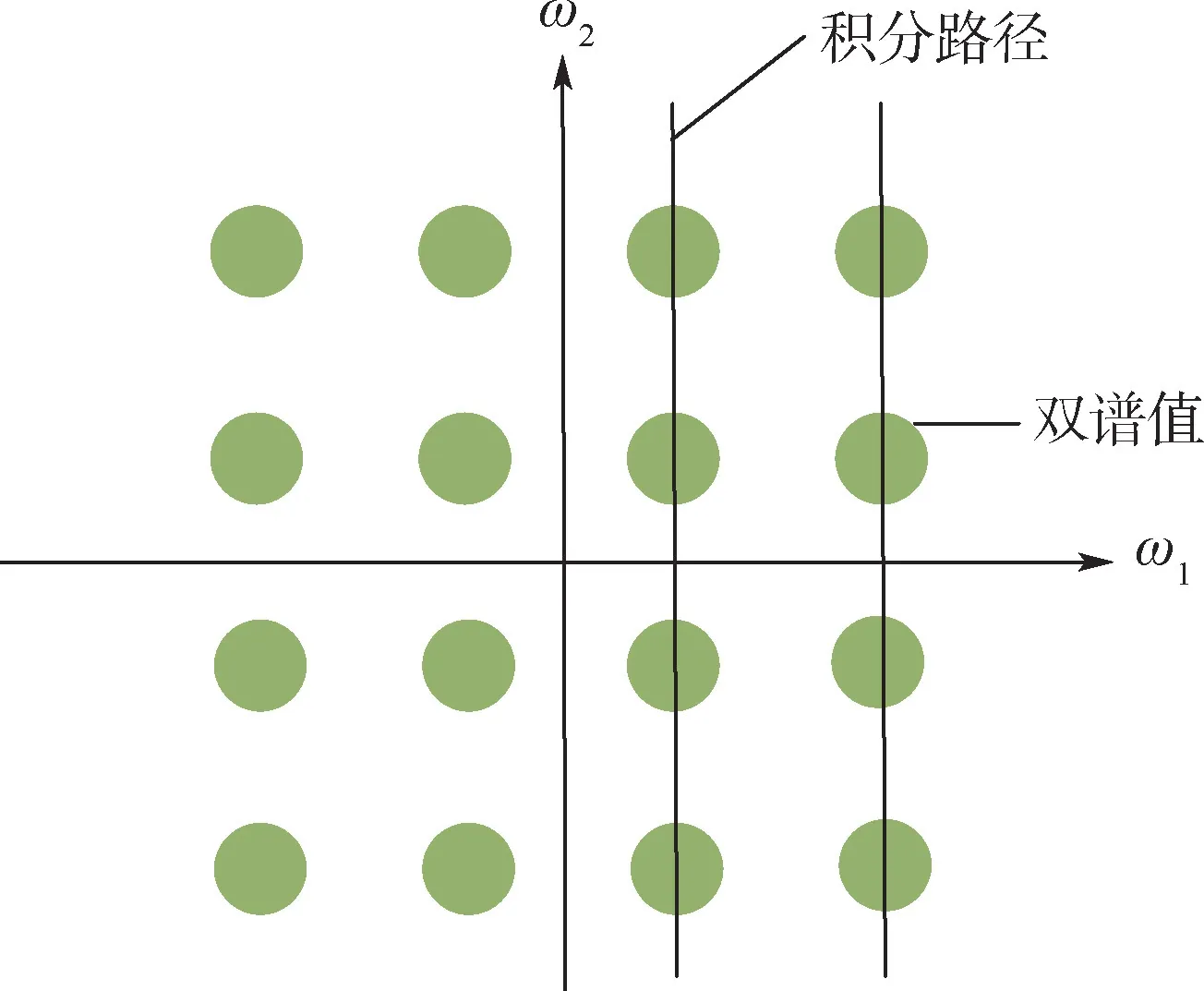
图2 轴向积分双谱Fig.2 Axially integrated bispectrum
1.2.3 圆周积分双谱
如图3 所示,在双谱平面上,积分路径取以原点为圆心的圆周,得到的积分值即为圆周积分双谱(circularly integrated bispectrum, CIB)。
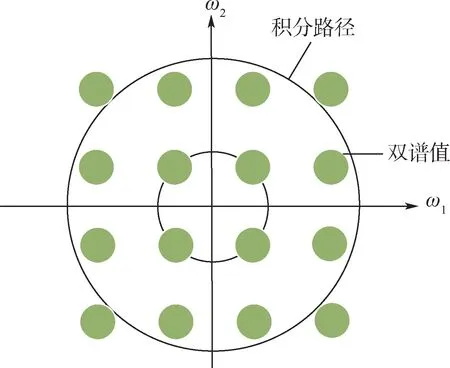
图3 圆周积分双谱Fig.3 Circularly integrated bispectrum
同样的,由于步长的原因,CIB 在积分时必定会遗漏一部分双谱值。
1.2.4 围线积分双谱
如图4 所示,在双谱平面上,积分路径取以原点为中心的正方形,得到的积分值即为围线积分双谱(surrounding-line integral bispectrum, SIB)。SIB 同样使用了每一个双谱值并确保双谱值不会被重复使用,同时保留了信号的尺度信息及部分相位信息[8-9]。

图4 围线积分双谱Fig.4 Surrounding-line integral bispectrum
2 实验数据处理
2.1 信号模型
2.1.1 目标亮点模型
如图5(a)所示,以地面为目标时,高原上地面粗糙,检测出的回波信号必然是多个目标回波信号的叠加,因此可能导致无法识别出正确的炸高。 图5(b)为实采数据频谱,通过图像可以明显看出,频率值具有多个峰值,说明检测到了不同距离目标的回波信号。

图5 多目标回波示意图Fig.5 Schematic diagram of multi-target echo
大部分无线电引信以地面分布的对象作为目标,为了准确地探测地面目标,必须建立一个有效的回波信号模型。
目标回波是目标对于信号源发射的信号做出的一种响应,目标的固有散射特性和发射电磁波都会对回波信号造成影响[10]。 回波特性与入射的初始时间无关,因此可以将目标看做一个线性时不变系统,回波就是对入射波的响应。 可以将单个目标的传递函数Hn(ω)定义为
Hn(ω)=An(ω)exp(iωτ+ iϕ) (4)
式中:An(ω)为幅度反射系数,是关于频率的函数;τ为时延,是关于目标反射距离的函数,τ=2R/c,R为参考点到信号源的波程,c为光速;ϕ为回波产生的相位差。
因此,函数可以视为一个多亮点叠加的模型,总的传递函数表示为
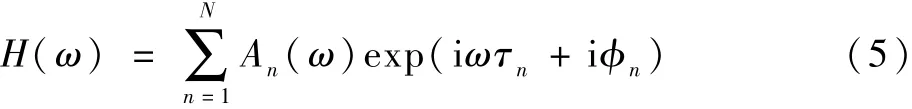
2.1.2 信号仿真
如图6 所示,通过在Simulink 模型中添加2 个不同的距离,从而得到双亮点接收信号的数字特征。 模型中默认幅度反射系数为相同值。

图6 双亮点回波Simulink 模型Fig.6 Simulink model of double bright spot echo
如图7 所示,能很明显看出目标亮点模型的仿真结果与图5(b)中的实采信号包络具有极高的相似度,一定程度上模拟出了地面目标的信号特征,之后还可以通过添加地杂波进行进一步研究。

图7 双目标亮点模型仿真结果Fig.7 Simulation results of double-target highlight model
2.2 数据采集平台
如图8 所示,将前端通过云台绑定在标志杆上,通过改变标志杆的高度h及发射信号与地面的夹角,从而获取不同的回波信号。 在本次实验中,高度h分别取2 m、3 m、4 m、5 m,发射信号与地面的夹角θ分别取20°、45°、65°、85°。
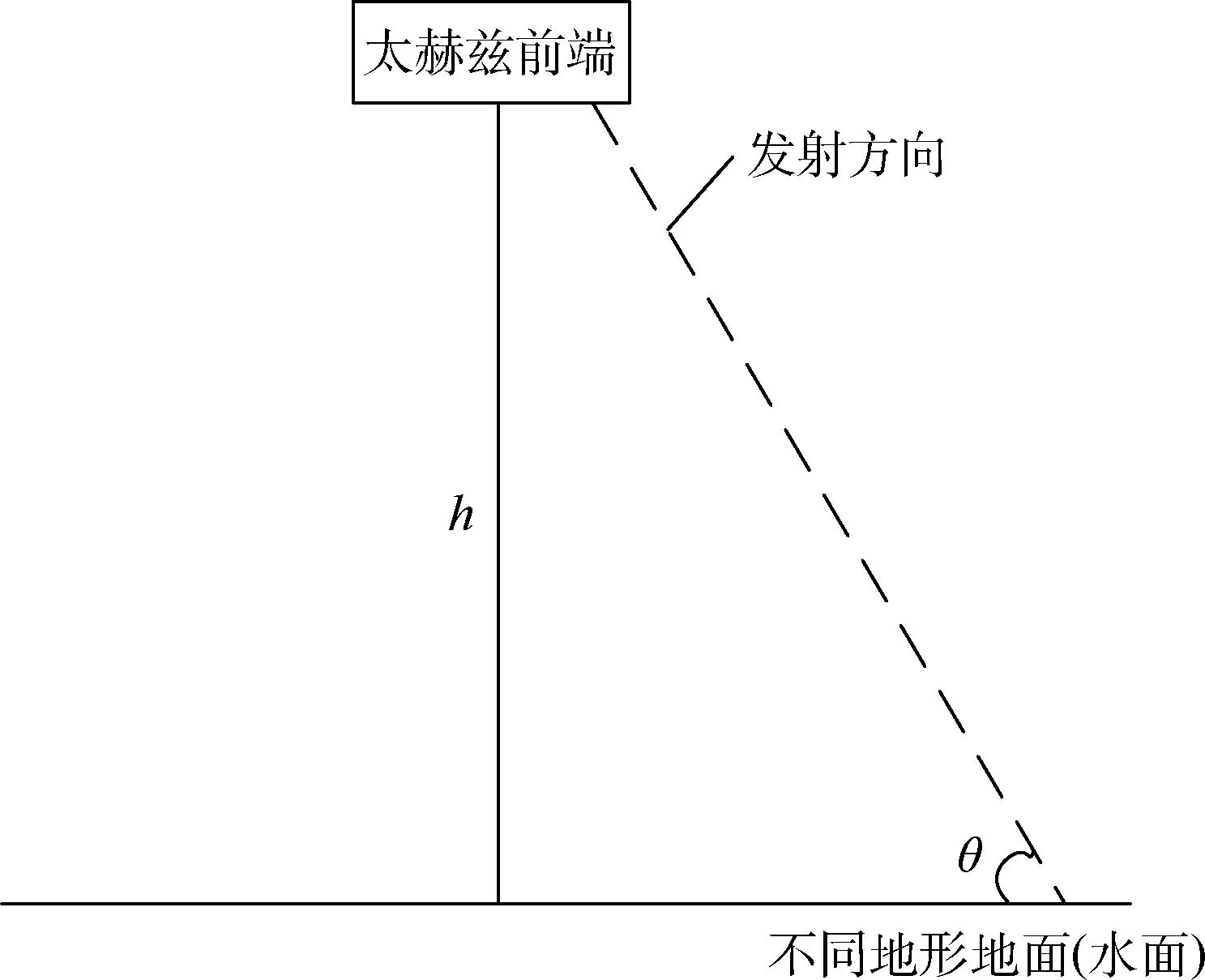
图8 数据采集平台Fig.8 Data collection platform
2.3 基于Hilbert-Huang 变换的优化信号双谱
2.3.1 经验模态分解
经验模态分解(empirical mode decomposition,EMD)是Hilbert-Huang 变换(HHT)最重要的步骤,HHT 利用EMD,得到信号各阶的本征模态函数(intrinsic mode function,IMF)。EMD 过程:首先,对原始信号进行处理,求出各个局部极大值点。 然后,用插值法连接这些点组成上包络线,同样找到极小值点连接这些点组成下包络线,用原始信号减去包络线均值就得到了第一个residue,如果其不满足IMF 定义(极值点和过零点数目至多相差一个,且包络线均值为0),就以该residue 作为原始信号继续重复上面的操作,直到得到第一阶IMF。 最后,用原始信号减去该IMF,得到新的信号,作为初始信号再重复上面的筛选过程,直到所得到的剩余部分为单一信号或其值小于设定值时,分解完成。
2.3.2 数据分解
将回波数据通过EMD 得到数据的各阶IMF及残余分量,对各阶本征模态函数进一步提取各种双谱特征用于验证分类的准确性。
图9 和图10 为初始信号及各阶IMF 示意图,其中采样频率为1 MHz,即采样时间间隔为1 μs。 图10 中纵坐标无实际意义,仅为将各阶本征模态函数直观地表示在同一张图中的相对参考位置。
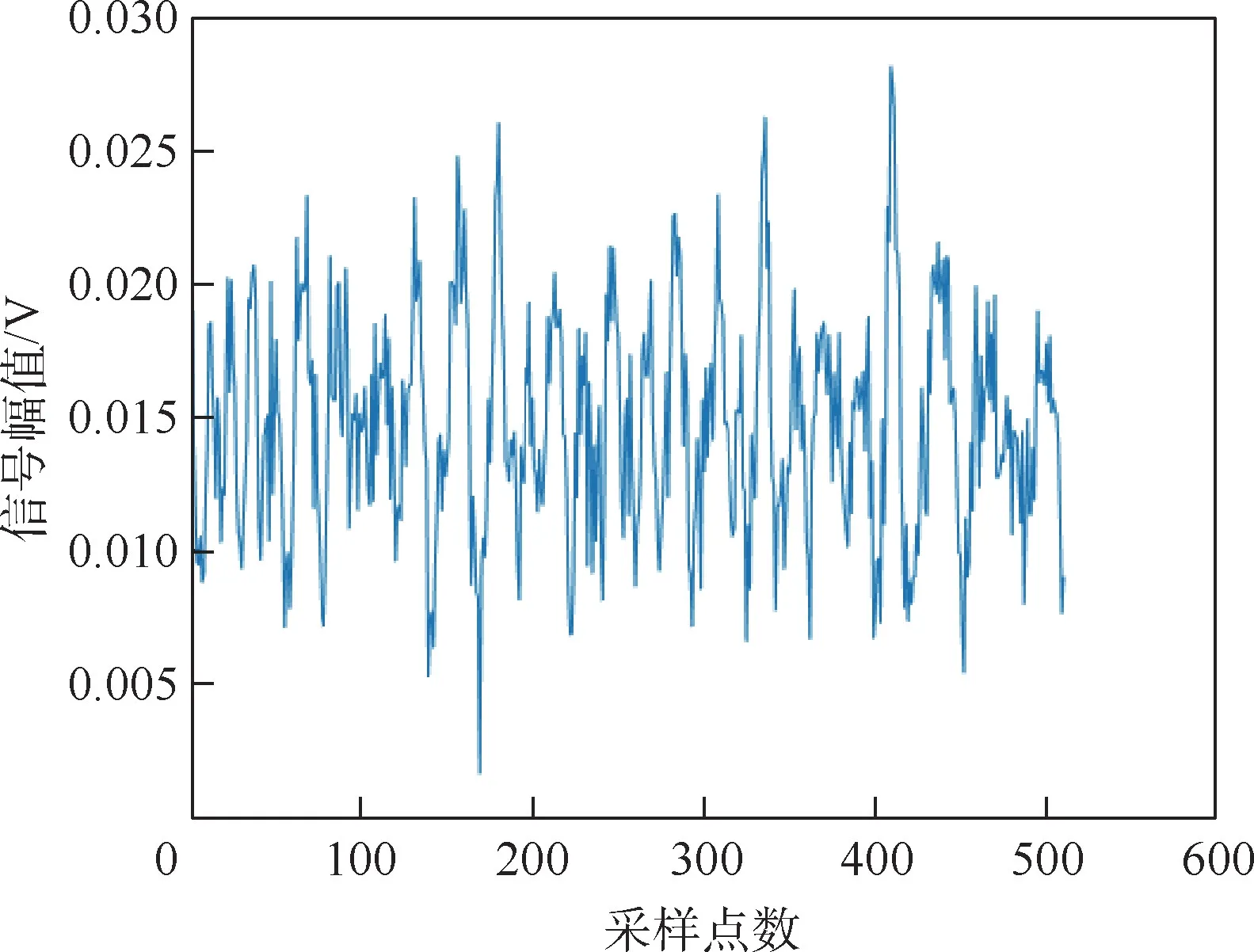
图9 初始信号Fig.9 Initial signal
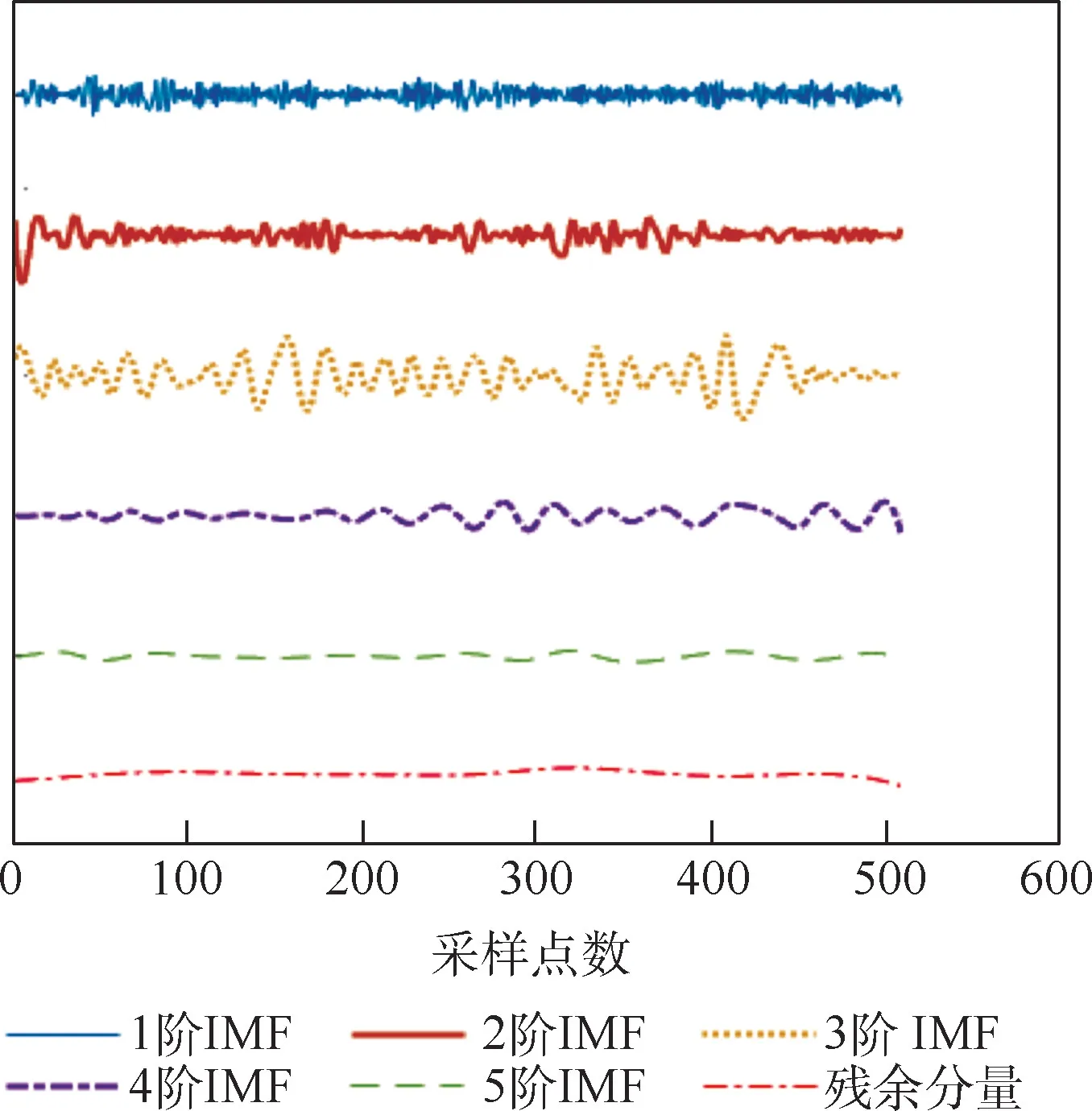
图10 各阶IMF 示意图Fig.10 Schematic diagram of IMF in each stage
为了更直观地看出IMF 信号瞬时频率的变化,每两阶提取一个IMF 信号的瞬时频率。 从图11可以明显看出,各阶IMF 分量的瞬时频率随着阶数的增加而降低,因此提取不同距离回波信号的同阶IMF 分量双谱特征,再次进行分类。 半数以上的当多次分类结果为同一结果时,结束对下一阶IMF 分量进行分类,否则持续此步骤,此时得到的信号为最终分类结果。 回波信号分类流程如图12所示。
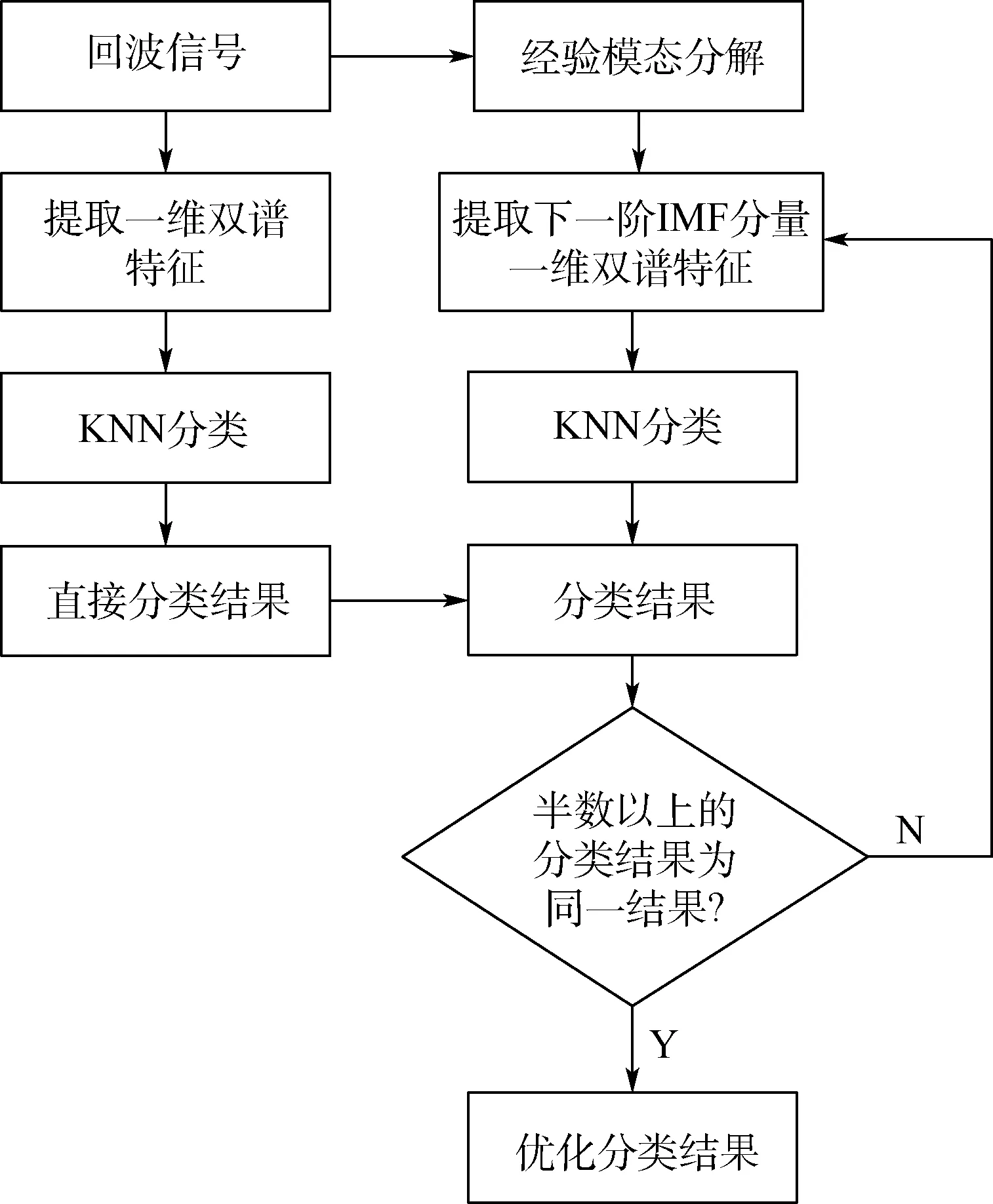
图12 回波信号分类流程Fig.12 Flow chart of echo signal classification
2.4 数据分析结果
2.4.1 灌木数据对比
在不同的高度上,回波信号具有不同的双谱特征,如图13 所示,分别为在θ=45°时距地面2,3,4,5 m 处的双谱分布。
如图13 所示,以f1、f2这2 个频率作为坐标轴来表示信号的偏斜程度在频域上的分解,分别得到在θ=45°时距地面,2,3,4,5 m 处的双谱分布。 可以明显地看出,2,3,4,5 m 处的双谱分布在幅值上具有明显的区别,但对于工作平台很小的引信来说,实时性是一个非常重要的指标,将二维数据转换为一维数据能够将数据量直接从x2(x为fft 次数)降为x,因此,科学有效地提取出一维双谱切片特征对于降低运算速度具有极大的帮助。

图13 θ =45°时不同高度双谱分布Fig.13 Bispectrum distribution at different heights at θ =45°
2.4.2 四种积分双谱特征
以θ=45°时4 个不同高度的4 种积分双谱为例,得到的结果如图14 所示。
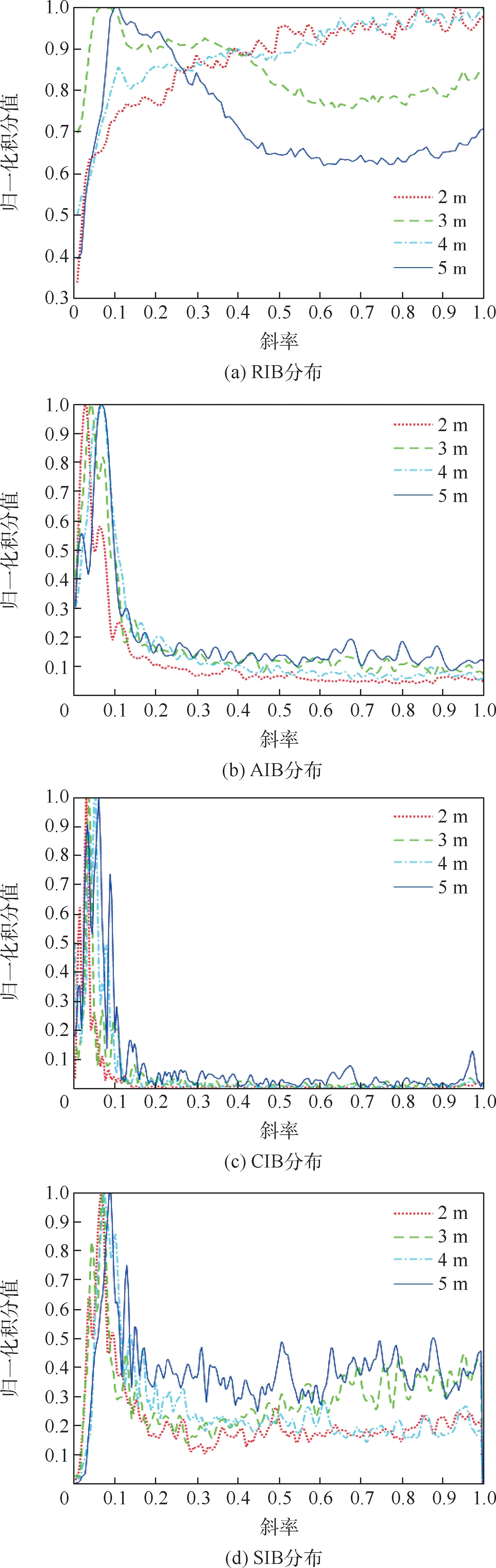
图14 θ =45°时不同积分双谱分布Fig.14 Bispectrum distribution by different integral bispectrum at θ =45°
从图14 中可以看出,将二维的双谱特征按照4 种方式进行积分并归一化之后,仍然具有显著的差异,保证了一维数据的分类处理仍具有很高的可行性。
3 数据分类
目前,主要采用的分类方法有概率神经网络(PNN)[11]、支持向量机(SVM)[12-13]、卷积神经网络(CNN)[14-15],由于最邻近节点算法(KNN)计算简便、计算速度快[16],符合引信实时性的要求,因此本文采用KNN 算法。
3.1 最邻近节点算法
最邻近节点算法也称为k最近邻算法,该方法简单且直观,如图15 所示。 每一个样本x通过计算到其他样本的距离,用与其最邻近的k个样本来进行分类,将样本x分为k个样本中数量最多的类别。 由于同样情况下回波信号的样本集重叠很多,用在本文非常合适。 该方法无需训练,适合应用于引信上。
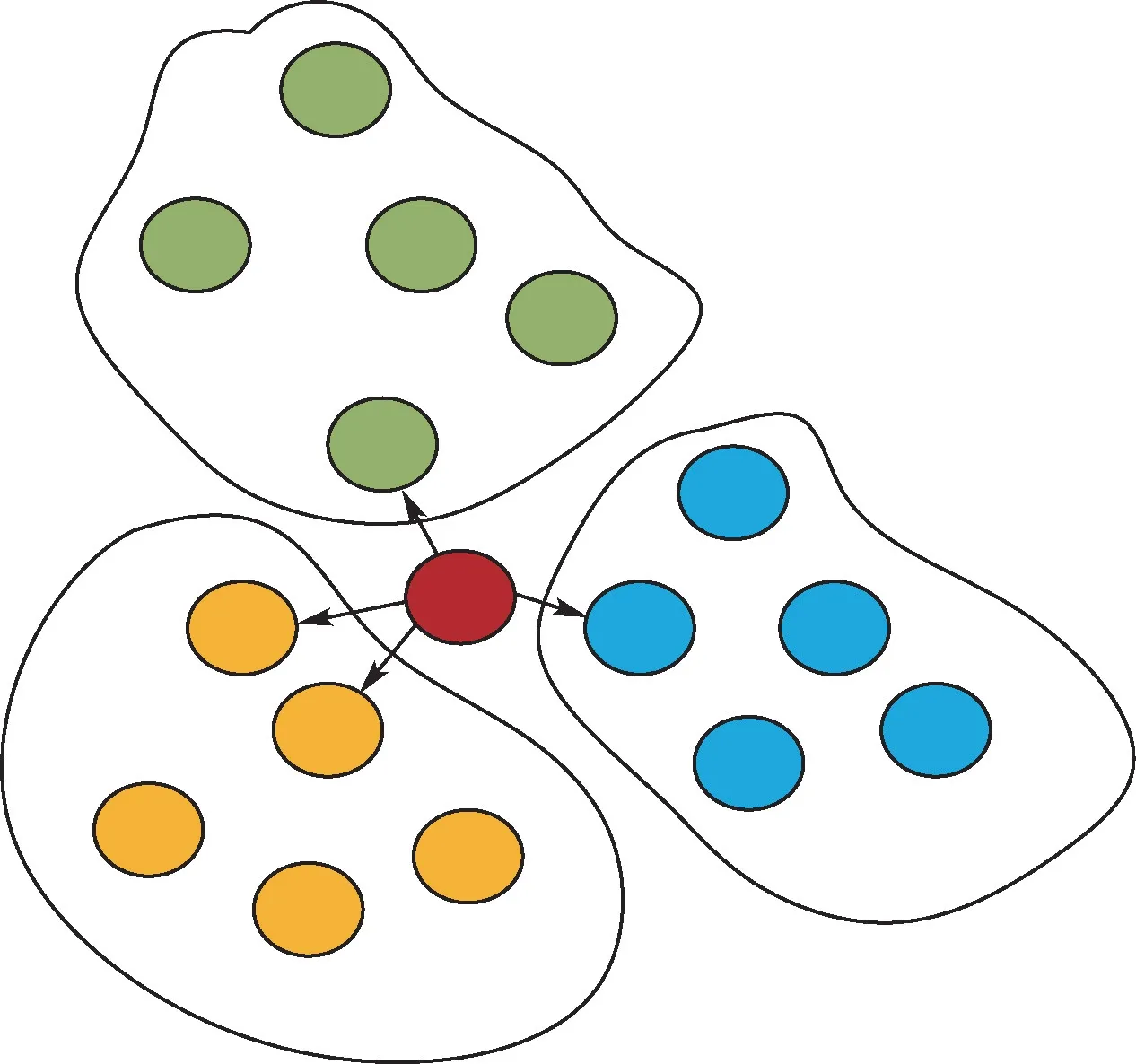
图15 最邻近节点算法Fig.15 KNN algorithm

3.2 实验数据分类
将4 种积分双谱得到的4 个高度、4 个角度的数据各取30 组,利用KNN 对其进行分类,得到结果如图16 ~图19 所示,黑色方框中的数据分别表示在对应数据下的分类正确的数量及所占分类数据总量的比例。
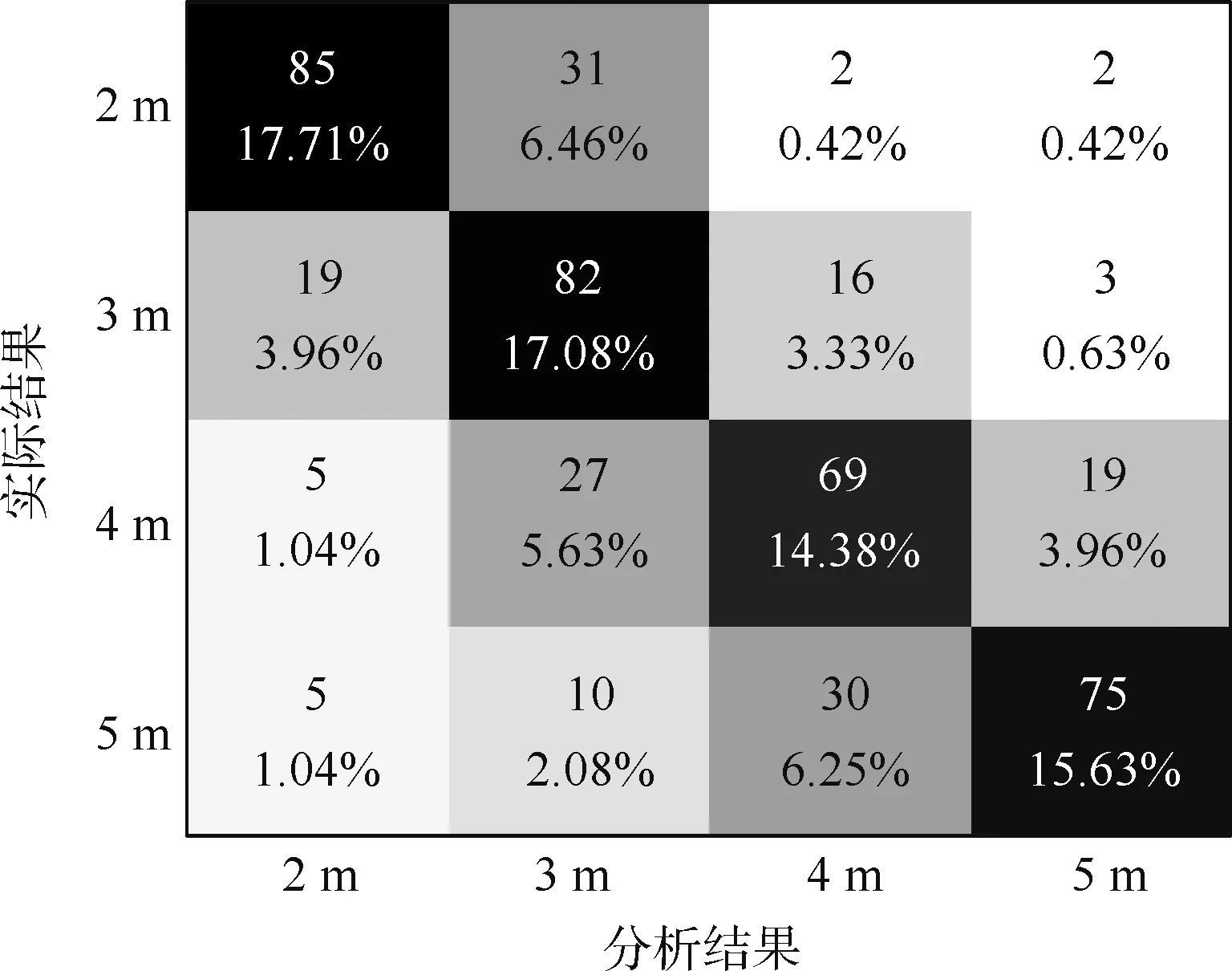
图16 RIB 分类结果Fig.16 RIB classification results
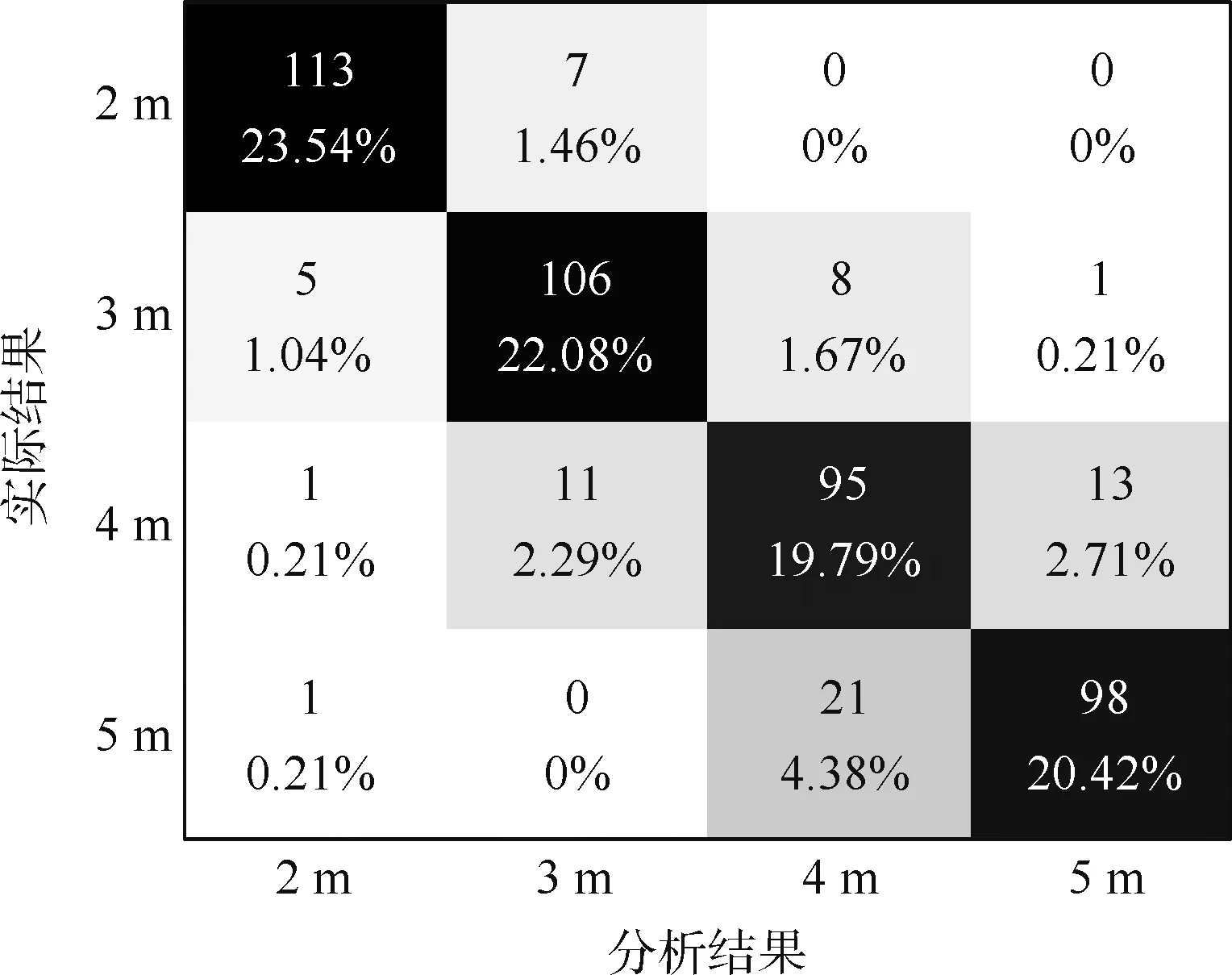
图17 AIB 分类结果Fig.17 AIB classification results

图18 CIB 分类结果Fig.18 CIB classification results
3.2.1 RIB 分类结果分析
对20°、45°、65°、85°这4 个角度120 组分类数据RIB 积分数据进行分类,最终可以得到4 次分类的准确率分别为61.7%、61.7%、69.2%、66.7%,利用RIB 对480 组数据分类的总准确率为64.8%。
3.2.2 AIB 分类结果分析
对20°、45°、65°、85°这4 个角度120 组分类数据AIB 积分数据进行分类,最终可以得到4 次分类的准确率分别为89.2%、91.7%、80.0%、82.5%,利用AIB 对480 组数据分类的总准确率为85.8%。
3.2.3 CIB 分类结果分析
对20°、45°、65°、85°这4 个角度120 组分类数据CIB 积分数据进行分类,最终可以得到4 次分类的准确率分别为84.2%、80.8%、80.0%、80.0%,利用CIB 对480 组数据分类的总准确率为81.3%。
3.2.4 SIB 分类结果分析
对20°、45°、65°、85°这4 个角度120 组分类数据SIB 积分数据进行分类,最终可以得到4 次分类的准确率分别为81. 7%、64. 2%、60. 0%、53.3%,利用SIB 对480 组数据分类的总准确率为64.8%。
3.3 分类结果比较
显然,利用KNN 对AIB 和CIB 得到的一维数据分类结果更为准确,准确率可以达到80% 以上,而对RIB 和SIB 得到的一维数据分类结果并不理想,分类的准确率只有65%左右。
通过表1、表2 可以看出,利用经EMD 对不同频率的数据进行特征提取后,分类结果有了明显的改进,成功率最多可提升约8.3%,分类总成功率提升3.7%。
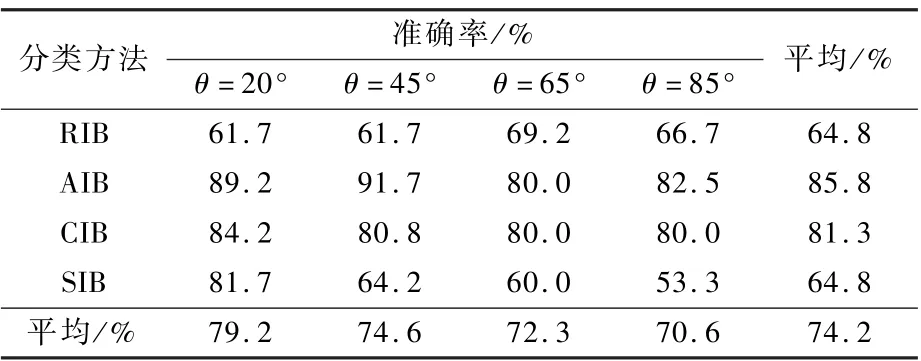
表1 分类结果汇总Table 1 Summary of classification results
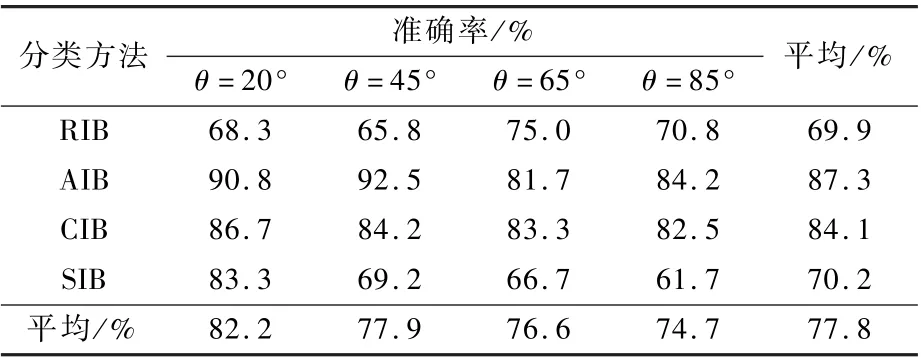
表2 优化双谱分类结果Table 2 Optimization of bispectral classification results
4 结 论
本文主要围绕双谱分析在信号处理中的应用,对实测高原地区灌木的回波进行了分析,通过4 种不同的积分双谱方式对双谱特征进行了降维,进而对一维特征进行了分类,分类结果表明:
1) 利用KNN 算法,得到了对2 m、3 m、4 m、5 m这4 个高度的分类成功率,最高可以达到74.1%。
2) 虽然在理论上SIB 算法利用了所有的点数和相位信息,但在实际数据分类中效果并不好。而AIB 与CIB 两种算法准确率较高,分别可以达到85.4% ~85.8%和81.5% ~81.3%,其中对于45°的数据,AIB 分类效果更为卓越,可以达到91.7%。
3) 利用EMD 对数据进行分解后,优化分类结果有了明显的提高,其中AIB 成功率最高可达92.5%。
4) 说明太赫兹波段的引信完全可以通过AIB 和CIB 两种算法实现快速准确的分类,利用HHT 优化的双谱数据对于提升分类识别结果的准确度具有一定的作用。
