基于阵列天线波束形成的卫星导航信号提纯

史鹏亮 王晓宇 薛瑞

(1. 北京航空航天大学 电子信息工程学院, 北京 100083;

2. 空军研究院, 北京 100085; 3. 中国电子科技集团公司第二十研究所 导航专业部, 西安 710072)

卫星导航系统具备覆盖范围广、定位精度高等优点,已被广泛应用于局部战争中的飞机、车辆和舰船导航,以及精确武器制导等军事应用领域[1]。 卫星导航欺骗技术通过发射虚假的卫星导航信号,引导目标接收机跟踪虚假信号从而得到错误的定位结果,因其易于实现、隐蔽性强和破坏性高而受到越来越多的关注[2-4]。 卫星导航欺骗技术分为生成式和转发式2 类[5-6]。生成式欺骗需要完全掌握卫星导航信号的伪码类型、加密方式和导航电文内容,因此难以应用于军用信号。 对于军事对抗,可行的方法是采用转发式欺骗方法,通过对接收到的军用卫星导航信号进行延时后转发给目标,使其错误定位到指定位置。

对于转发式欺骗技术,如果对接收到的所有卫星导航信号进行统一延时和转发,只能使目标接收机定位到转发天线的位置,无法满足将目标诱骗至指定地点的目的,因此必须能够从接收到的信号中逐一提取出每颗卫星的信号,分别加以一定的延时并转发给目标。 然而,现代的卫星导航系统均采用码分多址的信号体制,在授权码未知的条件下,无法通过码相关方法对接收到的军用信号进行区分和提取。 因此,通过一定手段从接收天线获取的卫星导航信号中提取出每颗卫星的纯净信号,是转发式欺骗的必要条件。

对卫星导航信号的提纯可以通过使用固定波束的抛物面天线[7]或数字波束阵列天线[8-9]实现。 对于抛物面天线,通过机械转动使接收波束主瓣对准目标卫星方向即可获得该卫星的纯净信号,但若要同时获取多颗卫星的信号,则需要多部抛物面天线同步工作,造价昂贵且效率低下。数字波束阵列天线通过复用阵列天线的接收信号数据并行施加不同的幅相权值,可以快速形成并行指向不同卫星的数字接收波束,从而同时获取每颗卫星的纯净信号,以支持转发式欺骗。

通过使用阵列天线对卫星信号进行提纯,需要数字接收波束在目标卫星方向上形成主瓣指向,同时在其他非目标卫星方向上形成较低的旁瓣或抑制零陷。 常规波束形成方法在所有波束形成方法中稳健性最强,但形成的旁瓣有限。 Olen和Compton[10]通过在旁瓣区域放置若干虚拟干扰源,运用自适应原理,采用迭代法调节干扰强度达到控制波束旁瓣的目的,但存在迭代步长难以选择、容易导致主瓣快速增宽等问题。 Capon[11]提出的最小方差无失真响应(MVDR)波束形成方法,可以使波束主瓣方向的信号无失真通过,且在强干扰入射方向形成零陷,但该方法在无干扰的白噪声环境中蜕化为常规波束形成方法。 鄢社峰等[12-13]运用二阶锥规划方法提出了兼顾波束旁瓣级、主瓣宽度和阵增益等指标的波束优化设计方法,但需要使用凸优化计算工具,计算复杂度较高,不易于工程实现。

本文在描述波束形成基本原理的基础上,介绍了MVDR 波束形成方法并分析了MVDR 的信号提纯度,提出了数据协方差矩阵加载重构的优化波束设计方法并通过仿真试验进行验证。

1 问题描述

1.1 波束形成基本原理

假设阵列天线由M个各向同性阵元组成,各阵元的三维坐标可表示为

一般地,假设天线视野内存在D颗导航卫星。 由于卫星到阵列天线的距离远大于天线各阵元间的距离,可以假设卫星发射的导航信号入射到天线不同阵元的方位角和仰角相同。 令每颗卫星信号入射到阵列天线的方位角和仰角分别为θ1,θ2,…,θD和φ1,φ2,…,φD。 从(θd,φd)方向入射到天线的第d颗卫星的信号波数向量为

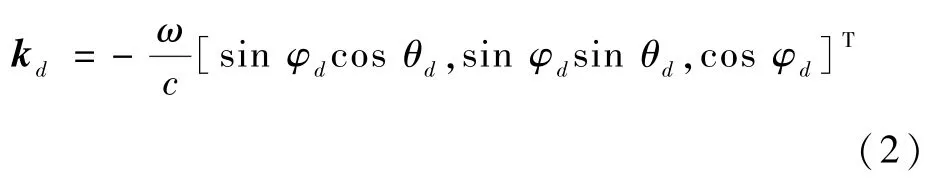
式中:ω=2πf为角频率,f为卫星导航信号载波频率;c=3 ×108m/s 为电磁波传播速度。

阵列天线在第d颗卫星信号入射方向上的阵列响应向量为

式中:sd(t)为第d颗卫星的信号;n(t)为系统电路中由带电粒子的热运动形成的热噪声。

基于波束形成的卫星导航信号提纯原理是对阵列天线的接收信号进行幅度和相位加权控制并合路输出,形成对某个卫星信号入射方向上的数字波束,从而通过空域滤波实现对该卫星信号的提纯,抑制干扰和环境噪声,提升接收信号的信噪比。 通过复用阵列天线的接收信号数据,并行对多颗导航卫星的信号进行空域滤波,可以同时输出多颗导航卫星的提纯信号。 基于波束形成的卫星导航信号提纯原理如图1 所示。

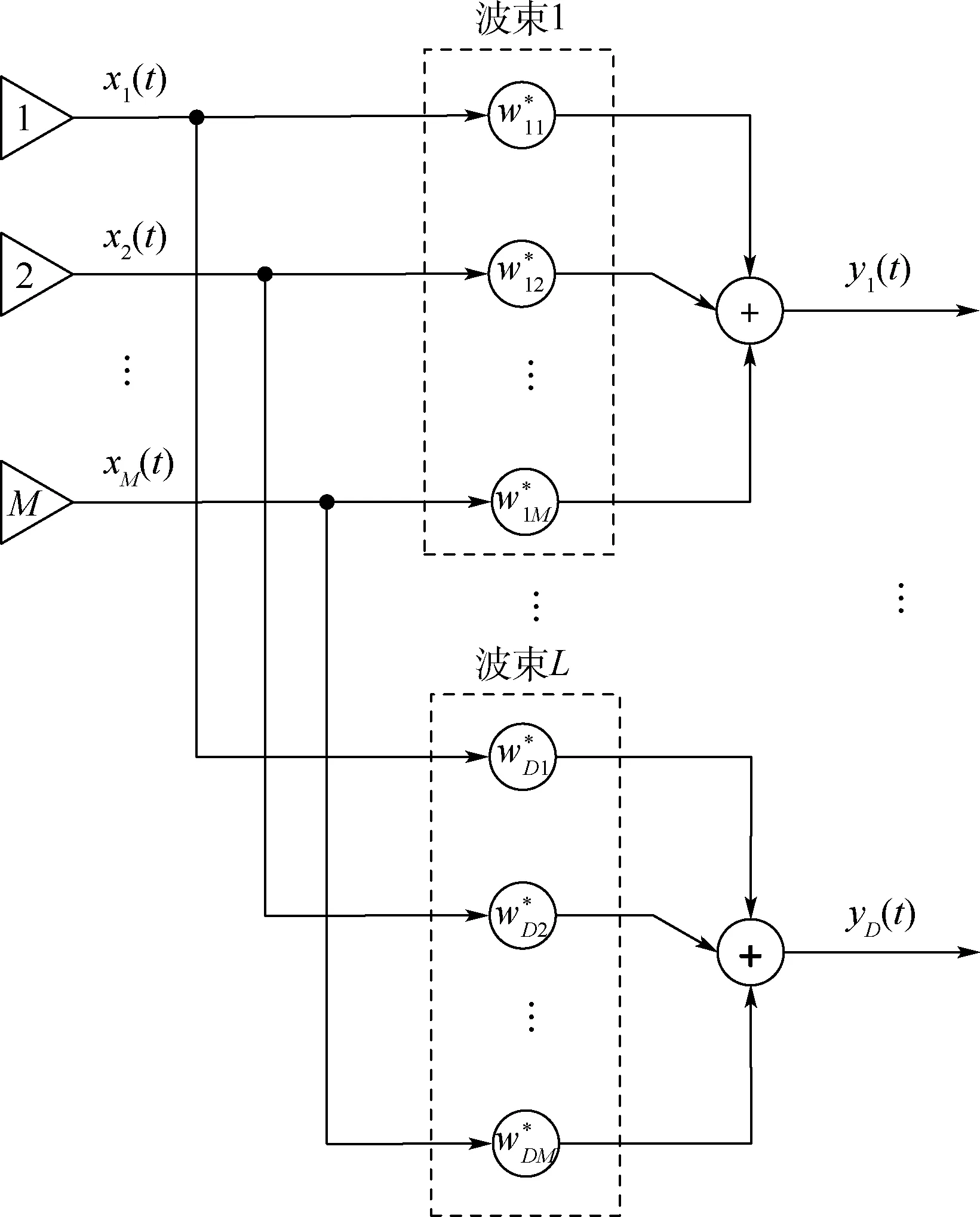
图1 基于波束形成的卫星导航信号提纯原理Fig.1 Principle of satellite navigation signal purification based on beamforming

对于第l(l=1,2,…,D)颗卫星信号提纯的波束形成器输出可以表示为

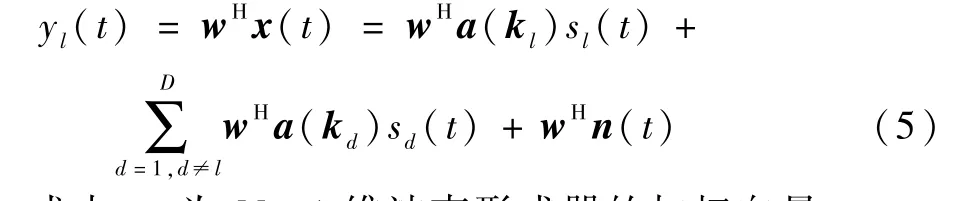
式中:w为M×1 维波束形成器的加权向量。

从式(5)可以看出,波束形成的目的是使等号右边第1 项的目标卫星信号成分无失真通过并获得阵列增益,使第2 项其他非目标卫星信号成分和第3 项噪声成分受到抑制。

1.2 信号提纯度

对式(5)表示的第l(l=1,2,…,D)个波束形成器输出信号,定义其中目标卫星信号分量和最大非目标卫星信号分量的功率比分贝值作为对卫星导航信号提纯度的衡量,描述如下:

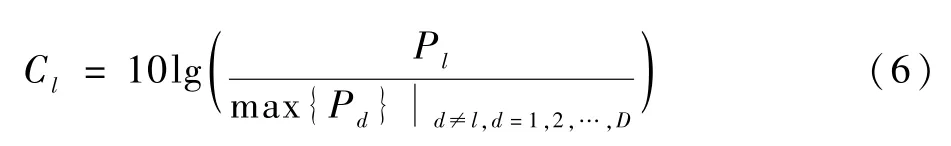
式中:Pl为输出信号中目标卫星信号的功率;Pd(d≠l,d=1,2,…,D)为输出信号中非目标卫星信号的功率。

为了避免接收机将与阵列天线输出信号中的非目标卫星信号的互相关峰误认为是与目标卫星信号的自相关峰。 提纯后波束形成器输出信号中的非目标卫星信号成分与接收机本地生成的伪随机码形成的自相关主峰值要小于或等于目标卫星信号成分与接收机本地码形成自相关最大侧峰值。 以GPS P(Y)码信号为例,其采用2 个十二级移位寄存器生成的P 码信号的自相关最大峰值比次大峰值高约30 dB[14]。 因此,对GPS 卫星P(Y)码信号的提纯度要达到至少30 dB。

2 波束形成方法

常用的波束形成器有常规波束形成器和MVDR 波束形成器。

常规波束形成器以归一化的阵列响应向量作为加权向量:

式中:as为阵列天线在数字波束主瓣指向方向的响应向量。

常规波束形成器计算简单且在各类波束形成器中稳健性最高,但是阵增益有限,无法满足卫星信号提纯对提高信号增益的需求。

MVDR 波束形成器也称为Capon 波束形成器,其原理是让感兴趣方向的信号无失真通过,同时约束波束输出噪声方差最小,可表述为

式中:Rx为M×M维的阵列天线接收信号协方差矩阵。

采用拉格朗日乘子法对上述问题进行求解,得到MVDR 波束形成器的加权向量为[15]

比较式(12)和式(7)可知,此时MVDR 波束形成器蜕化为常规波束形成器。

3 MVDR 波束形成器的提纯度分析

将阵列天线接收信号的协方差矩阵进行特征值分解为

式中:γmin为最小特征值。

将式(14)代入式(8)中可以得到

式中:pq(k)=aHsa(k) 为阵列流型向量匹配形成的静态波束响应;ρq,m=aHsum为阵列响应向量as和第m个特征向量间的相关性;peig,m(k)=uHma(k) 为特征向量um对权向量形成的特征波束响应。

由式(16)可以看出,MVDR 波束响应是常规静态波束响应和特征波束响应的叠加。 由于协方差矩阵的特征向量相互正交,因此特征波束之间也是相互正交的。 若需要在第m颗导航卫星方向k=km(m=1,2,…,D)形成零陷,则ρq,m通过调节特征波束peig,m(km)的大小,使得

从式(18)中可以看出,MVDR 波束在k=km方向的波束响应比常规静态波束的响应小20lg(γmin/γm)dB, 即零陷的深度与协方差矩阵的最小特征值γmin和第m个特征值的比值相关。 在干扰情况下,由于阵列接收到的卫星导航信号功率远小于热噪声功率,对接收数据协方差矩阵分解后得到的特征值基本都对应于热噪声,γm≈γmin,式(18)将简化为

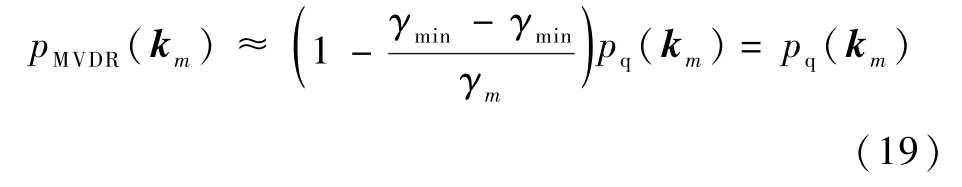
此时,MVDR 波束蜕化为常规静态波束,无法实现对卫星信号的有效提纯。

由式(19)的分析结果可知,若要在第m颗导航卫星方向k=km(m=1,2,…,D)形成零陷,则阵列协方差中km方向数据入射信号对应的特征值γm要远大于热噪声对应的特征值γmin。

4 波束形成器优化设计方法

为使MVDR 波束形成器输出信号中的目标卫星信号功率与非目标卫星信号功率满足式(6)的信号提纯度要求,本节提出一种数据协方差矩阵加载重构的优化波束设计方法,通过非目标导航卫星的方向信息和阵列布局构造“虚拟”干扰信号协方差矩阵,并加载到阵列接收数据协方差矩阵上,增大非目标卫星方向入射信号的特征值与热噪声特征值的比值,加深MVDR 波束在非目标卫星方向上的零陷深度响应。

令R′x,l为构造的用于计算主瓣指向第l颗卫星权向量值的数据协方差矩阵,可以写为

则依式(22)计算出的加权向量可使MVDR波束成形器输出信号满足式(6)的提纯度要求。

将计算步骤总结如下:

1) 根据式(10)计算阵列天线接收信号的协方差矩阵Rx。

2) 根据式(20)和式(21)并行计算D个协方差矩阵(R′x,1,R′x,2,…,R′x,D)。

3) 根据式(22)并行计算出主瓣分别指向D颗卫星的提纯波束加权向量(wMVDR(k1),wMVDR(k2),…,wMVDR(kD))。

4) 采用提纯波束加权向量根据式(5)对阵列天线接收信号进行提纯,并行输出提纯后的D颗卫星信号。

5 仿真分析

假设视野内存在10 颗导航卫星,卫星PRN 编号为1 ～10,导航信号载波频率为1 575.42 MHz,带宽为20.46 MHz,卫星信号到达接收阵列天线口面的功率电平为-125 dBm,系统热噪声功率电平为-100 dBm。 卫星相对于接收阵列天线坐标系0°方向的方位角及相对于水平面的仰角如

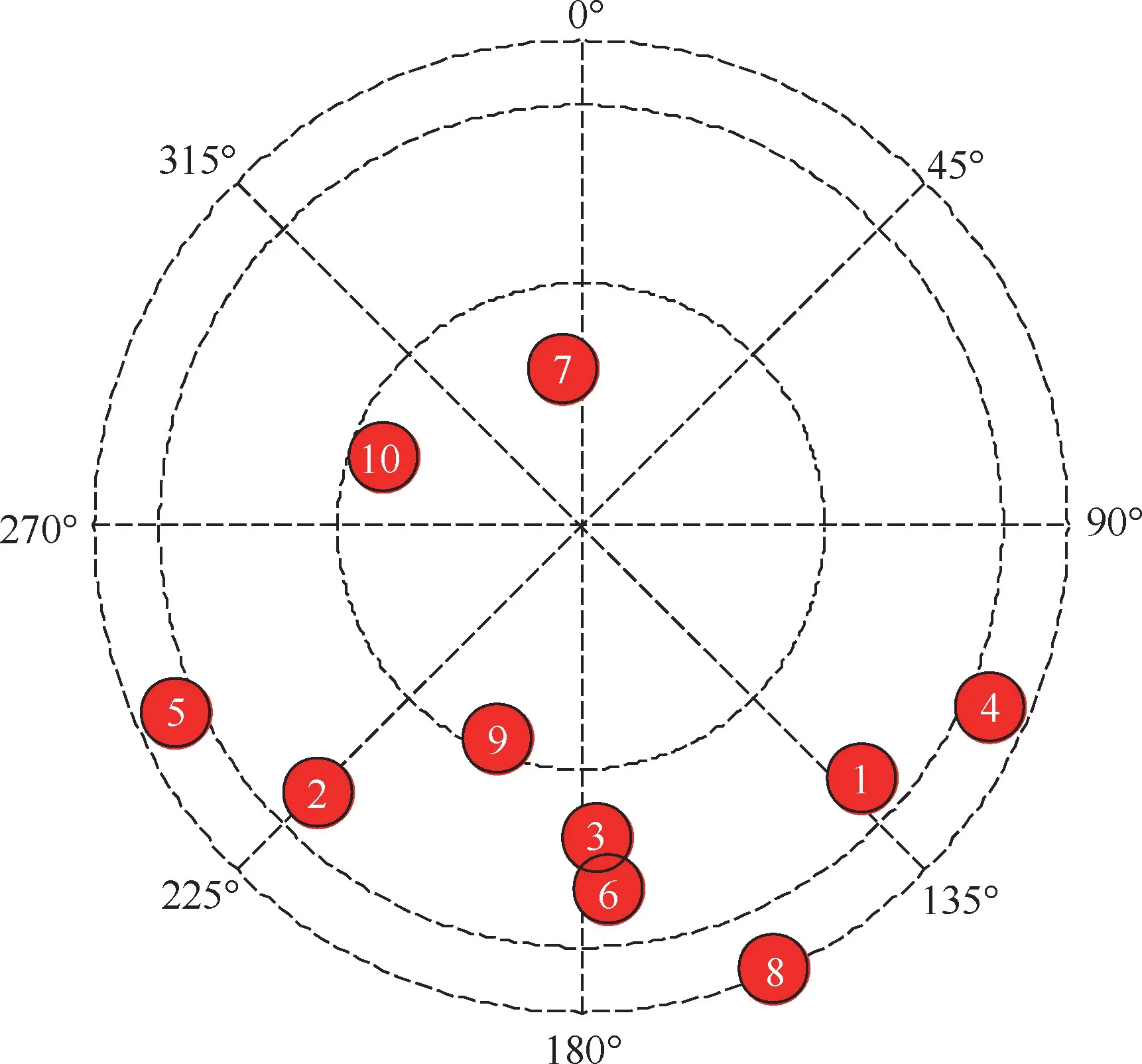
图2 卫星星座分布天顶俯视图Fig.2 Top view of satellite constellation distribution

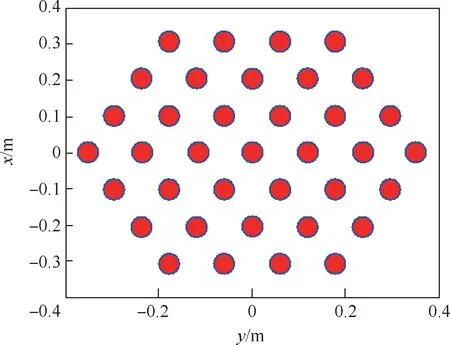
图3 接收阵列布局Fig.3 Receiving array layout

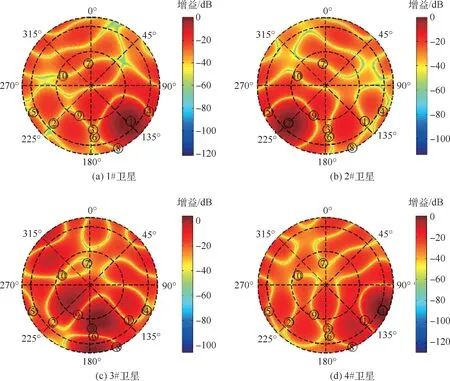
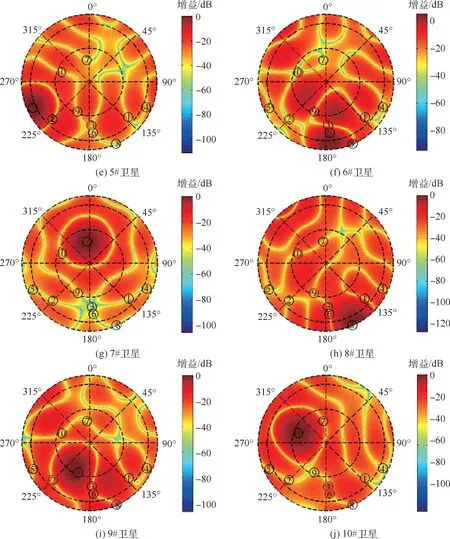
图4 优化波束响应Fig.4 Response of optimized beams

图5 为在1#卫星仰角(39.37°)上本文所提优化波束与常规波束在各方位上的波束响应。 从图5 中可以看出,优化波束和常规波束的波束宽度相当,且在1#卫星方向响应均为0 dB,可以使1#卫星播发的导航信号无失真通过。

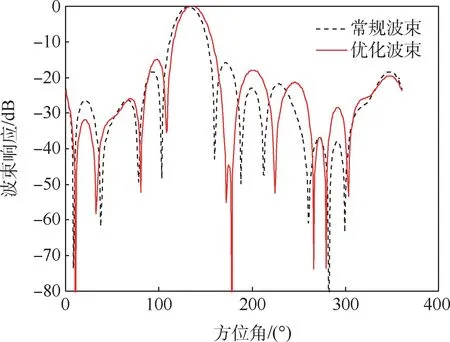
图5 1#卫星仰角上优化波束和常规波束响应对比Fig.5 Comparison of response of optimized beam and regular beams of satellite 1#

图6 为指向1#卫星的本文所提优化波束与常规波束在2# ～10#卫星仰角上各方向的波束响应对比。 从图6 中可以看出,常规波束在2# ～10#卫星入射方向的波束响应约为-20 dB 左右,对1#卫星的提纯度有限,而本文所提优化波束在2# ～10#卫星入射方向的响应超过-40 dB,可以有效抑制2# ～10#卫星信号。

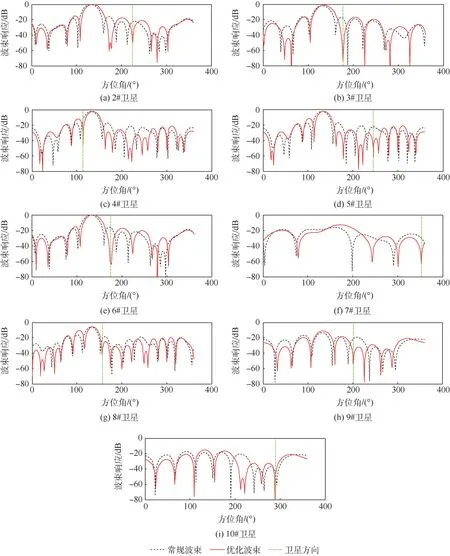
图6 1#波束在2# ～10#卫星方向的响应对比Fig.6 Comparison of responses of 1# beam in direction of 2# to 10# satellites

采用本文所提方法和常规波束形成方法同时生成指向10 颗卫星的分离提纯波束,图7 为10 个波束输出信号中各卫星信号成分的功率对比。 从图7 中可以看出,常规波束和本文所提优化波束对主瓣指向方向的卫星信号功率无损失,均保持在-125 dBm。 但是,对于指向3#卫星和6#卫星的常规波束,其波束输出信号中的6#卫星和3#卫星信号分量超过了提纯门限。 由表1 可知,3#卫星和6#卫星之间的方位差只有1.37°,根据文献[16]中的计算方法可以分别计算出在该阵列孔径条件下,常规波束形成器和本文所提波束形成器的方位分辨率分别为16.93°和0.92°,常规波束由于无法有效分辨3#卫星和6#卫星,通过常规波束提纯后,波束输出中临近方位的非目标卫星信号功率超过了提纯门限;而本文所提方法则可以有效分辨3#卫星和6#卫星,而通过本文所提方法提纯后,波束输出信号中非目标卫星信号的功率均低于提纯门限。

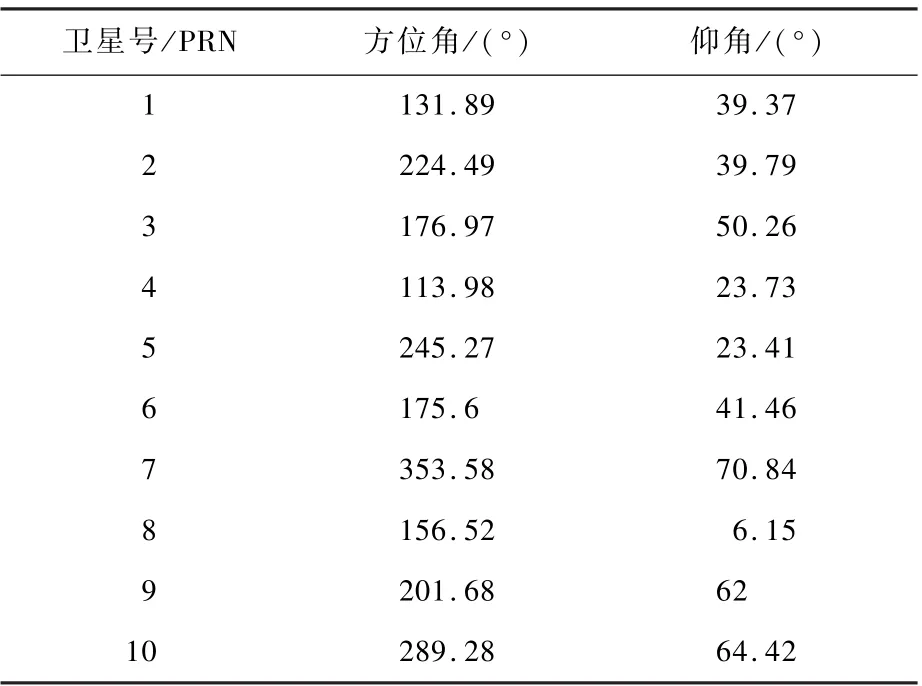
表1 导航卫星方位角和仰角Table 1 Azimuth and elevation of navigation satellites

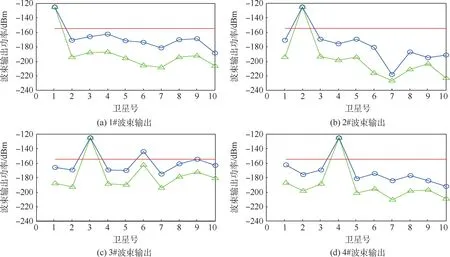
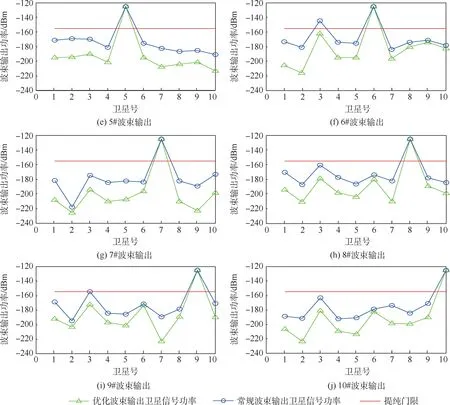
图7 1# ～10#波束输出中各卫星信号功率对比Fig.7 Comparison of satellite signal powers in 1# to 10# beam outputs

6 结 论

区别于现有的MVDR 波束形成方法,本文提出了一种数字波束优化设计方法,适用于转发式卫星导航欺骗干扰中的卫星导航信号提纯应用,总结如下:

1) 向阵列天线接收信号数据协方差矩阵上加载由非目标导航卫星的方向信息和阵列布局构造的“虚拟”干扰信号协方差矩阵,增大了非目标卫星方向入射信号的特征值与热噪声特征值的比值。

2) 提出了MVDR 波束形成器优化方法,使得波束指向方向的目标卫星信号被有效提纯。

3) 本文所提方法可以使得目标卫星信号从波束主瓣指向方向无失真通过,且非目标卫星信号受到波束旁瓣区域的零陷抑制,满足30 dB 的信号提纯度要求。