预应力混凝土梁下挠开裂后顶升过程刚度模拟方法研究
2022-11-08吴海军唐海淘陈涛罗春燕
吴海军, 唐海淘*, 陈涛, 罗春燕
(1.重庆交通大学 山区桥梁与隧道工程国家重点实验室, 重庆 南岸 400074; 2.重庆大学, 重庆市 400044; 3.重庆市酉阳第一中学校, 重庆市 409812)
预应力混凝土梁广泛应用在中国桥梁建设中,不乏出现预应力混凝土梁下挠后,需要顶升加固的案例。由于预应力混凝土开裂后的刚度降低,而且在主梁顶升过程中其裂缝逐渐闭合,刚度不断增大,如何准确模拟顶升过程中的刚度变化是制订顶升方案的关键问题。可以将其简单地视为主梁下挠开裂的逆过程,即顶升前刚度最小,随着顶升力的增加,挠度逐渐变小,裂缝逐渐闭合,刚度不断增加,当主梁下缘受压时,假定此时刚度完全恢复。
目前,对于开裂截面刚度计算的研究较多,主要分为变刚度和统一刚度两种方法。王磊等[1]通过对开裂后主梁的裂缝特征参数进行统计,将主梁划分为若干个开裂区段,分别求出每个开裂区段的有效刚度,形成阶梯刚度模式,再采用挠度分段积分的方法求出阶梯刚度下的荷载挠度;黄义涛等[2]通过假定未开裂段和纯弯段之间刚度按直线变化,计算变刚度梁的变形,试验数据证明该变刚度模型具有一定的适用性;杜进生等[3]基于无黏结部分预应力混凝土梁建立了使用荷载下开裂截面中性轴高度三次方程,得到相应截面的开裂截面惯性矩及有黏结非预应力钢筋的应力,而后利用JTJ 023—85《公路钢筋混凝土及预应力混凝土桥涵设计规范》计算无黏结部分预应力混凝土梁的挠度、裂缝宽度;胡志坚等[4]基于JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》,通过引入跨中弯矩修正系数的方法提出了具体的抗弯刚度修正公式。这些方法仅是针对某一裂缝状态下的刚度计算问题,而关于开裂截面梁顶升过程的变刚度计算的研究较少。该文基于有效惯性矩法,建立一种适合预应力混凝土梁顶升过程的刚度变化模型。
1 开裂截面顶升刚度变化模型的建立
1.1 开裂截面刚度退化模型
由于目前关于预应力混凝土梁顶升过程刚度变化的研究较少,鉴于主梁顶升是主梁下挠的逆过程,因此了解开裂截面的刚度退化规律非常必要。开裂截面刚度退化的提出主要是为了准确地计算挠度,尤其是对主梁开裂后的挠度计算。对于均质材料而言,当梁的截面形状、尺寸和材料已知时,梁的截面弯曲刚度是一个常数。而预应力混凝土梁是非均质的非弹性材料,因而在它受弯的全过程中,截面的弯曲刚度是变化的,其不仅随荷载增大而减小,而且还将随荷载作用时间的增长而减小。因此梁挠度的计算,要综合考虑不同荷载作用下的刚度以及沿梁长不同截面的刚度,提出一个合适的平均刚度,使之能够较准确地计算梁在各种状况下的变形。
对开裂前的挠度计算,各种公式没有太大的分歧。对开裂后混凝土构件的挠度计算,国内外学者进行了大量的研究,并提出了不少的挠度计算方法,主要有:刚度折减分析法、三折线法、直接双线性法、有效惯性矩法、刚度解析法和曲率积分法[5-10]。该文仅介绍有效惯性矩法。在荷载作用下梁开裂后,其裂缝之间总有一定的间隔未开裂,这些未开裂的截面对梁的总刚度是有影响的。因此,可认为梁的综合刚度是介于未开裂截面刚度与开裂截面刚度之间的某个数值,可以用等效惯性矩Ie来表示截面刚度。该方法最初由Branson[11-12]在 1965 年提出,他指出在某个开裂截面的有效惯性矩计算式为:
(1)
式中:m为待定系数;M为跨中截面弯矩;Mcr为截面开裂弯矩;Ig为未开裂截面惯性矩;Icr为开裂截面惯性矩。
1.2 基于有效惯性矩法开裂截面顶升过程刚度变化模型
1.2.1 有效惯性矩公式
由于顶升前无法确定裂缝完全闭合阶段,因此采用双直线法较为困难,而刚度解析法等过于复杂,最终选用有效惯性矩法来模拟顶升过程中主梁的刚度变化。通过不断代入跨中弯矩M实现刚度的变化。根据初始下挠模拟试算,待定系数m取1.0,其试算过程见后文。则有效惯性矩计算式如下:
(2)
式中:Icr为顶升前预应力混凝土梁跨中开裂截面惯性矩;跨中截面弯矩值M直接从有限元模型中提取;截面开裂弯矩Mcr根据JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[13]中6.5.2-3公式计算。计算公式如下:
Mcr=(σpc+γftk)W0
(3)

1.2.2 主梁刚度恢复判断准则
随着跨中挠度的减小,弯矩M值也相应减小,有效惯性矩增大,从而实现刚度在顶升过程中不断增大。主梁刚度恢复判断准则为:当弯矩M≤Mcr时,认为主梁裂缝完全闭合,刚度完全恢复。同时可通过比较有效惯性矩Ie与未开裂截面惯性矩Ig的大小关系验证其结果。
1.2.3 模型连续性处理方法
鉴于Midas/Civil软件不能在同一个模型实现惯性矩的动态变化,每个模型只能输入1个截面刚度,因此需采用多个模型共同实现模拟顶升主梁的全过程。这就必然导致前一个模型和后一个模型的下挠状态不一致,即后者挠度小于前者。但是,在忽略由于主梁变形引起的位移非线性的情况下,这个问题就不存在了。事实上在计算预应力混凝土梁的位移时通常没有考虑这种非线性,因此假设顶升位移与主梁下挠状态无关是合理的。
1.2.4 主梁刚度变化计算流程
利用跨中弯矩M的变化进而实现主梁刚度的递增,其计算流程见图1。
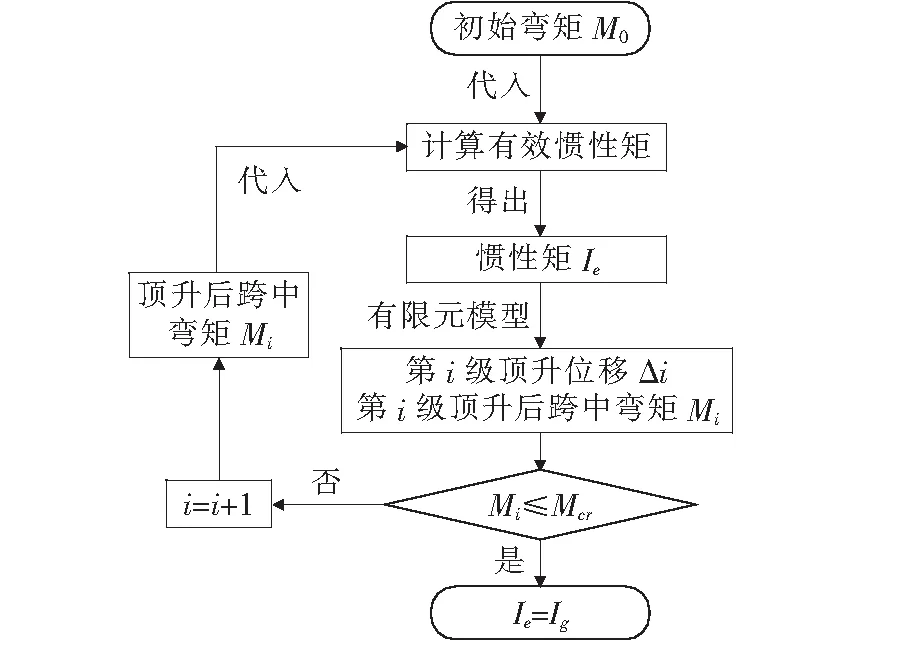
图1 主梁刚度计算流程图
2 应用实例
2.1 桥梁概况
稻城县香格里拉大桥,上跨赤土河。桥跨布置为(30+70+30) m三跨连续梁拱组合结构,桥面宽度为14.5 m。桥面行车道采用沥青混凝土铺装,桥面横坡为双向1.5%,桥面纵坡为-4.0%,横坡由梁顶形成,铺装等厚。主梁为预应力钢筋混凝土整体式箱梁结构,截面形式为单箱双室截面,材料为C40。采用两片拱肋,设置于人行道内侧,拱肋为钢管混凝土结构,采用等高度哑铃形截面,截面高度为1.8 m;拱肋计算跨度L=70.0 m,计算矢高f=17.5 m,矢跨比f/L=1/4,拱肋采用二次抛物线。两榀拱肋之间共设5道横撑,横撑均为“一”字形。“一”字形横撑主钢管截面为φ500 mm×10 mm,钢管内部不填充混凝土。全桥共设12组吊杆,均采用可置换式吊杆,纵桥向间距为5.0 m。桥梁布置图如图2所示。
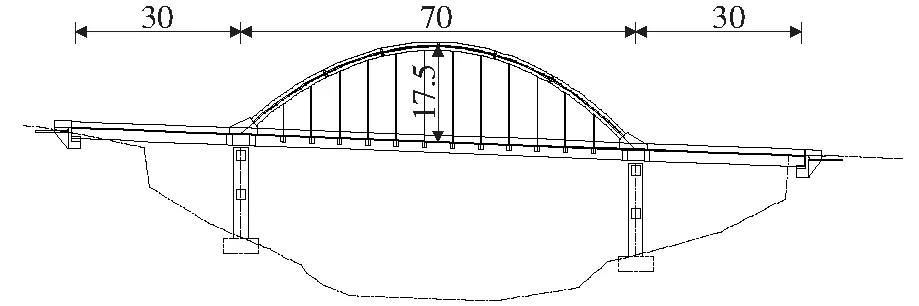
图2 桥梁布置图(单位:m)
2.2 工程背景
稻城县香格里拉大桥在施工期间由于吊杆安装前拆除了支架,导致主梁下挠,最大下挠值达到178 mm。顶升方案为:在现有钢管柱上方布置千斤顶,纵向布置8个顶位,每个顶位横向布置6个千斤顶,共48台千斤顶;考虑到主梁下挠现状,前期取20 mm为一级,后期逐渐过渡到10 mm、5 mm为一级,每顶升一级,需根据现场监测数据判定梁体受力状态是否合理,是否达到主梁设计标高,从而决策是否继续顶升,顶升过程需边顶升边支撑。顶升结束后,再张拉吊杆并增设其他加固措施。
2.3 有限元模型
应用Midas/Civil软件对该桥建立有限元计算模型,根据该桥的结构特点和施工工艺要求,在有限元建模中,主梁、主拱肋、肋间横撑均采用空间梁单元模拟,钢管混凝土采用联合截面法模拟,主梁与拱肋采用公共节点连接。结构离散后,全桥共有梁单元491个,节点469个。
3 实例分析
3.1 主梁下挠模拟及待定系数求取
准确模拟主梁的下挠是能否合理模拟主梁顶升过程的前提,模拟主梁下挠的关键在于Ie的取值,而Ie依赖于待定系数m以及初始跨中弯矩M0的取值,其中m可通过试算求得。由于依托工程为连续梁拱组合桥,为超静定结构,跨中区域梁体刚度的改变,导致位移协调方程发生变化,进而影响结构的受力,因此初始跨中弯矩M0也需要通过试算确定。对此该文解决思路为:首先,假设待定系数m以及跨中弯矩M0代入式(1)得到初始Ie;其次,通过有限元模型计算得到下挠模拟值Δ和跨中弯矩值M;最后,对比下挠模型值Δ与实测下挠值以及假定弯矩M0与计算弯矩M,判断两者是否接近,从而修正m、M0,如此循环,直到满足条件。经过试算,待定系数m取1.0,试算流程见图3,各下挠模拟参数值见表1。其中跨中未开裂截面惯性矩Ig以及开裂弯矩Mcr通过截面构造计算;开裂惯性矩Icr根据检测报告中关于跨中裂缝的描述进行估算,跨中区域裂缝最高为1.0 m。

图3 待定系数m、跨中弯矩M0试算流程图
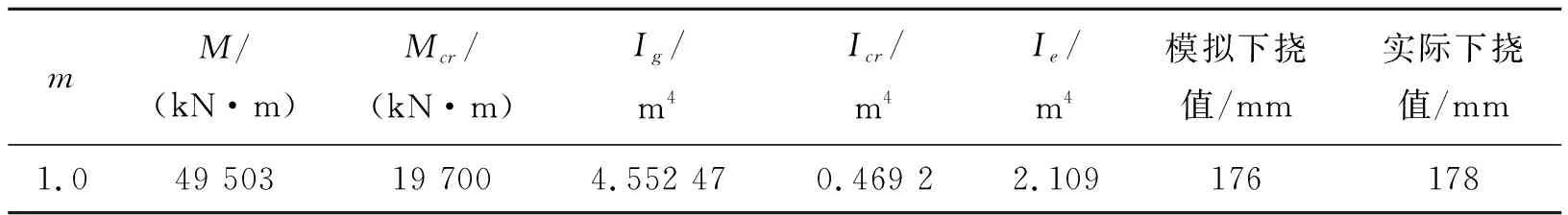
表1 主梁下挠模拟参数
3.2 刚度变化模拟
为减少工作量,有限元模型计算时,主梁顶升共分为8个阶段,前7阶段每阶段顶升20 mm,第8阶段顶升18 mm。其中每级的有效惯性矩Ie和每级所需顶升力见图4。顶升x高度的值代表从上一阶段顶升到x高度有限元模型采用的参数。

图4 各阶段顶升过程参数
由图4可以看出:随着顶升的进行,有效惯性矩呈非线性增长,前期有效惯性矩增长较慢,中期增长较快,主梁顶升到120 mm时,主梁刚度完全恢复。同时,单级顶升力同刚度变化情况符合较好,在前期每级顶升力偏大,但是中后期单级顶升力和刚度变化基本一致。这也从侧面验证了顶升力与有效惯性矩基本呈线性关系。
提取各阶段跨中弯矩值见图5。
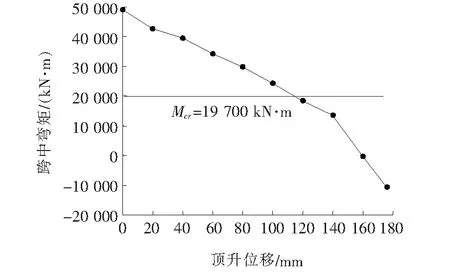
图5 各阶段跨中弯矩
由图5可得:① 随着顶升位移的增加,跨中弯矩逐渐减小,直接原因是顶升力的增加抵消了部分自重的影响;② 当顶升位移为115 mm时,跨中弯矩M小于开裂弯矩Mcr,此时近似认为主梁裂缝完全闭合,刚度完全恢复。当顶升位移超过140 mm时,由于主梁刚度在该阶段近似完全恢复,其弯矩下降幅度明显增加。
在实际顶升过程中,最终顶升位移为160 mm,所用顶升力为18 865 kN,对应计算顶升力为20 240 kN,较实际值偏大,偏差率为7%。实际顶升力、计算顶升力与最大顶升位移的关系见图6。从总体来看,顶升力与顶升位移关系的实际值和计算值符合情况较好。其中前期计算顶升力与实际顶升力差距较大,这是由于前期千斤顶的启动力对结果的影响较大,导致实际值偏大。后期计算顶升力与实际顶升力基本接近,且计算值普遍大于实际值,这可能是因为计算假设主梁裂缝闭合后主梁刚度完全恢复,但实际主梁刚度小于该值。
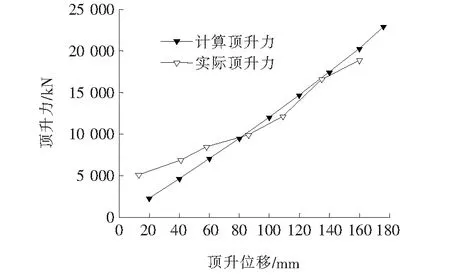
图6 顶升力与最大顶升位移关系
同时从图6可以明显看出顶升位移110 mm左右实力顶升力存在一个拐点,拐点前较为平缓,刚度较小,拐点后较陡,刚度较大。这与理论计算中通过跨中弯矩与开裂弯矩相对大小的判断结果基本相同。
选取跨中处5 m范围内宽度最大的两条横向裂缝进行监测,结果见表2。

表2 主梁跨中裂缝宽度变化
从表2可得:跨中横向裂缝闭合(裂缝宽度值不再变化)时,实际千斤顶力为12 370 kN,与之对应的实际顶升位移为110 mm,与通过刚度恢复判断准则预测的115 mm相差不大,进一步验证了该准则的有效性。
4 结论
(1) 基于Branson提出的有效惯性矩计算公式,提出了利用Midas/Civil软件模拟预应力混凝土梁下挠后顶升过程主梁刚度变化的方法。通过对比顶升力与顶升位移关系曲线的计算值与实际值,表明该方法可以较好地模拟混凝土梁顶升过程,且具有适用性。
(2) 通过主梁刚度恢复判断准则,合理预测了主梁刚度完全恢复(拐点)的位置,并通过顶升力与顶升位移关系曲线以及裂缝宽度发展两方面验证了该准则的有效性,进一步表明了该模拟方法具有适用性。
